Author: Denis Avetisyan
A new approach leveraging quantum entanglement offers the potential to dramatically reduce bandwidth demands in distributed storage systems.
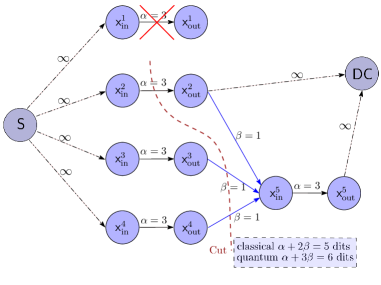
This review explores how quantum communication and entanglement-assisted codes can minimize both storage overhead and repair bandwidth, potentially surpassing the limitations of classical methods.
Traditional distributed storage systems face a fundamental tradeoff between storage capacity and communication bandwidth required for repair. This work, titled ‘Breaking the Storage-Bandwidth Tradeoff in Distributed Storage with Quantum Entanglement’, explores how leveraging quantum communication and entanglement among storage nodes can overcome this limitation. We demonstrate that, under specific conditions, it’s possible to simultaneously minimize both the storage overhead and the bandwidth needed to rebuild failed nodes-a feat impossible in classical systems. Could this quantum approach pave the way for dramatically more efficient and scalable data storage architectures?
Architecting Resilience: The Foundation of Distributed Storage
Contemporary data storage architectures are fundamentally shifting away from centralized models towards distributed systems, a necessity driven by the sheer volume and critical importance of digital information. These systems don’t store data on a single device, but rather fragment and replicate it across numerous interconnected nodes – servers, disks, or even geographically dispersed data centers. This distribution isn’t merely about capacity; it’s about building resilience. Should a single node fail – due to hardware malfunction, network interruption, or even a regional power outage – the data remains accessible and intact because copies exist elsewhere. This inherent redundancy drastically improves both availability – the percentage of time data is accessible – and durability – the long-term protection against data loss. The complexity of managing such distributed systems is considerable, but the gains in reliability and scalability are proving essential for applications ranging from cloud computing and financial transactions to scientific research and long-term archival storage.
The robustness of modern distributed storage hinges on a fundamental characteristic known as the Data Retrieval Property – the system’s inherent ability to flawlessly reconstruct lost or corrupted data even in the face of component failures. This isn’t simply about backup; it’s about actively rebuilding data on demand, leveraging redundancy techniques like erasure coding or replication. When a storage node falters, the system doesn’t report data loss; instead, it orchestrates a process of retrieval and recalculation, drawing upon the remaining healthy nodes to piece the missing information back together. This proactive approach ensures continuous data availability and durability, shielding users and applications from the disruptions inherent in large-scale, distributed infrastructure. The effectiveness of this property dictates the overall reliability and resilience of the entire storage system, making it a cornerstone of data management in the digital age.
Conventional data recovery strategies frequently employ ‘Single-Node Repair’, where a failed storage node is replaced by a single new node rebuilding the lost data. While conceptually straightforward and generally effective, this approach often encounters limitations stemming from network bandwidth. Reconstructing data from remaining nodes to a single replacement demands substantial data transfer, creating bottlenecks and prolonging the repair window. This extended downtime not only impacts system availability but also increases the probability of correlated failures – where another node fails during the recovery process, exacerbating data loss. Consequently, modern distributed storage systems are actively exploring alternative repair mechanisms, such as parallelized reconstruction or the use of erasure coding, to mitigate bandwidth constraints and dramatically reduce repair times, enhancing overall data resilience.
Beyond Classical Limits: Harnessing Quantum Communication for Repair
Quantum communication leverages principles of quantum mechanics, notably entanglement and superposition, to potentially surpass the capabilities of classical communication. Classical communication relies on bits representing 0 or 1, while quantum communication utilizes qubits, which can exist in a superposition of both states simultaneously. Entanglement, a specific quantum correlation, links two or more qubits such that the state of one instantaneously influences the others, regardless of distance. This allows for protocols, such as quantum key distribution, that offer provable security against eavesdropping, and theoretically enables data transmission paradigms not possible with classical systems. While practical implementation faces challenges related to decoherence and signal loss, these quantum phenomena provide the basis for exploring communication methods with enhanced capacity and security compared to traditional approaches.
Quantum Repair leverages the principles of quantum communication to improve the efficiency of data reconstruction following node failures in a distributed storage system. Traditional methods require retransmission of lost data segments, introducing latency proportional to the number of failed nodes. Quantum Repair schemes propose utilizing quantum phenomena, such as entanglement, to potentially transmit multiple data bits per quantum channel instance, reducing the total communication overhead. This approach aims to accelerate the recovery process, particularly in large-scale systems where node failures are more frequent and the cost of data reconstruction is significant. The effectiveness of Quantum Repair is contingent on overcoming practical limitations related to quantum channel capacity, decoherence, and the efficient implementation of quantum communication protocols.
Superdense coding is a quantum communication protocol that allows the transmission of two classical bits of information using only a single qubit. This is achieved by leveraging entanglement; an entangled pair of qubits is pre-shared between the sender and receiver. The sender, by performing one of four unitary operations on their qubit of the entangled pair, encodes two classical bits. The receiver, upon receiving the sender’s qubit, performs a Bell state measurement on the received qubit and their share of the entangled pair to decode the two classical bits. This effectively doubles the classical information capacity per qubit transmitted compared to direct transmission, potentially reducing bandwidth requirements in communication networks; however, this increase in efficiency does not circumvent the fundamental limits imposed by the \text{Holevo Bound} .
The Holevo bound represents a fundamental limit on the rate at which classical information can be reliably transmitted through a quantum channel. Specifically, it states that the quantum channel capacity, measured in bits per channel use, is upper-bounded by the minimum of the von Neumann entropy of the quantum state and the number of independent quantum dimensions used for encoding. This bound arises from the inherent probabilistic nature of quantum measurements; attempting to encode more classical information than allowed by the bound inevitably leads to increased error rates and ultimately, unreliable communication. The bound is expressed mathematically as C \le \min_p [I(X;Y)] , where C is the channel capacity, and I(X;Y) represents the mutual information between the classical input X and the quantum output Y. Consequently, even with techniques like superdense coding, the Holevo bound dictates the ultimate limits of data transmission rates achievable through quantum communication channels.
Optimizing Repair: Navigating the Constraints of Bandwidth and Storage
The storage-bandwidth tradeoff is a fundamental limitation in distributed storage systems. As the amount of data stored across a network increases – typically to improve fault tolerance and data availability – so too does the bandwidth required to repair data after failures. This relationship arises because greater storage capacity generally necessitates transferring more data during the repair process to reconstruct lost or corrupted information. Specifically, achieving higher levels of redundancy – by storing multiple copies or parity information – directly increases the volume of data that must be transmitted across the network when a storage node fails, thus creating a direct correlation between storage capacity and repair bandwidth requirements. Minimizing this tradeoff is a primary goal in the design of efficient distributed storage architectures.
The Cut-Set Bound, derived from graph theory, establishes a fundamental limit on the achievable rate of reliable communication within a distributed storage network. This bound operates by identifying ‘cut-sets’ – minimal sets of links whose removal disconnects the network – and calculating the capacity of these cuts. Specifically, the bound states that the rate of repair, or data reconstruction, is limited by the minimum capacity of any cut-set in the network’s topology. Mathematically, this is expressed as the minimum number of links that must be severed to partition the storage nodes, directly impacting the bandwidth required for data recovery after a node failure. Therefore, the Cut-Set Bound serves as a theoretical lower limit on the repair bandwidth, independent of the specific encoding scheme used, and dictates the minimum resources necessary to maintain data availability and reliability.
Efficient information encoding is paramount in quantum distributed storage systems because it directly impacts the rate at which data can be transmitted across quantum communication channels. Unlike classical systems where bits represent information, quantum systems utilize qubits, potentially allowing for greater information density. Maximizing the data transferred per qubit – achieved through optimized encoding schemes – reduces the total number of qubits required for data repair. This reduction in qubit transmission translates directly to lower repair overhead, minimizing both bandwidth consumption and the associated resources needed for successful data reconstruction following node failures. Effective encoding strategies must also account for the inherent limitations of quantum channels, such as decoherence and transmission loss, to maintain data integrity and ensure reliable repair operations.
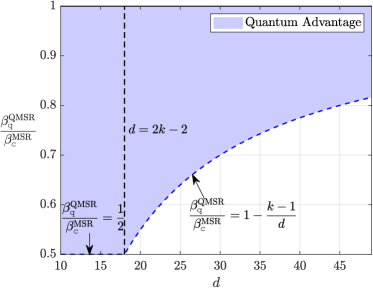
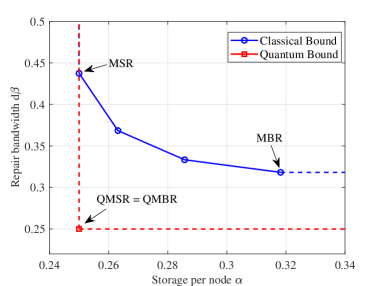
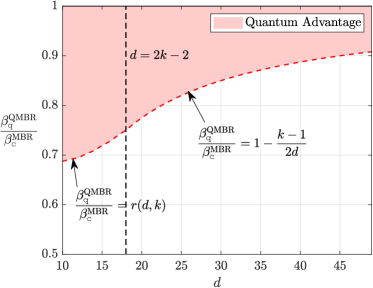
Entanglement-assisted repair strategies offer quantifiable advantages over classical approaches to data recovery in distributed storage systems. Specifically, results indicate a reduction in required repair bandwidth by a factor of two when operating at the minimum storage regeneration (MSR) point, provided the number of failed nodes, d, is less than or equal to 2k-2, where k represents the redundancy level. Furthermore, this method introduces a novel operating point characterized by the simultaneous minimization of both repair bandwidth and per-node storage requirements; this feature is not achievable using traditional, classical repair schemes.
Quantum State Representation and Repair Protocols: A New Paradigm for Resilience
Accurate representation of quantum states presents a unique challenge, as these states exist not as definite values but as probabilities. To address this, physicists employ the ‘Density Matrix’, a mathematical construct that moves beyond the limitations of wave functions when dealing with mixed states – those representing statistical ensembles of quantum systems. Unlike a wave function which describes a single, known quantum state, the density matrix ρ provides a complete description of a quantum state, regardless of whether it is pure or mixed, by capturing all statistical properties of the quantum information. This is crucial because real-world quantum systems are often subject to noise and decoherence, leading to mixed states where the precise quantum state is unknown. The density matrix, therefore, isn’t simply a theoretical tool, but a necessity for modeling and manipulating quantum information in practical scenarios, allowing for the calculation of observable quantities and the development of robust quantum technologies.
Quantum repair offers a potentially revolutionary approach to data reconstruction, capitalizing on the unique properties of entanglement to surpass the limitations of classical methods. While classical data recovery relies on redundant copies and is constrained by bandwidth requirements, quantum repair utilizes entangled quantum states to distribute information in a way that allows for faster and more efficient reconstruction, even when portions of the data are lost or corrupted. This is achieved because entangled particles exhibit correlations that transcend classical physics, enabling the recovery of information from a smaller amount of transmitted data. The potential speedup arises from the ability to encode information in superpositions and leverage the inherent parallelism of quantum mechanics, ultimately reducing the communication overhead needed for reliable data storage and retrieval.
Analysis reveals a substantial advantage in bandwidth efficiency when employing quantum Minimum Storage Regeneration (QMSR) over its classical counterpart, Minimum Storage Regeneration (MSR). The research demonstrates that the ratio of bandwidth required by QMSR to MSR is precisely 3/4 when the redundancy level, denoted as d, is greater than or equal to 2k-2, where k represents the number of storage nodes. Notably, when d is less than 2k-2, this ratio improves to 1/2, indicating a further reduction in bandwidth usage. These findings highlight the potential for quantum communication strategies to significantly optimize data storage and reconstruction processes, particularly in scenarios where bandwidth is a limiting resource, and offer a quantifiable measure of improvement over traditional classical methods.
Effective quantum data repair isn’t simply about leveraging the advantages of quantum communication; it demands a careful negotiation with fundamental limits and engineering realities. While quantum entanglement offers the potential for faster reconstruction of lost information, the Holevo bound-a theorem dictating the maximum information capacity of a quantum channel-constrains how much information can be reliably transmitted. Consequently, optimizing repair protocols requires a delicate balance: maximizing the benefits of quantum communication to minimize repair bandwidth, while remaining within the bounds set by the Holevo theorem and acknowledging the practical difficulties inherent in building and maintaining stable quantum channels. This necessitates strategies that consider not only theoretical gains but also the feasibility of implementation, factoring in issues like decoherence, error correction, and the overhead associated with creating and distributing entangled states.
The pursuit of efficient distributed storage, as detailed in this work, hinges on a holistic understanding of system interactions. It’s not merely about optimizing individual components, but recognizing how they collectively influence performance. This echoes Robert Tarjan’s observation: “If a design feels clever, it’s probably fragile.” The paper’s exploration of quantum entanglement to bypass the storage-bandwidth tradeoff isn’t a ‘clever’ trick to circumvent fundamental limits; rather, it’s an attempt to fundamentally restructure the system. By intelligently leveraging quantum properties, the research strives for an inherently robust design-one where minimized storage and repair bandwidth aren’t achieved through complex workarounds, but through elegant, systemic principles. The focus on minimizing both storage and repair bandwidth simultaneously demonstrates a commitment to overall system health, aligning with the principle that structure dictates behavior.
Where Do We Go From Here?
The pursuit of efficient distributed storage perpetually reveals itself as a game of elegant compromises. This work, by suggesting a path beyond the conventional storage-bandwidth tradeoff through quantum entanglement, does not dissolve the inherent limitations – it merely relocates them. The cost of entanglement generation and maintenance, currently substantial, remains a practical barrier. Future investigations must rigorously assess the energy overhead and decoherence rates as system scale increases; a marginal reduction in bandwidth is cold comfort if it demands an unsustainable energy budget.
Furthermore, the assumption of a fully connected quantum network, while theoretically appealing, feels distinctly optimistic. Real-world deployments will necessitate navigating noisy channels and imperfect entanglement distribution. Consequently, research should prioritize developing robust quantum error correction strategies specifically tailored to the demands of large-scale distributed storage, and explore the viability of hybrid quantum-classical approaches that leverage the strengths of both paradigms.
Perhaps the most intriguing avenue lies in reconsidering the very notion of ‘repair’. The current framework, predicated on reconstructing lost data, may not be the most efficient strategy in a quantum context. Could entanglement facilitate a form of ‘quantum state transfer’ that bypasses reconstruction altogether? Such a shift in perspective, however radical, may ultimately reveal a more fundamental pathway to minimizing both storage and bandwidth costs, provided one is willing to accept the inevitable trade-offs inherent in any beautifully complex system.
Original article: https://arxiv.org/pdf/2601.10676.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- The Winter Floating Festival Event Puzzles In DDV
- Jujutsu Kaisen Modulo Chapter 18 Preview: Rika And Tsurugi’s Full Power
- Upload Labs: Beginner Tips & Tricks
- Best Video Game Masterpieces Of The 2000s
- Top 8 UFC 5 Perks Every Fighter Should Use
- How To Load & Use The Prototype In Pathologic 3
- How to Increase Corrosion Resistance in StarRupture
- USD COP PREDICTION
- Jujutsu: Zero Codes (December 2025)
- Roblox 1 Step = $1 Codes
2026-01-16 09:14