Author: Denis Avetisyan
A new approach combines coded computation and learning-based techniques to dramatically improve the efficiency of perfectly secure distributed matrix multiplication.
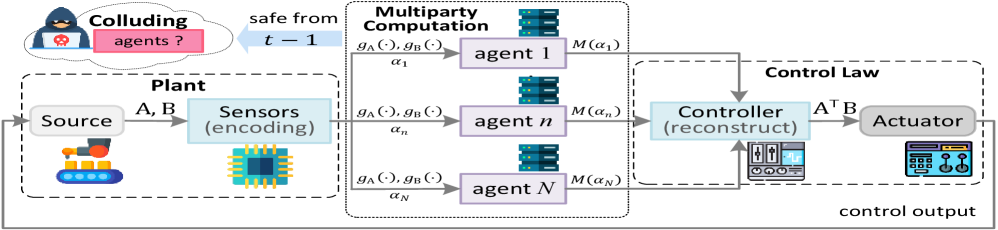
This work presents a framework for privacy-preserving collaborative computation that reduces communication and computational costs while guaranteeing information-theoretic security through low-rank tensor decomposition.
Achieving both rigorous privacy and computational efficiency remains a central challenge in distributed machine learning. This is addressed in ‘Learning-Augmented Perfectly Secure Collaborative Matrix Multiplication’, which introduces a novel framework for secure multiparty computation of matrix multiplication. By integrating coded computation with tensor-decomposition-based optimization, the proposed scheme guarantees information-theoretic privacy while demonstrably reducing communication and computational costs-achieving up to 80% gains in scalability. Could this approach unlock practical, privacy-preserving solutions for large-scale collaborative data analysis?
The Fragility of Privacy in Modern Computation
Conventional computational models frequently necessitate the delegation of data processing to a centralized entity, creating inherent vulnerabilities regarding data privacy. This reliance on a single point of control poses significant risks; sensitive information must be entrusted to a potentially compromised or malicious party, opening avenues for data breaches and misuse. Consider, for instance, financial transactions, medical record analysis, or even personalized advertising – each typically involves sharing private data with a central server. This established paradigm fundamentally conflicts with growing demands for data sovereignty and individual privacy, prompting the need for alternative computational frameworks where data remains distributed and protected even during processing. The implications extend beyond individual privacy, impacting competitive advantage for businesses and national security concerns as data becomes increasingly valuable.
Secure Multiparty Computation (SMC) presents a compelling approach to privacy-preserving data analysis, enabling multiple parties to jointly compute a function on their private inputs without revealing those inputs to each other. However, realizing this potential faces significant hurdles; current SMC protocols often demand computational resources that scale dramatically with the number of parties or the complexity of the function being computed. This exponential growth in processing requirements – frequently involving intensive cryptographic operations – renders many existing methods impractical for real-world applications involving large datasets or numerous participants. Consequently, a substantial research effort focuses on developing more efficient SMC protocols that minimize computational overhead while maintaining rigorous security guarantees, aiming to bridge the gap between theoretical possibility and practical deployment.
The pursuit of secure computation continually encounters a critical tension: the desire for unassailable privacy often clashes with the demands of practical efficiency. Current cryptographic protocols capable of safeguarding data during computation frequently rely on complex mathematical operations, leading to substantial computational overhead and rendering them impractical for large datasets or real-time applications. Researchers are actively exploring innovative techniques – including homomorphic encryption, secret sharing schemes, and garbled circuits – to minimize this performance penalty without compromising security. The challenge lies not simply in creating secure systems, but in engineering solutions that balance robust privacy guarantees with the computational resources available in real-world scenarios, ultimately determining the feasibility of widespread adoption and application of these powerful cryptographic tools.
Foundations of Privacy: Perfectly Secure Matrix Multiplication
Perfectly Secure Matrix Multiplication (PSMM) is a cryptographic protocol designed to compute the product of matrices without revealing any information about the input matrices themselves to any party involved in the computation. This is achieved by constructing a secure multi-party computation (MPC) where each input matrix is shared among multiple parties, and the computation proceeds without any single party having access to the complete input data. The result, C = A \times B, is revealed, but the individual elements of matrices A and B remain confidential. PSMM guarantees perfect privacy, meaning no information about the inputs is leaked, even to an adversary controlling a significant portion of the computing parties, provided the protocol is correctly implemented and the underlying cryptographic assumptions hold.
Perfectly Secure Matrix Multiplication (PSMM) employs Polynomial Sharing to decompose matrix elements into polynomial shares, distributing data across multiple parties such that no single party learns the original value. Each party holds one share, and collectively, they can reconstruct the original data for computation. To further obscure individual values during the multiplication process, PSMM utilizes Beaver’s Triple – a set of three random values (a, b, c) where c = a \cdot b – allowing parties to compute products without revealing their inputs. One party holds a, another b, and a third holds the pre-shared product c, enabling a secure dot product calculation. These techniques, combined, ensure that no information about the original matrix elements is leaked during the multiplication process, preserving perfect privacy.
Finite fields, denoted as GF(q) where q is a prime power, are fundamental to Perfectly Secure Matrix Multiplication (PSMM) because they provide the algebraic structure necessary for secure computation. Operations within a finite field – addition, subtraction, multiplication, and importantly, division – are well-defined and prevent intermediate values from expanding to unbounded sizes, which could reveal information about the original data. The properties of finite fields ensure that all computations remain within a bounded range, mitigating potential side-channel attacks and guaranteeing the correctness of cryptographic protocols like Beaver’s Triple generation and Polynomial Sharing. Specifically, calculations are performed modulo a large prime number chosen to be larger than any input value, effectively wrapping values and preventing information leakage through magnitude.
Perfectly Secure Matrix Multiplication (PSMM), while providing strong privacy guarantees, introduces significant computational overhead due to the cryptographic operations required for secure computation. The complexity scales rapidly with matrix dimensions, primarily stemming from the need for extensive masking and sharing of data, along with the arithmetic operations performed over finite fields. Consequently, research is actively focused on optimization techniques such as reducing the number of cryptographic operations, employing more efficient finite field implementations, and exploring parallelization strategies to mitigate this complexity and make PSMM practical for larger-scale applications. These efforts aim to balance the desired level of security with acceptable computational costs.
Harnessing Dimensionality Reduction for Efficiency
Low-rank decomposition is a matrix factorization technique that approximates a given matrix with a lower-rank matrix, thereby reducing computational complexity. This approach is conceptually similar to Strassen’s algorithm, which reduces the number of multiplications required for matrix multiplication from O(n^3) to approximately O(n^{2.81}) . By representing a matrix A as the product of two smaller matrices, U and V , where A ≈ UV and the rank of UV is significantly lower than the rank of A , subsequent operations involving A can be performed on these smaller matrices, leading to reduced memory usage and faster computation times. This is particularly effective when the original matrix contains significant redundancy or near-linear dependence among its rows or columns.
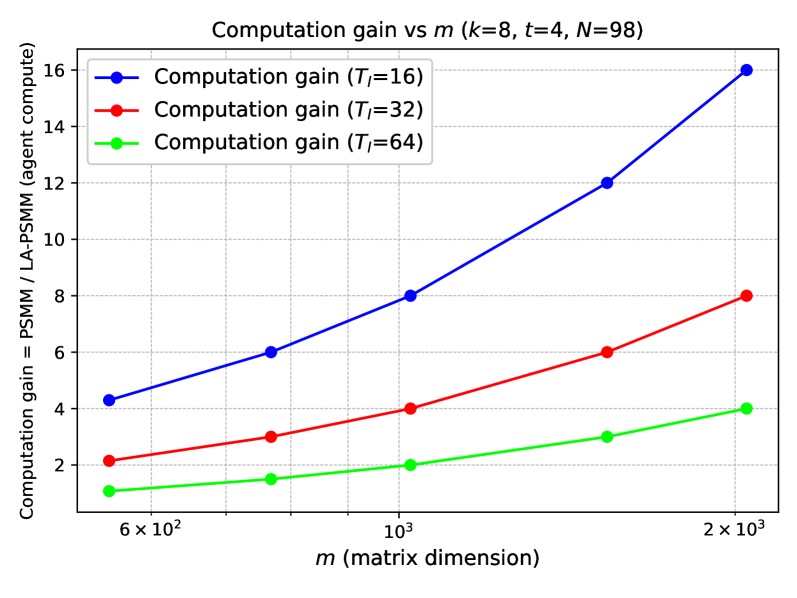
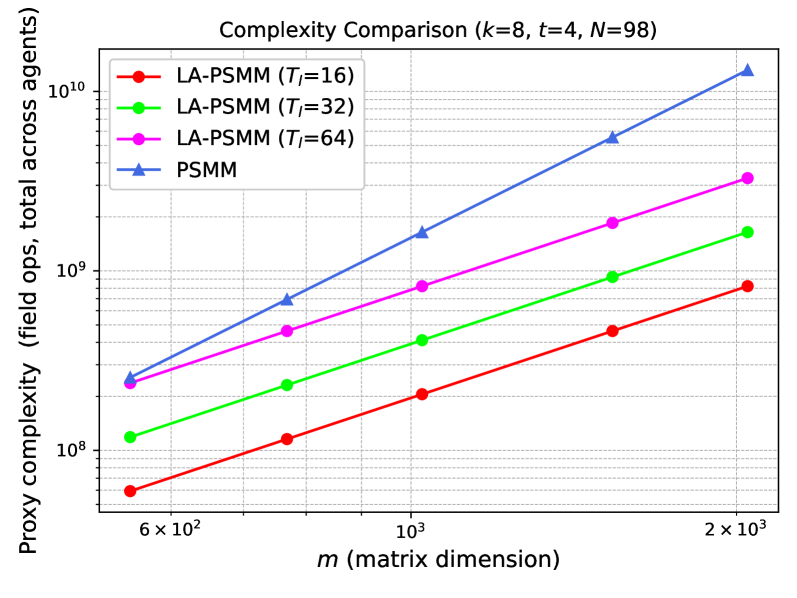
Applying low-rank decomposition to the Product Sum Matrix Multiplication (PSMM) operation yields substantial computational savings by approximating high-rank matrices with lower-rank counterparts. This reduction in complexity stems from decreasing the number of arithmetic operations required; instead of performing calculations on matrices of dimension n \times n, the decomposed matrices operate on smaller dimensions, effectively changing the computational cost from O(n^3) to a lower polynomial order dependent on the chosen rank. Consequently, PSMM, which frequently appears in various scientific computing tasks like density functional theory and machine learning, becomes tractable for larger problem sizes that were previously computationally prohibitive, thereby enabling practical applications in fields requiring high-dimensional matrix computations.
Numerical results, detailed in Figures 4 and 5, demonstrate a clear correlation between problem size and computational efficiency gains achieved through the application of low-rank decomposition to Parametric Sparse Matrix Multiplication (PSMM). As the dimensions of the matrices increase – specifically, as the number of non-zero elements grows – the computational cost associated with standard PSMM operations rises significantly. However, the use of low-rank approximations demonstrably mitigates this increase. The figures illustrate that while the computational cost continues to grow with problem size when using low-rank decomposition, the rate of growth is substantially reduced compared to standard PSMM, indicating a clear scaling advantage for larger problem instances. This effect is observed across multiple test cases and matrix structures, confirming the scalability benefits of the technique.
While low-rank decomposition aims to reduce computational cost, determining the optimal low-rank approximation introduces its own computational challenges. Algorithms such as the Singular Value Decomposition (SVD) – commonly used to compute a low-rank approximation – exhibit a time complexity of O(min(m2n, mn2)) for an m \times n matrix. For very large matrices, this calculation can become prohibitively expensive, potentially exceeding the savings gained from simplifying subsequent matrix operations. Consequently, research focuses on developing efficient, approximate methods – like randomized SVD or adaptive cross-approximation – to balance the cost of finding a low-rank approximation with the overall reduction in computational burden.
LA-PSMM: A Paradigm Shift in Secure Computation
Learning-Augmented Perfectly Secure Matrix Multiplication, or LA-PSMM, represents a significant advancement in secure multi-party computation by intelligently merging the robust privacy of Perfectly Secure Matrix Multiplication (PSMM) with the efficiency gains of machine learning. Traditionally, PSMM, while guaranteeing complete data confidentiality, has been computationally expensive, hindering its practical application. LA-PSMM addresses this limitation by leveraging machine learning algorithms to optimize the underlying matrix operations. Specifically, the approach employs a reinforcement learning agent to discover efficient, low-rank approximations of the matrices involved, drastically reducing the computational burden without compromising the fundamental privacy guarantees. This synthesis allows for secure computations on larger datasets and more complex models than previously feasible, opening new avenues for privacy-preserving data analysis and collaborative computation.
The computational efficiency of secure multiparty computation hinges on minimizing operations, and recent advancements leverage the power of machine learning to achieve this. Researchers employed AlphaTensor, a reinforcement learning agent, to explore and identify efficient low-rank decompositions of matrices central to secure computation protocols. This agent, trained through iterative self-play, discovers approximations that significantly reduce the computational burden without compromising security. By skillfully finding lower-dimensional representations of these matrices, AlphaTensor optimizes performance-essentially, it learns to perform complex calculations with fewer steps. This approach allows for faster and more scalable secure computations, paving the way for practical applications requiring privacy-preserving data analysis and collaborative problem-solving.
Learning-Augmented Perfectly Secure Matrix Multiplication (LA-PSMM) represents a significant advancement in secure computation by preserving the stringent privacy protections of Perfectly Secure Matrix Multiplication (PSMM) while substantially decreasing computational demands. Traditional methods of secure computation often incur substantial overhead, limiting their practical application; however, LA-PSMM leverages machine learning to optimize the underlying matrix operations. This optimization doesn’t compromise security-the system retains the mathematical guarantees ensuring no information leakage-but instead, efficiently restructures the computation. By discovering low-rank approximations through a reinforcement learning agent, the system reduces the complexity of matrix multiplications, enabling faster processing and broader applicability of privacy-preserving data analysis. The result is a pathway toward deploying secure multi-party computation in resource-constrained environments without sacrificing confidentiality.
A significant advancement in scalable secure computation lies in the reduced agent count for decoding within the Learning-Augmented Perfectly Secure Matrix Multiplication (LA-PSMM) framework. Traditional methods often require k^2 agents for this process, a number that quickly becomes prohibitive as the scale of computation increases. LA-PSMM, however, leverages machine learning to achieve a reduction to just s agents when s < k^2, dramatically improving scalability. This agent count is further mathematically bounded by N ≤ min{2k^2 + 2t - 3, k^2 + kt + t - 2}, demonstrating a potentially substantial advantage over established techniques like the BGW job-splitting method, which necessitates k^2(2t-1) agents for comparable operations. This optimization not only accelerates secure computations but also opens doors to tackling larger, more complex datasets while preserving perfect privacy.
The pursuit of perfectly secure collaborative matrix multiplication, as detailed in this work, demonstrates a compelling need for holistic system design. The paper’s innovative combination of coded computation and learning-based optimization isn’t merely a technical advancement; it’s an acknowledgement that efficiency and security are inextricably linked within the broader architecture. As Edsger W. Dijkstra stated, “It’s always possible to complicate things, but it’s much more difficult to simplify them.” This principle resonates deeply with the approach taken here, where reducing communication and computational costs isn’t achieved through added complexity, but through elegant, streamlined integration of existing techniques, ultimately realizing information-theoretic privacy.
What Lies Ahead?
This work offers a compelling demonstration of how learning-based optimization can be harnessed within the rigorous framework of coded computation. However, the question remains: what are the true boundaries of this synergy? The current approach, while effective for matrix multiplication, implicitly optimizes for reductions in communication and computation. A more fundamental inquiry is needed to determine whether these are, in fact, the correct metrics for progress in privacy-preserving machine learning. Is minimizing these costs simply a local optimum, obscuring more efficient, albeit less intuitive, algorithmic structures?
The reliance on low-rank tensor decomposition introduces a predictable constraint. While it simplifies the problem, it begs the question of how to extend this framework to handle higher-rank, or even full-rank, matrices without incurring prohibitive costs. The path forward likely involves a deeper exploration of alternative decomposition techniques, or perhaps a shift towards computation schemes that bypass decomposition altogether. Simplicity is not minimalism; it is the discipline of distinguishing the essential from the accidental, and this distinction is rarely obvious.
Ultimately, the true test will lie in scaling these techniques beyond the idealized settings of current research. The complexities of real-world distributed systems-noisy channels, heterogeneous computing resources, and adversarial participants-will undoubtedly expose unforeseen vulnerabilities and limitations. Addressing these practical challenges will require a holistic approach, recognizing that a secure computation scheme is not merely an algorithm, but an ecosystem-and the behavior of an ecosystem is dictated by its structure.
Original article: https://arxiv.org/pdf/2601.09916.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- Jujutsu Kaisen Modulo Chapter 18 Preview: Rika And Tsurugi’s Full Power
- How to Unlock the Mines in Cookie Run: Kingdom
- ALGS Championship 2026—Teams, Schedule, and Where to Watch
- Upload Labs: Beginner Tips & Tricks
- Top 8 UFC 5 Perks Every Fighter Should Use
- Jujutsu: Zero Codes (December 2025)
- How to Unlock & Visit Town Square in Cookie Run: Kingdom
- Roblox 1 Step = $1 Codes
- Mario’s Voice Actor Debunks ‘Weird Online Narrative’ About Nintendo Directs
- The Winter Floating Festival Event Puzzles In DDV
2026-01-17 22:11