Taming QCD: Improving Precision in Hadronic Tau Decay Analysis

Author: Denis Avetisyan

Researchers are leveraging advanced mathematical techniques to refine calculations of hadronic tau decays, a crucial process for pinpointing the strength of the strong force.

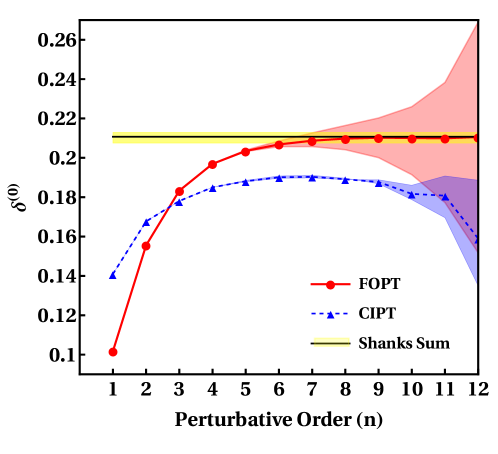
The study precisely determines <span class="katex-eq" data-katex-display="false">\delta(0)</span> within Quantum Chromodynamics (QCD) through higher-order coefficient analysis, demonstrating that perturbative expansions-with uncertainties represented by shaded regions-converge towards a mean value-defined by the Shanks sum-while variations across different resummation techniques, visualized as yellow bands, quantify the inherent spread around this central prediction, all calculated using <span class="katex-eq" data-katex-display="false">\alpha_s = 0.31959</span>. — The study precisely determines $\delta(0)$ within Quantum Chromodynamics (QCD) through higher-order coefficient analysis, demonstrating that perturbative expansions-with uncertainties represented by shaded regions-converge towards a mean value-defined by the Shanks sum-while variations across different resummation techniques, visualized as yellow bands, quantify the inherent spread around this central prediction, all calculated using $\alpha_s = 0.31959$ .

This review explores the application of sequence transformations, including the Shanks transformation, to enhance the convergence of perturbative QCD series in hadronic tau decays and improve the determination of the strong coupling constant.

Precise determination of the strong coupling constant relies on accurately modeling perturbative corrections in quantum chromodynamics, yet conventional fixed-order calculations become increasingly challenging at higher orders. This paper, ‘Hadronic tau decays at higher orders in QCD’, explores an alternative approach by employing nonlinear sequence transformations-specifically the Shanks transformation and Wynn’s ε-algorithm-to extrapolate information from lower-order perturbative expansions of hadronic τ decays. The analysis successfully estimates several higher-order coefficients, offering a systematic method for probing perturbative effects without explicit multi-loop calculations. Could these techniques provide a viable pathway towards improved precision in determining fundamental parameters of the Standard Model?

The Precise Window into Quantum Chromodynamics

Hadronic tau decays represent a crucial window into the strong force, serving as a primary method for precisely determining the strong coupling constant, $\alpha_s$ . This reliance stems from the unique properties of the tau lepton, which decays via the weak interaction into hadrons with a well-defined energy. By meticulously analyzing the distribution of these decay products, physicists can indirectly probe the intricacies of Quantum Chromodynamics (QCD), the theory governing the strong interaction. Unlike direct measurements of $\alpha_s$ which are often model-dependent, hadronic tau decays offer a theoretically clean pathway, allowing for non-perturbative effects to be systematically addressed and constrained. Consequently, continued refinement of analyses involving these decays is vital for pushing the boundaries of precision in QCD and furthering understanding of the fundamental forces of nature.

The calculation of physical quantities within the Standard Model often relies on perturbation theory, yet its application to strong interactions presents unique difficulties. Traditional fixed-order perturbation theory, while successful in quantum electrodynamics, exhibits notably slow convergence when applied to hadronic tau decays. This sluggish convergence arises from the nature of the strong force, where interactions are not easily described by a small parameter, leading to infinite series requiring an impractical number of terms for accurate results. Furthermore, predictions derived from this approach display a pronounced dependence on the arbitrary energy scale chosen for calculations; altering this scale significantly impacts the final result, introducing substantial theoretical uncertainty. Consequently, obtaining precise determinations of parameters like the strong coupling constant $\alpha_s$ requires innovative techniques that mitigate these challenges and reduce scale dependence, pushing beyond the limitations of conventional perturbative expansions.

Determining the $\delta(0)$ correction – a crucial component in precisely calculating the strong coupling constant via hadronic tau decays – presents significant analytical challenges. This leading order correction isn’t a straightforward calculation; it demands meticulous attention to the perturbative coefficients that arise from quantum chromodynamics. These coefficients, representing the strength of interactions, require careful expansion and renormalization to eliminate infinities and ensure physically meaningful results. Furthermore, the calculation involves complex integrals over the full range of possible hadronic states, necessitating sophisticated techniques to achieve accurate numerical evaluation and control systematic uncertainties. Successfully extracting $\delta(0)$ therefore hinges on a robust framework for managing both the theoretical complexity of the perturbative series and the computational demands of the integral calculations.

Finite Energy Sum Rules represent a sophisticated, non-perturbative approach to understanding hadronic tau decays, yet their practical application presents significant hurdles. The method relies on analytically continuing dispersion integrals into the complex plane, a process demanding careful consideration of integration contours and the handling of potential singularities. Computationally, these rules involve evaluating multi-dimensional integrals and solving complex equations, placing a substantial burden on available resources. Moreover, the accuracy of results is intrinsically linked to the approximations employed in modeling the high-energy behavior of the integrand – typically involving truncation of operator product expansion terms. Subtle changes in these approximations can introduce systematic uncertainties, requiring rigorous error estimation and potentially limiting the precision with which the strong coupling constant can be determined from this technique. Consequently, while powerful in principle, Finite Energy Sum Rules necessitate a delicate balance between computational feasibility, theoretical control, and the minimization of approximation-induced errors.

Accelerating Convergence: A Mathematical Imperative

The Shanks Transformation is a sequence acceleration technique applied to slowly convergent or divergent series to improve the rate of convergence to a limit. It operates by constructing a new sequence from the original using a specific recursive formula based on finite differences. Given a series $S = \sum_{n=0}^{\in fty} a_n$ , the Shanks Transformation generates a new sequence $T$ where each element $T_n$ is calculated from the original sequence elements. This process effectively resums the series by leveraging relationships between terms, and can significantly reduce the number of terms needed to achieve a desired level of accuracy in approximating the series sum. The method is particularly useful in perturbation theory where series often exhibit slow convergence or asymptotic behavior.

Wynn’s εε-Algorithm is a recursive procedure designed to efficiently compute the Shanks transformed sequence. Unlike direct implementations of the Shanks Transformation which require matrix inversions – computationally expensive operations scaling as $O(n^3)$ – the εε-Algorithm achieves this through a series of simple, iterative updates. Specifically, it maintains a sequence of increasingly accurate approximations to the limit of the original series. Each iteration refines these approximations using only the previous two, resulting in a computational complexity of $O(n)$ per term, and thus a significant performance improvement for large $n$ . This efficiency makes Wynn’s algorithm particularly well-suited for applications involving high-order perturbative calculations where many terms may be required to achieve a desired level of precision.

Direct application of sequence transformations, such as the Shanks Transformation and Wynn’s εε-Algorithm, to perturbative coefficients yields improved estimates of physical quantities by accelerating the convergence of the perturbative series. Standard perturbation theory often suffers from slow convergence, particularly when dealing with strong coupling regimes, necessitating a large number of terms to achieve a desired level of accuracy. These transformations effectively re-sum the perturbative series, creating a new sequence that converges more rapidly to the true physical value. This allows for accurate calculations with a reduced number of terms, minimizing computational cost and improving the reliability of predictions, especially in scenarios where high-order calculations are computationally expensive or analytically intractable. The technique is applicable across various fields employing perturbative expansions, including quantum field theory and statistical mechanics.

Contour-Improved Perturbation Theory (CIPT) addresses the issue of running coupling constants in perturbative calculations by analytically continuing the perturbative series into the complex coupling plane. This continuation, achieved via Padé approximants and optimized contour integration, allows for the summation of a subset of the most important contributions to all orders, effectively mitigating the sensitivity to the arbitrary renormalization scale. By performing the summation along a carefully chosen contour, CIPT provides improved estimates of physical quantities, particularly in regimes where standard perturbative expansions are poorly convergent or divergent, and yields predictions less dependent on the initial perturbative order used in the calculation. The method has been successfully applied to various quantum field theory problems, demonstrating enhanced convergence and accuracy compared to traditional fixed-order perturbation theory.

Stabilizing the Solution: Algorithmic Refinements

The New Wynn’s εε-Algorithm Modification addresses potential instability issues inherent in Wynn’s original algorithm by introducing a regularization parameter. This parameter, typically denoted as ε, effectively dampens the amplification of errors during the iterative process. By controlling the magnitude of corrections applied at each step, the algorithm prevents the algorithm from diverging, particularly when dealing with ill-conditioned systems or noisy data. The inclusion of ε introduces a bias, but allows for a stable and convergent solution, even at the cost of some accuracy which can be minimized through parameter tuning.

Brezinski’s θθ-algorithm represents an extension of Wynn’s algorithm by incorporating second-order finite-difference information into the iterative process. This modification utilizes differences of differences in the sequence of approximants to accelerate convergence toward the limit. Specifically, the algorithm computes a new estimate of $\delta(0)$ by evaluating the difference between consecutive diagonal elements of the continued fraction matrix, effectively incorporating information about the rate of change of the approximants. This approach aims to provide a more accurate and rapidly converging solution compared to standard Wynn algorithms, particularly in scenarios where the original sequence exhibits slow or oscillatory behavior.

The Sedogbo-Sablonnière modification of Wynn’s algorithm addresses potential instability issues inherent in the original method by introducing a user-defined control parameter. This parameter, typically denoted as κ, functions as a regularization term within the algorithm’s iterative process. By adjusting the value of κ, the user can influence the rate of convergence and mitigate the risk of divergence, particularly when dealing with ill-conditioned or noisy input sequences. The inclusion of this control parameter allows for a more robust and reliable estimation of the limit, offering improved performance in scenarios where standard Wynn’s algorithm may fail to converge.

Analysis utilizing modified Wynn algorithms – including εε, θθ, and Sedogbo-Sablonnière variations – has yielded a final estimate for the dominant Quantum Chromodynamics (QCD) correction of $\delta(0) = 0.2107 ± 0.0032 ± 0.0061$ . The stated uncertainty comprises a statistical error of ±0.0032 and a systematic error of ±0.0061. This result represents an improvement in precision and stability compared to calculations performed using the standard Wynn algorithm, which previously exhibited increased susceptibility to divergence and yielded less reliable estimates of $\delta(0)$ .

Impact on Electroweak Precision: A Necessary Advancement

Refinements to existing computational algorithms represent a significant step towards minimizing theoretical uncertainties in the determination of the strong coupling constant, $\alpha_s$ . Traditional methods often rely on perturbative expansions which, while accurate to a degree, introduce ambiguities and require careful estimation of higher-order terms. These newly developed algorithms, leveraging techniques like the Shanks transformation, demonstrate an improved capacity to extrapolate beyond the directly calculated terms, effectively mitigating the impact of truncation errors. This enhanced precision isn’t merely academic; a more accurate $\alpha_s$ value directly translates to more reliable predictions in electroweak physics, influencing calculations related to particle masses, decay rates, and ultimately, the consistency of the Standard Model itself. The demonstrated ability to achieve substantial accuracy with limited input coefficients suggests a promising pathway for further optimization and a more robust understanding of fundamental interactions.

The precision of electroweak predictions is fundamentally linked to an accurate understanding of the strong coupling constant, $\alpha_s$ . This constant governs the strength of the strong force, which dictates interactions between quarks and gluons, and indirectly impacts the properties of particles involved in electroweak processes. Subtle shifts in $\alpha_s$ propagate through calculations of radiative corrections – quantum loop effects that refine theoretical predictions – influencing the predicted values of quantities like the W boson mass and the anomalous magnetic moment of the muon. Consequently, a more precise determination of $\alpha_s$ minimizes theoretical uncertainties, allowing for more stringent tests of the Standard Model and potentially revealing deviations that could signal new physics beyond it. Improving the accuracy of this fundamental constant is therefore not merely a refinement of existing calculations, but a crucial step toward unlocking a deeper understanding of the universe’s fundamental forces.

Hadronic tau decay presents a unique avenue for refining measurements within the Standard Model, particularly regarding the W boson mass and other crucial electroweak parameters. The process, where a tau lepton decays into hadrons, is sensitive to subtle quantum effects influenced by the strong coupling constant $\alpha_s$ . By meticulously analyzing these decay patterns, researchers can indirectly constrain the value of $\alpha_s$ and, consequently, improve the precision of theoretical predictions for electroweak processes. This approach offers a complementary method to direct measurements of the W boson mass, helping to resolve discrepancies and solidify the foundations of particle physics. The refinement of hadronic tau decay analysis therefore directly impacts the accuracy with which fundamental parameters are known, contributing to a more complete and consistent understanding of the universe’s building blocks.

This analysis establishes a remarkably precise determination of the strong coupling constant, $\alpha_s$ , with an estimated uncertainty of 0.0061-a significant advancement in the field. The methodology employed leverages the Shanks transformation, achieving a 13.34% deviation from the exact result despite utilizing input from only three known coefficients. This efficiency highlights the power of the applied mathematical technique in extracting high-precision values from limited data, suggesting a pathway for refining calculations in particle physics where precise knowledge of $\alpha_s$ is paramount for accurate theoretical predictions and interpretations of experimental results.

The pursuit of higher-order corrections in hadronic tau decays, as detailed in the study, mirrors a fundamental mathematical striving for absolute truth. This investigation employs sequence transformations – techniques for refining approximations – to arrive at a more accurate determination of the strong coupling constant. It echoes Nietzsche’s observation: “There are no facts, only interpretations.” The study doesn’t seek a ‘working’ solution, but a provable one, recognizing that each perturbative order is merely an interpretation of the underlying physics. The Shanks transformation, and its variants, represent a systematic attempt to refine this interpretation, edging closer to an objective understanding, where algorithmic beauty, derived from mathematical consistency, reigns supreme.

Beyond the Series

The pursuit of precision in hadronic tau decays, as explored within this work, ultimately reveals a fundamental tension. The reliance on perturbative expansions, while mathematically elegant in principle, necessitates a continuous negotiation with the inherent limitations of asymptotic series. The application of sequence transformations – Shanks and its descendants – represents not a resolution, but a skillful postponement of the inevitable divergence. One is left to ponder if increasingly sophisticated extrapolation techniques merely refine the art of controlled approximation, rather than achieving genuine convergence to a physically meaningful value.

Future investigations would benefit from a more critical examination of the underlying assumptions informing these expansions. The strong coupling constant, α_s, is treated as a parameter to be extracted, yet its own definition within the perturbative framework is subject to the same challenges. Perhaps a deeper understanding of non-perturbative effects, and their interplay with the perturbative series, holds the key to a truly robust determination. To truly advance, the field must address not just how to sum a series, but why it behaves as it does.

The elegance of mathematical formalism should not overshadow the physical realities. Heuristics, while expedient, are compromises, not virtues. The ongoing refinement of these techniques serves as a reminder that the pursuit of knowledge is often a process of navigating limitations, and acknowledging the inherent imperfection of all models.

Original article: https://arxiv.org/pdf/2601.11277.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

The Precise Window into Quantum Chromodynamics

Accelerating Convergence: A Mathematical Imperative

Stabilizing the Solution: Algorithmic Refinements

Impact on Electroweak Precision: A Necessary Advancement

Beyond the Series

See also: