Beyond SCAN: Untangling Self-Interaction Errors in Chemical Reactions

Author: Denis Avetisyan

A new analysis reveals the persistent impact of self-interaction errors on the accuracy of density functional theory calculations for reaction barriers, even with modern functionals like SCAN.

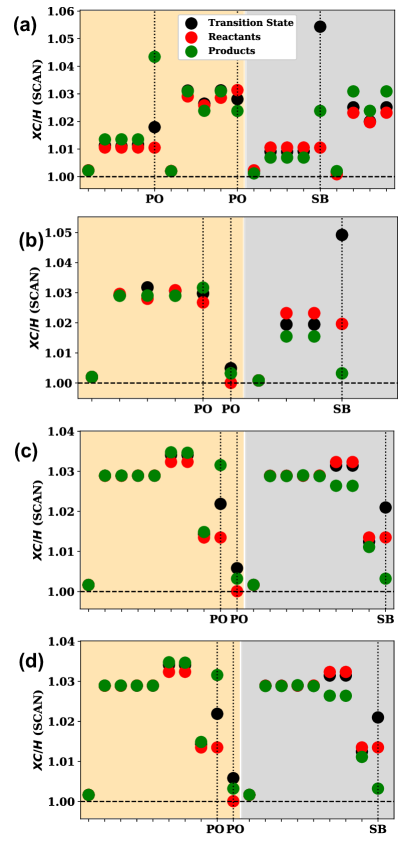
The study reveals how subtle changes in spectator, participant, and stretched bond orbital energies-specifically the <span class="katex-eq" data-katex-display="false">E^{SIC}[n\_{i}]</span>-along reaction pathways connecting reactants, transition states, and products, directly correlate with the magnitude of the SIC correction to forward and reverse reaction barriers. — The study reveals how subtle changes in spectator, participant, and stretched bond orbital energies-specifically the $E^{SIC}[n\_{i}]$ -along reaction pathways connecting reactants, transition states, and products, directly correlate with the magnitude of the SIC correction to forward and reverse reaction barriers.

Researchers explore how Perdew-Zunger self-interaction corrections and the FLOSIC method affect reaction barrier heights within the framework of density functional theory.

Despite advances in density functional theory, accurately predicting chemical reaction barrier heights remains a persistent challenge due to self-interaction errors inherent in commonly used approximations. This work, titled ‘The rise and fall of stretched bond errors: Extending the analysis of Perdew-Zunger self-interaction corrections of reaction barrier heights beyond the LSDA’, presents a detailed orbital analysis of these errors-specifically focusing on the role of ‘stretched bond’ orbitals-when applying Perdew-Zunger self-interaction corrections to three rungs of the Jacob’s Ladder. The analysis reveals that while the SCAN meta-generalized gradient approximation offers improved accuracy, significant self-interaction remains, and its correction is limited by inaccuracies in predicted reaction energies. Can a deeper understanding of stretched bond errors guide the development of density functionals with even greater predictive power for chemical reactions?

Unveiling the Subtle Flaw: The Self-Interaction Error in DFT

Density Functional Theory (DFT) stands as a pivotal technique in materials science, enabling researchers to computationally predict material behaviors and design novel substances. However, a fundamental challenge known as the self-interaction error inherently limits its accuracy. This error stems from the way DFT approximates the complex interactions between electrons; in essence, each electron spuriously interacts with itself. While electrons naturally repel each other, standard DFT approximations fail to fully prevent an electron from incorrectly ‘feeling’ its own electrostatic potential. This unphysical self-interaction leads to an overestimation of electron energies and, consequently, inaccurate predictions of material properties, necessitating the development of correction methods to refine computational results and bolster the reliability of materials modeling.

The inaccuracies inherent in standard Density Functional Theory (DFT) stem from approximations made in describing electron exchange and correlation – the complex interplay governing how electrons interact. Ideally, DFT should precisely calculate the energy of a material based solely on its electron density. However, common approximations fail to prevent an electron from spuriously interacting with itself – the self-interaction error – and inadequately model the intricate many-body effects arising from electron-electron repulsion. This deficiency manifests as incorrect predictions of material properties, including flawed estimations of reaction energies, band gaps, and magnetic moments. Consequently, computational materials design relying on these approximations can produce unreliable results, hindering advancements in fields like catalysis, energy storage, and semiconductor development. Addressing this fundamental limitation remains a central challenge in computational materials science.

The self-interaction error within Density Functional Theory doesn’t simply introduce minor inaccuracies; it fundamentally compromises the predictive power of computational materials design. Specifically, the flawed treatment of electron interactions leads to systematically poor predictions of reaction barriers, hindering the accurate modeling of chemical reactions and catalytic processes. Equally problematic is the incorrect description of charge transfer phenomena, crucial for understanding semiconductors, solar cells, and other electronic materials. These errors manifest as inaccurate estimations of energy levels and charge distributions, ultimately limiting the reliability of simulations used to discover and optimize new materials with desired properties. Consequently, researchers are compelled to either employ computationally expensive methods to mitigate the error or carefully validate DFT results against experimental data, adding significant overhead to materials discovery efforts.

Mitigating the Imperfection: Corrective Strategies for DFT

Several methodologies exist to mitigate the self-interaction error inherent in Density Functional Theory (DFT). The Perdew-Zunger correction is an early approach that subtracts the self-interaction energy calculated from the Kohn-Sham orbitals. Fermi-Löwdin orbital (FLO) methods address the issue by utilizing a localized orbital basis and enforcing orthogonality, reducing spurious interactions. Locally scaled corrections, such as the Localized Hartree-Fock (LHF) approach, modify the exchange-correlation potential to minimize self-interaction on a per-orbital basis. These techniques differ in their computational demands and the extent to which they eliminate the error, with FLO methods generally being more computationally expensive than the Perdew-Zunger correction, but potentially more accurate for certain systems.

Self-interaction error in Density Functional Theory (DFT) arises from the inaccurate description of electron-electron interactions, where an electron spuriously interacts with itself. Mitigation strategies address this by subtracting a correction term, $\Delta E_{SI}$ , from the total energy, $E_{total}$ , effectively reducing this spurious interaction. The corrected energy is then calculated as $E_{corrected} = E_{total} - \Delta E_{SI}$ . This subtraction aims to improve the accuracy of calculations, particularly for systems where self-interaction is pronounced, such as those with localized electrons or open-shell configurations. The specific form of the correction term varies between methods, but all share the goal of more accurately representing the many-body interactions within the system.

Implementing self-interaction correction (SIC) methods introduces increased computational demands due to the additional calculations required to determine and apply the correction terms. The complexity arises from the need to evaluate integrals involving occupied and virtual orbitals, scaling with the system size and basis set. Furthermore, the effectiveness of SIC methods is not universal; performance is demonstrably dependent on both the specific density functional employed and the characteristics of the system under investigation. Certain functionals benefit more significantly from correction than others, and systems exhibiting strong static correlation or significant charge transfer may require specialized SIC implementations or alternative approaches to achieve accurate results.

FLO-SCAN calculations reveal that the ratio of self-exchange-correlation to Hartree energy (<span class="katex-eq" data-katex-display="false">XC/H</span>) varies across reactants, transition states, and products for four representative reactions-CH₄ + OH, H + OH, H + H₄S, and F + H₂-reflecting changes in frontier molecular orbital (FMO) shapes and indicated by vertical lines denoting participant and stretched bond orbitals, with spin-up data on beige and spin-down on gray backgrounds. — FLO-SCAN calculations reveal that the ratio of self-exchange-correlation to Hartree energy ( $XC/H$ ) varies across reactants, transition states, and products for four representative reactions-CH₄ + OH, H + OH, H + H₄S, and F + H₂-reflecting changes in frontier molecular orbital (FMO) shapes and indicated by vertical lines denoting participant and stretched bond orbitals, with spin-up data on beige and spin-down on gray backgrounds.

Toward a More Principled Approach: The SCAN and r2SCAN Functionals

The SCAN (Strongly Constrained and Appropriately Normed) meta-GGA density functional represents a substantial improvement in density functional theory due to its rigorous adherence to 17 known exact constraints on the exchange-correlation functional. These constraints, derived from fundamental physical principles and exact conditions, govern the behavior of the functional in various scenarios, including uniform electron gas, one-electron systems, and asymptotic behavior. Satisfaction of these constraints minimizes self-interaction error and improves the description of static correlation effects, resulting in enhanced accuracy for predicting the properties of a diverse range of materials and systems, including solids, surfaces, and molecules. This level of constraint satisfaction differentiates SCAN from prior functionals and contributes to its improved performance across various chemical and physical applications.

r2SCAN is an evolution of the SCAN meta-GGA density functional, designed to improve performance in systems where SCAN exhibits limitations. This refinement is achieved through a modified exchange-correlation potential construction, specifically altering the treatment of the kinetic energy density. Benchmarking demonstrates that r2SCAN consistently outperforms SCAN in predicting properties of diverse materials, including transition metal oxides, molecular crystals, and strongly correlated systems. Furthermore, r2SCAN demonstrates improved performance in describing systems with significant static correlation, expanding the range of materials accurately addressed by density functional theory beyond the capabilities of the original SCAN functional.

Both SCAN and r2SCAN are classified as semi-local density functionals, indicating their exchange-correlation energy calculation depends solely on the electron density $\rho(\mathbf{r})$ and its gradient at each point in space. While local functionals only utilize the density itself, the inclusion of the gradient allows semi-local functionals to account for inhomogeneities in the electron distribution. Crucially, these functionals are designed to satisfy a comprehensive set of 17 known exact constraints on the exchange-correlation functional. This satisfaction effectively minimizes the spurious self-interaction error-where an electron incorrectly interacts with itself-leading to improved accuracy in predicting material properties and reaction energies compared to more traditional approximations.

Validating Predictive Power: Reaction Barriers and Benchmark Sets

The accurate determination of reaction barrier heights is fundamentally important to the field of chemical kinetics, as these barriers directly govern reaction rates. This predictive capability extends to catalyst design; understanding how reactants transition to products allows for the rational modification of catalytic surfaces to lower activation energies and enhance reaction efficiency. Precisely modeled barrier heights enable the computation of rate constants using transition state theory, facilitating the prediction of reaction performance under various conditions. Consequently, reliable barrier height calculations are critical for both theoretical investigations into reaction mechanisms and the practical development of improved catalytic materials.

Evaluations using the BH76 benchmark set demonstrate that SCAN and r2SCAN meta-GGA functionals provide significantly improved prediction of reaction barrier heights compared to traditional GGA functionals. These functionals consistently exhibit lower mean absolute deviations (MAD) when calculating activation energies for the reactions included in the BH76 set. This outperformance is attributed to their ability to more accurately describe electronic delocalization and non-local interactions, crucial for properly characterizing transition states and, consequently, barrier heights. The BH76 set, comprising 76 diverse chemical reactions, serves as a stringent test of functional performance in predicting kinetic properties.

The FLO-SCAN functional demonstrates enhanced accuracy in predicting reaction barrier heights, achieving a mean absolute deviation (MAD) of 3.09 kcal/mol when assessed against the BH76 benchmark set. This represents a substantial improvement over other density functionals; FLO-LDA and FLO-PBE yield MAD values of 5.10 kcal/mol and 4.14 kcal/mol, respectively, indicating a notably reduced error rate in barrier height predictions when utilizing the FLO-SCAN functional.

The accuracy of density functional theory (DFT) calculations for reaction barriers is dependent on the proper description of molecular orbitals. These orbitals are categorized based on their behavior during a reaction: participant orbitals, which directly contribute to bond breaking and formation and thus significantly influence barrier heights; spectator orbitals, which remain largely unchanged throughout the reaction and have a minimal effect on barrier prediction; and stretched bond orbitals, which are particularly important for describing the transition state geometry and associated energy changes as bonds lengthen or weaken. Accurate representation of these orbital types, especially the participant and stretched bond orbitals, is crucial for obtaining reliable barrier height predictions and, consequently, for modeling reaction kinetics.

Ascending the Ladder: The Future Trajectory of DFT and Materials Discovery

Density Functional Theory (DFT) relies on approximations known as functionals to calculate the electronic structure of materials, and these functionals vary significantly in their complexity and accuracy. The conceptual framework known as Jacob’s Ladder organizes these functionals into a hierarchy, with each rung representing increased sophistication and, generally, improved predictive power. Recent developments, such as the SCAN and r2SCAN functionals, exemplify this progression; they move beyond traditional generalized gradient approximations by explicitly satisfying all known exact constraints that a density functional should obey. This careful construction-incorporating conditions related to uniform electron density, strong-interaction limits, and more-results in a functional that captures electron correlation effects more accurately than its predecessors, offering a more reliable pathway to understanding and predicting material behavior. The continued ascent up Jacob’s Ladder, therefore, represents a systematic strategy for refining DFT and unlocking its full potential.

Density Functional Theory (DFT) continually advances through the development of increasingly sophisticated functionals, organized conceptually as Jacob’s Ladder. Each ascent on this ladder represents the satisfaction of more rigorous physical constraints, leading to markedly improved predictions of material properties. Lower rungs, like the Local Density Approximation, offer computational efficiency but often sacrifice accuracy. As functionals climb – incorporating gradient corrections, meta-GGAs, hybrids, and ultimately range-separated hybrids – they address deficiencies in their predecessors. This progression isn’t merely academic; by adhering to fundamental physical principles, such as satisfying exact constraints on the exchange-correlation energy, these higher-rung functionals minimize self-interaction error and capture subtle many-body effects. Consequently, materials scientists and chemists can rely on these advanced methods to model complex systems with greater confidence, fostering innovation in diverse fields from superconductivity to drug design.

Computational studies reveal a substantial contribution from self-interaction error to inaccuracies in predicting energy barrier heights – a critical factor in understanding reaction rates and chemical processes. Analysis of functionals like FLO-LDA and FLO-PBE demonstrates that approximately 79% of the error in calculated barrier heights stems directly from this self-interaction, where an electron spuriously interacts with itself. This finding underscores the vital need to develop density functionals that effectively minimize self-interaction error, as correcting this flaw dramatically improves the reliability of computational predictions and enables more accurate modeling of chemical kinetics and material stability. Addressing this issue isn’t merely a refinement of existing methods; it represents a crucial step toward achieving truly predictive capability in computational chemistry and materials science.

The continued refinement of density functional theory (DFT), moving up Jacob’s Ladder towards greater accuracy, holds substantial promise for revolutionizing materials science. Improved functionals are not merely incremental improvements; they represent a pathway to in silico materials design with unprecedented predictive power. This enhanced capability is poised to dramatically accelerate discovery in critical fields like energy storage, where optimized battery materials with higher energy density and longer lifespans can be virtually screened and designed. Similarly, in catalysis, precise modeling of reaction pathways and surface interactions-previously hampered by functional limitations-becomes attainable, enabling the rational design of more efficient and selective catalysts. Ultimately, this progression towards higher rungs on the ladder facilitates a materials innovation cycle-from initial conception to optimized performance-that is faster, more cost-effective, and less reliant on trial-and-error experimentation.

The pursuit of accuracy in computational chemistry, as demonstrated by this research into density functional theory, echoes a fundamental principle: elegance in method reveals a deeper understanding of the underlying phenomena. The study’s exploration of self-interaction corrections and the nuanced behavior of functionals like SCAN highlights the necessity of refining approximations to achieve truly predictive power. As Pyotr Kapitsa observed, “It is in the interests of science that one should not be too confident.” This caution is acutely relevant here; even sophisticated methods like FLOSIC offer only partial correction, underscoring the persistent challenges in accurately modeling complex chemical reactions and the importance of continuous refinement as one ascends Jacob’s Ladder.

Where the Path Leads

The persistent, if subtle, failings revealed by this work suggest a discomforting truth: chasing perfection along Jacob’s Ladder may yield diminishing returns. The SCAN functional, while a considerable achievement, isn’t immune to the quiet distortions of self-interaction error. The application of FLOSIC offers some palliative care, a refinement rather than a cure, and highlights a deeper issue – the accuracy of barrier heights remains tethered to the accuracy of the underlying energetic landscape. One anticipates a future where corrections aren’t simply added to existing functionals, but are instead woven into their very fabric, demanding a more holistic, architectural approach to functional design.

A truly elegant solution, one suspects, will not focus solely on minimizing error in specific cases, but on creating a framework that inherently resists it. The current emphasis on benchmarking against ever-larger datasets, while valuable, risks mistaking statistical robustness for genuine understanding. A consistent theory, one that whispers its truths even when challenged, is preferable to a shouting match of numerical precision.

The field now faces a choice: continue refining existing approximations, or dare to reimagine the foundations. Perhaps the most fruitful path lies not in seeking the most accurate functional, but in constructing one that is, simply, sufficient – a design that prioritizes clarity and consistency, recognizing that good architecture is invisible until it fails.

Original article: https://arxiv.org/pdf/2601.11454.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/