Quantum Chains: Untangling Interactions in Rydberg Atom Systems

Author: Denis Avetisyan

New research reveals how strongly interacting chains of Rydberg atoms can exhibit surprisingly predictable dynamics under certain conditions.

The study reveals that subtle deviations from a simplified <span class="katex-eq" data-katex-display="false">\hat{H}_{PXQ}</span> Hamiltonian-attributable to longer-range interactions-manifest as measurable changes in the average classical number of excitations, leakage from the single dimer subspace, and the averaged Rydberg population difference, despite nearly identical dynamics predicted by both the simplified and full <span class="katex-eq" data-katex-display="false">\hat{H}_{0}</span> Hamiltonians across a system of length ten. — The study reveals that subtle deviations from a simplified $\hat{H}_{PXQ}$ Hamiltonian-attributable to longer-range interactions-manifest as measurable changes in the average classical number of excitations, leakage from the single dimer subspace, and the averaged Rydberg population difference, despite nearly identical dynamics predicted by both the simplified and full $\hat{H}_{0}$ Hamiltonians across a system of length ten.

This study demonstrates that antiferromagnetic dimers in Rydberg atom chains can be effectively described by the integrable PXQ Hamiltonian, with analysis of deviations caused by long-range interactions.

Understanding the dynamics of strongly correlated quantum systems remains a central challenge in many-body physics. In ‘Dynamics of antiferromagnetic Dimers in Rydberg Atom Chains’, we investigate the emergent behavior of antiferromagnetic dimers within a highly controllable Rydberg atom chain, demonstrating that under specific conditions, the system’s dynamics are well-described by an integrable PXQ Hamiltonian. We find deviations from this simplified model arise from both leakage from the constrained dimer-conserving Hilbert space and the influence of long-range interactions, yet the dimer number remains conserved. This work opens pathways for exploring quantum many-body scars and integrability in Rydberg atom quantum simulators-but how can these systems be further tailored to isolate and characterize more complex, non-integrable dynamics?

The Architecture of Constraint: Introducing Rydberg Atom Chains

The Rydberg atom chain represents a novel experimental system for investigating the complex behavior of strongly correlated quantum systems. By arranging individual atoms in a chain and exciting them to highly energetic Rydberg states, researchers can leverage the unique interactions arising from their large size and strong dipole moments. This configuration gives rise to the Rydberg blockade, a phenomenon where the excitation of one atom inhibits the excitation of its neighbors due to electrostatic repulsion. The blockade effectively introduces strong correlations between the atoms, meaning their behavior is intrinsically linked and cannot be described by considering each atom in isolation. Consequently, the Rydberg atom chain offers a controllable platform to explore emergent quantum phenomena, providing insights into many-body physics and potentially paving the way for advanced quantum technologies.

The Rydberg blockade, arising from the strong interactions between highly excited, or Rydberg, atoms, fundamentally alters the collective behavior of an atomic chain. When one atom in the chain is excited to a Rydberg state, it effectively prevents its neighbors from undergoing the same transition due to the long-range Coulomb interaction – this is the blockade. This constraint isn’t simply a suppression of excitation; it gives rise to emergent phenomena not predictable from considering individual atoms in isolation. Instead of independent excitations, the system exhibits collective modes and correlations, potentially leading to complex quantum phases and novel computational strategies. The blockade transforms the chain from a collection of individual quantum systems into a strongly correlated many-body system, where the interactions dictate the overall dynamics and create behaviors exceeding the sum of their parts – a cornerstone of quantum complexity.

The ability to manipulate quantum systems hinges on a thorough comprehension of the inherent constraints governing their collective behavior. In many-body systems, interactions between constituents-like the Rydberg blockade exhibited in atom chains-don’t simply add up; they create emergent phenomena that demand a shift in perspective. Precisely characterizing these constraints allows researchers to move beyond predicting individual particle behavior and towards designing collective quantum states with specific functionalities. This control isn’t merely academic; it’s the foundation for advancements in quantum simulation, computation, and sensing, where harnessing correlated quantum dynamics promises capabilities far exceeding those of classical systems. Ultimately, understanding how constraints shape quantum behavior unlocks the potential to engineer entirely new forms of quantum technology.

A one-dimensional chain of Rydberg atoms, separated by a distance <span class="katex-eq" data-katex-display="false">r_0</span>, exhibits interactions <span class="katex-eq" data-katex-display="false">V_0</span> arising from van der Waals forces when excited from the ground state <span class="katex-eq" data-katex-display="false">\ket{\downarrow}</span> to the Rydberg state <span class="katex-eq" data-katex-display="false">\ket{\uparrow}</span> with Rabi frequency Ω and detuning Δ. — A one-dimensional chain of Rydberg atoms, separated by a distance $r_0$ , exhibits interactions $V_0$ arising from van der Waals forces when excited from the ground state $\ket{\downarrow}$ to the Rydberg state $\ket{\uparrow}$ with Rabi frequency Ω and detuning Δ.

Simplifying the Complex: The PXP Hamiltonian as a Guiding Model

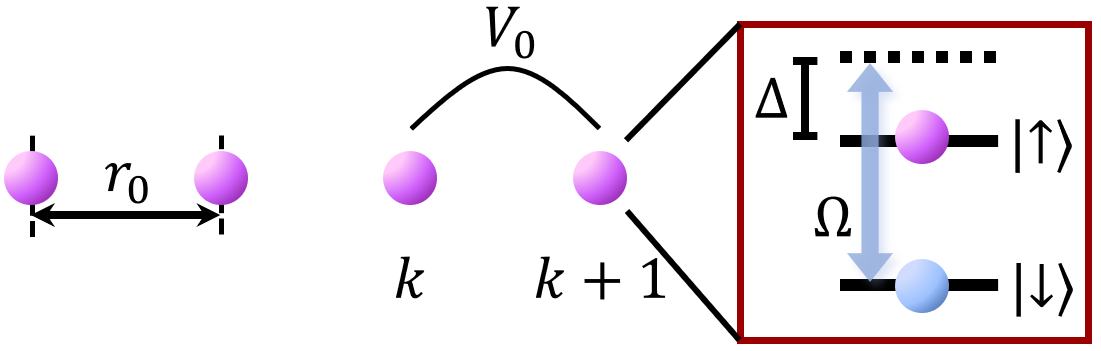
The PXP Hamiltonian serves as an effective model for describing the behavior of Rydberg chains, systems where atoms are excited to high-energy Rydberg states. This model simplifies the complex many-body interactions within the chain by focusing on nearest-neighbor interactions: a pairwise excitation (P), a pairwise de-excitation (X), and a constraint preventing multiple excitations on the same site (Q). This reduction to a limited set of interactions accurately captures the essential physics of constrained interactions in Rydberg chains, specifically the blockade effect that limits excitation to a single atom within a given range, while substantially reducing computational complexity compared to modeling the full, unconstrained system. The resulting Hamiltonian, $H = \sum_i h_i + \sum_{i,j} V_{i,j}$ , incorporates on-site energy $h_i$ and pairwise interaction terms $V_{i,j}$ that govern the collective behavior of the atoms.

The non-integrable nature of the PXP Hamiltonian implies the absence of conserved quantities that would allow for exact analytical solutions to the many-body problem. Consequently, its dynamics are characterized by sensitivity to initial conditions and the emergence of chaotic behavior. This necessitates the use of numerical methods, such as time-dependent density functional theory or exact diagonalization, to investigate the system’s evolution and predict its properties. The lack of analytical tractability complicates the identification of long-time behaviors and necessitates careful analysis of numerical simulations to discern meaningful physical insights.

The PXQ Hamiltonian builds upon the PXP model by incorporating interactions that are dependent on both the detuning (Δ) and Rabi frequency (Ω) of the Rydberg excitation. This refinement allows for a more accurate approximation of the Rydberg chain’s behavior, particularly when the interaction strength ( $V_0$ ) significantly exceeds the Rabi frequency ( $V_0 >> \Omega$ ). This study demonstrates that under these conditions, the PXQ Hamiltonian effectively captures the essential physics, providing a viable pathway for analyzing the dynamics of strongly interacting Rydberg atoms without requiring full simulations of the original, more complex system.

Simulations reveal that deviations from the <span class="katex-eq" data-katex-display="false">\hat{H}_{PXQ}</span> Hamiltonian, observed in the maximal dimer subspace through metrics like classical number of dimers, leakage from the dimer subspace, and Rydberg population difference, are attributable to longer-range interactions despite nearly identical dynamics with the <span class="katex-eq" data-katex-display="false">\hat{H}_{0}</span> Hamiltonian. — Simulations reveal that deviations from the $\hat{H}_{PXQ}$ Hamiltonian, observed in the maximal dimer subspace through metrics like classical number of dimers, leakage from the dimer subspace, and Rydberg population difference, are attributable to longer-range interactions despite nearly identical dynamics with the $\hat{H}_{0}$ Hamiltonian.

Beyond Thermalization: Scars in the Quantum Landscape

The PXQ Hamiltonian demonstrates a weak violation of the Eigenstate Thermalization Hypothesis (ETH). The ETH predicts that the statistical properties of energy eigenstates in a quantum chaotic system should conform to a thermal distribution, meaning that expectation values of observables are smooth functions of the eigenstate and are well-represented by the microcanonical ensemble. However, analysis of the PXQ model reveals deviations from this expected behavior. Specifically, certain eigenstates exhibit atypical properties, resulting in non-thermal features in the system’s energy spectrum and observable statistics. This weak ETH violation suggests the presence of underlying quantum many-body effects that impede the complete thermalization of the system, even in the presence of strong disorder and interactions.

Quantum Many-Body Scars represent a breakdown of the Eigenstate Thermalization Hypothesis (ETH) in otherwise chaotic quantum systems. ETH predicts that eigenstates of a chaotic Hamiltonian should statistically resemble microcanonical ensembles, implying thermalization; however, scarred eigenstates exhibit atypical properties, such as increased overlap with specific initial states and a localization in Hilbert space that prevents them from participating in thermalization. These non-thermal eigenstates are characterized by their persistence despite the chaotic nature of the system and are often associated with specific symmetries or conserved quantities within the Hamiltonian, leading to a non-ergodic behavior where the system fails to explore all accessible states.

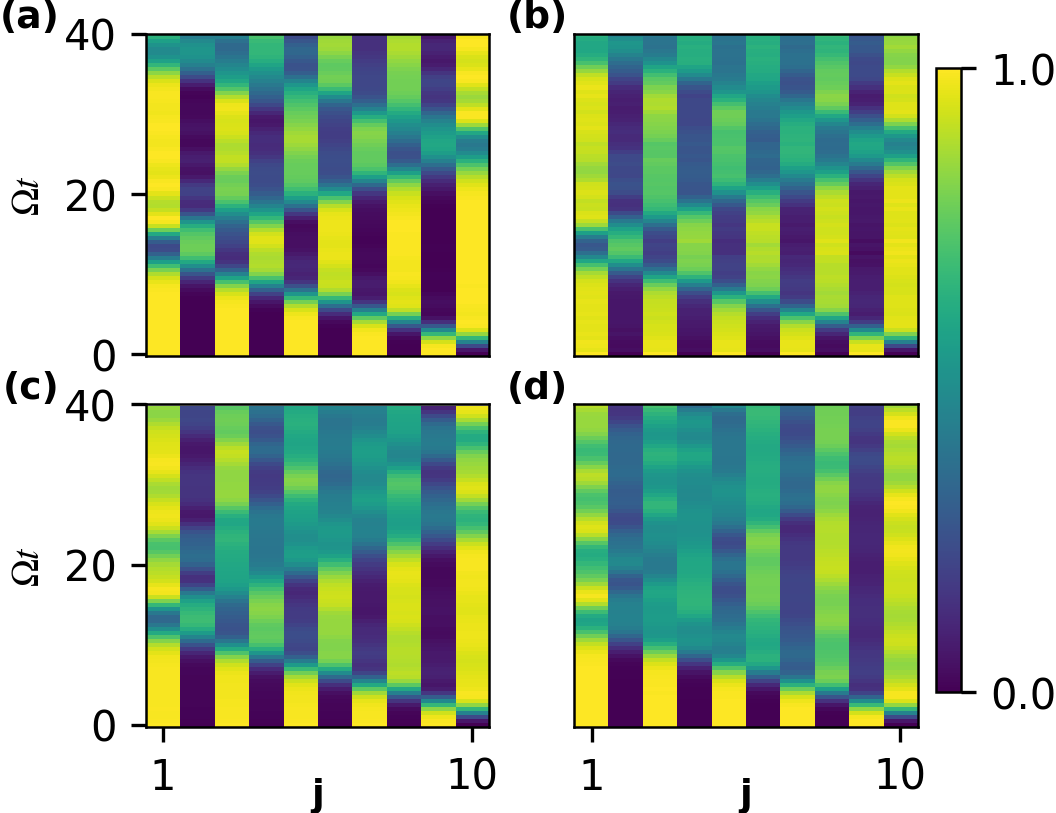
The PXP chain, when subject to a transverse field to create the PXQ model, conserves the number of antiferromagnetic dimers-pairs of adjacent spins with opposing orientations. This conservation arises from the specific interactions within the Hamiltonian; the hopping term in the PXP chain and the added transverse field do not change the total number of these dimer structures. Consequently, the Hilbert space of the PXQ model decomposes into sectors, each characterized by a fixed number of antiferromagnetic dimers. This conservation introduces a non-trivial constraint on the system’s dynamics and eigenstates, leading to deviations from typical thermal behavior expected in chaotic many-body systems, as the conserved quantity restricts the accessible state space.

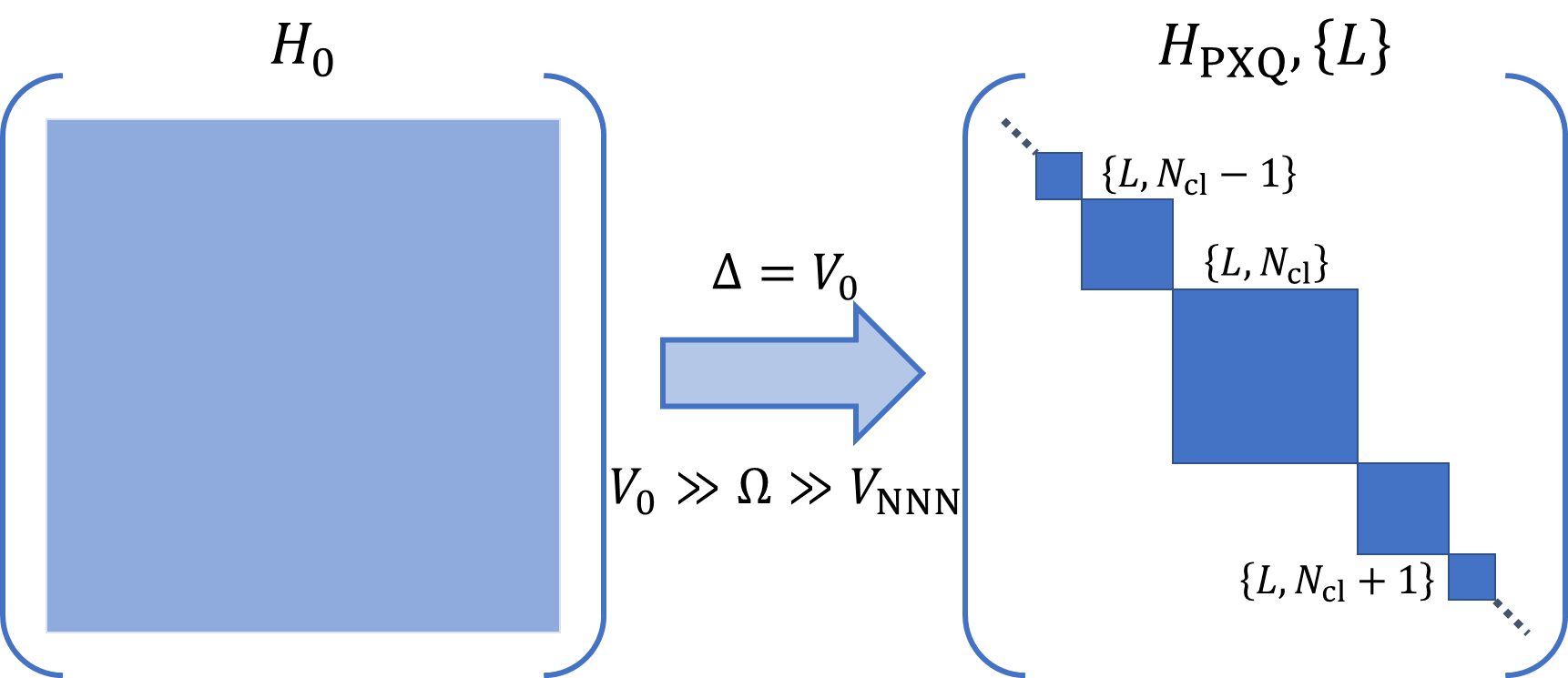
Under conditions where <span class="katex-eq" data-katex-display="false">\Delta = V_0</span> and <span class="katex-eq" data-katex-display="false">V_0 \\gg \\Omega \\gg V_{NNN}</span>, the Hamiltonian <span class="katex-eq" data-katex-display="false">\hat{H}_0</span> exhibits a block-diagonal structure due to the conservation of antiferromagnetic dimers. — Under conditions where $\Delta = V_0$ and $V_0 \\gg \\Omega \\gg V_{NNN}$ , the Hamiltonian $\hat{H}_0$ exhibits a block-diagonal structure due to the conservation of antiferromagnetic dimers.

Deconstructing the Hilbert Space: A New Organizational Principle

The behavior of the PXQ Hamiltonian is fundamentally shaped by a natural decomposition of its Hilbert space, organized by the number of antiferromagnetic dimers present in a given quantum state. This decomposition isn’t merely a mathematical convenience; it reveals a crucial organizational principle governing the system’s dynamics. Each subspace, defined by a specific dimer count, exhibits distinct energetic characteristics and participates uniquely in the overall quantum evolution. Consequently, understanding how quantum states distribute across these subspaces is key to unraveling the system’s complex behavior, particularly concerning the emergence of Quantum Many-Body Scars-unusual, non-thermalizing eigenstates-and the broader breakdown of expected thermalization processes. The dimer-based decomposition provides a powerful lens through which to analyze the effective interactions and correlations that drive the PXQ Hamiltonian’s peculiar properties.

The natural decomposition of the Hilbert space, based on the number of antiferromagnetic dimers, offers a novel lens through which to examine the perplexing phenomenon of Quantum Many-Body Scars. These scars-unusual eigenstates that resist thermalization-arise when a system avoids the expected chaotic behavior and retains memory of its initial state. This decomposition reveals that the presence of these stable states is directly linked to specific configurations of dimers, creating pathways for information preservation. Consequently, the breakdown of thermalization-the loss of initial state information-can be understood as a consequence of transitioning between these dimer-defined Hilbert space sectors. The framework allows researchers to predict and potentially control the emergence of scars by manipulating the dimer structure, opening avenues for exploring non-equilibrium dynamics and harnessing quantum coherence in many-body systems.

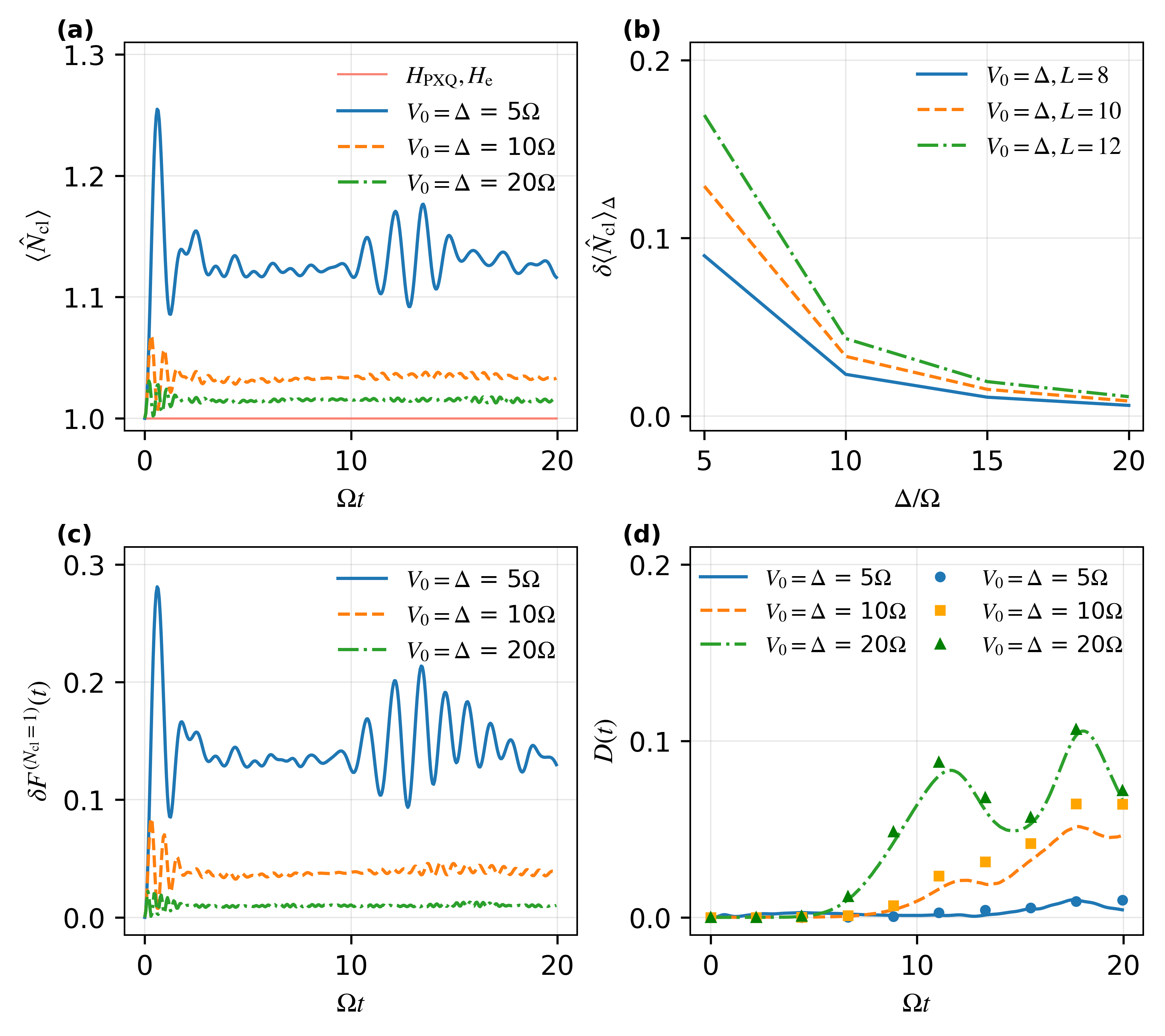
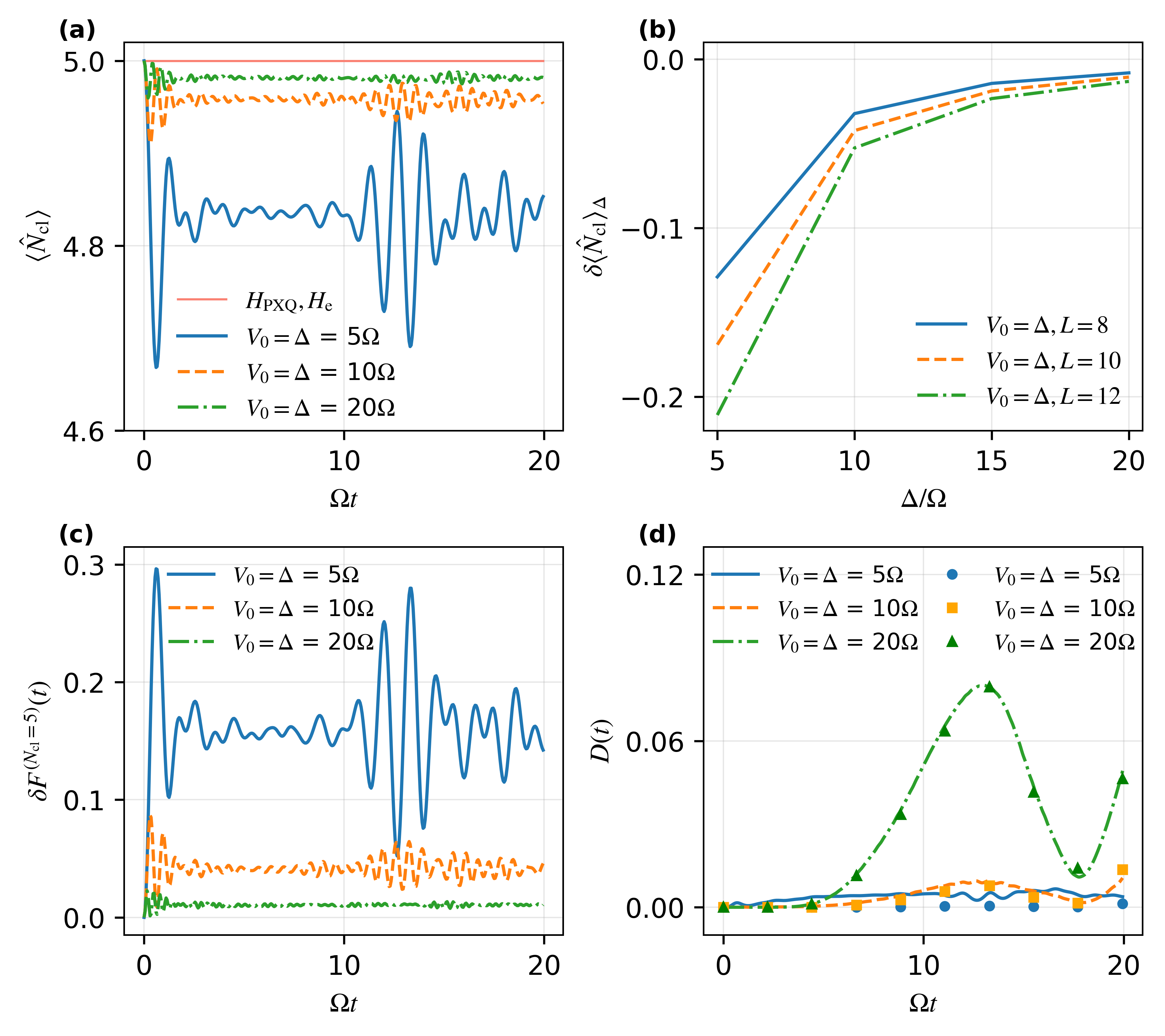
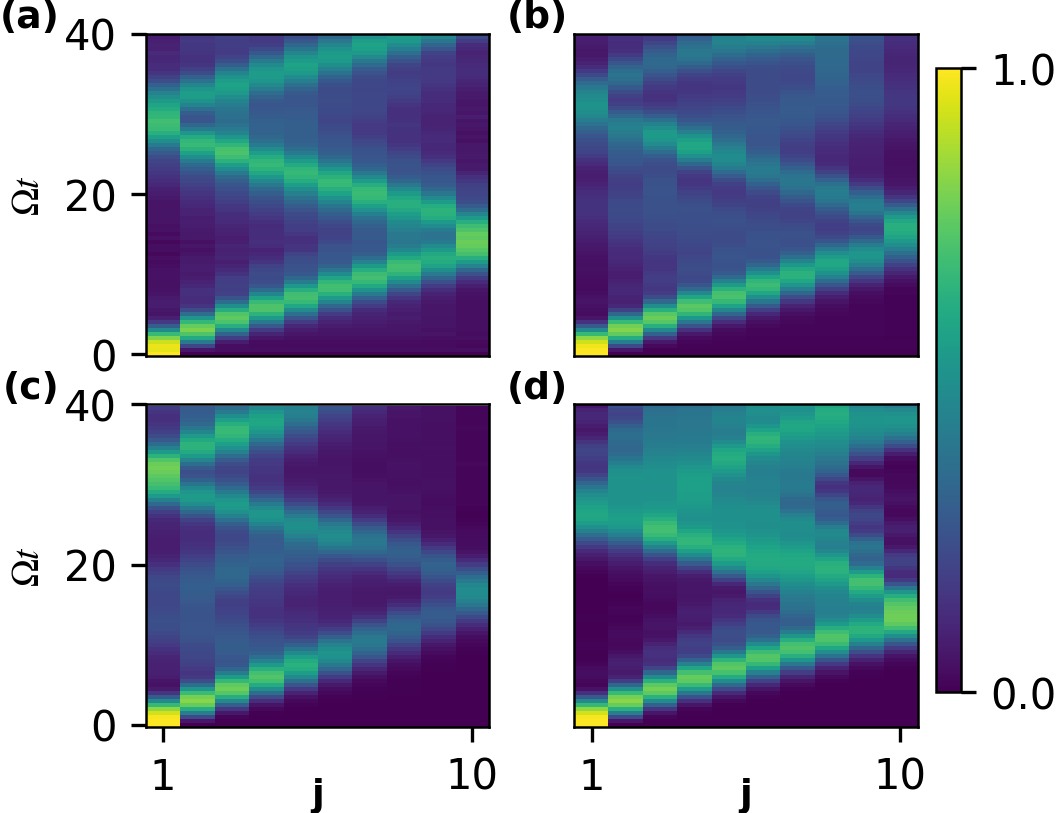
Investigations into the PXQ Hamiltonian reveal a departure from expected behaviors dictated by long-range interaction models, underscoring the critical role of employing an effective Hamiltonian to accurately capture the system’s dynamics. Analysis demonstrates that the time-averaged deviation, denoted as $δ⟨N_{cl}⟩_0$ , exhibits a decreasing trend as the parameter V0 increases; this finding provides strong evidence supporting the enhanced precision of the PXQ approximation in describing the many-body quantum system. This reduction in deviation signifies that the effective Hamiltonian successfully minimizes inaccuracies arising from simplified interactions, allowing for a more reliable prediction of the system’s evolution and properties compared to traditional approaches that solely focus on long-range forces.

Simulations of population dynamics <span class="katex-eq" data-katex-display="false">\langle Q^j \rangle</span> reveal that varying the strength <span class="katex-eq" data-katex-display="false">V_0</span> of the Hamiltonian <span class="katex-eq" data-katex-display="false">\hat{H}_0</span> modulates the observed population behavior, with distinct results compared to using the <span class="katex-eq" data-katex-display="false">\hat{H}_{PXQ}</span> Hamiltonian, as shown for a system size of <span class="katex-eq" data-katex-display="false">L=10</span>. — Simulations of population dynamics $\langle Q^j \rangle$ reveal that varying the strength $V_0$ of the Hamiltonian $\hat{H}_0$ modulates the observed population behavior, with distinct results compared to using the $\hat{H}_{PXQ}$ Hamiltonian, as shown for a system size of $L=10$ .

Towards Analytical Mastery: The Promise of Transformations

The Kramers-Wannier transformation offers a powerful analytical tool for simplifying complex quantum mechanical systems. Specifically, this technique facilitates the mapping of the $PXQ$ Hamiltonian – a common descriptor of systems exhibiting constrained motion – to a more manageable form. By strategically altering the coordinate representation, the transformation effectively reduces the complexity of the original Hamiltonian, allowing researchers to bypass computationally intensive numerical methods and instead derive analytical solutions for key system properties. This simplification is crucial for gaining insights into the dynamics of constrained quantum systems and for developing predictive models without relying on extensive simulations, ultimately advancing the understanding of phenomena across diverse fields like molecular physics and condensed matter science.

The Kramers-Wannier transformation isn’t merely a mathematical trick; it fundamentally reshapes the problem, revealing underlying symmetries and simplifying the complex interactions within the quantum system. By mapping the original Hamiltonian to a more tractable form, researchers gain access to analytical solutions that would otherwise remain elusive. This newfound clarity extends beyond simple calculation, offering crucial insights into the system’s inherent properties and, importantly, potential avenues for external control. Understanding how the transformed Hamiltonian responds to specific parameters allows for the design of targeted interventions, enabling manipulation of the quantum dynamics and potentially unlocking functionalities in diverse physical contexts – from molecular dynamics to condensed matter physics. The ability to predict and influence the system’s behavior, facilitated by this transformation, represents a significant step towards harnessing constrained quantum dynamics for practical applications.

Advancements in leveraging transformations like the Kramers-Wannier method promise novel approaches to controlling quantum dynamics across a range of physical systems. Investigations reveal that as the potential barrier, $V_0$ , increases, the system’s confinement within the modeled subspace-specifically, a single dimer-is strengthened, evidenced by a diminishing leakage quantified by the parameter $\delta F$ . This reduction in leakage not only validates the simplifying approximations inherent in the transformation but also suggests a pathway towards designing systems where quantum behavior is predictably constrained. Consequently, researchers anticipate that continued refinement of these techniques will yield innovative strategies for manipulating and harnessing quantum phenomena in areas such as molecular control, materials science, and quantum information processing.

Simulations of population dynamics <span class="katex-eq" data-katex-display="false">\langle Q^j \rangle \langle \hat{Q}_{j} \rangle</span> with initial state <span class="katex-eq" data-katex-display="false">\ket{\psi_{0}}=\ket{\uparrow\downarrow\downarrow\cdot s}</span> reveal that increasing the voltage <span class="katex-eq" data-katex-display="false">V_0</span> from 5 to 20 Ω modulates the system's behavior, as evidenced by comparing results obtained with Hamiltonian <span class="katex-eq" data-katex-display="false">\hat{H}_{0}</span> to those from <span class="katex-eq" data-katex-display="false">\hat{H}_{\text{PXQ}}</span> at a fixed length of L=10. — Simulations of population dynamics $\langle Q^j \rangle \langle \hat{Q}_{j} \rangle$ with initial state $\ket{\psi_{0}}=\ket{\uparrow\downarrow\downarrow\cdot s}$ reveal that increasing the voltage $V_0$ from 5 to 20 Ω modulates the system’s behavior, as evidenced by comparing results obtained with Hamiltonian $\hat{H}_{0}$ to those from $\hat{H}_{\text{PXQ}}$ at a fixed length of L=10.

The study of Rydberg atom chains, and specifically the emergence of integrability via the PXQ Hamiltonian, echoes a fundamental truth about complex systems. One anticipates a neat, predictable order, a liberation from the usual entropy. Yet, even within this seemingly integrable framework, long-range interactions introduce deviations – cracks in the facade of perfect control. As Wilhelm Röntgen observed, “I have made a discovery which will revolutionize medical science.” This resonates with the current work; the promise of a simplified, integrable model is alluring, but reality, as always, demands acknowledging the inevitable complexities that creep in, the ‘failures’ inherent in any attempt to impose perfect order upon a chaotic universe. The pursuit isn’t about building a stable system, but understanding its delicate, transient equilibrium.

What’s Next?

The identification of an effective PXQ Hamiltonian, even under constrained conditions, offers a momentary respite from the usual disarray. It is not a destination, however, but a carefully charted point within a far larger, less predictable phase space. The system, after all, remains stubbornly finite. The long-range interactions, those inevitable fissures in the idealized model, are not merely perturbations to be minimized, but the very seeds of future, complex behaviors. Attempts to ‘correct’ for them will likely yield only increasingly intricate parameterizations, obscuring the underlying, emergent dynamics.

The focus will inevitably shift toward probing the boundaries of integrability. Where does the neatness of the PXQ model truly break down? What novel forms of many-body scars – those fragile islands of coherence in a sea of entropy – might arise from these deviations? The real challenge isn’t finding systems that fit a Hamiltonian, but understanding how systems become non-integrable, how chaos isn’t failure-it’s nature’s syntax.

A guarantee of complete control, of a perfectly predictable quantum state, remains elusive-a guarantee is simply a contract with probability. Stability, as observed in these Rydberg atom chains, is merely an illusion that caches well. The future lies not in seeking to build stable systems, but in learning to grow resilient ones, accepting that their ultimate fate is, like all things, a graceful disintegration.

Original article: https://arxiv.org/pdf/2601.15866.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/