Author: Denis Avetisyan
New research utilizes a simplified model to chart the complex phase transitions of quark matter under conditions found in neutron stars and heavy ion collisions.
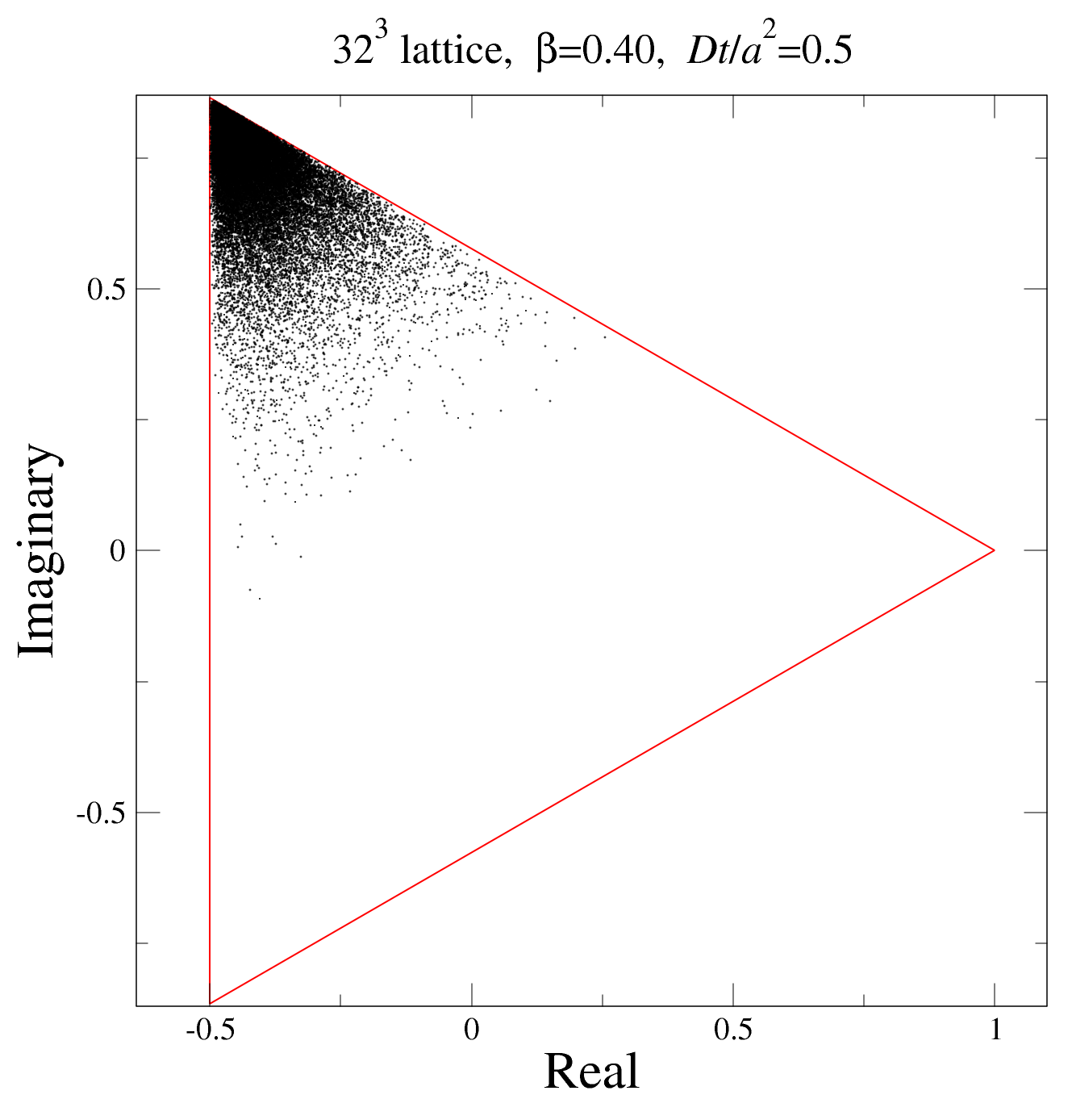
This study investigates the phase structure of heavy quark matter at finite density using a three-state Potts model to understand transitions between different quark matter phases.
Understanding the phase structure of quantum chromodynamics (QCD) at high density remains a central challenge in strong interaction physics. This work, ‘Phase structure of lattice QCD in the heavy quark high-density region and the three-state Potts model’, investigates this problem by mapping QCD onto an effective three-state Potts model, allowing for detailed analysis of the phase transition. The study reveals a complex phase diagram characterized by a transition from first-order to crossover behavior and back to first-order as density increases, suggesting a first-order transition in the high-density, heavy quark region. These findings offer valuable insights into the properties of quark matter under extreme conditions, but what are the implications of this complex phase structure for neutron star mergers and other astrophysical phenomena?
The Sign Problem: A Density-Induced Headache
Simulating Quantum Chromodynamics (QCD) – the theory governing the strong force – becomes extraordinarily difficult when exploring conditions of high density and the presence of heavy quarks, a challenge stemming from what is known as the “sign problem”. This issue arises because the mathematical techniques used to perform these calculations, specifically those employing Monte Carlo methods, involve integrating over complex numbers. As density increases or quark masses grow, the integral oscillates wildly, yielding positive and negative contributions that largely cancel each other out. However, because probabilities must be positive, simply averaging these results produces meaningless outcomes. This necessitates increasingly fine-grained simulations – requiring exponentially more computational power – to overcome the statistical noise and obtain reliable physical predictions. Consequently, understanding the behavior of matter under extreme conditions, such as those found in neutron stars or the early universe, relies on developing innovative techniques to circumvent or mitigate the effects of this persistent and formidable ‘sign problem’.
Investigating the strong nuclear force, as described by Quantum Chromodynamics (QCD), at high densities and with massive quarks presents a formidable challenge for computational physicists. Traditional lattice QCD, a powerful numerical technique, suffers from an exponential increase in computational cost as the complexity of the simulation grows. This arises because accurately representing the quantum state of matter requires an ever-increasing number of lattice points, and the calculations at each point become drastically more demanding with heavier quarks and higher densities. Consequently, exploring the behavior of matter under the extreme conditions found in neutron stars or the early universe – where heavy quark content is significant – becomes prohibitively expensive, severely limiting the scope and precision of current investigations. This computational bottleneck necessitates the development of novel algorithms and innovative approaches to overcome the limitations of standard lattice QCD methods.
The quest to map the phase diagram of heavy dense Quantum Chromodynamics (QCD) extends far beyond theoretical curiosity, proving vital to understanding some of the universe’s most extreme environments. Neutron stars, remnants of supernova explosions, possess densities exceeding those found in atomic nuclei, subjecting their interiors to precisely the conditions described by heavy dense QCD. Determining the state of matter within these stellar objects – whether it consists of quarks and gluons in a deconfined plasma or more exotic forms – necessitates accurate modeling of QCD at extreme densities. Simultaneously, the very early universe, fractions of a second after the Big Bang, also existed in a state of similarly intense density and temperature. Reconstructing the conditions of this primordial epoch, and understanding the transition from the quark-gluon plasma to the hadronic matter that constitutes all ordinary matter today, relies heavily on the same theoretical framework. Consequently, innovative computational and theoretical approaches are crucial to overcome the challenges inherent in studying this regime of QCD and unlock the secrets of both neutron stars and the birth of the cosmos.
![The distribution of the local Polyakov loop differs significantly between the symmetric <span class="katex-eq" data-katex-display="false"> \beta=5.60 </span> phase and the broken <span class="katex-eq" data-katex-display="false"> \beta=6.00 </span> phase of quenched QCD [8].](https://arxiv.org/html/2601.15720v1/figs/plpdissu3b600a.png)
Simplifying the Beast: An Effective Theory Approach
The Effective Theory of Heavy Dense QCD achieves computational simplification by selectively retaining the most relevant degrees of freedom for describing the system at high density and heavy quark mass. This is accomplished through a systematic expansion where contributions arising from spatial link terms – representing fluctuations in the gauge field – are neglected. These terms, while present in the full QCD Lagrangian, become subleading in the limit of heavy quark masses and high densities, allowing for a reduced model that maintains predictive power while significantly decreasing computational complexity. The resulting effective theory focuses on the dynamics of color singlet quark-antiquark pairs and their interactions, offering a tractable framework for investigating the deconfined phase of QCD.
The Heavy Dense QCD effective theory demonstrates a strong correspondence with the three-state Potts model, a well-established system in statistical mechanics. This connection arises because the Potts model, defined on a lattice and characterized by spins taking on three discrete values, possesses computational advantages over directly solving the full QCD equations. Specifically, calculations involving the QCD phase transition – which are notoriously complex – can be mapped onto, and therefore approximated by, simulations of the three-state Potts model. This simplification allows researchers to leverage the established techniques and algorithms developed for the Potts model to gain insights into the behavior of quark-gluon plasma and the nature of confinement, offering a pathway to analyze phenomena otherwise computationally intractable.
The Polyakov Loop, a gauge-invariant operator characterizing long-range order in Quantum Chromodynamics (QCD), is directly analogous to a Z_3 spin variable within the three-state Potts model. This mapping allows the behavior of quarks and gluons during the QCD phase transition to be studied using the well-established techniques of statistical mechanics. Specifically, the expectation value of the Polyakov Loop, which signals the deconfinement of quarks, corresponds to the magnetization of the Z_3 spins. This equivalence simplifies the analysis of the QCD phase transition by leveraging the computational advantages of the Potts model, enabling simulations and theoretical predictions that would be intractable in full QCD.
Modeling the Transition: A Potts Model Playground
The three-state Potts model provides a simplified, yet informative, framework for studying the quantum chromodynamics (QCD) phase transition. This model utilizes a discrete variable representing spin states, analogous to quark configurations, and incorporates a ‘Complex External Field’ term which mathematically mirrors the effect of the quark determinant in QCD. This determinant, crucial in QCD calculations, introduces complexities that often hinder direct numerical simulations. By employing the Potts model with this analogous field, researchers can investigate key features of the QCD phase transition – specifically the behavior near the critical point – in a computationally tractable system. The discrete nature of the Potts model avoids some of the challenges associated with continuous field theories, allowing for detailed analysis of the transition between hadronic and quark-gluon plasma phases.
The Tensor Renormalization Group (TRG) method provides an efficient numerical approach to analyze the three-dimensional Potts model by iteratively coarse-graining the tensor network representing the system. This technique circumvents the “sign problem” inherent in direct Quantum Chromodynamics (QCD) simulations, which arises from the oscillatory nature of the fermion determinant. TRG achieves this by working with a positive-definite tensor network, effectively summing over all possible configurations without encountering cancellations that lead to exponentially increasing statistical errors. Consequently, TRG enables the study of phase transitions in the Potts model – a simplified analogue of the QCD phase transition – with significantly reduced computational cost and improved statistical precision compared to methods susceptible to the sign problem.
Numerical analysis of the three-state Potts model, utilizing Binder cumulant analysis and scaling relations, determined a critical point (C_c) of 1.195 x 10-4. Further investigation revealed a transition back to first-order behavior at increased densities, indicated by a critical point of [1.195(7)]-1 x 104. The value in parentheses represents the estimated statistical uncertainty associated with the determination of this second critical point, providing a quantitative measure of the precision achieved in the analysis.
Universality and Implications: When Simplicity Reveals Truth
The three-dimensional three-state Potts model, a statistical mechanics system used to model magnetic materials and other phenomena, exhibits a specific type of critical behavior classified as belonging to the Ising Universality Class. This categorization signifies that, despite the model’s specific details – three internal states instead of the simpler two of the Ising model – its behavior near the critical point is fundamentally the same as a wide range of other physical systems. This means properties like the critical exponents – which describe how quantities change near the transition – are identical to those found in systems as diverse as binary alloys and liquid-gas transitions. Determining this universality class is crucial because it allows physicists to apply insights gained from simpler, well-understood models to more complex systems, reducing the need for exhaustive calculations for each new scenario. The finding, confirmed through meticulous Binder cumulant analysis yielding B_4c = 1.601(6), demonstrates a deep connection between seemingly disparate physical systems and provides a powerful tool for understanding phase transitions in nature.
Confirmation of the critical behavior relies on Binder cumulant analysis, a technique sensitive to the underlying universality class of a phase transition. This analysis yielded a value of B_4c = 1.601(6), a dimensionless ratio that serves as a fingerprint identifying membership within the Ising Universality Class. Significantly, this result implies that the quantum chromodynamics (QCD) phase transition, occurring at high densities and with heavy quark masses, demonstrates the same universal characteristics-meaning its critical properties are independent of the specific microscopic details of the strong force. This universality is a powerful simplification, suggesting a shared underlying structure governing diverse physical systems and offering a pathway to predict the behavior of dense matter found in extreme astrophysical environments, such as neutron star mergers.
The identification of universal behavior in the three-dimensional Potts model extends beyond theoretical physics, offering a powerful lens through which to examine matter under the most extreme conditions. This universality suggests that the properties of dense matter, such as that found within neutron stars, are not uniquely determined by the complex interactions between quarks and gluons, but rather governed by a smaller set of fundamental principles. Consequently, insights gained from studying relatively simple models – like the Potts model – can directly inform our understanding of phenomena such as neutron star mergers and the equation of state of matter at ultra-high densities. Predicting the behavior of matter in these environments is crucial for interpreting observational data from gravitational wave detectors and electromagnetic telescopes, ultimately allowing scientists to probe the fundamental nature of strong interactions and the structure of matter itself.
The pursuit of elegant phase diagrams, as demonstrated by this investigation into high-density QCD, inevitably courts disappointment. The researchers map a complex transition – first-order, then crossover, then again first-order – a beautifully intricate structure destined to be stressed by the realities of tensor renormalization group calculations. It echoes a familiar pattern: models, even those grounded in effective theory, struggle against the chaotic edge cases of true quark matter. As Paul Feyerabend observed, “Anything goes.” The insistence on a definitive, universally applicable ‘phase structure’ feels optimistic, given the inherent limitations of approximating extreme conditions. This paper, though rigorous, simply refines the tools of structured panic; a detailed map for when, not if, the elegant theory breaks down.
Beyond the Diagram
The mapping to a three-state Potts model, while elegant, merely shifts the complexity. The observed re-entrant behavior – first-order, then crossover, then first-order again – is intriguing, yet begs the question of what underlying physics necessitates such a convoluted transition scheme. It is a pattern destined to be smoothed over by numerical approximations, and ultimately justified post hoc. The true test will not be reproducing the phase boundaries, but predicting observables in regimes inaccessible to current simulations-a feat rarely achieved, and even more rarely surprising.
The application of tensor renormalization group techniques is, predictably, limited by computational resources. Each refinement of the lattice spacing, each increase in volume, will reveal a new source of systematic error, a new scale at which the effective theory breaks down. The pursuit of ‘infinite volume’ and ‘zero lattice spacing’ is a familiar, Sisyphean task. One suspects the most interesting physics resides precisely at those inaccessible scales, lurking beyond the reach of any tractable model.
Future work will undoubtedly focus on incorporating more ‘realistic’ features-finite temperature effects, dynamical quarks, perhaps even non-equilibrium dynamics. Each addition will increase the model’s complexity, but also its opacity. The core challenge remains: to extract universal behavior from a system inherently sensitive to microscopic details. It is a pursuit fraught with peril, but one that, inevitably, will continue. After all, if all tests pass, it’s because they test nothing.
Original article: https://arxiv.org/pdf/2601.15720.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- How to Unlock the Mines in Cookie Run: Kingdom
- Assassin’s Creed Black Flag Remake: What Happens in Mary Read’s Cut Content
- Jujutsu Kaisen: Divine General Mahoraga Vs Dabura, Explained
- Upload Labs: Beginner Tips & Tricks
- Where to Find Prescription in Where Winds Meet (Raw Leaf Porridge Quest)
- The Winter Floating Festival Event Puzzles In DDV
- Top 8 UFC 5 Perks Every Fighter Should Use
- How to Use the X-Ray in Quarantine Zone The Last Check
- Xbox Game Pass Officially Adds Its 6th and 7th Titles of January 2026
- Jujutsu: Zero Codes (December 2025)
2026-01-24 12:23