Author: Denis Avetisyan
A new coding scheme, Partially Polarized Polar (PPP) codes, promises to enhance the reliability and efficiency of data transmission in next-generation wireless networks.
This review details PPP codes, a novel inter-segment coding approach that recovers performance lost in segmented polar codes without increasing hardware complexity, offering improved blind decoding for 5G/6G systems.
Achieving robust and efficient communication in rapidly evolving wireless standards like 6G presents a continual challenge, particularly for downlink control channels demanding low-latency and reliable decoding of multiple candidates. This paper introduces a novel coding scheme, Partially Polarized Polar (PPP) codes, detailed in ‘Partially Polarized Polar Codes: A New Design for 6G Control Channels’, which strategically modifies conventional polar codes to enhance early termination capabilities. By selectively pruning polarization kernels, PPP codes recover performance lost in segmented approaches without increasing hardware complexity, offering substantial gains at larger block lengths. Could this innovative design unlock improved efficiency and reduced latency for future wireless communication systems?
The Foundation of Reliable 5G: Polar Codes and the Challenge of Complexity
The foundation of reliable communication in 5G New Radio (NR) hinges on the implementation of polar codes for transmitting Downlink Control Information (DCI). Unlike earlier coding schemes, polar codes approach the Shannon limit – the theoretical maximum data transmission rate – offering exceptional error correction capabilities even in challenging radio conditions. This is achieved through a construction process that creates ‘good’ and ‘bad’ code branches, concentrating the information on the more reliable branches to minimize decoding errors. Consequently, polar codes ensure the critical control signals – directing devices how to interpret incoming data – reach their destination accurately, even amidst interference and noise. The robustness of this method is vital for maintaining consistent connectivity and performance in the complex 5G network architecture, enabling features like beamforming and efficient resource allocation.
The transmission of Downlink Control Information (DCI) in 5G New Radio (NR) utilizes polar codes for reliability, but decoding this information, delivered via the Physical Downlink Control Channel (PDCCH), introduces substantial computational demands on user devices. This complexity arises from the iterative nature of polar decoding algorithms, requiring numerous calculations to correct potential errors in the received signal. As 5G advances and future systems like 6G anticipate even greater volumes of control signaling-necessary for features like massive MIMO and ultra-reliable low-latency communication-the burden on device processing capabilities intensifies. Effectively managing this decoding complexity is therefore critical, not only for ensuring dependable 5G performance but also for paving the way for the energy-efficient and scalable communication systems of tomorrow.
The escalating demands placed on wireless communication networks necessitate increasingly efficient decoding methods for control signaling. As systems evolve beyond 5G towards 6G and beyond, the volume and complexity of Downlink Control Information (DCI) – essential for coordinating device operation – are projected to rise dramatically. This growth isn’t merely quantitative; future systems will likely incorporate more sophisticated features, requiring more detailed and frequent control exchanges. Consequently, the ability of user equipment to decode these signals quickly and reliably becomes paramount, directly impacting network capacity, latency, and overall performance. Without advancements in decoding efficiency, the potential benefits of future wireless technologies could be significantly hampered, as devices struggle to keep pace with the increased signaling load and the stringent requirements of emerging applications.
Beyond Independent Blocks: Inter-Segment Coding for Enhanced Reliability
Inter-segment coding deviates from traditional error correction schemes by intentionally introducing dependencies between distinct segments of a transmitted payload. This contrasts with independent block coding where each segment is encoded and decoded in isolation. By leveraging these interdependencies, the coding process can exploit redundancy across segments, leading to improved coding gains – a reduction in the required resources to achieve a target error rate. Furthermore, this approach enhances reliability as the decoding of one segment can be aided by information derived from other segments, mitigating the impact of errors and potentially improving the overall system’s ability to recover corrupted data. The degree of dependency and the specific method used to establish it determine the magnitude of these gains and the complexity of the decoding process.
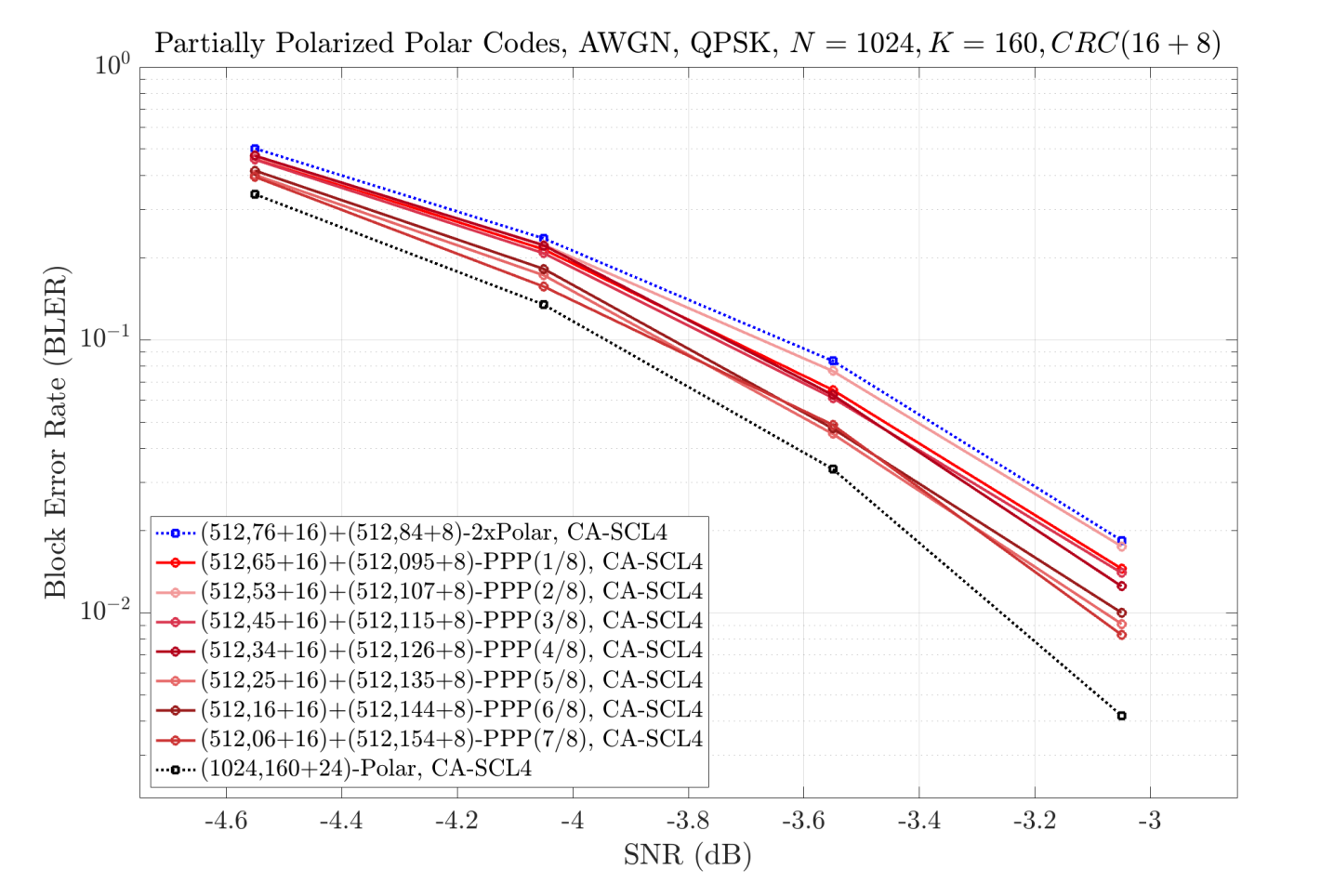
Partial Polarization represents a pragmatic approach to inter-segment coding by selectively polarizing a subset of the information bits, rather than attempting full polarization of all bits. This method achieves a balance between coding performance and computational complexity; full polarization, while optimal, demands significant encoding and decoding resources. By limiting the polarization process to specific, strategically chosen bits – often those most critical for reliable communication – Partial Polarization reduces the number of N values required for the Polar Code construction, thereby decreasing complexity. The resulting code maintains a substantial portion of the performance gains offered by full Polar Codes, while significantly simplifying implementation, particularly in resource-constrained environments.
Inter-segment coding techniques, such as Partial Polarization, build upon the foundation of Polar Codes to improve the reliability and spectral efficiency of control signaling. Polar Codes, while offering performance close to the Shannon limit, can be further optimized by introducing dependencies between independently encoded segments. This allows for joint decoding, effectively increasing the code length and reducing the frame error rate, particularly for short block lengths common in control channels. The resultant gains are achieved without fundamentally altering the Polar Code structure, maintaining compatibility with existing decoding algorithms while improving overall system performance and enabling higher data rates for control information.
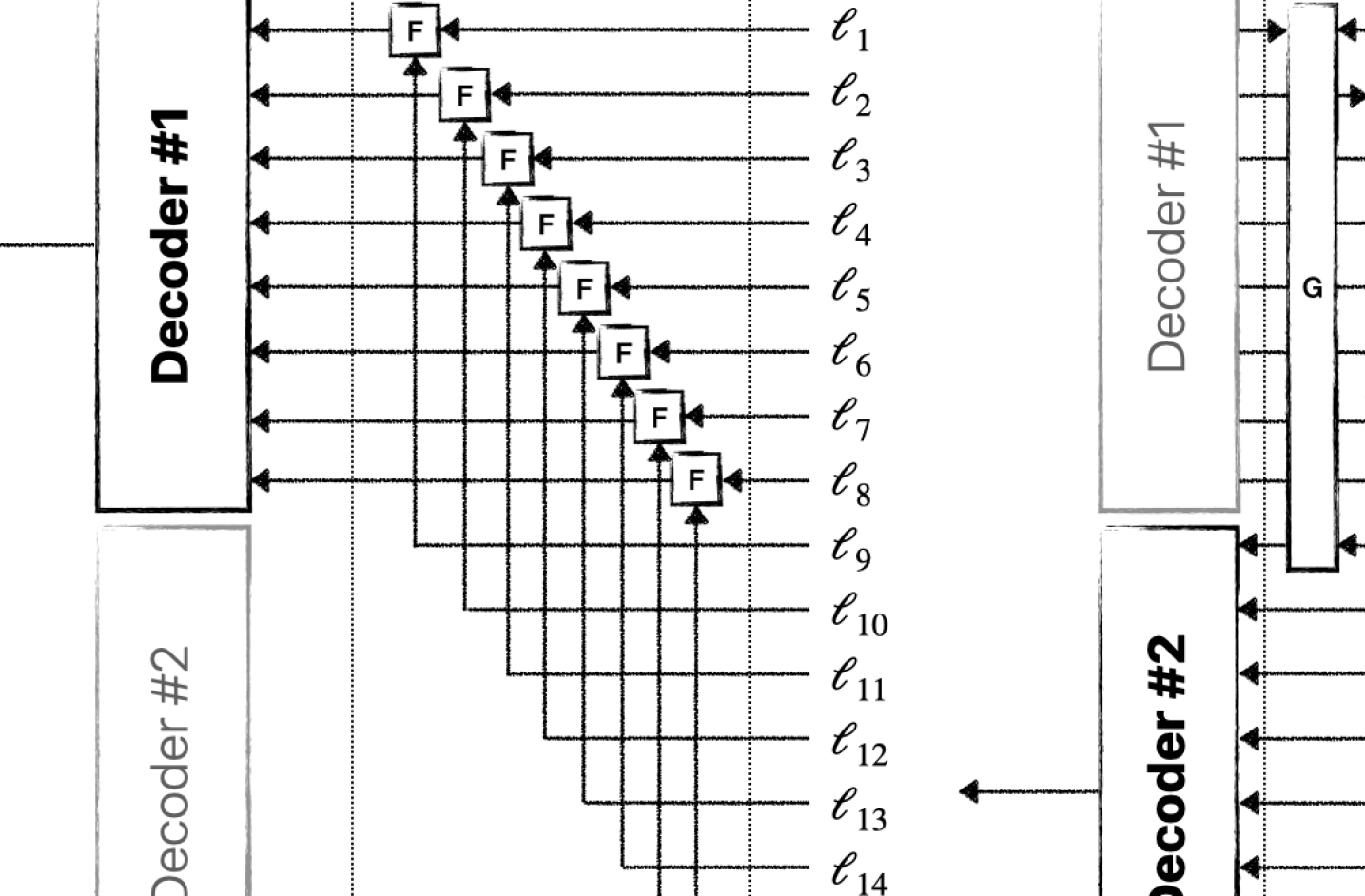
Accelerating Control Signal Recovery: Innovations in Decoding Strategies
Two-Stage Decoding is an optimization technique for polar codes that reduces computational complexity by terminating the decoding process as soon as sufficient information regarding the transmitted data is recovered. Traditional decoding algorithms typically proceed through a fixed number of stages, regardless of whether early stages have already yielded reliable estimates of the information bits. In contrast, Two-Stage Decoding monitors the reliability of the decoded bits during each stage and halts processing when a predetermined confidence level is reached. This early termination significantly lowers the average number of decoding operations, resulting in reduced latency and power consumption, particularly for high signal-to-noise ratio (SNR) scenarios where information can be reliably extracted with fewer iterations.
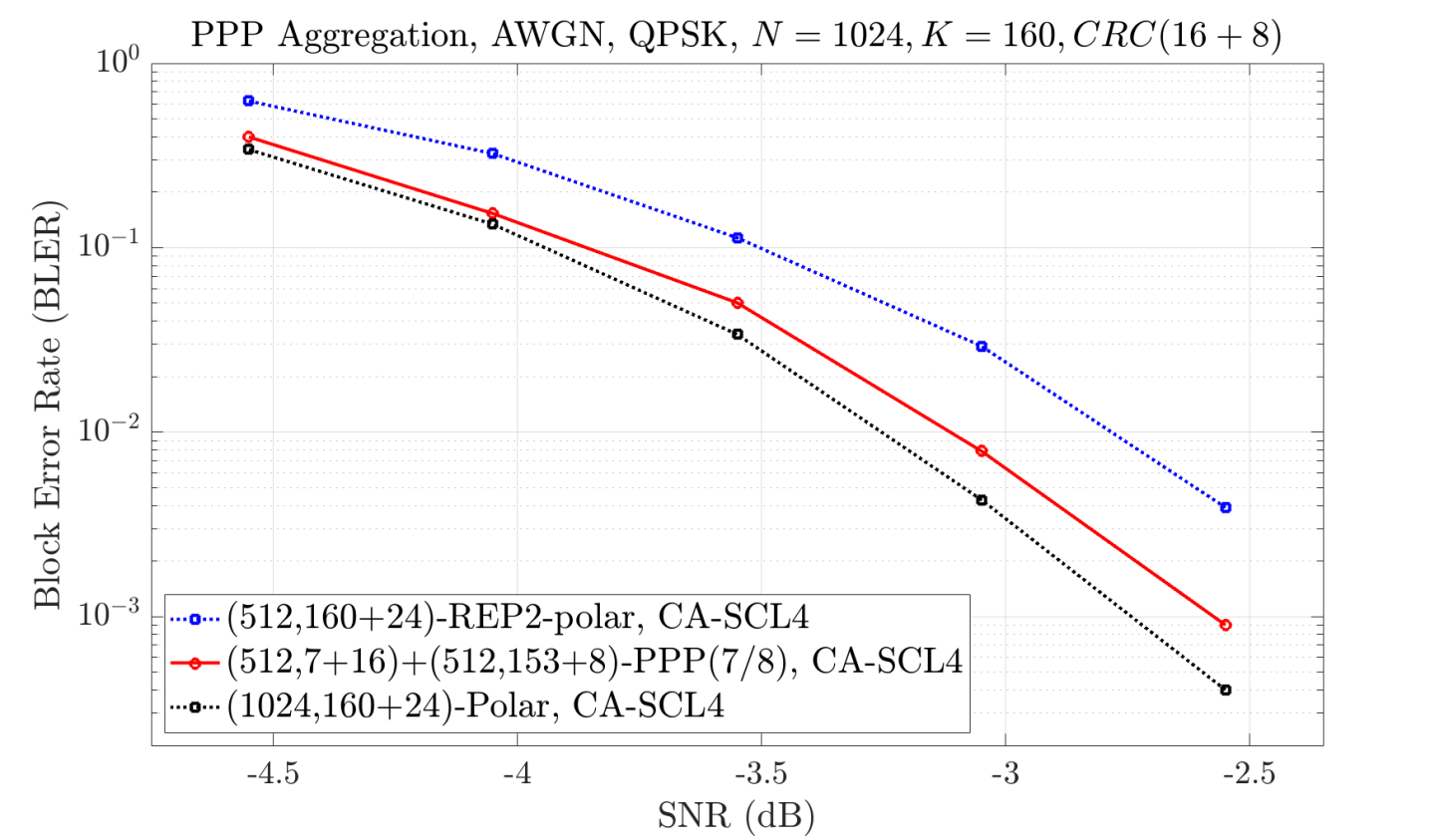
PPP (Partial Polarization with Two-Stage Decoding) codes represent an optimization technique for polar codes that aims to enhance performance without increasing hardware complexity. These codes combine partial polarization, a method of constructing codes with specific properties, with two-stage decoding, which allows for early termination of the decoding process when sufficient information is recovered. Crucially, PPP codes leverage frozen bits – predetermined bits with known values – to streamline the decoding process and improve error correction capabilities. Performance evaluations, specifically with code lengths of N=512 and N=1024 and payload size K=160, demonstrate that PPP codes achieve performance levels comparable to longer polar codes while maintaining the hardware complexity of shorter codes.
Performance evaluations utilizing code lengths of 512 and 1024 bits with a payload size of 160 bits demonstrate the superior performance of Partial Polarization with Two-Stage Decoding (PPP) codes compared to traditional segmentation and aggregation methods. These tests indicate a quantifiable improvement in signal recovery and reduced error rates when employing PPP codes under the specified conditions. The observed gains are attributable to the efficient decoding process and optimized code structure of PPP, allowing for more accurate and faster recovery of the transmitted payload compared to the alternatives.
Segmentation of a data payload for transmission introduces a signal-to-noise ratio (SNR) degradation typically ranging from 0.3 to 0.5 dB. This performance loss is a consequence of the added overhead and complexity associated with dividing and reassembling the data stream. However, the implementation of Partial Polarization with Two-Stage Decoding (PPP) codes effectively mitigates this SNR degradation. PPP codes, by combining partial polarization techniques with optimized decoding strategies and frozen bits, recover a substantial portion of the lost SNR, resulting in performance comparable to that of longer polar codes without increasing hardware complexity.
Successive Cancellation List Decoding (SCLD) is a decoding algorithm used with Polar codes to enhance reliability by maintaining a list of the most probable code word candidates at each decoding step. Unlike standard Successive Cancellation (SC) decoding which selects a single path, SCLD explores multiple potential solutions in parallel, effectively mitigating the impact of erroneous decisions made early in the process. The list size, denoted as L, controls the trade-off between decoding complexity and accuracy; larger values of L increase the probability of containing the correct code word, but also increase computational demands. This technique is particularly beneficial in scenarios with low Signal-to-Noise Ratios (SNR) or in environments prone to interference, where the likelihood of decoding errors is higher, and provides a significant performance gain compared to the basic SC decoder.
Adaptive Optimization: Harnessing Reinforcement Learning for Dynamic Code Design
Polarization-preserving photonic (PPP) codes, crucial for reliable data transmission, often face performance limitations as channel conditions fluctuate. Recent research demonstrates the potential of reinforcement learning (RL) to address this challenge by dynamically optimizing these codes. Instead of relying on pre-defined code parameters, an RL agent learns to adapt the code’s structure in real-time, responding to variations in signal strength, interference, and noise. This adaptive approach allows the system to consistently maintain high throughput and low error rates, even in highly dynamic and unpredictable environments. The agent explores different code configurations, receiving feedback – a ‘reward’ – based on transmission performance, and iteratively refines its strategy to maximize this reward. This effectively transforms the code design process from a static configuration to a continuous optimization loop, significantly enhancing the resilience and efficiency of photonic communication systems.
The complex design space of Polar codes presents a significant challenge for traditional optimization methods; however, Graph Neural Networks (GNNs) offer a powerful approach to navigate this landscape within a reinforcement learning framework. GNNs excel at representing and analyzing the structural relationships inherent in these codes, treating the code’s constituent blocks and their interconnections as nodes and edges in a graph. This allows the RL agent to learn a nuanced understanding of how specific code parameters – such as the rate of each block or the chosen construction method – impact overall performance. By encoding the code’s architecture as a graph, the GNN effectively extracts meaningful features that guide the RL agent’s exploration, enabling it to identify optimal code configurations far more efficiently than through random search or exhaustive evaluation. This combination unlocks the potential for dynamic code adaptation, tailoring the code’s structure to the specific demands of the communication channel and maximizing data transmission reliability.
Adaptive code design, leveraging reinforcement learning, offers a dynamic solution to the challenges of fluctuating communication channels. This approach centers on ‘capacity re-balancing’, a process where code parameters are intelligently adjusted to maintain optimal performance, even when signal strength is compromised. Through iterative learning, the system identifies how to modify coding schemes – such as altering redundancy or modulation techniques – to maximize data throughput while simultaneously minimizing the incidence of transmission errors. Crucially, this isn’t a pre-programmed response to specific SNR levels; instead, the RL agent learns to anticipate channel behavior and proactively reshape the code for resilience. This is particularly impactful in low-SNR environments, where traditional, static codes often falter, leading to unreliable communication. By continuously refining its strategy based on observed performance, the system achieves robust and efficient data transmission, effectively ‘re-balancing’ capacity to match the prevailing conditions.
The pursuit of efficient coding schemes, as demonstrated by Partially Polarized Polar (PPP) codes, echoes a fundamental tenet of system design: optimization arises not from complexity, but from elegant simplicity. These codes attempt to recover lost gains in segmented polar codes, improving blind decoding performance without escalating hardware demands-a deliberate effort to maintain a balanced architecture. As Donald Knuth observed, “Premature optimization is the root of all evil,” and the PPP approach suggests a mindful refinement, focusing on structural improvements to achieve gains, rather than layering on unnecessary complexity. Good architecture is invisible until it breaks, and only then is the true cost of decisions visible.
What Lies Ahead?
The introduction of Partially Polarized Polar (PPP) codes represents a considered step toward reclaiming efficiency lost in the pursuit of segmented designs. Yet, elegance is rarely found in isolated improvements. The true measure of this approach will not be simply in benchmark gains, but in how it interacts with the broader system architecture. Current analyses largely treat the channel as a static entity; a realistic evaluation demands scrutiny under dynamic conditions, particularly concerning feedback latency and imperfect channel state information. The promise of blind detection is compelling, but relies on a delicate balance – any disruption to this equilibrium could swiftly diminish performance.
A crucial area for further exploration lies in the adaptability of these codes. While current implementations demonstrate gains for specific scenarios, the capacity to dynamically adjust polarization profiles based on channel characteristics remains largely untapped. The scalability of such adaptations is paramount; clever algorithms will be favored over brute-force computational power. A truly robust system must anticipate, not merely react to, the inherent unpredictability of the wireless environment.
Ultimately, the value of PPP codes will reside in their integration with other advancements. The ecosystem of 6G – massive MIMO, intelligent reflecting surfaces, and terahertz communication – will either amplify or negate their benefits. The challenge is not merely to optimize the code itself, but to understand its role within a complex, evolving network. The simplicity of the initial concept must be preserved, lest it become another layer of complication in an already intricate system.
Original article: https://arxiv.org/pdf/2601.15404.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- How to Unlock the Mines in Cookie Run: Kingdom
- Assassin’s Creed Black Flag Remake: What Happens in Mary Read’s Cut Content
- Jujutsu Kaisen: Divine General Mahoraga Vs Dabura, Explained
- The Winter Floating Festival Event Puzzles In DDV
- Upload Labs: Beginner Tips & Tricks
- Top 8 UFC 5 Perks Every Fighter Should Use
- Jujutsu: Zero Codes (December 2025)
- Where to Find Prescription in Where Winds Meet (Raw Leaf Porridge Quest)
- MIO: Memories In Orbit Interactive Map
- Xbox Game Pass Officially Adds Its 6th and 7th Titles of January 2026
2026-01-25 15:21