Author: Denis Avetisyan
New calculations refine our understanding of how B mesons decay into leptons, improving the accuracy of tests for new physics.
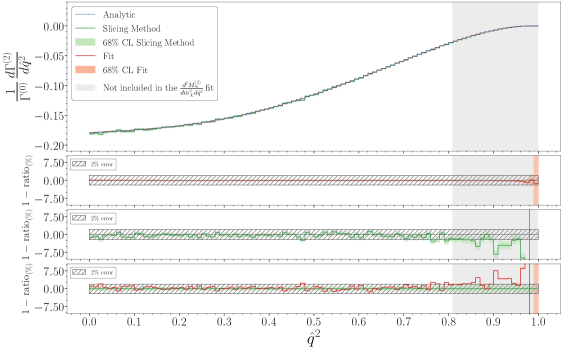
This work presents a semi-analytic method for calculating Next-to-Next-to-Leading Order corrections to structure functions in the inclusive semileptonic decay of b quarks.
Precise theoretical predictions for heavy quark decays are challenged by the complexity of higher-order perturbative corrections. This paper, ‘Structure functions for the inclusive semileptonic $b$-quark decay at NNLO: a semi-analytic calculation’, presents a novel approach to compute Next-to-Next-to-Leading Order (NNLO) corrections to the structure functions governing the inclusive semileptonic decay of $b$ quarks, utilizing a combination of analytic results from Heavy Quark Effective Theory and a phase-space slicing Monte Carlo integration. This semi-analytic method yields structure functions in excellent agreement with existing results and provides a robust framework for calculating kinematic distributions and moments. Will this approach pave the way for even more accurate predictions in flavor physics and beyond?
The Mathematical Imperative of Precision in Flavor Physics
The precise determination of the Cabibbo-Kobayashi-Maskawa (CKM) matrix element |V_{ub}| stands as a pivotal test of the Standard Model of particle physics. This parameter governs the rate of certain particle decays and, if measured with sufficient accuracy, can reveal subtle discrepancies hinting at new physics beyond our current understanding. Any deviation from the Standard Model prediction for |V_{ub}| could signify the presence of undiscovered particles or interactions, offering a crucial pathway to resolving long-standing mysteries in particle physics, such as the matter-antimatter asymmetry in the universe. Consequently, significant effort is dedicated to refining both theoretical calculations and experimental measurements of this fundamental quantity, pushing the boundaries of precision in flavor physics.
Determining the value of |V_{ub}|, a key parameter within the Standard Model of particle physics, has historically presented a significant challenge due to the reliance on approximations in conventional calculation methods. These methods often involve modeling complex interactions between quarks and gluons – collectively known as hadronic dynamics – which are inherently difficult to predict with precision. Consequently, estimations of |V_{ub}| are frequently plagued by substantial theoretical uncertainties, limiting the ability to rigorously test the Standard Model and search for deviations that might signal the presence of new physics. The challenge lies not in the fundamental principles themselves, but in the intricacies of accurately representing the strong force interactions governing the behavior of quarks within hadrons, necessitating innovative approaches and refinements to existing techniques.
Determining |V_{ub}| with precision demands a nuanced comprehension of hadronic dynamics – the complex interactions governing the behavior of quarks and gluons within composite particles like mesons and baryons. These interactions are not easily predicted by the fundamental theory of the Standard Model, requiring physicists to employ sophisticated modeling techniques and approximations. The challenge arises from the inherent complexity of the strong force, which binds quarks together, and the multitude of possible configurations these particles can adopt. Consequently, calculations involving hadronic dynamics are often plagued by substantial theoretical uncertainties, necessitating continuous refinement of models and a rigorous assessment of their limitations. Improved understanding of these dynamics is therefore central to unlocking the full potential of |V_{ub}| measurements as a sensitive probe for new physics beyond the Standard Model.
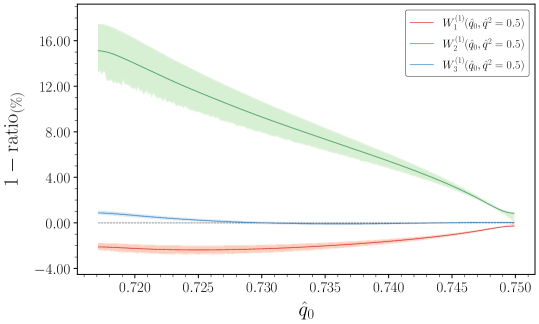
Deconstructing Decay Rates: The Operator Product Expansion
The Operator Product Expansion (OPE) is a technique used in quantum field theory to calculate decay rates by expressing them as a series of terms involving operators with increasing dimensionality. Crucially, OPE allows for the separation of short-distance (perturbative) and long-distance (non-perturbative) contributions. The decay rate, typically represented as Γ, is then expressed as a sum of terms where each term involves a local operator product and a corresponding Wilson coefficient. These Wilson coefficients are calculable through perturbation theory, while the non-perturbative contributions are encoded in matrix elements of the local operators between the initial and final states, often referred to as shape functions. By systematically including higher-dimensional operators, the OPE provides a controlled expansion allowing for increasingly precise calculations of decay rates even when strong interactions dominate, as is frequently the case in heavy quark decays.
The Operator Product Expansion necessitates a precise understanding of shape functions, also known as distribution amplitudes, to accurately model the internal structure of the B meson. These functions describe the probability amplitude of finding the constituent quarks within the meson, parameterized by their momentum fractions and transverse momenta. Since the B meson is a composite particle, its decay rate is sensitive to these internal dynamics; therefore, accurate predictions from the OPE depend directly on the correct form of the shape functions. These functions are typically non-perturbative objects, meaning their determination requires methods beyond standard perturbation theory, often involving lattice QCD calculations or phenomenological modeling constrained by experimental data.
Heavy Quark Effective Theory (HQET) and Soft-Collinear Effective Theory (SCET) represent advancements in refining the Operator Product Expansion (OPE) for calculations in decay rates. HQET simplifies calculations by exploiting the mass hierarchy between the heavy quark and other scales, allowing for systematic treatment of power corrections related to \Lambda_{QCD} . SCET focuses on isolating the dynamics at long distances and soft momentum transfers, providing a framework to calculate non-perturbative contributions with improved accuracy and control over factorization ambiguities. Both theories utilize factorization theorems and renormalization group techniques to organize perturbative and non-perturbative effects, enabling precise predictions for observables sensitive to non-perturbative dynamics and reducing reliance on phenomenological models.
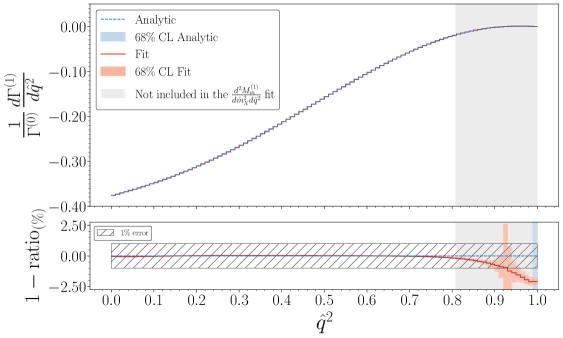
Constraining the Unknown: Modeling Shape Functions with Rigor
Model-independent parameterizations of shape functions are crucial for ensuring the reliability of decay rate calculations without reliance on specific theoretical assumptions. Methods such as SIMBA and NNVub achieve this by employing a flexible, data-driven approach to represent the underlying non-perturbative dynamics. These techniques typically involve a basis of functions-often polynomials or splines-fitted to experimental data or theoretical constraints, allowing for a representation of the shape function without imposing a pre-defined functional form. The resulting parameterizations are then used within perturbative calculations to evaluate observables, minimizing the impact of model-dependent uncertainties and enhancing the overall predictive power of the analysis.
Infrared divergences arise in calculations of decay rates due to the emission of soft or collinear particles, leading to logarithmic integrals that render perturbative calculations unstable. These divergences are not physical and require regularization and renormalization techniques for their proper treatment. The Slicing Method, employed within Parton-Level Monte Carlo simulations, addresses this by introducing a parameter, Δ, which defines a minimum transverse momentum scale for emitted partons; effectively, it separates the soft and collinear regions of phase space. By integrating over a finite range of transverse momenta, the method avoids the singularities associated with zero transverse momentum, providing a finite, albeit parameter-dependent, result. The physical result is then obtained by extrapolating to \Delta \rightarrow 0 and absorbing the associated logarithmic terms into the overall renormalization scheme.
Next-to-Next-to-Leading Order (NNLO) calculations represent a high-order perturbative approach to determining the decay rate, incorporating radiative corrections up to O(\alpha_s^2). To further refine the accuracy and address potential issues with fixed-order perturbation theory, these NNLO calculations are augmented with Broadening-Leading-Momentum (BLM) corrections. BLM rescaling modifies the momentum-space integration variables to improve the convergence of the perturbative series and reduce sensitivity to the arbitrary factorization scale. Validation of this combined NNLO+BLM approach demonstrates quantitative agreement with Next-to-Leading Order (NLO) analytic results, typically achieving concordance within a 1-2% margin, indicating a robust and precise determination of the decay rate.
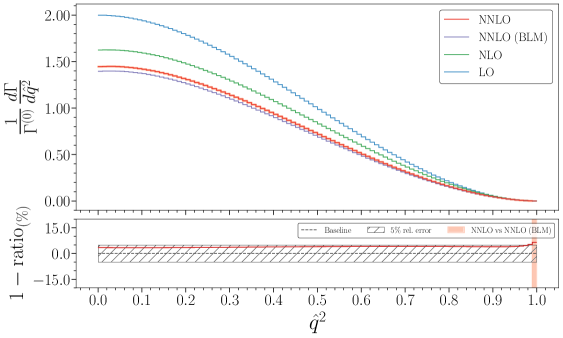
Experimental Scrutiny and the Path Forward for |Vub|
The Belle II experiment, currently operating at the SuperKEKB collider, is systematically accumulating an unprecedented dataset crucial for precision measurements of the |V_{ub}| parameter-a key element in understanding the Cabibbo-Kobayashi-Maskawa (CKM) matrix. This ongoing data collection isn’t simply about quantity; it’s designed to dramatically reduce the statistical uncertainties that have historically plagued determinations of |V_{ub}|. By observing the decay of B mesons into various final states, physicists can extract the value of |V_{ub}| with increasing accuracy. The sheer volume of data-orders of magnitude greater than previous experiments-allows for more robust statistical analyses and the potential to reveal subtle effects previously hidden within experimental noise, ultimately contributing to a more complete test of the Standard Model of particle physics.
The pursuit of a precise determination of the |V_{ub}| parameter, crucial for understanding the dynamics of the Standard Model, relies heavily on the collaborative efforts of the particle physics community. The Heavy Flavour Averaging Group (HFLAV) plays a vital role by meticulously combining results obtained from multiple experiments, most notably the Belle II collaboration which is currently accumulating a substantial dataset. This synthesis isn’t simply an averaging of values; HFLAV employs rigorous statistical methods to account for systematic uncertainties and correlations between measurements from different experimental setups. The resulting global average for |V_{ub}| benefits from the combined statistical power of these experiments, significantly reducing uncertainties and providing a more robust foundation for theoretical comparisons and searches for physics beyond the Standard Model. This collaborative approach ensures the most accurate and reliable determination of this fundamental parameter currently available.
Precision measurements of the |V_{ub}| parameter rely not only on experimental data from facilities like Belle II, but also on sophisticated theoretical frameworks used to interpret those results. Approaches such as the BaBar-Belle Loop Normalization Procedure (BLNP), the GGS-based Optimized Universal (GGOU) scheme, and the Dual Gauge Evolution (DGE) framework provide the necessary tools to relate observed decay rates to fundamental parameters within the Standard Model. These frameworks account for complex effects like non-perturbative QCD corrections and radiative effects, allowing physicists to extract |V_{ub}| with improved accuracy. By combining the predictive power of these theoretical calculations with the growing datasets from experiments, researchers are steadily refining our understanding of flavor physics and searching for potential discrepancies that could hint at new physics beyond the Standard Model.
Analysis reveals a strong consistency between calculations employing Next-to-Leading Order (NLO) structure functions and experimental data, as evidenced by the close fit within 68% Confidence Level (CL) bands; however, this precision should not be misinterpreted as a complete representation of the overall uncertainty. Specifically, investigations into W_2(1), a kinematic variable crucial for understanding particle interactions, have revealed deviations exceeding 1% at low q^2 values. This phenomenon arises from a diminishing prefactor within the double differential distributions, effectively amplifying subtle variations and demanding a more nuanced interpretation of the results; continued refinement of both theoretical models and experimental techniques is therefore essential to fully resolve these discrepancies and achieve a more comprehensive understanding of the underlying physics.
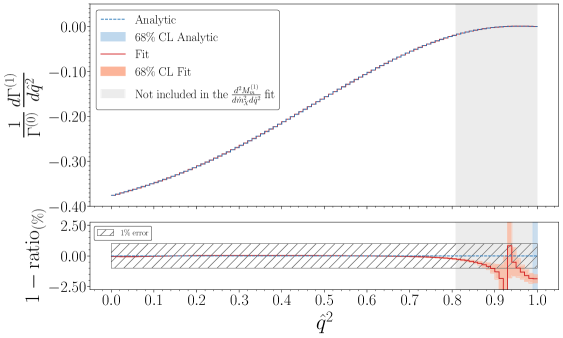
The pursuit of precise theoretical predictions, as demonstrated in this calculation of NNLO corrections to semileptonic decay structure functions, demands a relentless focus on eliminating ambiguity. The method’s hybrid approach-combining analytic rigor with Monte Carlo simulation-strives for a demonstrable truth, a provable result untainted by approximation. This echoes Søren Kierkegaard’s assertion: “Life can only be understood backwards; but it must be lived forwards.” Similarly, this work builds upon established theoretical foundations-the ‘past’ of particle physics-to move ‘forward’ and refine predictions with ever-increasing accuracy, ultimately aiming for an unassailable understanding of fundamental processes.
Beyond Perturbation
The pursuit of increasingly precise descriptions of semileptonic decay, as exemplified by this work’s NNLO calculation of structure functions, highlights a fundamental, if often unacknowledged, truth: precision without provability is merely an exercise in curve-fitting. The reliance on the Operator Product Expansion and Effective Field Theory, while yielding numerical improvements, does not address the underlying question of convergence. A finite order calculation, no matter how high, remains an approximation, and the implicit assumption of a well-behaved perturbative series requires continual, skeptical examination.
Future investigations must move beyond simply accumulating higher-order corrections. The true test lies in establishing rigorous error bounds, or, ideally, a non-perturbative framework that obviates the need for expansion altogether. Parton-level Monte Carlo integration, while a pragmatic necessity, should not be mistaken for a conceptual solution. It addresses the computational complexity, but not the inherent limitations of the perturbative approach.
One wonders if the field’s energies might be more fruitfully directed towards exploring alternative formalisms-perhaps those rooted in lattice gauge theory-that offer the potential for genuinely predictive power, rather than perpetually refining a system built upon assumptions. A truly elegant solution, after all, should not require ever-increasing computational resources to maintain its validity.
Original article: https://arxiv.org/pdf/2601.15447.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- How to Unlock the Mines in Cookie Run: Kingdom
- Assassin’s Creed Black Flag Remake: What Happens in Mary Read’s Cut Content
- Jujutsu Kaisen: Divine General Mahoraga Vs Dabura, Explained
- The Winter Floating Festival Event Puzzles In DDV
- Top 8 UFC 5 Perks Every Fighter Should Use
- Jujutsu: Zero Codes (December 2025)
- Upload Labs: Beginner Tips & Tricks
- Where to Find Prescription in Where Winds Meet (Raw Leaf Porridge Quest)
- MIO: Memories In Orbit Interactive Map
- Xbox Game Pass Officially Adds Its 6th and 7th Titles of January 2026
2026-01-25 18:38