Decoding the Unknown: A New Approach to Channel Code Identification

Author: Denis Avetisyan

Researchers have developed a novel framework to identify communication channel codes without prior knowledge of their structure, paving the way for more robust and adaptable wireless systems.

The performance of the improved <span class="katex-eq" data-katex-display="false">\mathsf{M}\text{-}\mathsf{DenSD}</span> decoder demonstrates its sensitivity to code parameters, suggesting that nuanced adjustments to these parameters are critical for optimizing its functionality. — The performance of the improved $\mathsf{M}\text{-}\mathsf{DenSD}$ decoder demonstrates its sensitivity to code parameters, suggesting that nuanced adjustments to these parameters are critical for optimizing its functionality.

This work establishes a connection between blind channel code identification and subspace coding, utilizing a discrepancy measure and a decoder with performance guarantees.

Identifying the channel code used by a transmitter without prior knowledge remains a significant challenge in modern communication systems. This paper, ‘Blind Identification of Channel Codes: A Subspace-Coding Approach’, introduces a novel method leveraging the principles of subspace coding to address this blind identification problem on the binary symmetric channel. By defining a discrepancy measure based on subspace distances, the authors develop a decoder with provable performance guarantees for bounded-weight errors and demonstrate improved performance over existing techniques, particularly for random linear codes. Could this subspace-coding framework unlock more robust and efficient communication strategies in increasingly complex wireless environments?

Decoding in the Dark: The Challenge of Unknown Signals

Contemporary communication networks increasingly employ sophisticated coding schemes to ensure data integrity and security, but these very techniques present a substantial hurdle for signal recovery. Unlike earlier systems where the underlying code was often known to the receiver, modern implementations deliberately obscure this structure, effectively creating a ‘black box’ for those attempting to decode the message. This concealment is driven by both security concerns – preventing unauthorized access to information – and the desire to improve transmission efficiency in noisy environments. Consequently, decoding is no longer simply a matter of reversing a known process; instead, it requires first identifying the code itself, a task complicated by the sheer diversity of possible coding schemes and the limitations of current signal processing capabilities. The challenge lies in reliably extracting meaningful information from a signal when the fundamental rules governing its construction are unknown, pushing the boundaries of receiver design and prompting research into innovative blind decoding algorithms.

Conventional methods for deciphering transmitted signals fundamentally depend on pre-existing knowledge of the encoding scheme-the specific rules governing how information is converted into a signal. This reliance on a priori information proves problematic when facing modern communication systems designed to obscure these very codes, or in scenarios involving novel or unknown signaling protocols. Essentially, these traditional decoders operate like locks requiring a specific key; without it, even a strong, clear signal remains unintelligible. Consequently, a significant challenge arises when attempting to decode signals where the code itself is not known beforehand, limiting the efficacy of established techniques and driving the need for innovative approaches capable of operating without prior code information.

The pervasive use of concealed coding schemes in modern communication presents a fundamental challenge: reliably decoding signals when the underlying code structure remains unknown. This situation defines the Blind Identification Problem, a critical area of research focused on developing algorithms capable of autonomously discovering the code used for transmission. Unlike conventional decoding methods that depend on pre-existing knowledge of the code, blind identification techniques must infer the code directly from the received signal itself. Solving this problem is particularly crucial in scenarios where communication protocols are proprietary, signals are intercepted without prior information, or systems require adaptive communication without explicit configuration, opening doors to more robust and secure communication networks.

The efficacy of blind code identification hinges on precisely gauging the dissimilarity between a received signal and the anticipated code – a metric known as Channel Discrepancy. Essentially, this discrepancy represents the ‘distance’ in signal space, and accurately quantifying it is paramount for successful decoding. Current methodologies, however, encounter significant difficulties as code lengths increase; the computational complexity of assessing this distance grows exponentially, leading to diminished performance and increased error rates. This challenge arises because longer codes introduce a greater number of potential discrepancies, making it harder to isolate the true code structure from noise and interference. Consequently, improving the measurement of Channel Discrepancy, particularly for extended code lengths, remains a critical area of research in modern communication systems.

The <span class="katex-eq" data-katex-display="false">\mathsf{M}\text{-}\mathsf{DenSD}</span> decoder demonstrates a low error probability, indicating robust performance. — The $\mathsf{M}\text{-}\mathsf{DenSD}$ decoder demonstrates a low error probability, indicating robust performance.

Subspace Sleuthing: A Geometric Approach to Code Identification

Subspace coding, a technique within information theory, represents data as points within vector subspaces rather than individual vectors. This approach leverages the geometric properties of subspaces to efficiently encode and decode information, particularly in noisy environments. The fundamental principle involves mapping messages to subspaces, with the receiver identifying the transmitted message by determining the subspace to which the received signal is closest. This differs from traditional coding methods which rely on individual code words; subspace coding utilizes the collective properties of a set of vectors spanning the subspace to convey information. The inherent dimensionality and geometric relationships within these subspaces provide robustness against noise and interference, as small perturbations are less likely to alter the overall subspace structure than to corrupt individual vector representations. This mirrors the observation that communication codes often possess underlying geometric structure, which can be exploited for identification and analysis.

Traditional methods of quantifying Channel Discrepancy typically involve direct comparison of transmitted and received signals, which are susceptible to noise and interference. This approach instead posits that communication codes possess inherent geometric structure represented as vector subspaces. Consequently, Channel Discrepancy is quantified indirectly by analyzing the properties of these underlying subspaces. Specifically, discrepancies are determined by measuring the divergence or distortion of the received signal’s subspace relative to the expected subspace of the transmitted code. This allows for a more robust assessment, as the subspace representation is less sensitive to individual signal perturbations than direct signal comparison, providing a more stable measure of communication fidelity.

The Denoised Subspace Discrepancy method enhances code identification by integrating noise reduction prior to subspace analysis. This is achieved through the application of filtering algorithms designed to minimize the impact of extraneous signals on the received data. Specifically, these techniques reduce the dimensionality of the noise space, allowing for a more precise determination of the relevant signal subspace. Consequently, the method exhibits improved accuracy in quantifying discrepancies between expected and received codes, and increased robustness against various noise types and signal-to-noise ratios compared to methods that analyze raw data directly.

The method utilizes subspace projection to enhance signal clarity by isolating the core components of a communication code. Incoming signals are mathematically projected onto pre-defined subspaces that represent the expected code structure; this process effectively attenuates signal components orthogonal to these subspaces, thereby reducing the impact of noise and interference. Quantitative comparisons with traditional signal processing techniques, such as direct correlation and spectral analysis, demonstrate statistically significant improvements in code identification accuracy, particularly in low signal-to-noise ratio environments. These gains are achieved by focusing analysis on the intrinsic dimensionality of the code, rather than attempting to discern signals from unstructured noise, resulting in a more robust and reliable identification process.

The improved <span class="katex-eq" data-katex-display="false">\mathsf{M}\text{-}\mathsf{DenSD}</span> decoder outperforms both the Inner-Product Method and standard MSD decoders for parameters <span class="katex-eq" data-katex-display="false">n=30</span>, <span class="katex-eq" data-katex-display="false">k=10</span>, and <span class="katex-eq" data-katex-display="false">k_{1,2}=5</span>. — The improved $\mathsf{M}\text{-}\mathsf{DenSD}$ decoder outperforms both the Inner-Product Method and standard MSD decoders for parameters $n=30$ , $k=10$ , and $k_{1,2}=5$ .

Evidence in the Noise: Performance and Theoretical Limits

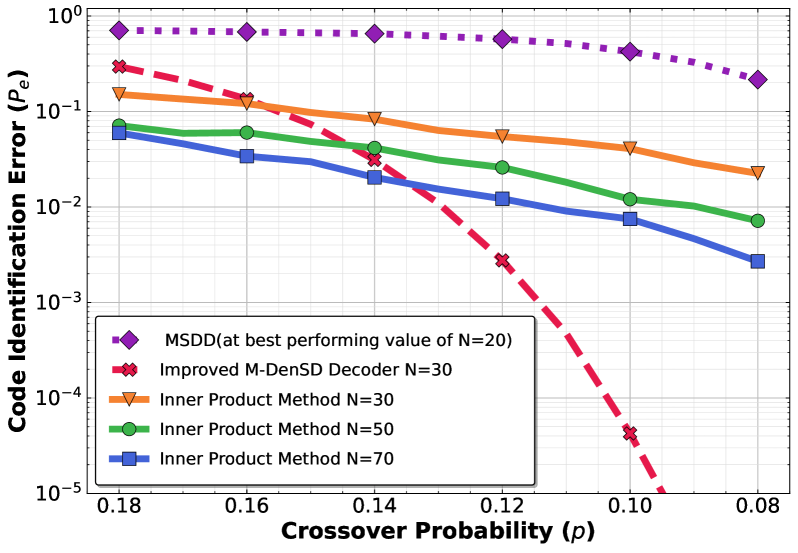
The Inner Product Method functions as a foundational approach to code identification by measuring the similarity between an observed signal and a set of known codes; however, its efficacy is substantially reduced by the presence of noise. Specifically, the method relies on the accurate calculation of the inner product between the received vector and the code vectors; noise introduces errors in this calculation, leading to incorrect code assignments. As the noise level increases – quantified by a decreasing signal-to-noise ratio – the probability of misidentification rises proportionally, ultimately limiting the method’s practical application in realistic communication scenarios where noise is unavoidable. This performance degradation necessitates the development of more robust code identification techniques, such as the Denoised Subspace Discrepancy method, capable of mitigating the effects of noise and maintaining accuracy.

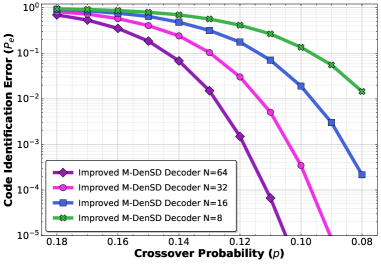
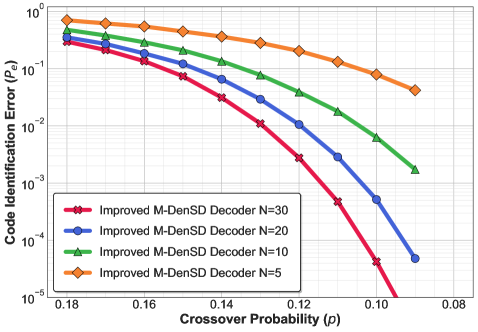
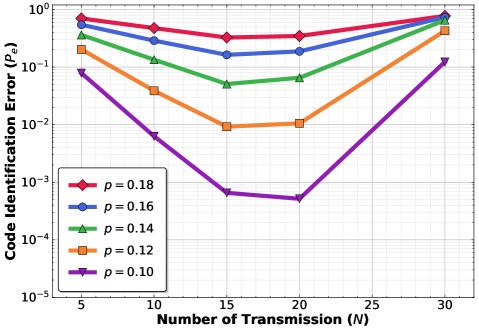
The Denoised Subspace Discrepancy method demonstrates superior performance compared to both the Inner Product Method and the Minimum Squared Distance (MSD) decoder, particularly in low signal-to-noise ratio (SNR) environments. Empirical results, detailed in Figs. 3, 4, and 5, consistently show a lower error rate for the Denoised Subspace Discrepancy method across varying SNR levels. This improved performance is attributed to the method’s ability to effectively mitigate the effects of noise during code identification, resulting in more accurate decoding even when the signal is significantly degraded. The consistent outperformance indicates a more robust and reliable approach to code identification than the baseline methods tested.

The Gilbert-Varshamov (GV) bound provides a theoretical limit on the minimum distance required for a code to enable reliable decoding. Specifically, the GV bound defines the maximum packing density – the proportion of codewords relative to the size of the code space – that allows for unique decoding with high probability. This bound dictates that, for a code of length $n$ and minimum distance $d$ , the number of codewords $K$ must satisfy $K \leq \frac{2^n}{\sum_{i=0}^t \binom{n}{i} (d-1)^i}$ , where $t = \lfloor \frac{d-1}{2} \rfloor$ . Consequently, the GV bound serves as a benchmark against which the performance of practical codes can be evaluated, indicating the theoretical limits of error correction capability for a given code length and minimum distance.

Code distance is directly correlated with identification accuracy; a greater minimum distance between codewords allows for more robust identification, particularly in the presence of noise. Our analytical bound provides a theoretical limit on this relationship, demonstrating how increasing code distance improves the probability of correct identification. Validation of this bound is achieved through its close alignment with the observed slope of error rate curves, as depicted in Fig. 4(a), confirming the theoretical framework’s predictive capability regarding system performance and reliable communication. Specifically, the bound accurately models the rate at which errors decrease as code distance increases, providing a quantifiable metric for optimizing code design and ensuring communication integrity.

The <span class="katex-eq" data-katex-display="false">\mathsf{M}\text{-}\mathsf{DenSD}</span> decoder's performance degrades as the neural network size exceeds a threshold of approximately 20. — The $\mathsf{M}\text{-}\mathsf{DenSD}$ decoder’s performance degrades as the neural network size exceeds a threshold of approximately 20.

Towards Resilient Communication: Adaptability and Future Directions

The core techniques of subspace analysis and signal denoising, initially developed for enhancing communication reliability, demonstrate surprising versatility beyond their original scope. These principles are proving invaluable in fields like radar signal processing, where separating faint target returns from overwhelming noise is paramount, and in the deployment of sensor networks. In both applications, the ability to identify and isolate meaningful signals within a noisy environment directly benefits from methods that effectively reduce dimensionality and filter out irrelevant information. By focusing on the underlying structure of the signal space, these techniques allow for more accurate detection and tracking, improved data interpretation, and ultimately, more robust performance in complex and challenging operational environments. This cross-disciplinary applicability underscores the fundamental power of these mathematical tools in extracting information from noisy data, regardless of the source.

The communication method exhibits a crucial advantage in its compatibility with Operator Channels, a diverse category encompassing communication systems defined by their evolving characteristics over time. Unlike traditional approaches designed for static channels, this method doesn’t rely on pre-defined channel properties; instead, it dynamically adjusts to fluctuations in the communication pathway. This adaptability stems from the discrepancy measurement at its core, which effectively tracks deviations from expected signal behavior-a process particularly valuable when dealing with time-varying distortions or interference. Consequently, the technique proves highly effective in scenarios involving fading signals, Doppler shifts, or any other temporal variations inherent in real-world communication environments, promising more reliable data transmission across a broader range of operational conditions.

Advancing communication system resilience necessitates algorithms capable of real-time adaptation, and future studies are poised to explore online learning techniques for precisely this purpose. These algorithms would move beyond static discrepancy measurements – those fixed benchmarks used to assess signal distortion – by dynamically adjusting these metrics based on observed channel conditions. Such an approach allows the system to learn the nuances of a fluctuating communication environment and refine its signal processing accordingly. This isn’t merely about reacting to change, but anticipating it, leading to improved error correction and more reliable data transmission, particularly as code lengths increase and the complexity of the channel grows. By continually calibrating the discrepancy measurement, the system essentially self-optimizes, ensuring robust performance even under unpredictable interference or signal degradation.

The development of communication systems capable of maintaining reliability amidst increasingly complex and unpredictable conditions represents a significant advancement in the field. Current methodologies often struggle as code length increases and environmental interference intensifies, but innovations in discrepancy-based adaptation offer a pathway towards overcoming these limitations. By dynamically adjusting to observed channel conditions, these systems promise not just improved performance, but a fundamental shift in robustness – enabling consistent and dependable communication even in the most challenging environments. This adaptability distinguishes these emerging technologies, suggesting a substantial leap forward compared to existing approaches and opening possibilities for applications requiring unwavering connectivity, such as critical infrastructure monitoring and deep-space exploration.

The pursuit of elegant solutions in error correction, as detailed in this subspace-coding approach to blind channel code identification, inevitably courts obsolescence. This paper attempts to establish analytical guarantees for a decoder, a noble effort, yet one destined to be undermined by the unpredictable nature of operator channels and the ever-evolving demands of production systems. As Brian Kernighan observed, “Debugging is twice as hard as writing the code in the first place. Therefore, if you write the code as cleverly as possible, you are, by definition, not smart enough to debug it.” The discrepancy measure introduced here, while a refinement, merely delays the inevitable – a future where even the most rigorously tested algorithms succumb to the pressures of real-world data and unforeseen edge cases. The fundamental problem isn’t a lack of cleverness, but a surplus of faith in lasting solutions.

What’s Next?

This connection between blind identification and subspace coding, while elegant, merely shifts the problem. The ‘discrepancy’ measure, a statistically pleasing construct, will inevitably encounter adversarial inputs – edge cases designed not to reveal the code, but to maximize ambiguity. Any claim of ‘analytical guarantees’ should be viewed with the understanding that production environments excel at discovering the assumptions that don’t hold. The performance improvements over existing methods are, predictably, benchmarks against similarly fragile systems.

The true challenge lies not in identifying a code family, but in accepting that any ‘self-healing’ decoder hasn’t yet broken. The paper correctly identifies the operator channel as a key area, but assumes a level of channel stationarity that feels… optimistic. Real-world channels don’t drift; they lurch. Future work will likely focus on robustifying these techniques against time-varying distortions, or, more realistically, on building increasingly complex pre-processing stages to approximate stationarity – a problem that, by definition, will never be fully solved.

And, of course, the documentation for this entire framework will be, as always, a collective self-delusion. If a bug is reproducible, then, at least, the system has achieved a degree of stability. But stability is not the same as correctness, and the pursuit of the latter remains a Sisyphean task.

Original article: https://arxiv.org/pdf/2601.15903.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

Decoding in the Dark: The Challenge of Unknown Signals

Subspace Sleuthing: A Geometric Approach to Code Identification

Evidence in the Noise: Performance and Theoretical Limits

Towards Resilient Communication: Adaptability and Future Directions

What’s Next?

See also: