Author: Denis Avetisyan
New research challenges the long-held assumption that strong stability preserving (SSP) methods are essential for maintaining numerical stability when solving hyperbolic conservation laws.
The study demonstrates that non-SSP Runge-Kutta methods can achieve stability under specific conditions, potentially broadening the range of viable numerical techniques.
Maintaining stability in numerical simulations of hyperbolic conservation laws is often constrained by the limited class of Strong Stability Preserving (SSP) Runge-Kutta (RK) methods. This work, ‘On the Strong Stability Preserving Property of Runge-Kutta Methods for Hyperbolic Problems’, introduces a novel analytical strategy to assess the nonlinear stability of RK schemes, even those outside the SSP class. We mathematically demonstrate that certain non-SSP RK methods can preserve critical properties like entropy stability, positivity, and Total Variation Diminishing (TVD) characteristics when coupled with appropriate spatial discretizations. Does this broadened understanding of stability open the door to more efficient and versatile numerical tools for solving challenging hyperbolic problems?
Unveiling Discontinuities: The Challenge of Hyperbolic Conservation Laws
A vast array of physical systems, from gas dynamics and fluid flow to traffic patterns and even the propagation of waves, are fundamentally described by Hyperbolic Conservation Laws. However, solutions to these equations aren’t always smooth and predictable; they frequently develop discontinuities – abrupt changes in values representing shock waves or other sharp interfaces. These discontinuities present a formidable challenge for numerical approximation techniques. Standard methods, designed for smooth functions, struggle to accurately resolve these sharp transitions, often resulting in spurious oscillations or outright instability in simulations. Consequently, obtaining reliable and physically meaningful results requires specialized approaches capable of handling these inherent discontinuities within the mathematical models.
Numerical simulations of hyperbolic partial differential equations, prevalent in modeling phenomena like fluid dynamics and gas flow, frequently encounter difficulties when solutions develop discontinuities – sharp changes in value representing shock waves or interfaces. Conventional numerical methods, designed for smoother functions, often struggle to accurately resolve these abrupt transitions. Attempts to capture these discontinuities can lead to spurious oscillations – artificial high-frequency fluctuations around the true solution – or outright instability, where the simulation diverges and produces nonsensical results. This poses a significant challenge for obtaining reliable and physically meaningful predictions, demanding the development of specialized techniques capable of handling these inherent discontinuities without compromising the overall accuracy and stability of the simulation. These specialized techniques are crucial for fields relying on accurate modeling of these complex systems.

Controlling Variation: The Power of TVD Schemes
Total Variation (TV) quantifies the total amount of variation in a function by summing the absolute differences between consecutive values; mathematically, for a discrete function u_i , TV is calculated as TV(u) = \sum_{i=1}^{n-1} |u_{i+1} - u_i| . In the context of numerical solutions to partial differential equations, a decreasing or preserved TV indicates limited spurious oscillations and suggests a stable approximation. Higher TV values correlate with increased oscillation and potential instability, as small errors can be amplified. Therefore, TV serves as a reliable metric for evaluating the robustness and accuracy of numerical schemes by directly assessing the degree of variation introduced or maintained during computation.
Total Variation Diminishing (TVD) schemes are numerical methods specifically constructed to limit the growth of oscillations in solutions to hyperbolic partial differential equations. These schemes achieve stability by ensuring that the total variation – defined as the sum of the absolute values of changes in the solution – either decreases or remains constant during the numerical evolution. By bounding the total variation, TVD schemes effectively suppress spurious oscillations that can arise from high-order approximations or discontinuities in the solution, leading to a more accurate and physically realistic approximation, particularly when solving problems involving shocks or steep gradients. This property is crucial for maintaining solution stability without requiring excessive numerical diffusion.
Lax-Friedrichs and MUSCL (Monotonic Upstream-centered Schemes for Conservation Laws) are numerical methods specifically designed to solve hyperbolic conservation laws while maintaining solution stability. Both approaches achieve this by controlling total variation (TV) during the discretization process. Lax-Friedrichs utilizes a centered difference approximation coupled with a large artificial diffusion term, effectively smoothing the solution and preventing oscillations, though at the cost of accuracy. MUSCL schemes improve upon this by employing a flux limiter – a non-linear function that restricts the slope of the reconstructed polynomial – to ensure monotonicity and prevent the introduction of spurious oscillations while preserving a higher order of accuracy than first-order schemes. By limiting the variation introduced at each step, these methods guarantee that the total variation of the approximate solution either decreases or remains constant, contributing to a stable and physically realistic result.
Beyond Continuity: High-Order Accuracy with Discontinuous Galerkin
Discontinuous Galerkin (DG) methods achieve high-order accuracy in solving hyperbolic partial differential equations (PDEs) by approximating the solution locally using polynomial basis functions within elements, without requiring continuity across element boundaries. This discontinuity allows for the natural representation of solutions containing shocks or other discontinuities, avoiding the oscillations often encountered with traditional high-order methods. The local nature of the approximation also facilitates efficient implementation and parallelization. By utilizing appropriate numerical fluxes at element interfaces, DG methods can accurately capture the propagation of discontinuities while maintaining overall solution accuracy, with error decreasing exponentially with increasing polynomial order p. This capability distinguishes DG methods as a robust choice for problems involving complex flow physics and sharp gradients.
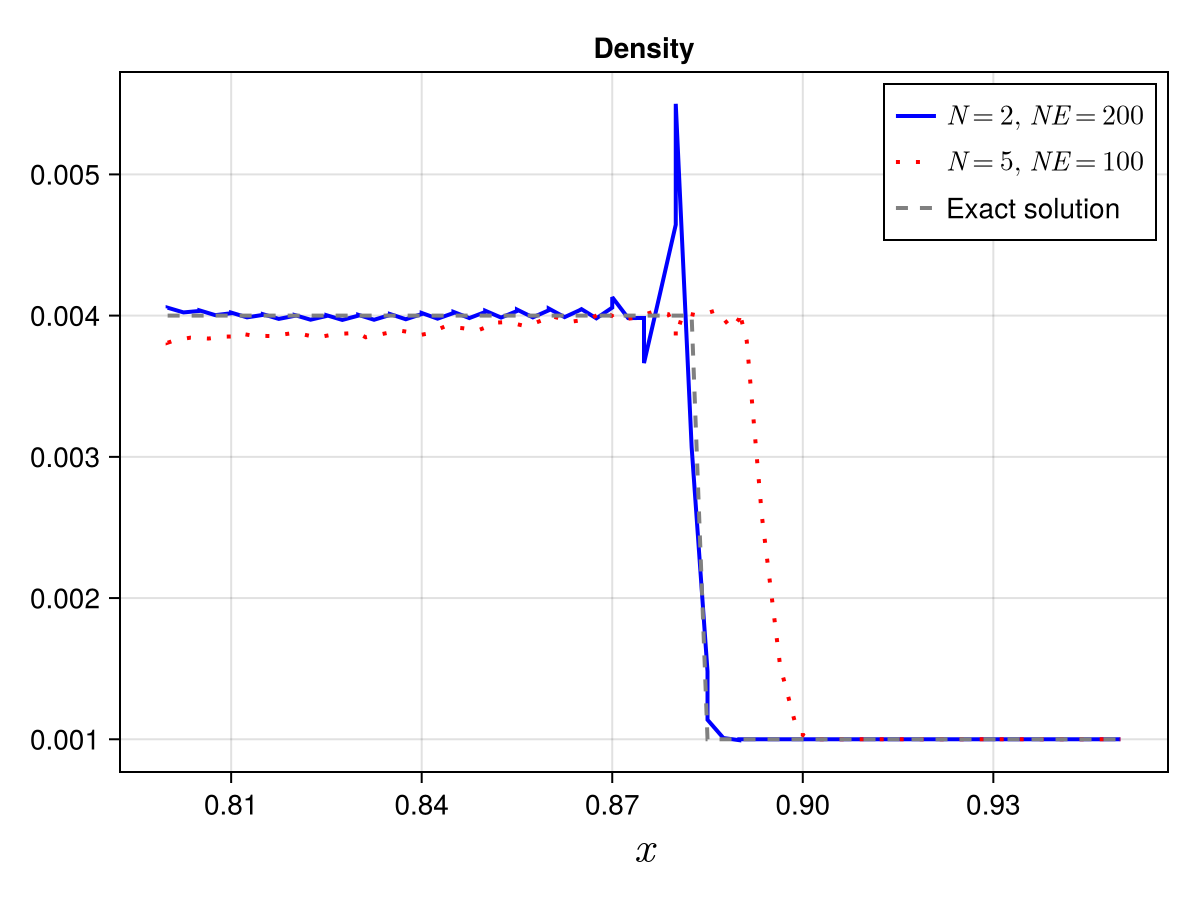
High-order Discontinuous Galerkin (DG) methods require careful selection of time integration schemes to ensure computational stability. Runge-Kutta methods are frequently employed for this purpose due to their versatility and ability to achieve a desired order of accuracy. The stability of the combined spatial-temporal discretization is dependent on both the Runge-Kutta method chosen and the specific flux reconstruction employed within the DG scheme. While Strong Stability Preserving (SSP) Runge-Kutta methods offer guaranteed stability for a given step size, research indicates that non-SSP methods, such as the fourth-order Runge-Kutta method (RK44), can also achieve stability when paired with appropriate spatial discretizations like Lax-Friedrichs, upwind, or MUSCL schemes.
Strong Stability Preserving (SSP) Runge-Kutta methods are designed to ensure numerical stability for hyperbolic partial differential equations over a defined range of time-step sizes, providing a predictable level of robustness. However, recent research indicates that traditional, non-SSP Runge-Kutta methods, such as the fourth-order Runge-Kutta method (RK44), can also achieve stability when implemented with specific spatial discretization schemes. Specifically, the use of Lax-Friedrichs, upwind, or MUSCL schemes in conjunction with non-SSP time integration allows for a stability time-step limit greater than zero, demonstrating that SSP schemes are not strictly necessary for stable high-order simulations; appropriate spatial discretization can compensate for the lack of inherent stability preservation in the time integration scheme.
Research indicates that non-Strong Stability Preserving (SSP) Runge-Kutta methods, such as RK44, can achieve a positive stability time-step limit when coupled with spatial discretization schemes like Lax-Friedrichs, upwind, or MUSCL. This finding contrasts with the conventional reliance on SSP methods to guarantee stability in high-order Discontinuous Galerkin schemes. The observed stability, even with non-SSP time integration, is dependent on the specific spatial discretization employed and suggests that the strict requirement for SSP methods may not be universally necessary, potentially allowing for a broader range of efficient time integration options.
Ensuring Physical Realism: Entropy Stability and the Method of Lines
Numerical simulations of physical systems often require approximations that can introduce errors and deviate from the true behavior dictated by conservation laws. Entropy stability offers a rigorous mathematical approach to address this challenge, ensuring that discrete solutions adhere to these fundamental physical principles. This framework relies on the concept of convex functionals – mathematical functions exhibiting a unique curvature – to define a measure of ‘entropy’ within the numerical scheme. By demonstrating that this entropy decreases or remains constant over time, researchers can prove that the numerical solution will not develop spurious oscillations or violate physical constraints like positivity. Essentially, entropy stability provides a powerful tool for verifying the reliability and accuracy of simulations, guaranteeing that the computed results remain consistent with the underlying physics, even in the presence of complex nonlinearities and long-time dynamics.
The Method of Lines presents a powerful strategy for approximating solutions to partial differential equations (PDEs). Rather than attempting to solve the PDE directly, this technique discretizes the spatial dimensions, effectively transforming the continuous problem into a system of ordinary differential equations (ODEs). This conversion is crucial because well-established and robust ODE solvers – tools rigorously tested and optimized over decades – can then be employed to march the solution forward in time. By focusing on temporal evolution within a discretized spatial framework, the Method of Lines leverages the strengths of ODE solving techniques, offering a flexible and potentially more efficient approach to tackling complex PDE problems, particularly those involving nonlinearities or intricate geometries. The accuracy of the solution is then governed by the fineness of the spatial discretization and the chosen ODE solver’s properties.
Although stable time integration schemes, such as Strong-Stability-Preserving (SSP) Runge-Kutta methods, are traditionally considered essential for long-time simulations of nonlinear hyperbolic partial differential equations (PDEs) when using the Method of Lines, recent findings suggest a broader range of viable options. The study demonstrates that certain non-SSP time integration methods, when strategically paired with carefully chosen spatial discretizations, can effectively preserve crucial mathematical properties – including convexity, positivity, and Total Variation Diminishing (TVD) stability. Surprisingly, these combinations achieve comparable stability limits to the often-favored forward Euler method, challenging the long-held belief that SSP schemes are strictly necessary for robust simulations. This opens the possibility of utilizing a wider spectrum of temporal integrators, potentially offering improved efficiency or accuracy without sacrificing stability in hyperbolic conservation law problems.
Recent research significantly reframes established practices in numerical analysis for hyperbolic conservation laws. Traditionally, simulations relied heavily on strict positivity-preserving and total variation diminishing (TVD) schemes, alongside specific time integration methods like forward Euler, to maintain stability and physical realism. However, findings demonstrate that carefully chosen spatial discretizations can, in fact, preserve crucial properties – convexity, positivity, and TVD – even when coupled with time integration schemes not conventionally considered ‘safe’ for these problems. This suggests that a broader spectrum of numerical methods can achieve comparable stability limits to those previously dictated by conservative constraints, potentially unlocking substantial computational efficiencies and offering greater flexibility in modeling complex physical phenomena. The implications are far-reaching, potentially revising current standards and encouraging exploration of alternative, high-performance schemes for solving hyperbolic partial differential equations.
The exploration of non-SSP Runge-Kutta methods achieving stability in hyperbolic conservation laws highlights a fascinating interplay between theoretical rigor and practical application. Much like discerning the underlying principles governing physical systems, this research demonstrates that established conventions – in this case, the necessity of SSP methods – are not always absolute. As Isaac Newton famously stated, “I do not know what I may seem to the world, but to myself I seem to have been only a boy playing on the seashore.” This sentiment reflects the ongoing process of discovery detailed in the article; even seemingly well-established “rules” can be revisited and refined through careful analysis and experimentation, potentially revealing unexpected stability properties beyond conventional expectations. The paper’s focus on convex functionals provides a systematic framework, akin to applying mathematical laws to natural phenomena, to understand and predict the behavior of these numerical schemes.
Beyond SSP: Charting a Course for Hyperbolic Problems
The conventional wisdom surrounding hyperbolic conservation laws has long favored Strong Stability Preserving (SSP) methods, a pragmatic approach born of necessity. This work suggests that rigidity may not be required for stability – a subtly disruptive notion. The challenge now lies in systematically characterizing which non-SSP Runge-Kutta methods exhibit this unexpectedly preserved stability, and under precisely what conditions. Each successful identification is not merely a validation, but a provocation-demanding a more generalized theoretical framework.
Future investigation should move beyond simple scalar problems. Real-world applications invariably involve multi-dimensional systems and complex geometries. Can the observed stability be extended to these more realistic scenarios, or does the added complexity necessitate a return to SSP formulations? Moreover, the role of convex functionals-intriguing as it is-remains incompletely understood. Are these functionals merely a diagnostic tool, or do they play a fundamental role in enforcing stability?
Ultimately, the goal is not simply to expand the toolbox of available numerical methods, but to deepen understanding. Every image-every numerical solution-is a challenge to understanding, not just a model input. This work casts doubt on a long-held assumption, and invites a re-examination of the underlying principles governing the stability of these notoriously difficult problems.
Original article: https://arxiv.org/pdf/2601.18947.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- How to Unlock the Mines in Cookie Run: Kingdom
- Gold Rate Forecast
- How To Upgrade Control Nexus & Unlock Growth Chamber In Arknights Endfield
- Top 8 UFC 5 Perks Every Fighter Should Use
- Solo Leveling: From Human to Shadow: The Untold Tale of Igris
- Deltarune Chapter 1 100% Walkthrough: Complete Guide to Secrets and Bosses
- Where to Find Prescription in Where Winds Meet (Raw Leaf Porridge Quest)
- Byler Confirmed? Mike and Will’s Relationship in Stranger Things Season 5
- Jujutsu: Zero Codes (December 2025)
- Quarry Rescue Quest Guide In Arknights Endfield
2026-01-29 07:06