Sensing Majorana States with Quantum Capacitance

Author: Denis Avetisyan

---

Researchers demonstrate a novel method for characterizing topological qubits by leveraging the sensitivity of quantum capacitance to the underlying fermion parity in a quantum-dot-based Kitaev chain.

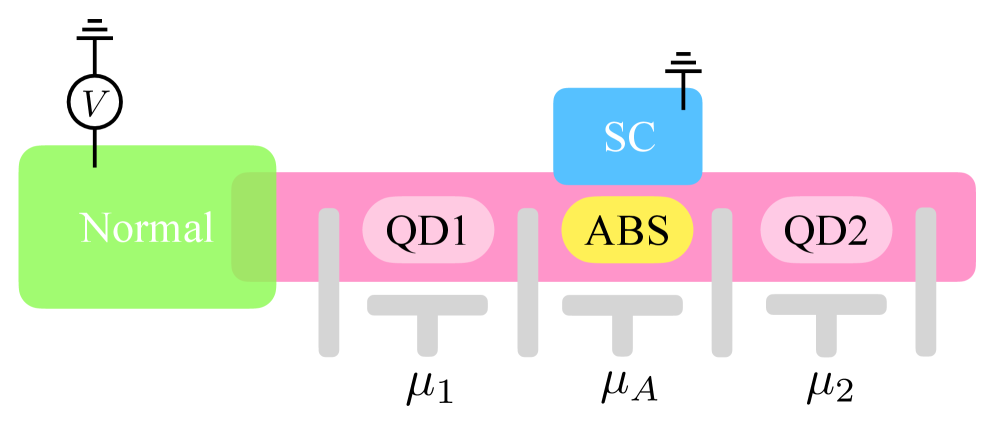
This theoretical study reveals how quantum capacitance can identify key parameters and probe parity dynamics in Kitaev chains, advancing the development of topological quantum computers.

Realizing robust topological quantum computation requires precise control and characterization of Majorana zero modes, a significant materials science challenge. This work, ‘Quantum capacitance and parity switching of a quantum-dot-based Kitaev chain’, theoretically investigates the quantum capacitance of a minimal Kitaev chain-an array of quantum dots coupled via superconductivity-to provide a novel diagnostic tool. We find that quantum capacitance measurements can identify optimal device parameters and reveal the interplay between external and intrinsic mechanisms governing fermion parity switching. Could this approach unlock a pathway towards more reliable and scalable platforms for topological quantum information processing?

---

Beyond Semiconductors: The Pursuit of Coherent Qubits

The pursuit of stable and scalable quantum computation necessitates a departure from conventional semiconductor materials, which increasingly exhibit limitations as qubit technology advances. Traditional semiconductors struggle with maintaining the delicate quantum states – coherence – required for complex calculations, succumbing to decoherence from environmental noise and material imperfections. Consequently, researchers are actively investigating alternative physical platforms, seeking materials and systems inherently more resistant to these disturbances. These novel approaches range from trapped ions and topological qubits to, significantly, solid-state systems leveraging the unique properties of materials like quantum dots and superconductors – promising avenues for building qubits that can maintain coherence for longer durations and enable more complex quantum operations, ultimately paving the way for practical quantum computers.

The pursuit of stable and scalable quantum computation has driven exploration beyond conventional semiconductor materials, leading to significant interest in quantum dot-superconductor hybrid systems. These structures ingeniously combine the charge confinement and tunability of quantum dots – nanocrystals exhibiting quantum mechanical properties – with the dissipationless current flow and macroscopic quantum phenomena of superconductors. This synergy allows for the creation of novel quantum states, specifically Andreev bound states E = \sqrt{\epsilon^2 + \Delta^2}, at the interface, where electrons and holes are bound together due to the superconducting proximity effect. By carefully engineering these hybrids, researchers aim to realize topologically protected qubits, potentially overcoming the decoherence challenges that plague many current quantum computing architectures. The ability to control and manipulate these Andreev states promises a pathway toward robust and scalable quantum information processing, capitalizing on the distinct advantages offered by both quantum dots and superconductivity.

The emergence of Andreev bound states (ABS) within quantum dot-superconductor hybrid structures represents a pivotal mechanism for manipulating quantum information. These unique states arise when an electron from the quantum dot interacts with a Cooper pair in the superconductor, resulting in a quasiparticle with energy near zero. Critically, the spatial extent of the ABS can be tuned by adjusting the properties of the quantum dot and the interface with the superconductor, effectively controlling the range of interactions between qubits defined within the dots. This tunability allows for the creation of entangled states and the implementation of controlled-NOT gates, essential building blocks for scalable quantum computation. Furthermore, the inherent robustness of the ABS against certain types of decoherence offers a pathway toward creating more stable and reliable qubits, ultimately advancing the field of quantum information processing. E = \sqrt{\epsilon^2 + \Delta^2}

Engineering Topology: The Kitaev Chain and Majorana Modes

The Kitaev chain is a one-dimensional system engineered from a periodic arrangement of quantum dots connected by superconducting leads. This specific architecture is predicated on realizing Majorana zero modes (MZMs) at the ends of the chain. These MZMs emerge as a consequence of combining proximity-induced superconductivity with strong spin-orbit coupling and an applied magnetic field. The chain’s design leverages the unique properties of p-wave superconductivity, which, although not directly present, is effectively emulated through the interplay of these components. Crucially, the MZMs are not conventional fermionic excitations but rather are their own antiparticles, leading to non-Abelian statistics and potential applications in topologically protected quantum computation.

Topological protection in Majorana zero modes arises from their non-local nature and the system’s symmetry, which prevents them from being easily disrupted by local perturbations. Unlike conventional quantum bits which are susceptible to decoherence from environmental noise, the information encoded in Majorana modes is distributed across the entire system, requiring a global disturbance to alter the quantum state. This inherent robustness is crucial for building stable and fault-tolerant quantum computers, as it minimizes the impact of errors and allows for more complex and prolonged quantum computations. The \mathbb{Z}_2 topological protection guarantees that these modes are immune to local perturbations that do not close the superconducting gap, making them promising candidates for scalable quantum information processing.

Realization of Majorana zero modes within the Kitaev chain necessitates precise control over system parameters. Specifically, successful implementation of the model requires maintaining Zeeman splitting values of E_{Z1} = E_{Z2} = 3 and onsite Coulomb energies of U_1 = U_2 = 5. These values define the energy landscape and hybridization characteristics of the quantum dots and superconducting regions, directly influencing the formation and localization of the Majorana modes at the chain’s ends. Deviation from these parameters can disrupt the topological protection and prevent the emergence of the desired zero-energy states, hindering potential applications in quantum computation.

Revealing the Invisible: Quantum Capacitance as a Probe

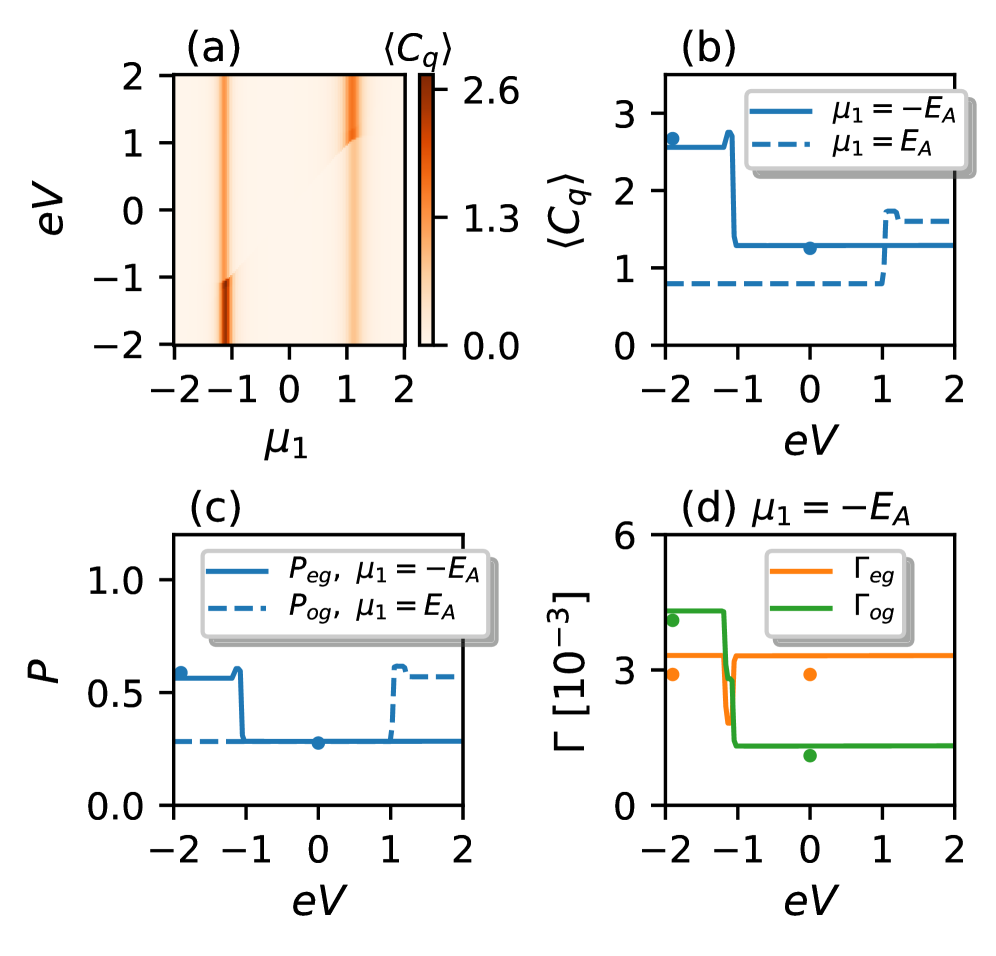
Quantum capacitance, arising from the density of states at the Fermi level, offers a sensitive method for determining the parity of fermion states in nanoscale devices. Unlike conventional capacitance which is limited by the device size, quantum capacitance is directly related to the changes in electron density induced by variations in gate voltage, even with few electrons. This allows for the differentiation between even and odd occupation numbers of quantum states, providing a means to detect the presence or absence of a single electron or, crucially, a Majorana zero mode. Measurements are performed by analyzing the differential capacitance dC/dV as a function of applied voltage, with signatures indicative of parity changes appearing as distinct features in the capacitance spectrum.

Quantum capacitance measurements directly probe the density of states in a nanoscale system, offering a means to detect the presence of Majorana zero modes within the Kitaev chain. Unlike traditional conductance measurements which can be influenced by background states, quantum capacitance is sensitive to changes in the electronic density of states at the Fermi level, specifically revealing the unique characteristics of these modes. The technique relies on measuring the differential capacitance C = \frac{dQ}{dV} as a function of gate voltage, where a distinct signature emerges due to the localized nature and zero-energy characteristic of Majorana zero modes. This direct detection method provides a complementary approach to verifying their existence, offering advantages in differentiating Majorana modes from trivial Andreev bound states.

The existence of Majorana zero modes is strongly indicated by the observation of zero-bias conductance peaks in tunneling experiments. These peaks arise when the tunneling rate between the quantum dot and the Kitaev chain reaches values of t_{sc} = 0.1 and t_{sf} = 0.03. These specific tunneling rates facilitate the detection of the unique electronic properties associated with Majorana modes, providing a measurable signature distinct from conventional fermionic states and serving as key evidence for their presence in the system.

The Pursuit of Stability: Tuning the Majorana Sweet Spot

The pursuit of topologically protected qubits hinges on identifying and meticulously controlling the ‘Majorana sweet spot’ – a specific configuration of parameters where Majorana zero modes exhibit maximal robustness. These exotic quasiparticles, predicted to exist at the edges of certain superconducting materials, are inherently shielded from local environmental noise due to their non-local nature. Within this ‘sweet spot’, the energy separation between the Majorana zero modes and excited states is maximized, effectively minimizing the impact of decoherence mechanisms. This parameter regime isn’t a single point, but rather a region defined by factors like magnetic field, chemical potential, and proximity coupling to other materials; careful calibration of these elements is crucial for maintaining the quantum information encoded in these states. Successfully locating and stabilizing this ‘sweet spot’ represents a significant step towards realizing fault-tolerant quantum computation, as it directly addresses the challenge of preserving delicate quantum coherence.

The precise characteristics of the ‘Majorana sweet spot’ – the optimal conditions for stable Majorana zero modes – are heavily influenced by specific electron transport mechanisms. Elastic cotunneling, a process where electrons tunnel through a quantum dot without directly exciting it, and crossed Andreev reflection, where an electron enters a superconductor and a hole exits, both contribute significantly to the local density of states near the Majorana modes. These processes effectively ‘smear’ the ideal conditions for a perfectly sharp zero mode, broadening the sweet spot and impacting its robustness against perturbations. Understanding how these mechanisms interact – and are affected by factors like temperature and applied voltage – is therefore crucial for designing and controlling Majorana-based qubits, as they directly dictate the achievable coherence times and the fidelity of quantum operations. The interplay between these tunneling events establishes the energy scales over which the Majorana modes remain protected, and ultimately defines the boundaries of the stable parameter regime.

Maintaining the delicate quantum coherence necessary for topological qubits relies heavily on precise external control and a thorough understanding of quasiparticle poisoning. These Majorana-based qubits are particularly susceptible to decoherence induced by unwanted quasiparticles-excitations that can disrupt the zero-mode states. Research indicates the energy scale associated with quasiparticle poisoning, represented as k_B T_{qpp}, is often on par with the superconducting gap, \Delta_0. This comparability means even small numbers of quasiparticles can significantly degrade qubit performance. Consequently, strategies involving normal reservoirs – carefully tuned metallic contacts – are employed to manipulate and mitigate the presence of these disruptive excitations. By actively controlling the environment and minimizing quasiparticle contamination, scientists aim to extend coherence times and unlock the potential of robust, topologically protected quantum computation.

The pursuit of stable Majorana zero modes, as detailed in this theoretical investigation of quantum capacitance within Kitaev chains, reveals a familiar pattern. The sensitivity to parameters – the ‘sweet spot’ where these modes flourish – is not merely a technical hurdle, but a reflection of underlying human tendencies. As Aristotle observed, “The ultimate value of life depends upon awareness and the power of contemplation rather than upon mere survival.” This resonates deeply; the quest for topological quantum computing isn’t simply about building a more powerful computer, but about meticulously controlling a system so fragile it mirrors the precariousness of hope itself. The article’s focus on parity switching-detecting changes in fermion parity-highlights the inherent instability and the need for precise control, mirroring the fleeting nature of any perceived stability in complex systems.

Where Do We Go From Here?

The exploration of quantum capacitance as a diagnostic tool for Kitaev chains feels less like a triumph of engineering and more like a clever exploitation of inherent fragility. The ‘sweet spot’ isn’t a point of stability, but a zone of exquisite sensitivity – a place where the slightest perturbation reveals the underlying quantum state. This isn’t about building robust machines; it’s about learning to read the whispers of quantum mechanics before they dissolve into noise. The predictable failures will, of course, prove far more instructive than any immediate success.

The paper’s focus on parity switching is particularly telling. The attempt to control fermion parity suggests a fundamental misunderstanding of the system. It isn’t about imposing order, but about accurately measuring the inevitable fluctuations. Every deviation from expected parity isn’t an error; it’s a window into the complex interplay of Andreev bound states and the subtle forces shaping the Majorana zero modes. The limitations in current measurement techniques, frankly, aren’t technical hurdles – they are a reflection of the sheer difficulty in observing something fundamentally ephemeral.

Future work will undoubtedly focus on mitigating decoherence. However, a more fruitful path might lie in embracing it. Instead of striving for perfect isolation, perhaps one can devise architectures that utilize the inherent randomness. After all, the human brain doesn’t function by eliminating noise, but by filtering and interpreting it. The same principle may well apply to building a quantum computer-not as a temple of perfect logic, but as a controlled chaos machine.

---

Original article: https://arxiv.org/pdf/2601.20252.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

See also:

• How to Unlock the Mines in Cookie Run: Kingdom

• Gold Rate Forecast

• How To Upgrade Control Nexus & Unlock Growth Chamber In Arknights Endfield

• Top 8 UFC 5 Perks Every Fighter Should Use

• Jujutsu: Zero Codes (December 2025)

• Solo Leveling: From Human to Shadow: The Untold Tale of Igris

• Quarry Rescue Quest Guide In Arknights Endfield

• Byler Confirmed? Mike and Will’s Relationship in Stranger Things Season 5

• Where to Find Prescription in Where Winds Meet (Raw Leaf Porridge Quest)

• Deltarune Chapter 1 100% Walkthrough: Complete Guide to Secrets and Bosses

2026-01-29 13:49