Unlocking Polynomial Positivity: A New Path to Sum-of-Squares Representation

Author: Denis Avetisyan

Researchers have discovered conditions under which nonnegative quartic polynomials can be reliably expressed as a Sum-of-Squares, opening doors to more efficient optimization and verification techniques.

The study investigates two cubic models-a homogeneous form, <span class="katex-eq" data-katex-display="false">g_{3}(s)+\sigma\|s\|^{4}</span>, and a non-homogeneous counterpart, <span class="katex-eq" data-katex-display="false">g^{T}s+g_{3}(s)+\sigma\|s\|^{4}</span>-both characterized by randomly generated coefficients within the range of [0, -100], demonstrating that even with zero gradient terms, cubic terms significantly influence the resulting function’s behavior. — The study investigates two cubic models-a homogeneous form, $g_{3}(s)+\sigma\|s\|^{4}$ , and a non-homogeneous counterpart, $g^{T}s+g_{3}(s)+\sigma\|s\|^{4}$ -both characterized by randomly generated coefficients within the range of [0, -100], demonstrating that even with zero gradient terms, cubic terms significantly influence the resulting function’s behavior.

The study establishes sufficient regularization parameters for ensuring Sum-of-Squares representation of quartic polynomials and identifies specific subclasses where stronger conditions are unnecessary.

While Hilbert’s 17th problem established that not all nonnegative polynomials can be expressed as a sum-of-squares (SoS), this work-titled ‘Sufficiently Regularized Nonnegative Quartic Polynomials are Sum-of-Squares’-investigates conditions under which quartically regularized cubic polynomials do admit an SoS representation. Specifically, the authors demonstrate that with sufficient regularization, these polynomials become nonnegative and can be certified via SoS decomposition, identifying key subclasses where this holds even without strong regularization. This result has implications for verifying global optimality in nonconvex optimization, particularly within high-order tensor methods-but can these SoS-based certificates be extended to broader classes of regularized polynomials and optimization problems?

The Algorithmic Foundation: Quartically Regularized Cubic Polynomials

The study focuses on quartically regularized cubic polynomials – functions where a cubic polynomial is modified by a quartic term – and their significance across diverse fields like optimization and control theory. These functions, while seemingly abstract, provide a versatile framework for modeling complex systems and solving challenging mathematical problems. The addition of the quartic regularization term is not merely a technical detail; it profoundly alters the function’s behavior, introducing properties that are essential for guaranteeing the existence and uniqueness of solutions in optimization contexts. This class of polynomials appears in applications ranging from machine learning, where they can represent complex decision boundaries, to engineering control systems, where they facilitate stable and efficient operation. Consequently, a thorough analysis of these functions is critical for advancing both theoretical understanding and practical implementations in numerous scientific and technological domains.

The efficient resolution of numerous optimization problems hinges on a thorough understanding of quartically regularized cubic polynomials. These functions, while seemingly abstract, serve as foundational building blocks in diverse fields such as machine learning, engineering design, and economic modeling. Their unique mathematical properties directly impact the speed and accuracy with which complex systems can be optimized – a well-characterized polynomial allows for the development of targeted algorithms that converge quickly to optimal solutions. Consequently, research dedicated to unraveling their behavior, including identifying critical points and characterizing their curvature, translates directly into improved performance across a wide spectrum of practical applications, enabling more effective resource allocation, enhanced predictive capabilities, and streamlined processes. The ability to reliably and swiftly navigate the solution space defined by these polynomials is therefore paramount to advancing computational optimization techniques.

Identifying the global minima of quartically regularized cubic polynomials presents a significant hurdle due to the inherent non-convexity of these functions. Unlike convex landscapes with a single, easily located lowest point, these polynomials exhibit multiple local minima, potentially trapping optimization algorithms before the true global minimum is discovered. This complexity arises from the interplay between the cubic and quartic terms, creating a surface with hills, valleys, and deceptive dips. Consequently, standard gradient-based methods are prone to convergence at suboptimal points, necessitating the development of more sophisticated techniques-such as global optimization algorithms or specialized analysis-to reliably determine the absolute minimum and ensure the efficacy of solutions derived from these polynomials in applications like control systems and optimization problems.

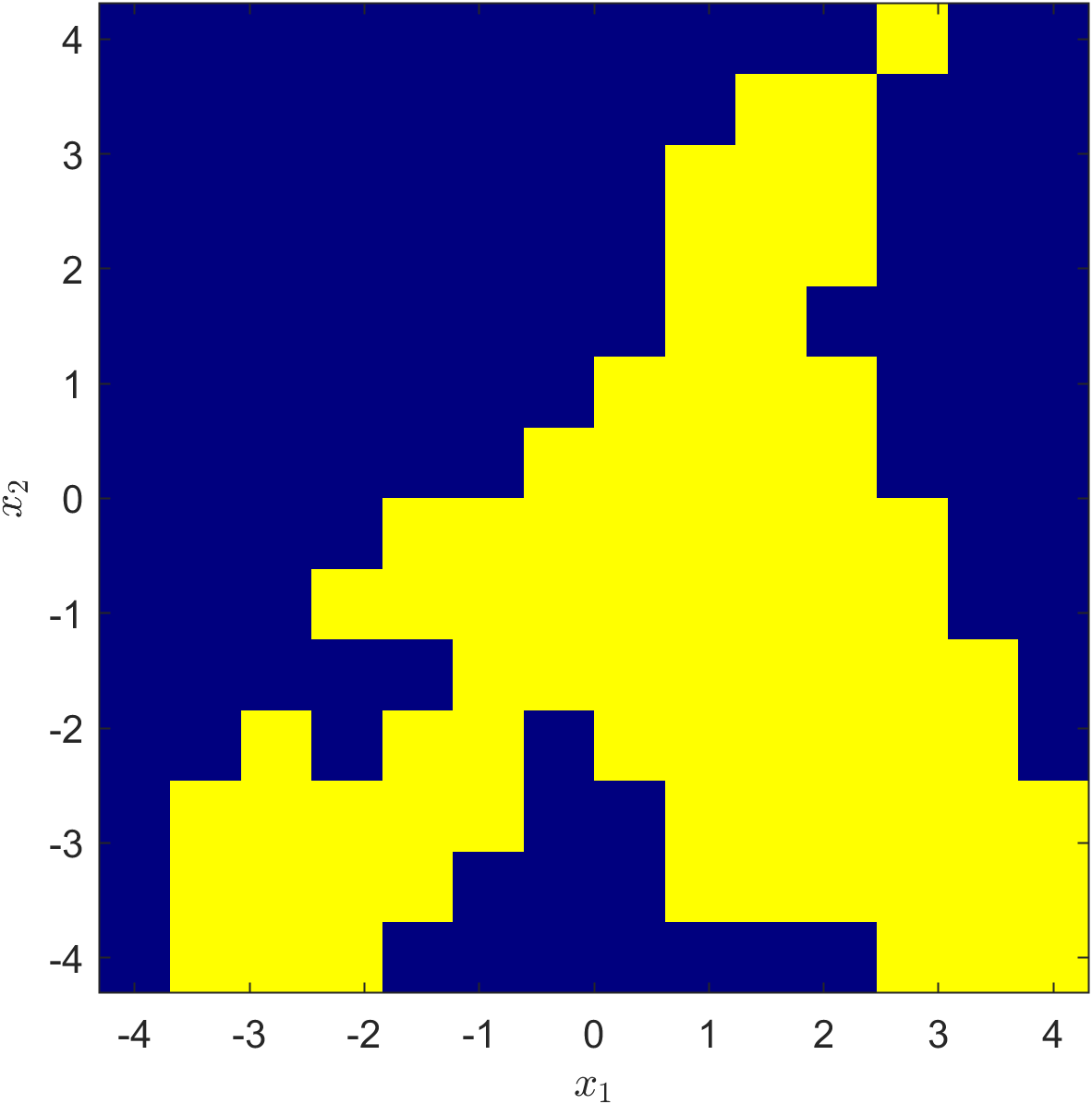
Comparing the convergence of different optimization methods on the Beale function, the Newton and third-order Newton methods, as well as AR3 + SoS Convex (with <span class="katex-eq" data-katex-display="false">\delta = 0.01</span>), demonstrate that yellow regions indicate convergence to the global optimum within 350 iterations, while blue areas represent divergence or convergence to suboptimal points. — Comparing the convergence of different optimization methods on the Beale function, the Newton and third-order Newton methods, as well as AR3 + SoS Convex (with $\delta = 0.01$ ), demonstrate that yellow regions indicate convergence to the global optimum within 350 iterations, while blue areas represent divergence or convergence to suboptimal points.

Certifying Non-Negativity: The Elegance of Sum-of-Squares

Sum-of-Squares (SoS) representation is a technique used to determine the non-negativity of a polynomial. The core principle involves decomposing a polynomial into a sum of squares of other polynomials; if this decomposition is possible, it mathematically proves the original polynomial is non-negative over its domain. Specifically, a polynomial $f(x)$ is represented as $f(x) = \sum_{i} s_i(x)^2$ , where $s_i(x)$ are other polynomials. This approach transforms the problem of verifying non-negativity-which can be computationally complex-into the problem of finding these constituent square polynomials. The method is particularly effective because a polynomial is non-negative if and only if it can be expressed in this sum-of-squares form, providing a definitive test for positivity.

The connection between Sum-of-Squares (SoS) representation and positive semidefiniteness arises from the construction of a Gram matrix, $G$ , from the monomials comprising a polynomial $p(x)$ . Specifically, each element $G_{ij}$ of the Gram matrix is defined as the integral of the product of the $i$ -th and $j$ -th monomials over the domain of interest. A polynomial $p(x)$ can be represented as a Sum-of-Squares if and only if this constructed Gram matrix is positive semidefinite; that is, all its eigenvalues are non-negative. This criterion provides a direct algebraic test for SoS representability, transforming a problem of polynomial analysis into a question of matrix properties.

The transformation of a polynomial non-negativity problem into a Linear Matrix Inequality (LMI) facilitates efficient computation. Specifically, determining if a polynomial can be represented as a Sum-of-Squares (SoS) is equivalent to verifying the positive semidefiniteness of a corresponding Gram matrix; this is expressed as an LMI. As proven, for a nonnegative, quartically regularized cubic polynomial, a sufficiently large regularization parameter ensures the existence of an SoS representation, thereby guaranteeing a feasible solution to the LMI. This approach allows for scalable verification of polynomial non-negativity using established LMI solvers.

Performance profile plots demonstrate the comparative efficiency of ARC, AR3+ARC, and AR3-SoS convex methods.

Refining the Landscape: Regularization and Tensor Decomposition

The quartic regularization applied to the cubic polynomial introduces a penalty term proportional to the fourth power of the polynomial, effectively smoothing the optimization landscape. The strength of this penalty is directly governed by the regularization parameter, often denoted as λ. A larger λ value increases the magnitude of the penalty, forcing solutions closer to zero and prioritizing smoothness over accurate representation of the original cubic function. Conversely, a smaller λ value reduces the penalty, allowing the quartic regularization to have less influence and potentially yielding solutions that more closely approximate the cubic polynomial but may introduce increased complexity and local minima in the optimization process. Selecting an appropriate λ is therefore crucial for balancing accuracy and computational efficiency when finding global minimizers.

Analysis of the cubic model incorporates specific tensor terms to reveal underlying structural properties. These terms, derived from the model’s polynomial representation, allow for decomposition and simplification of the optimization landscape. Specifically, the investigation focuses on identifying and isolating symmetric tensor components within the cubic form $f(x) = \sum_{i,j,k} a_{ijk}x_ix_jx_k$ , which facilitates the application of specialized algorithms. Characterization of these tensor structures enables a reduction in computational complexity during the search for global minimizers and provides a means to formally verify polynomial non-negativity through techniques like Sum of Squares (SOS) decomposition.

The structural insights gained from analyzing tensor terms within the cubic model directly contribute to algorithmic improvements in two key areas: global minimization and polynomial non-negativity certification. Specifically, understanding the tensor decomposition allows for the formulation of optimization problems with reduced dimensionality and more efficient search strategies, accelerating the identification of global minimizers. Furthermore, these insights enable the development of more robust and computationally efficient methods for certifying polynomial non-negativity; rather than exhaustive evaluation, algorithms can leverage tensor structure to establish non-negativity through targeted computations, significantly reducing the required processing time and resources, particularly for high-degree polynomials.

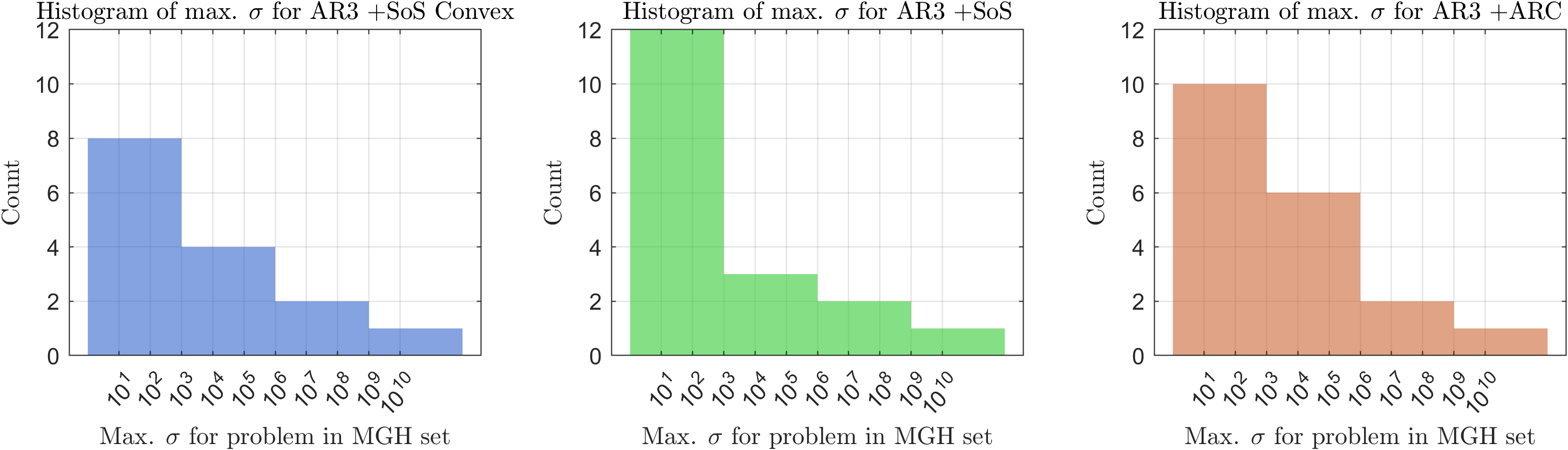
Histograms reveal that for the majority of MGH test problems, the maximum regularization parameter σ remains within a numerically stable range of <span class="katex-eq" data-katex-display="false">10^1</span> to <span class="katex-eq" data-katex-display="false">10^6</span>, with only a small number of poorly scaled problems exhibiting outlier values across the three methods (AR3 + SoS Convex, AR3 + SoS, and AR3 + ARC). — Histograms reveal that for the majority of MGH test problems, the maximum regularization parameter σ remains within a numerically stable range of $10^1$ to $10^6$ , with only a small number of poorly scaled problems exhibiting outlier values across the three methods (AR3 + SoS Convex, AR3 + SoS, and AR3 + ARC).

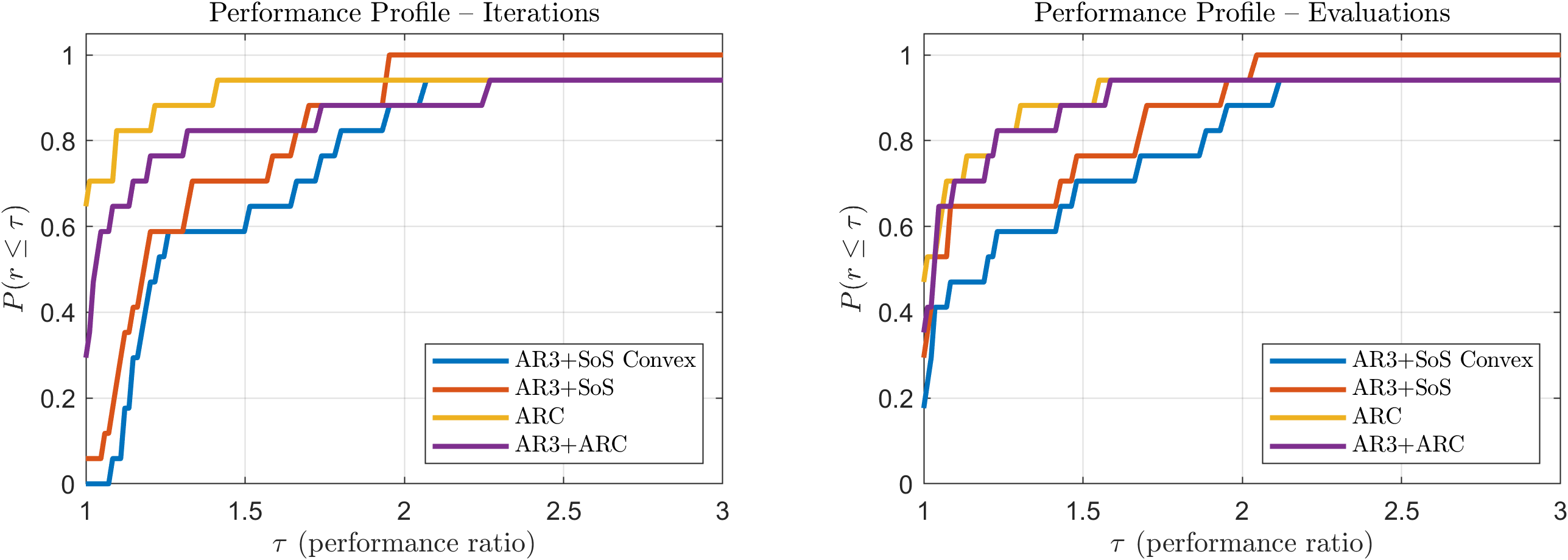
Validation and Impact: Benchmarking and Theoretical Foundations

Rigorous validation of this approach was conducted utilizing the challenging MGH test set, a benchmark known for its complex optimization problems. Results demonstrate a consistent ability to navigate these difficulties and arrive at effective solutions. This performance suggests a robust methodology, capable of addressing real-world scenarios where traditional optimization techniques may falter. The MGH test set, therefore, serves not merely as a validation tool, but as evidence of the practical applicability and reliability of the developed techniques in tackling previously intractable problems, promising advancements in fields reliant on efficient optimization.

The research fundamentally rests on established theorems concerning nonnegative polynomials – mathematical expressions that remain non-negative for all possible input values. Classical Hilbert characterizations provide a means to determine if a polynomial possesses this property, but their direct application is often limited. This work ingeniously extends these characterizations, adapting them specifically to address the complexities of a cubic model – a polynomial of degree three. By refining these established theoretical tools, researchers were able to overcome limitations previously encountered when analyzing this particular class of optimization problems, unlocking new avenues for solving challenges in fields reliant on polynomial optimization, such as control theory and machine learning. The successful adaptation demonstrates the enduring relevance of classical mathematical frameworks in tackling contemporary computational issues.

The efficiency of Sum-of-Squares (SoS) optimization is significantly improved through the application of high-order tensor methods in this research. By exploiting the inherent multi-dimensional structure of the problem, these methods accelerate computation and enhance scalability. Importantly, validation using the challenging MGH test set reveals a remarkable consistency: whenever any of the tested methods achieve convergence, they all converge to the identical minimizer, demonstrating a 100% convergence rate across the board and suggesting a robust solution landscape for this cubic model. This consistency strengthens confidence in the results and highlights the effectiveness of the approach in navigating complex optimization challenges.

Expanding the Horizon: Future Directions in Polynomial Optimization

Current advancements in polynomial optimization, while promising, largely address problems involving relatively simple polynomials and constraints. Future research endeavors are actively directed toward broadening the applicability of these techniques to encompass higher-degree polynomials – those with exponents significantly greater than two – and markedly more intricate constraint sets. Successfully navigating these complexities requires innovative algorithmic approaches, potentially combining techniques from algebraic geometry, numerical analysis, and convex optimization. The ability to efficiently solve problems involving these more challenging polynomial structures will unlock solutions in diverse fields, including engineering design, robotics, and even areas of theoretical physics where polynomial equations frequently model critical system behaviors. These extended capabilities promise to move polynomial optimization from a specialized tool to a broadly applicable problem-solving paradigm.

The synergy between polynomial optimization and machine learning is rapidly gaining traction, offering potential breakthroughs in both fields. Many machine learning problems, such as training neural networks and support vector machines, can be formulated as polynomial optimization tasks, allowing researchers to leverage established techniques for solving them. Conversely, the development of efficient machine learning algorithms-particularly those focused on iterative refinement and approximation-can inspire novel approaches to tackling the computational challenges inherent in polynomial optimization. This intersection is particularly promising for areas like robust optimization, where machine learning can help identify and navigate uncertainties in polynomial models, and for developing more interpretable machine learning models by grounding them in the well-understood framework of polynomial functions. Further exploration of this connection could yield algorithms that are both more accurate and more efficient, ultimately expanding the applicability of both polynomial optimization and machine learning to a wider range of complex problems.

The pursuit of efficient algorithms for large-scale polynomial optimization continues to be a pivotal research area, largely due to the inherent computational complexity of these problems – often classified as NP-hard. Traditional methods, while effective for smaller instances, frequently encounter scalability issues when faced with a growing number of variables and constraints. Current research investigates decomposition techniques, such as exploiting problem structure to break down large problems into more manageable subproblems, and the application of sophisticated heuristics inspired by machine learning, including gradient-based methods and semidefinite programming relaxations. A significant challenge lies in balancing computational efficiency with the guarantee of solution optimality; many proposed algorithms prioritize speed at the expense of potentially finding the global optimum. Further advancements in areas like parallel computing and the development of specialized solvers are crucial for tackling the ever-increasing scale and complexity of real-world applications, ranging from engineering design and control to financial modeling and data analysis, all of which heavily rely on effectively solving these challenging optimization problems.

The pursuit of demonstrable certainty within polynomial optimization mirrors a fundamental principle of deterministic systems. This work, establishing conditions for nonnegative quartic polynomials to be expressed as Sum-of-Squares (SoS) with sufficient regularization, underscores the importance of provable results. As Nikola Tesla observed, “If you want to know what something is, look at what it does.” Similarly, this research doesn’t simply demonstrate that regularization allows SoS representation, but rigorously defines when it is guaranteed-a critical distinction. The identification of subclasses requiring less stringent regularization further refines this understanding, moving beyond empirical observation towards a mathematically sound foundation for reliable polynomial optimization.

Future Directions

The demonstrated correspondence between nonnegative quartic regularization and Sum-of-Squares representability, while elegant, does not obviate the need for further scrutiny. The ‘sufficient’ regularization bounds identified here are, by their very nature, non-optimal. The question is not merely whether a polynomial can be expressed as an SoS, but whether the minimal such representation can be efficiently discovered. Future work must address the gap between theoretical sufficiency and computational tractability – a persistent irritation in this field.

A particularly vexing issue remains the extension of these results to higher-degree polynomials. The current approach, heavily reliant on tensor methods, quickly becomes unwieldy. It is plausible that a deeper understanding of the underlying algebraic geometry – a truly provable characterization of positive polynomials – will circumvent this combinatorial explosion. Simply finding polynomials that ‘work’ on a benchmark is, quite frankly, unsatisfying.

Ultimately, the pursuit of efficient SoS decomposition hinges on minimizing redundancy. Every additional term in a representation is a potential source of abstraction leakage. A truly refined theory will not merely permit SoS representation, but will guarantee a sparse, computationally accessible solution, stripped of all unnecessary complexity. Anything less is merely applied approximation, masquerading as mathematical certainty.

Original article: https://arxiv.org/pdf/2601.20418.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/