Taming the Bits: A New Approach to Efficient AI Inference

Author: Denis Avetisyan

Researchers have developed a novel quantization framework that reshapes the underlying mathematical landscape of AI models to enable significantly more efficient low-bit inference.

HeRo-Q achieves stable quantization by reshaping the Hessian spectrum through a lightweight linear transformation that diminishes large, outlying eigenvalues and caps the maximum eigenvalue, ultimately reducing the loss landscape’s susceptibility to quantization noise and enabling efficient low-bit inference.

HeRo-Q stabilizes post-training quantization by compressing the Hessian spectrum and redistributing quantization noise for robust low-bit performance.

Post-training quantization, while effective for model compression, often exhibits a counterintuitive ‘low error, high loss’ phenomenon due to its focus on minimizing quantization error alone. This paper introduces ‘HeRo-Q: A General Framework for Stable Low Bit Quantization via Hessian Conditioning’, a novel approach that addresses this by reshaping the loss landscape through a learnable rotation-compression matrix, effectively reducing sensitivity to quantization noise via Hessian spectrum conditioning. Experiments demonstrate that HeRo-Q consistently outperforms state-of-the-art methods-including GPTQ, AWQ, and SpinQuant-even in extremely low-bit regimes like $\mathcal{N}=3$ and $\mathcal{N}=4$ , boosting accuracy and mitigating logical collapse. Could this framework unlock even more aggressive quantization levels, paving the way for truly efficient large language model deployment on resource-constrained devices?

The Inevitable Cost of Scale

Contemporary large language models, such as those in the Llama and Qwen families, have demonstrated remarkable capabilities across a spectrum of natural language tasks, frequently achieving state-of-the-art results. However, this impressive performance comes at a significant cost; these models are inherently computationally intensive. Training and even deploying them requires vast amounts of processing power, memory, and energy. The sheer scale of parameters – often billions or even trillions – necessitates specialized hardware and substantial infrastructure, limiting accessibility and hindering wider adoption. This creates a crucial need for techniques that can reduce the computational burden without drastically sacrificing the quality of the generated text, prompting research into model compression and optimization strategies.

Large language models, while achieving remarkable results, present a significant challenge regarding computational cost. Post-training quantization – the process of reducing the precision of model weights and activations – offers a potential solution, but simplistic approaches often introduce substantial quantization error, leading to a noticeable drop in accuracy. The HeRo-Q method directly tackles this issue by selectively quantizing weights based on their saliency and contribution to the overall model performance. This innovative strategy allows for more aggressive quantization – reducing precision to lower bit-widths – without incurring the typical accuracy losses, ultimately achieving performance remarkably close to that of full-precision (FP16) models while drastically reducing computational demands and memory footprint. The result is a pathway to deploy powerful language models on resource-constrained hardware without sacrificing quality.

HeRo-Q enhances quantization robustness by applying a learned linear transformation <span class="katex-eq" data-katex-display="false">\mathbf{T}=\mathbf{D}_{\alpha}^{-1}\mathbf{R}</span>-constructed from a diagonal scaling matrix <span class="katex-eq" data-katex-display="false">\mathbf{D}_{\alpha}</span> and an orthogonal rotation matrix <span class="katex-eq" data-katex-display="false">\mathbf{R}</span> learned via the Cayley transform-to reshape the weight space and mitigate sensitivity to quantization noise arising from high Hessian curvature. — HeRo-Q enhances quantization robustness by applying a learned linear transformation $\mathbf{T}=\mathbf{D}_{\alpha}^{-1}\mathbf{R}$ -constructed from a diagonal scaling matrix $\mathbf{D}_{\alpha}$ and an orthogonal rotation matrix $\mathbf{R}$ learned via the Cayley transform-to reshape the weight space and mitigate sensitivity to quantization noise arising from high Hessian curvature.

The Loss Landscape: Why Sensitivity Matters

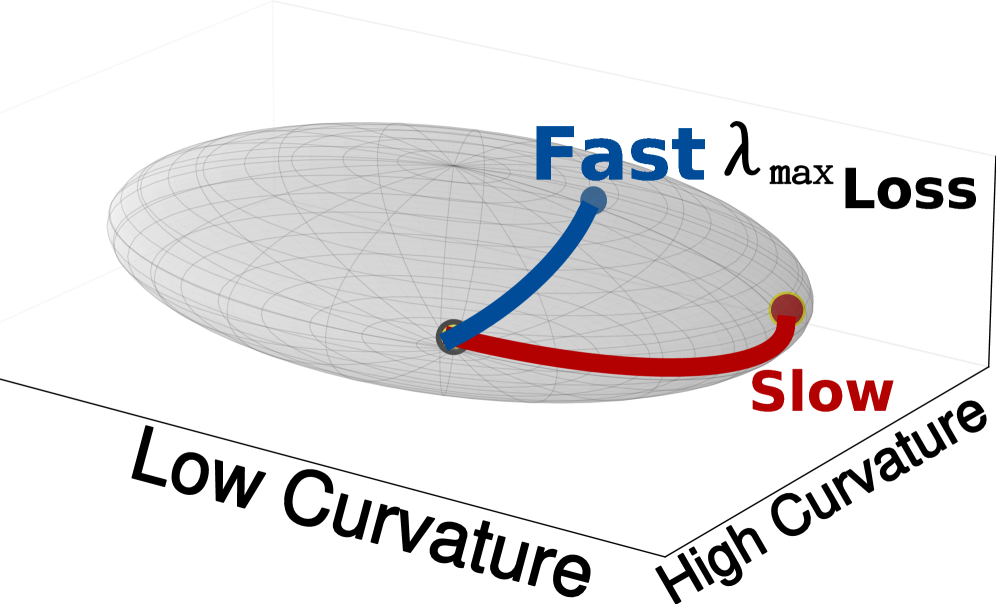
The Hessian matrix, a square matrix of second-order partial derivatives of a loss function, describes the local curvature of the loss landscape with respect to the model’s parameters. Each element $H_{ij}$ represents the rate of change of the gradient of the loss function with respect to parameter $\theta_i$ when parameter $\theta_j$ is varied. Positive definite Hessians indicate a local minimum with curvature in all directions, while indefinite Hessians suggest a saddle point. The eigenvalues of the Hessian determine the principal curvatures; large positive eigenvalues indicate steep ascent directions, large negative eigenvalues indicate steep descent directions, and small eigenvalues suggest flat regions. Consequently, analyzing the Hessian allows for identification of parameters where small perturbations will cause significant changes in the loss, indicating high sensitivity, and conversely, directions where perturbations have minimal impact, indicating low sensitivity.

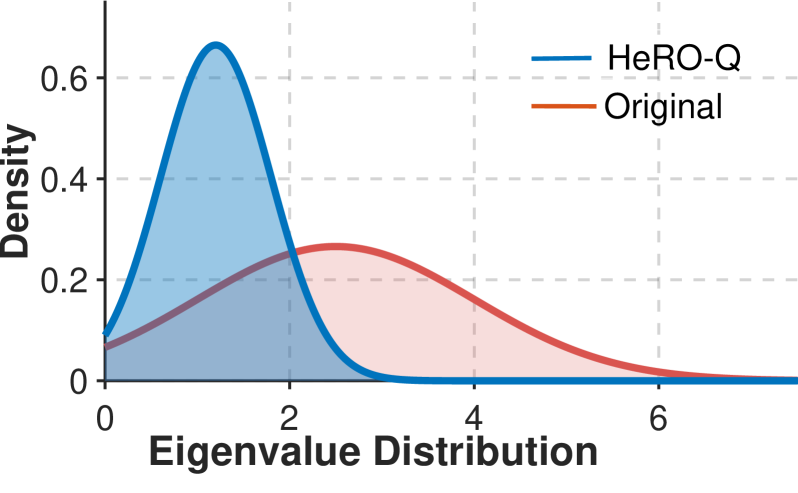
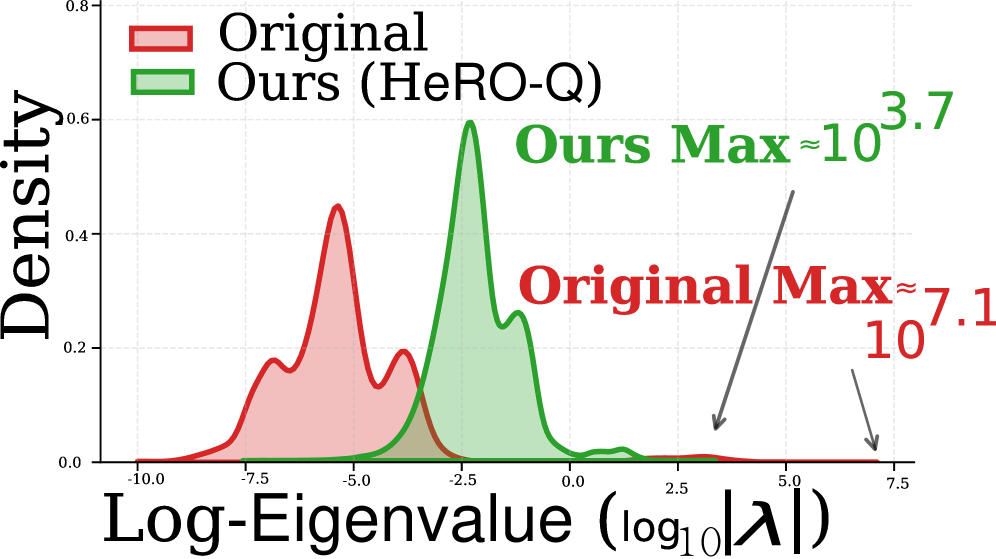
The spectral radius of the Hessian matrix, calculated as the largest singular value, quantifies a model’s sensitivity to input perturbations. A larger spectral radius indicates greater susceptibility to quantization errors because it signifies that the loss function changes rapidly with even small weight adjustments. This is particularly pronounced when a model exhibits a long-tail distribution of weights – meaning a small number of weights have significantly larger magnitudes than the majority – as these large weights disproportionately influence the spectral radius and exacerbate quantization-induced loss increases. Quantization, by reducing the precision of these large weights, introduces larger relative errors, leading to a more substantial impact on the loss function when the spectral radius is high.

Quantization, a technique for reducing model size and accelerating inference, can disproportionately impact weights with high sensitivity within a neural network. Analysis of the loss landscape via the Hessian matrix allows for the identification of these vulnerable weights. The Hessian, representing the second derivatives of the loss function, indicates the curvature of the loss surface; weights located in regions of high curvature are more susceptible to changes induced by quantization. Specifically, a large second derivative along a particular weight dimension signifies that even small perturbations-such as those introduced by reduced precision-can result in a substantial increase in loss. Therefore, examining the Hessian enables targeted protection strategies, such as increased precision or specialized quantization schemes, for the weights most critical to model performance and stability during quantization.

Performance degrades significantly for certain parameters due to noise amplifying along high-curvature directions, akin to how a small perturbation along the short axis of a hyper-ellipsoidal loss landscape-defined by large Hessian eigenvalues-causes a dramatic loss increase, while the same perturbation along the long axis (small eigenvalues) has minimal effect.

Reshaping the Landscape: How HeRo-Q Works

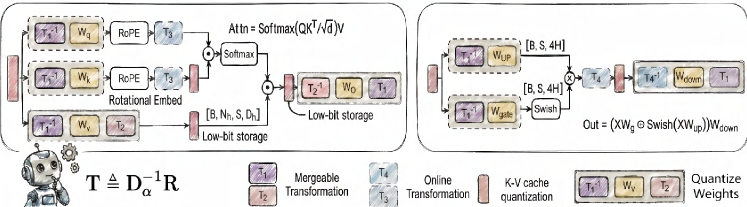
Hessian Robust Quantization (HeRo-Q) builds upon the established technique of Post-Training Quantization (PTQ) by incorporating the Hessian matrix into the quantization process. Traditional PTQ methods often lack awareness of the loss landscape’s curvature, potentially leading to significant accuracy degradation. HeRo-Q addresses this limitation by explicitly analyzing the Hessian, which represents the second-order derivatives of the loss function, to identify directions in the weight space that are particularly sensitive to quantization noise. By considering the Hessian, the framework aims to minimize the impact of quantization on performance, resulting in a more robust and accurate quantized model compared to standard PTQ approaches. This involves assessing the curvature of the loss surface to determine which weights, when quantized, will most negatively impact the model’s output.

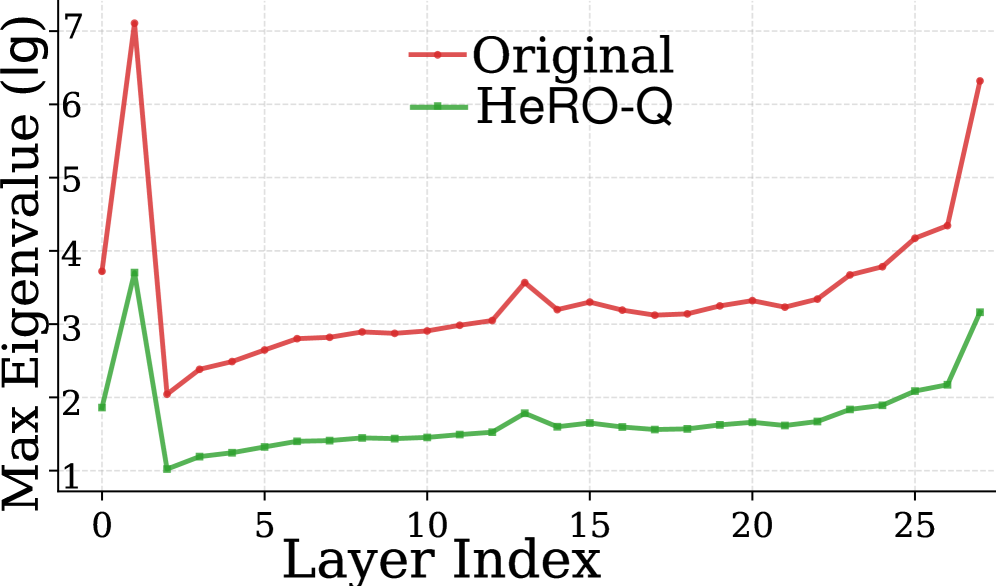
Diagonal Smoothing, as implemented within the Hessian Robust Quantization (HeRo-Q) framework, addresses the issue of quantization sensitivity by reducing the spectral radius of the Hessian matrix. The Hessian, representing the second derivatives of the loss function, identifies directions of high curvature which are particularly susceptible to quantization error. Diagonal Smoothing compresses this spectral radius by applying a damping factor along the diagonal of the Hessian, effectively reducing the magnitude of its eigenvalues. This process diminishes the impact of these highly sensitive directions by decreasing the influence of large eigenvalues, thereby minimizing the variance of quantization noise and improving model robustness post-quantization. The technique focuses on attenuating the most problematic dimensions without requiring full Hessian computation or storage.

Orthogonal Rotation is a core element of Hessian Robust Quantization (HeRo-Q) designed to improve quantization robustness by addressing the issue of quantization noise aligning with dimensions of high sensitivity, as indicated by the Hessian matrix. This technique employs a linear transformation to reshape the Hessian spectrum, effectively redistributing quantization noise across orthogonal dimensions. By minimizing the correlation between quantization noise and these sensitive directions, the impact of quantization on model accuracy is reduced, leading to improved performance at lower precision. The transformation is designed to preserve the overall magnitude of the Hessian’s spectral radius while decorrelating the noise, thus mitigating performance degradation.

Linear transformation is a core component of Hessian Robust Quantization (HeRo-Q), enabling the reshaping of the Hessian spectrum to improve quantization robustness. Specifically, this transformation facilitates the redistribution of quantization noise away from directions of high sensitivity, as indicated by the Hessian’s spectral radius. Evaluation of HeRo-Q on the Llama-3-8B model using W4A16 quantization demonstrates a perplexity of 6.43, representing a performance level closely approaching the full-precision FP16 baseline of 6.41. This indicates the efficacy of the linear transformation in mitigating quantization error and preserving model accuracy.

HeRo-Q effectively equalizes layer-wise spectral radii <span class="katex-eq" data-katex-display="false">\lambda_{max}</span>, mitigating the volatility observed in original models and stabilizing quantization difficulty across all layers. — HeRo-Q effectively equalizes layer-wise spectral radii $\lambda_{max}$ , mitigating the volatility observed in original models and stabilizing quantization difficulty across all layers.

Efficiency Through Simplification

The Fast Walsh-Hadamard Transform (FWHT) provides an efficient mechanism for implementing orthogonal rotations, which are crucial for maintaining performance during quantization. Unlike traditional matrix multiplication-based rotation methods with a complexity of O(N²), the FWHT reduces this to O(N log N) due to its recursive decomposition of the rotation matrix into a series of simpler operations. This computational advantage stems from the FWHT’s reliance on bitwise operations and additions, rather than multiplications, significantly decreasing the number of floating-point operations required. Consequently, using FWHT to perform orthogonal rotations results in substantial speedups and reduced energy consumption, making it well-suited for deployment on hardware with limited computational resources.

Hadamard Rotation minimizes computational expense during orthogonal rotations by leveraging the Fast Walsh-Hadamard Transform. Traditional orthogonal matrices require a significant number of multiply-accumulate operations; however, Hadamard matrices, composed of only +1 and -1 values, allow for replacement of multiplications with additions and subtractions. This substitution substantially reduces the floating-point operations (FLOPs) needed for inference. Consequently, the computational overhead associated with rotation matrices is diminished, leading to a measurable decrease in overall inference costs and enabling deployment on hardware with limited computational resources.

Hessian Robust Quantization (HeRo-Q) enables practical deployment of quantized models in resource-constrained environments due to computational optimizations. Specifically, HeRo-Q demonstrates a quantifiable improvement in model performance; in W4A16 configurations, it achieves up to a 15% improvement in perplexity when compared to standard quantization methods. This performance gain is directly attributable to the reduced computational overhead, making HeRo-Q a viable option for applications where memory and processing power are limited.

Applying HeRo-Q to Llama-1B and Llama-3B models shifts the distribution of Hessian eigenvalues, as demonstrated by the change in log-magnitude density from red (before) to green (after).

Democratizing Access to Powerful Language Models

The process of refining Hessian Robust Quantization relies on a dedicated calibration dataset, which allows for precise parameter tuning to optimize performance. This calibration phase, crucially, requires only 38 minutes to complete – a significant improvement over alternative methods like OmniQuant, which necessitates 72 minutes for the same task. This accelerated calibration not only streamlines the deployment of quantized large language models but also contributes to a more efficient workflow, enabling quicker iterations and faster experimentation with model compression techniques.

The deployment of large language models has historically been constrained by substantial computational demands, limiting their accessibility beyond powerful servers. This framework directly confronts the challenges of model quantization – the process of reducing a model’s precision – to drastically lower these requirements. By successfully quantizing these models, the technology enables their operation on edge devices such as smartphones and embedded systems, and within resource-limited environments where traditional deployment is impractical. This breakthrough expands the possibilities for real-time natural language processing in applications ranging from personalized assistants and localized translation services to offline data analysis and enhanced accessibility tools, effectively bringing the power of large language models to a far wider range of users and use cases.

The development of Hessian Robust Quantization (HeRo-Q) signifies a crucial step towards wider accessibility of large language models. By achieving comparable performance to full-precision (FP16) and GPTQ models while significantly reducing memory requirements – peaking at 24GB of VRAM compared to OmniQuant’s 30GB – HeRo-Q unlocks deployment possibilities previously constrained by hardware limitations. This efficiency extends beyond mere technical specifications; it fosters innovation by enabling the integration of sophisticated natural language processing capabilities into resource-constrained environments, such as edge devices and mobile platforms, and ultimately democratizing access to powerful AI tools for a broader range of developers and applications.

The HeRo-Q inference pipeline employs a hybrid deployment strategy, fusing some transformations <span class="katex-eq" data-katex-display="false"> \mathbf{T}\triangleq\mathbf{D}\_{\alpha}^{-1}\mathbf{R} </span> offline into model weights for zero runtime overhead, while efficiently executing others online with optimized kernels when structural fusion is not possible. — The HeRo-Q inference pipeline employs a hybrid deployment strategy, fusing some transformations $\mathbf{T}\triangleq\mathbf{D}\_{\alpha}^{-1}\mathbf{R}$ offline into model weights for zero runtime overhead, while efficiently executing others online with optimized kernels when structural fusion is not possible.

The pursuit of ever-lower precision, as detailed in HeRo-Q’s reshaping of the loss landscape via Hessian conditioning, feels predictably optimistic. The paper attempts to redistribute quantization noise, essentially smoothing out the inevitable bumps. One recalls the words of Henri Poincaré: “Mathematics is the art of giving reasons.” This framework, while mathematically elegant in its approach to spectral compression, operates under the assumption that reason can consistently tame the chaos of production data. Tests will reveal whether this attempt to engineer robustness truly holds against the unpredictable realities of deployment, or if it simply delays the inevitable accumulation of tech debt. The spectrum may be compressed, but Mondays always arrive.

What’s Next?

The pursuit of ever-lower precision continues, predictably. HeRo-Q offers another reshaping of the loss landscape, another attempt to coax performance from increasingly constrained models. It’s a sensible enough approach – manipulating the Hessian spectrum sounds impressive, and spectral compression is always a good buzzword for a conference submission. But the inevitable truth remains: each elegant fix introduces a new set of sensitivities. Production environments aren’t pristine testbeds; they’re collections of edge cases and unanticipated data drift. The reported gains will, undoubtedly, require further refinement-and likely, a dedicated team to debug the inevitable regressions when deployed at scale.

Future work will almost certainly focus on adaptive Hessian conditioning, attempting to automate the reshaping process. Perhaps a neural network to learn the optimal compression strategy? It’s a reasonable direction, but one should remember that complexity rarely decreases in the long run. The real challenge isn’t achieving low-bit inference in a controlled setting; it’s maintaining that performance when the data decides to be uncooperative. If the code looks perfect, no one has deployed it yet.

The field will also need to grapple with the hardware implications. These techniques aren’t free; they add computational overhead. The benefits of reduced memory footprint must outweigh the cost of manipulating the Hessian. It’s a classic trade-off, and one often glossed over in the rush to publish. The pursuit of efficiency is a cycle: refine, deploy, discover new bottlenecks, repeat.

Original article: https://arxiv.org/pdf/2601.21626.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/