Quantum Decoding Gets a Boost from Channel Eigenlists

Author: Denis Avetisyan

A new analysis technique leveraging the structure of quantum channels promises more efficient decoding algorithms for critical error-correcting codes.

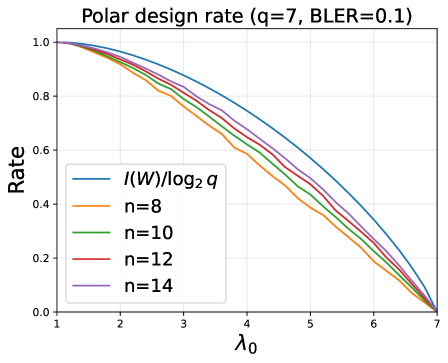
The study demonstrates the relationship between block length and the decoding rate <span class="katex-eq" data-katex-display="false">\frac{|\mathcal{A}|}{N}</span> for polar codes, illustrating how performance scales with increasing code size. — The study demonstrates the relationship between block length and the decoding rate $\frac{|\mathcal{A}|}{N}$ for polar codes, illustrating how performance scales with increasing code size.

This work introduces a method for analyzing and designing quantum decoders for symmetric pure-state channels by utilizing the channel’s Gram matrix eigenlist to enable efficient density evolution and fidelity bounds for polar and LDPC codes.

Efficient decoding over noisy quantum channels remains a central challenge, particularly as communication protocols move beyond binary systems. This paper, ‘Belief Propagation with Quantum Messages for Symmetric Q-ary Pure-State Channels’, introduces a generalized framework for analyzing belief propagation with quantum messages (BPQM) applicable to symmetric q-ary pure-state channels, leveraging the channel’s Gram matrix eigenlist to derive closed-form recursions for density evolution. These recursions yield explicit BPQM unitaries and analytic fidelity bounds, enabling the estimation of decoding thresholds for low-density parity-check (LDPC) codes and the construction of polar codes. Will this approach unlock more robust and efficient quantum communication systems for increasingly complex channel structures?

The Inevitable Noise: Confronting the Limits of Classical Communication

The transmission of information invariably encounters noise, demanding robust coding schemes to ensure reliable communication. However, conventional error-correction codes, meticulously designed for the predictable disturbances of classical channels, prove surprisingly inadequate when applied to the fundamentally different landscape of quantum communication. Quantum information, encoded in fragile states like superposition and entanglement, is easily disrupted by even minor interactions with the environment. This susceptibility stems from the no-cloning theorem, which prohibits the simple replication of unknown quantum states – a cornerstone of classical redundancy. Consequently, classical codes, reliant on creating multiple copies of a message for error detection, cannot be directly translated to the quantum realm. Instead, researchers are actively developing specialized quantum error-correcting codes that leverage the principles of quantum mechanics – such as entanglement and superposition – to protect information without violating fundamental laws, pushing the boundaries of what’s possible in secure and reliable communication.

Quantum information, encoded in the delicate states of qubits, is profoundly susceptible to environmental noise and disturbance – a stark contrast to the robustness of classical bits. This inherent fragility stems from the principles of quantum mechanics; any attempt to measure or observe a qubit’s state inevitably alters it, introducing errors during transmission. Consequently, traditional error-correction strategies designed for classical communication prove largely ineffective. Protecting quantum messages demands innovative approaches, such as quantum error-correcting codes that distribute quantum information across multiple entangled qubits – creating redundancy without violating the no-cloning theorem. These codes don’t simply copy the information, but rather encode it in a way that allows errors to be detected and corrected without directly measuring the fragile quantum state, paving the way for reliable long-distance quantum communication and computation.

Classical error-correcting codes, designed for the robustness of bits, prove surprisingly inadequate when applied to the transmission of quantum information. This stems from the fundamental difference in how errors manifest: classical bits are either flipped or remain unchanged, while quantum states can be subtly corrupted in infinitely many ways due to the continuous nature of quantum information. Consequently, codes that maximize the rate of reliable communication in the classical realm often fall short when attempting to protect fragile quantum states from decoherence and noise. The limitations arise because these classical codes aren’t optimized for the unique challenges posed by quantum mechanics – specifically, the no-cloning theorem prevents simple replication for redundancy, and measurements inherently disturb the quantum state. This necessitates the development of entirely new quantum codes, like those leveraging entanglement and superposition, to approach the theoretical limits of reliable quantum communication – a rate governed by the quantum channel capacity and the inherent properties of quantum information itself.

Density Evolution: A Rigorous Framework for Decoder Analysis

Density evolution analyzes the iterative decoding process by tracking the probability density function (PDF) of the exchanged messages. These messages, representing beliefs about transmitted bits, are passed between variable (bit) nodes and check nodes in a graphical model. The algorithm models how these PDFs evolve with each iteration, quantifying the information passed between nodes. Specifically, it examines the mean and variance of these probability distributions to determine if the decoding process converges – that is, whether the estimated probabilities become increasingly accurate, leading to correct decoding. By observing the shape of these evolving PDFs, density evolution predicts the performance of iterative decoders without requiring extensive simulations of the decoding process.

Density evolution predicts the performance of iterative decoding algorithms by tracking the statistical evolution of probabilistic messages exchanged between decoder nodes. Specifically, it models how the marginal distribution of the belief in each bit’s value changes with each iteration of the decoding process. If, as iterations continue, these distributions converge to a peaked shape around the transmitted value, reliable decoding is predicted; conversely, if the distributions broaden or fail to converge, decoding is likely to fail. This predictive capability allows engineers to determine the maximum achievable data rate – the threshold – for a given code and channel combination, without requiring extensive simulations or actual transmission experiments.

The precision of density evolution analysis is fundamentally linked to a detailed understanding of the code’s graphical structure, particularly the connectivity between bit nodes and check nodes. Low-Density Parity-Check (LDPC) codes, for example, are defined by their sparse parity-check matrices, and the degree distributions of the corresponding bit and check nodes directly influence the convergence behavior of the decoding algorithm. Accurate determination of these degree distributions is essential for calculating the density evolution threshold – the maximum ratio of transmitted bits to noise level at which reliable decoding is possible. This threshold is determined by tracking the evolution of probability densities as they propagate through the graph, and any inaccuracies in modeling the node relationships will lead to an incorrect threshold prediction and potentially unreliable decoding performance.

Channel Fidelity and the Gram Matrix: Quantifying the Degradation of Quantum States

Channel fidelity, denoted as $F$ , quantifies the degree to which a quantum channel preserves the state of an input quantum state. It is mathematically defined as the maximum overlap between the output of the channel acting on any input state and that state itself. Specifically, if $\mathcal{N}[ρ]$ represents the effect of a quantum channel on a density matrix ρ, then $F = max_{ρ} <ρ, \mathcal{N}[ρ]>$ , where the inner product represents the trace. A fidelity of 1 indicates perfect state preservation, while a lower fidelity signifies a greater degree of information loss during transmission. This metric is crucial for characterizing channel performance and is utilized in evaluating the effectiveness of quantum error correction schemes and the feasibility of quantum communication protocols.

The Gram matrix, constructed from an arbitrary quantum channel $\mathcal{N}$ , provides a complete characterization of the channel’s action on quantum states. Specifically, the elements of the Gram matrix are given by $G_{ij} = \langle \psi_i | \mathcal{N} | \psi_j \rangle$ , where $| \psi_i \rangle$ and $| \psi_j \rangle$ represent input states. This matrix fully determines the channel’s ability to preserve the distinguishability of quantum states; a larger determinant of the Gram matrix indicates a higher degree of information preservation. Analysis of the Gram matrix allows for the calculation of important channel properties like fidelity and provides a means to quantify the impact of noise on transmitted quantum information, enabling detailed assessment of channel capacity and performance.

The relationship between channel fidelity and the Gram matrix enables the construction of quantum error-correcting codes tailored to specific noise characteristics. Analysis reveals that the fidelity of a combined channel, represented as $F(W1 ⧆ W2)$ , where $W1$ and $W2$ are individual channel transformations, is upper-bounded by $F(W1 ⧆ W2) \leq (q-1)F(W1)F(W2)$ . Here, $q$ represents the dimension of the quantum system. This bound is crucial for evaluating the performance limits of concatenated codes and provides a quantifiable target for code design aimed at maximizing information recovery in the presence of noise. The fidelity metric, therefore, serves not only as a diagnostic tool but also as a parameter in optimizing code performance against defined channel characteristics.

Decoded Quantum Interferometry: Reversing the Effects of Noise Through Interference

Decoded Quantum Interferometry (DQI) represents a class of decoding algorithms that leverages interference phenomena to efficiently determine the most likely transmitted quantum state. Unlike traditional decoding methods reliant on complex optimization procedures, DQI recasts the decoding problem as a series of reversible quantum operations. This approach utilizes a network of quantum gates to propagate information about the received syndrome, ultimately producing an estimate of the original quantum message. The efficiency gains stem from the ability to perform multiple syndrome checks in parallel and the inherent reversibility of the operations, potentially reducing the computational complexity associated with quantum error correction, particularly for codes with structured decoding graphs.

Decoded Quantum Interferometry (DQI) facilitates quantum error correction by transforming computationally intensive optimization problems into reversible decoding problems. Traditional decoding often requires finding the most likely transmitted data given a noisy received state – a complex optimization task. DQI achieves this by mapping the error correction process onto a series of unitary transformations, effectively reversing the effects of the noise channel. This reversal is possible due to the inherent properties of quantum mechanics and allows for the reconstruction of the original quantum state without requiring computationally expensive searches for optimal solutions. Consequently, DQI opens avenues for implementing more efficient and scalable quantum error correction schemes, particularly for codes where direct decoding algorithms are impractical.

The performance of iterative decoding algorithms, such as those employed in Decoded Quantum Interferometry (DQI), is rigorously assessed through density evolution, a technique that tracks the probability distributions of errors as they propagate through the decoder. This analysis allows for the determination of decoding thresholds – the maximum channel error rate at which reliable decoding is still possible. Specifically, these thresholds are estimated for given combinations of variable node degree ( $d_v$ ) and check node degree ( $d_c$ ), providing a quantitative measure of decoder performance under different channel conditions. Accurate determination of these thresholds requires careful consideration of channel fidelity, as even slight deviations from ideal conditions can significantly impact decoding success.

Towards Practical Quantum Communication: Optimizing Codes for Real-World Channels

Quantum error correction relies on meticulously crafted code structures and efficient decoding algorithms, yet current designs often lack optimization for the nuances of real-world quantum channels. Unlike the idealized conditions frequently assumed in theoretical models, practical quantum communication is susceptible to a variety of noise sources – each with unique statistical properties. Consequently, significant research focuses on tailoring codes not just for general noise reduction, but for specific channel characteristics, such as depolarization, amplitude damping, or phase flip. This involves exploring novel code families beyond established options like surface codes or topological codes, as well as developing decoding strategies that effectively leverage information about the channel’s noise profile. Achieving this level of optimization is crucial for minimizing error rates and maximizing the fidelity of quantum information transfer, ultimately enabling the realization of robust and dependable quantum communication networks.

A promising avenue for refining quantum error correction lies in the synergistic application of Fourier vector analysis and density evolution. This computational technique allows researchers to rigorously assess the performance of various quantum codes – notably, polar codes – as they transmit information through noisy quantum channels. Recent analyses demonstrate that polar codes, when engineered to achieve a specific Block Error Rate, increasingly approach the theoretical Shannon limit – the channel capacity – as the code’s block length grows. This convergence suggests that through careful code design and optimization using these analytical tools, highly efficient and reliable quantum communication becomes increasingly attainable, pushing the boundaries of what’s possible in secure data transmission and quantum networking.

The pursuit of optimized quantum error-correcting codes directly fuels the development of practical, secure communication networks. While quantum key distribution offers theoretical security, its real-world implementation demands robust codes capable of mitigating the inevitable noise present in quantum channels. Continued refinement of these codes, alongside advancements in decoding techniques, promises to overcome current limitations in transmission distance and data rates. Successfully establishing these networks will not only revolutionize data security through unhackable communications but also enable distributed quantum computing and the secure transfer of sensitive information, ushering in a new era of information technology underpinned by the principles of quantum mechanics.

The pursuit of optimal decoding, as detailed in this exploration of belief propagation with quantum messages, echoes a fundamental tenet of mathematical rigor. The article’s focus on leveraging the channel’s Gram matrix eigenlist to achieve efficient density evolution and fidelity bounds exemplifies this principle. It’s a commitment to understanding the inherent structure of the communication channel, not merely observing empirical performance. As G. H. Hardy observed, “Mathematics may not teach us how to add love or minus hate, but it gives us the tools to quantify and understand the world around us.” This resonates deeply with the presented work; the pursuit isn’t simply about making a decoder function, but about building a provably sound and elegant decoding algorithm, grounded in the mathematics of quantum information theory.

Beyond the Eigenlist: Charting a Course for Quantum Decoding

The present work, while establishing a rigorous framework for analyzing quantum decoding via the channel’s Gram matrix eigenlist, merely scratches the surface of a fundamental difficulty. The elegance of deriving fidelity bounds and enabling density evolution is not, in itself, a solution. It is a precisely defined problem. The true challenge remains: extending this approach beyond symmetric, pure-state channels. The current reliance on spectral properties, while mathematically satisfying, feels… limited. It invites the question of whether a truly general decoding algorithm can be constructed solely from linear algebra, or if fundamentally different principles are required to address the complexities of mixed states and depolarizing noise.

Further exploration must address the computational cost of eigenlist recursion, particularly as channel dimensions increase. The current method, while theoretically sound, risks becoming intractable for practical code lengths. A simplification – not merely an approximation, but a provably equivalent reformulation – would be a significant advance. The pursuit of such simplicity does not equate to brevity; it demands non-contradiction and logical completeness. A fleeting performance gain, achieved through heuristic methods, is ultimately unsatisfying.

One intriguing, though perhaps distant, avenue lies in exploring connections between this eigenlist-based approach and the emerging field of quantum machine learning. Could a learned representation of the channel, derived from its eigenlist, facilitate the design of more robust and efficient decoders? It is a question worth considering, provided it is approached with the same demand for mathematical rigor that underpins the present investigation. Anything less would be… aesthetically displeasing.

Original article: https://arxiv.org/pdf/2601.21330.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/