Beyond Black Boxes: Architecting Trustworthy Cyber-Physical Systems

Author: Denis Avetisyan

A new approach to system design leverages independent, validated models and real-time monitoring to guarantee state integrity and overcome the limitations of traditional machine learning.

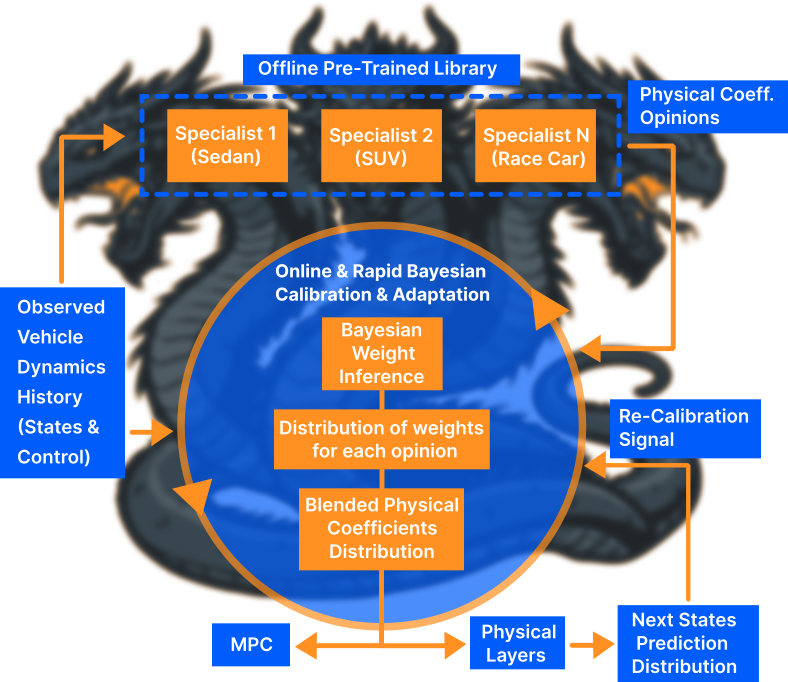
The system architecture decouples a static, foundational “Constitution” - embodied here as a library of specialist algorithms - from dynamic, online governance implemented via Bayesian methods like variational inference, enabling jurisdictional shifts without the need for exhaustive retraining when faced with evolving operational conditions or regime drifts. — The system architecture decouples a static, foundational “Constitution” – embodied here as a library of specialist algorithms – from dynamic, online governance implemented via Bayesian methods like variational inference, enabling jurisdictional shifts without the need for exhaustive retraining when faced with evolving operational conditions or regime drifts.

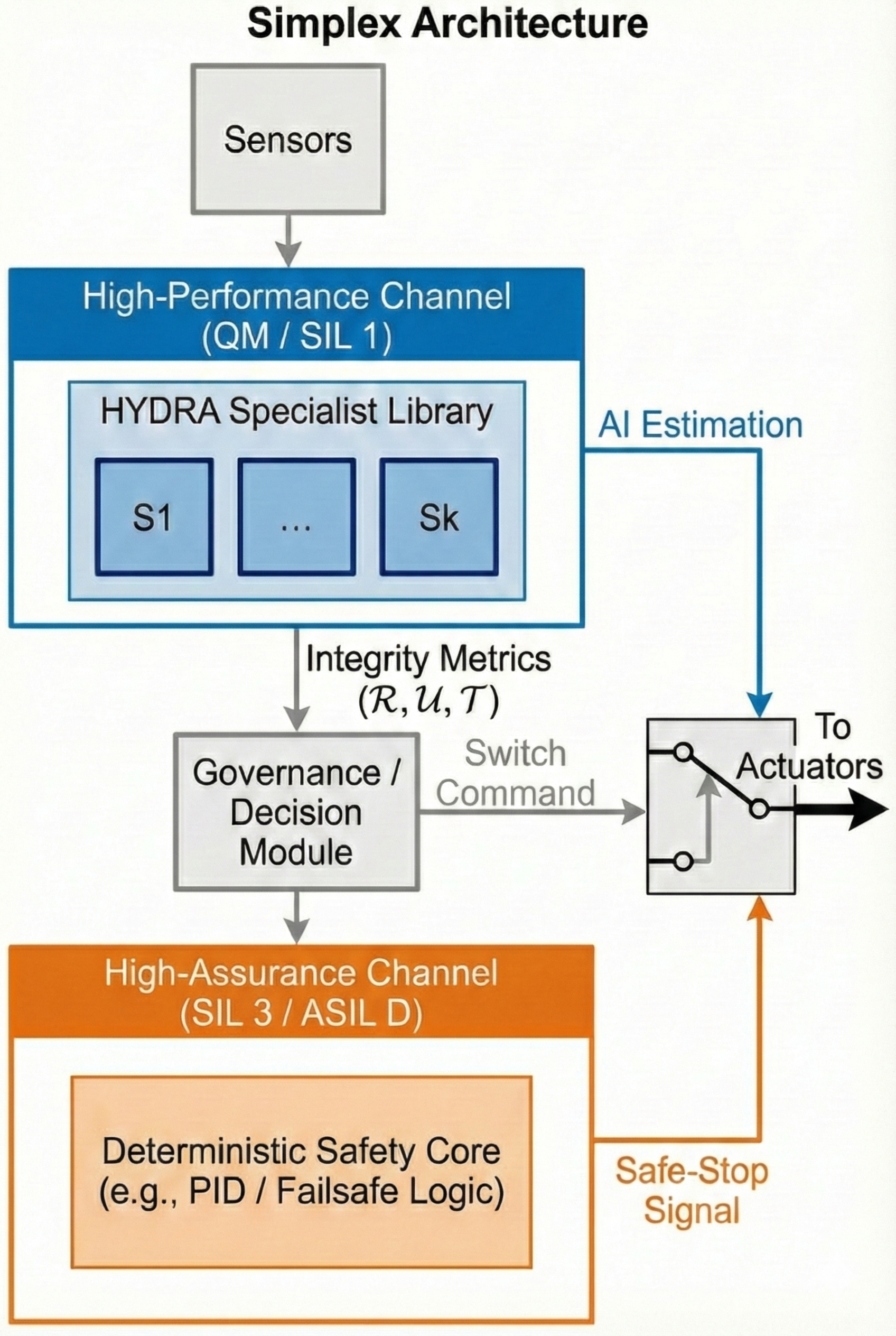
Modular Sovereignty provides a certifiable framework for managing the plasticity-stability paradox in complex cyber-physical systems using runtime residuals and polytopic LPV models.

Despite advances in machine learning for time-series and physical dynamics, deploying these models in safety-critical Cyber-Physical Systems (CPS) remains challenged by catastrophic forgetting, spectral bias, and opacity-hindering certifiable reliability. This position paper, ‘Position: Certifiable State Integrity in Cyber-Physical Systems — Why Modular Sovereignty Solves the Plasticity-Stability Paradox’, argues that overcoming the plasticity-stability paradox requires moving beyond global parameter updates. We propose ‘Modular Sovereignty’-a library of frozen, regime-specific specialists blended with uncertainty-aware weighting-to ensure certifiable state integrity across the CPS lifecycle. Could this paradigm shift enable a new generation of robust, auditable, and demonstrably safe autonomous systems?

The Illusion of Universal Models

Despite remarkable advancements, universal foundation models exhibit limitations when applied to the complex and varied world of Cyber-Physical Systems (CPS). These models, trained on broad datasets, often falter when reasoning about the unique dynamics and constraints of physical systems – from robotic control and autonomous vehicles to smart grids and manufacturing processes. The core issue lies in the disparity between the data distribution encountered during training and the real-world complexities of CPS, where nuanced interactions between software and physical components demand a level of contextual understanding and adaptive reasoning that generalized models frequently lack. Consequently, deploying these models ‘off-the-shelf’ in critical CPS applications can lead to unpredictable behavior, safety concerns, and diminished performance, highlighting the need for specialized adaptation techniques or entirely new modeling paradigms tailored to the intricacies of the physical world.

Universal foundation models, despite their impressive capabilities, face a fundamental trade-off between plasticity and stability, significantly impacting their reliability in real-world applications. This dilemma arises because adapting to new, unseen cyber-physical systems – a core requirement for generalization – necessitates modifying the model’s internal representations, potentially disrupting previously learned knowledge. Compounding this issue is an inherent spectral bias, where these models disproportionately rely on low-frequency components of data, hindering their ability to capture the high-frequency, often crucial, dynamics present in complex physical processes. Consequently, while scaling model size can improve performance on benchmark datasets, it doesn’t inherently resolve this representational bottleneck, leaving these systems vulnerable to unpredictable behavior and reduced trustworthiness when deployed in critical infrastructure, robotics, or autonomous vehicles.

Increasing the scale of universal foundation models, while a common strategy for enhancing performance, encounters diminishing returns when applied to complex systems. Simply adding more parameters doesn’t fundamentally address the core issue of representational capacity – the ability to effectively capture and generalize across the vast and varied data inherent in real-world cyber-physical systems. While scaling improves pattern recognition within the training distribution, it often fails to yield proportionate gains in true understanding or robust reasoning in novel scenarios. This is compounded by substantial computational demands; the energy and resource costs associated with training and deploying these increasingly large models present significant practical barriers, suggesting that alternative approaches focused on architectural innovation and data efficiency may be crucial for overcoming inherent limitations and achieving reliable performance in critical applications.

Modular Sovereignty: A Shift in System Design

Modular Sovereignty establishes a system-building methodology centered on the decomposition of complex tasks into discrete, specialized models. This contrasts with monolithic approaches where a single model handles all functions; instead, Modular Sovereignty advocates for independent modules, each responsible for a specific sub-task. This decomposition facilitates targeted development, verification, and maintenance of individual components. The framework’s emphasis on modularity allows for the creation of systems where each module’s functionality and limitations are clearly defined, contributing to improved overall system robustness and predictability. This architectural pattern enables independent certification of each module, simplifying the process of demonstrating system-wide safety and reliability.

Monolithic models, due to their inherent complexity and interconnectedness, present significant challenges for comprehensive verification and validation. The difficulty in isolating failure points within a single, large model increases the probability of undetected errors, potentially leading to catastrophic system failures. Modular approaches mitigate this risk by decomposing the overall task into smaller, independent modules. This decomposition facilitates rigorous testing and certification of each module in isolation, allowing for the identification and correction of errors before system integration. By limiting the scope of potential failures to individual modules, the overall system exhibits increased robustness and a substantially reduced risk of widespread, critical failures compared to monolithic architectures.

Modular Sovereignty facilitates system composability and targeted updates by establishing well-defined jurisdictional boundaries and interfaces between specialized models. This architecture contrasts with monolithic designs, allowing for individual model refinement or replacement without necessitating complete system retraining. A key objective is the reduction of false positive rates; this is achieved through explicit signaling of ‘manifold exits’ – clearly defined points where a model’s scope ends – and the implementation of safety integrity decomposition, which systematically allocates safety-critical functions to specific, verifiable modules. This decomposition isolates potential failure points and simplifies the validation process, contributing to improved overall system reliability.

HYDRA: Formal Verification Through Geometry

HYDRA employs RPI Zonotopes – a method for representing sets of real vectors – to model system states and their associated uncertainties. This representation allows for the formal verification of system properties by propagating these uncertainties through computations. Coupled with Bayesian Inference, HYDRA can quantify the probability of a system satisfying specific requirements, even in the presence of noise or incomplete information. This approach enables rigorous verification by providing probabilistic guarantees on system behavior, differing from traditional methods that often rely on worst-case assumptions or lack quantifiable robustness metrics. The combination of RPI Zonotopes and Bayesian Inference forms the core of HYDRA’s ability to provide verifiable and reliable system operation within defined probabilistic bounds.

HYDRA utilizes RPI Zonotopes to represent system states as a means of formally quantifying uncertainty. A Zonotope is a set-based representation constructed by taking the Minkowski sum of a center point and affine generators. This allows HYDRA to encapsulate the range of possible system states given inherent noise or imprecise inputs. By propagating these Zonotopes through system dynamics, HYDRA can over-approximate the reachable set of states, thereby providing formal guarantees of robustness. Specifically, if the desired safe set is disjoint from the over-approximation, the system is guaranteed not to enter the unsafe region within the bounds of the modeled uncertainty; this is achieved without requiring explicit probabilistic modeling of uncertainty, instead relying on the set-based representation of $\mathbb{R}^n$ .

HYDRA’s adaptability and performance are enhanced through the integration of Physics-Informed Machine Learning and Generative Meta-Learning techniques. A key component of this efficiency is the ‘Constitutional Greedy Accretion Protocol’, which minimizes the size of the specialist library – denoted as K – relative to the overall system dimensionality. This protocol ensures that $K << \text{dimensionality}$ , resulting in a compact representation that facilitates efficient runtime execution and reduces computational overhead. The library’s minimized size is crucial for scalability and real-time verification within the HYDRA framework.

The Limits of Abstraction: Geometric Guarantees in Practice

HYDRA leverages the power of computational geometry, specifically utilizing concepts like Convex Hulls and Zonotopes, to establish a robust foundation for formal verification of complex systems. A Convex Hull encapsulates the reachable set of states a system can attain given uncertainties, providing a conservative but mathematically rigorous bound. Zonotopes, extending this idea, represent uncertainty as a linear combination of vectors, allowing for a more refined and efficient representation of state spaces. This geometric approach transforms the problem of verifying safety and performance into one of determining set inclusion – whether a potentially hazardous region lies outside the system’s defined operational boundaries. By representing system states and uncertainties geometrically, HYDRA facilitates the application of powerful formal methods and algorithms, enabling the provision of provable guarantees regarding system behavior even in the face of unpredictable conditions.

HYDRA leverages geometric principles to move beyond simply detecting potential system failures and instead provides a means to rigorously quantify uncertainty. By representing system states and allowable deviations within geometric shapes – like convex hulls and zonotopes – the framework establishes a formal basis for analyzing worst-case scenarios. This geometric representation isn’t merely descriptive; it allows for the calculation of bounds on system behavior, enabling provable safety guarantees. Consequently, designers can demonstrate – with mathematical certainty – that a system will remain stable and perform as expected, even when faced with disturbances or imprecisely known parameters. The resulting certifications are not based on extensive testing alone, but on formal verification techniques that provide a higher degree of confidence in system reliability and performance under a defined set of conditions.

HYDRA’s capabilities are significantly broadened through the incorporation of Linear Parameter-Varying (LPV) systems, allowing it to address a more diverse set of control and optimization challenges. This integration isn’t simply about expanding the problem domain; it’s about ensuring robust and predictable behavior as the system transitions between different operating modes, managed by specialized control algorithms. To achieve this, HYDRA implements carefully designed dwell time constraints – minimum time intervals required before switching between these specialists. These constraints are crucial for preventing high-frequency oscillations, often termed ‘chattering’, which can compromise stability and performance. More importantly, they guarantee a decisive transition during regime shifts, ensuring the system reliably adopts the new control strategy without lingering in an unstable intermediate state. This focus on handover stability is a key differentiator, enabling HYDRA to handle complex systems with dynamic and potentially unpredictable behavior.

Simplex integration ensures AI (<span class="katex-eq" data-katex-display="false">QM</span>) remains isolated from safety-critical systems (<span class="katex-eq" data-katex-display="false">ASIL\ D</span>) by utilizing specialist estimation and a high-assurance fallback channel governed by a dedicated controller, as visualized with GenAI assistance. — Simplex integration ensures AI ( $QM$ ) remains isolated from safety-critical systems ( $ASIL\ D$ ) by utilizing specialist estimation and a high-assurance fallback channel governed by a dedicated controller, as visualized with GenAI assistance.

Beyond the Hype: Towards Resilient Time-Series Analysis

Despite the recent successes of Transformer-based models and large language models like TimeGPT in analyzing time-series data, inherent limitations are driving research into alternative architectures. These powerful models often struggle with long-range dependencies and can be computationally expensive, hindering their application to extensive datasets or real-time forecasting. Consequently, innovative approaches such as TimesFM and DeepONet are gaining traction. TimesFM leverages frequency-domain analysis to efficiently capture periodic patterns, while DeepONet, a neural operator, offers a data-driven method for learning continuous mappings between function spaces, potentially generalizing beyond observed data. These alternatives aim to address the scalability and generalization challenges faced by traditional methods, paving the way for more robust and efficient time-series analysis.

Neural Operators represent a significant departure from traditional time-series analysis by treating functions – the mappings from time to value – as the primary objects of study. Instead of learning parameters within a fixed model architecture, these operators learn the underlying relationship between input and output functions directly, offering the potential to generalize to unseen dynamics and extrapolate further into the future. However, this functional learning paradigm introduces unique challenges regarding reliability and verification. Unlike standard machine learning models assessed through metrics on finite datasets, validating a Neural Operator requires demonstrating its consistency and stability across the entire function space. Current research focuses on developing techniques – including rigorous error bounds and sensitivity analysis – to ensure these operators don’t produce spurious or physically implausible predictions, particularly when dealing with chaotic or high-dimensional systems, and ultimately establishing trust in their long-term forecasting capabilities.

The progression of time-series analysis is increasingly focused on synergistic combinations of established and emerging methodologies. Rather than relying on singular, monolithic models, researchers are investigating hybrid systems that leverage the benefits of modularity – breaking down complex problems into manageable components – alongside geometric reasoning, which allows for the capture of underlying structural relationships within the data. These modular, geometrically-informed frameworks are then further enhanced by advanced machine learning techniques, such as neural operators and transformer architectures, to refine predictions and improve generalization. This convergence isn’t merely about stacking algorithms; it’s about creating systems where each component complements the others, resulting in models that are both more accurate and demonstrably resilient to the inherent noise and variability found in real-world time-series data. Ultimately, this integrated approach promises to unlock a new level of performance and reliability in forecasting and anomaly detection across diverse applications.

The pursuit of certifiable state integrity in cyber-physical systems, as detailed in this work, inevitably circles back to the fundamental tension between plasticity and stability. It’s a familiar dance; elegant architectures proposed to solve today’s problems become tomorrow’s rigid bottlenecks. One could almost anticipate this outcome. As Paul Erdős famously stated, “A mathematician knows a lot of things, but he doesn’t know everything.” The same holds true for system designers. This ‘Modular Sovereignty’ approach, with its library of validated models governed by runtime residuals, is a pragmatic acknowledgement of this limitation. It’s not about achieving perfect foresight, but about containing the inevitable entropy through a well-defined, auditable decomposition. The idea of isolating failures within these ‘Sovereigns’ suggests a healthy dose of cynicism – anticipating, and preparing for, the fact that something will eventually go wrong.

What’s Next?

The pursuit of ‘certifiable’ anything in Cyber-Physical Systems invariably reveals the cost of guarantees. This work, with its ‘Modular Sovereignty’ and runtime residuals, offers a structured way to manage complexity, but does not eliminate it. Each ‘Sovereign’ module, however meticulously validated, introduces another surface for failure, another integration point where assumptions may crumble. The elegance of the proposed architecture will, inevitably, be tested by the realities of deployment – by the edge cases no simulation fully anticipates, and by the relentless drive to squeeze more performance from limited hardware.

Future work will likely focus on automating the verification of these modular components, and on developing robust methods for composing them. The question isn’t simply can a system be certified, but at what cost, and how often must that certification be renewed as the system evolves? The promise of physics-informed machine learning, while appealing, shouldn’t overshadow the fact that all models are approximations, and all approximations degrade over time. The tooling around runtime residual analysis will prove crucial, but the true measure of success won’t be the sophistication of the diagnostics, but the speed with which problems are actually fixed.

It’s worth remembering that a beautifully architected system is often just an expensive way to complicate everything. If the code looks perfect, no one has deployed it yet. The real challenge lies not in achieving theoretical certifiability, but in building systems that are demonstrably reliable – and that requires a healthy dose of skepticism, a willingness to embrace imperfection, and a well-stocked bug tracker.

Original article: https://arxiv.org/pdf/2601.21249.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/