Decoding Quantum Noise: A New Entropy Framework for Secure Communication

Author: Denis Avetisyan

Researchers have developed a unified approach to understanding and quantifying noise in quantum communication channels, paving the way for more robust and secure data transmission.

Hybrid quantum noise is characterized through a differential entropic function and a quantum Rényi entropic function, both modeled in three dimensions using Gaussian Mixture Models to reveal its complex, multi-dimensional structure.

This review demonstrates the equivalence of collision and differential entropy for finite-regime Quantum Key Distribution in hybrid quantum noisy channels, leveraging Gaussian mixture models for improved security analysis.

Quantifying uncertainty in quantum communication channels is often complicated by the presence of mixed discrete and continuous noise. This is addressed in ‘Comparative Analysis of Differential and Collision Entropy for Finite-Regime QKD in Hybrid Quantum Noisy Channels’, which investigates the relationship between differential, Rényi, and collision entropies within hybrid quantum channels modeled using Gaussian mixture models. The research demonstrates that, under specific conditions, differential and collision entropy become equivalent, offering a unified framework for analyzing uncertainty and impacting secure key rates in quantum key distribution. Will this unified perspective pave the way for more robust and efficient quantum communication protocols in increasingly complex noisy environments?

The Uncertainty at the Heart of Quantum Information

The principles governing classical information, built on the certainty of defined states, falter when applied to the quantum realm. Quantum systems inherently exist in superpositions and are governed by probability, introducing an irreducible uncertainty that classical information theory cannot adequately address. This isn’t simply a matter of lacking complete knowledge; the uncertainty is fundamental to the nature of quantum states themselves. Consequently, new mathematical tools are essential to quantify this inherent ambiguity and accurately describe information processing within quantum systems. Attempts to force classical measures onto quantum phenomena lead to inconsistencies and fail to capture the unique properties like entanglement and quantum coherence, necessitating a complete rethinking of how information is defined and measured at the quantum level.

Quantum systems, unlike their classical counterparts, exist in states defined by probabilities that don’t simply describe a lack of knowledge, but are fundamental to their nature. Consequently, classical information theory proves inadequate for describing and quantifying information within these systems. Quantum entropy provides the necessary mathematical framework to address this challenge, extending concepts like Von Neumann entropy – analogous to Shannon entropy in classical information theory – to capture the unique properties of quantum states. $S = -Tr(\rho log_2 \rho)$ This allows researchers to not only measure the uncertainty inherent in a quantum state ρ, but also to understand how information is encoded and manipulated within it, laying the groundwork for advancements in quantum computation and communication. By characterizing the inherent randomness of quantum systems, quantum entropy becomes an essential tool for harnessing their potential.

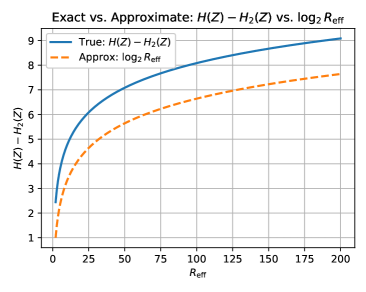
Refining the measurement of uncertainty in quantum systems requires tools beyond standard entropy calculations. Researchers have turned to generalizations of entropy, notably Rényi Entropy, and its specialized form, Collision Entropy, to achieve increasingly precise quantification of quantum information. A recent study reveals a practical approximation for differential entropy, demonstrating that $H(Z) \approx H_2(Z) + log_2(Reff)$ yields accurate results. This simplification, where $H(Z)$ represents differential entropy and $H_2(Z)$ is a specific Rényi Entropy, offers a computationally efficient method for assessing uncertainty, effectively bridging the gap between theoretical precision and practical application in quantum information processing and communication.

The quantum collision entropic function of HQN, represented in 3D, demonstrates that its logarithmic approximation <span class="katex-eq" data-katex-display="false">\log_2 R_{\text{eff}}</span> accurately estimates the true value <span class="katex-eq" data-katex-display="false">H(Z) - H_2(Z) = \log_2 R_{\text{eff}} + \frac{d}{2} \log_2 e</span>-remaining within a 10% error threshold-and converges as the effective rank <span class="katex-eq" data-katex-display="false">R_{\text{eff}}</span> increases, validating its use in high-rank regimes. — The quantum collision entropic function of HQN, represented in 3D, demonstrates that its logarithmic approximation $\log_2 R_{\text{eff}}$ accurately estimates the true value $H(Z) - H_2(Z) = \log_2 R_{\text{eff}} + \frac{d}{2} \log_2 e$ -remaining within a 10% error threshold-and converges as the effective rank $R_{\text{eff}}$ increases, validating its use in high-rank regimes.

The Fragility of Quantum Signals: Noise as an Inevitable Reality

Quantum communication systems, while theoretically secure, are susceptible to degradation from quantum noise introduced by real-world limitations. This noise originates from multiple sources within the communication channel and the apparatus itself, including detector imperfections, loss in optical fibers, and stray electromagnetic fields. These disturbances alter the quantum states representing information – typically photons – leading to bit errors and a reduction in signal fidelity. Consequently, the security of quantum key distribution (QKD) protocols is compromised as an eavesdropper can exploit the increased error rate to gain information without being detected, or an authorized party may be unable to establish a secure key. The severity of this impact is directly related to the noise level and its statistical properties.

Quantum noise, a significant impediment to practical quantum communication, presents itself in multiple statistical forms, most notably Gaussian and Poissonian noise. Gaussian noise affects quantum states by introducing fluctuations that follow a normal distribution, impacting both the amplitude and phase of signals and typically originating from thermal effects in detectors and transmission channels. Poissonian noise, conversely, arises from the discrete nature of photon detection, resulting in fluctuations in the number of detected photons; its variance is equal to its mean, and it’s particularly relevant in low-light conditions. These noise types differentially degrade quantum states; Gaussian noise tends to produce continuous errors, while Poissonian noise introduces discrete errors, necessitating tailored error correction strategies and impacting the performance of quantum key distribution protocols like BB84.

Accurate characterization of quantum noise is fundamental to the development of robust quantum communication systems. Error correction protocols rely on precise noise models to effectively decode transmitted quantum states; without this knowledge, error rates will exceed acceptable thresholds. Similarly, key distribution protocols, such as Quantum Key Distribution (QKD), must account for noise to accurately estimate the Quantum Bit Error Rate (QBER) and ensure the security of the generated key; higher noise levels directly reduce the secure key rate and potentially compromise security proofs. The ability to differentiate between noise sources – such as detector imperfections, channel loss, and environmental disturbances – allows for targeted mitigation strategies and optimized protocol parameters, ultimately enhancing both the performance and security of quantum communication links.

The finite-regime entropy approximation of the secure key rate <span class="katex-eq" data-katex-display="false">R_{N}</span> demonstrates robustness to a 10% underestimation of <span class="katex-eq" data-katex-display="false">H(Z)</span> across varying block sizes <span class="katex-eq" data-katex-display="false">N</span>, highlighting its practical applicability despite imperfect channel knowledge. — The finite-regime entropy approximation of the secure key rate $R_{N}$ demonstrates robustness to a 10% underestimation of $H(Z)$ across varying block sizes $N$ , highlighting its practical applicability despite imperfect channel knowledge.

Modeling Complexity: Hybrid Channels and the Pursuit of Accurate Representation

Quantum communication channels encountered in practical scenarios seldom conform to purely discrete or continuous descriptions; instead, they typically exhibit characteristics of both. Discrete variables, such as photon polarization or qubit states, often coexist with continuous variables representing parameters like amplitude and phase noise, or environmental fluctuations. This integration results in what are termed Hybrid Quantum Channels, demanding modeling techniques capable of accurately representing the correlations between these differing variable types. Ignoring this hybrid nature and treating the channel as solely discrete or continuous introduces inaccuracies that can significantly degrade the performance of quantum communication protocols, particularly in terms of secure key rate estimation and overall communication fidelity.

Gaussian Mixture Models (GMMs) function as a probabilistic framework for characterizing hybrid quantum channels by representing their probability distributions as a weighted sum of Gaussian distributions. This approach is particularly effective because it allows for the modeling of both discrete and continuous variables within a unified statistical structure, and crucially, captures the correlations that exist between these components. Specifically, the parameters of each Gaussian – mean and covariance – define the characteristics of a particular channel component, while the weighting coefficients determine the relative contribution of each component to the overall channel behavior. The ability to accurately represent these correlations is essential for predicting the behavior of the channel and optimizing quantum communication protocols, as it moves beyond the limitations of treating discrete and continuous aspects in isolation.

Accurate modeling of hybrid quantum channels is critical for optimizing Quantum Key Distribution (QKD) protocols and maximizing secure communication rates. Research indicates that estimating differential entropy, a key parameter in QKD security analysis, can be effectively approximated using the formula $H(Z) \approx H_2(Z) + log_2(Reff)$ . This approximation maintains a differential entropy estimation error within the 10% threshold, a performance level deemed crucial for reliable secure key rate estimation in practical QKD systems. $H(Z)$ represents the differential entropy of the channel, $H_2(Z)$ denotes the differential entropy calculated assuming a simplified channel model, and $Reff$ is an effective noise parameter accounting for the discrepancy between the actual and simplified models.

Reaching Beyond Fiber: Satellite Links and the Promise of Global Quantum Networks

Current quantum communication methods, reliant on fiber optic cables, face inherent distance limitations due to signal loss. Satellite Quantum Key Distribution (QKD) and free-space optics present viable pathways to circumvent these constraints by leveraging the negligible attenuation of signals in the atmosphere and space. These technologies utilize photons transmitted through the air or to and from orbiting satellites to establish secure communication links across intercontinental distances. By shifting the communication channel away from the confines of optical fiber, these approaches theoretically enable the creation of a global quantum network, facilitating unconditionally secure communication between any two points on Earth. The practical realization of such a network demands overcoming challenges related to atmospheric turbulence, signal acquisition, and maintaining quantum states over vast distances, but the potential benefits for secure data transmission are substantial.

Effective long-distance quantum communication via satellite or free-space optics fundamentally depends on a precise understanding of the quantum channel itself. These “hybrid quantum channels” are not the perfect, noise-free pathways envisioned in theoretical models; rather, they present a complex interplay of atmospheric turbulence, signal attenuation, and background noise. Accurately characterizing these factors – including the precise distribution of photon loss and the correlation of noise – is crucial for building reliable quantum links. Sophisticated modeling and experimental techniques are employed to map these channel characteristics, allowing for the development of adaptive optics and error correction protocols that mitigate the impact of noise and ensure the secure transmission of quantum information. Without this detailed characterization, even the most advanced quantum key distribution protocols would be vulnerable to eavesdropping or simply fail to function over significant distances.

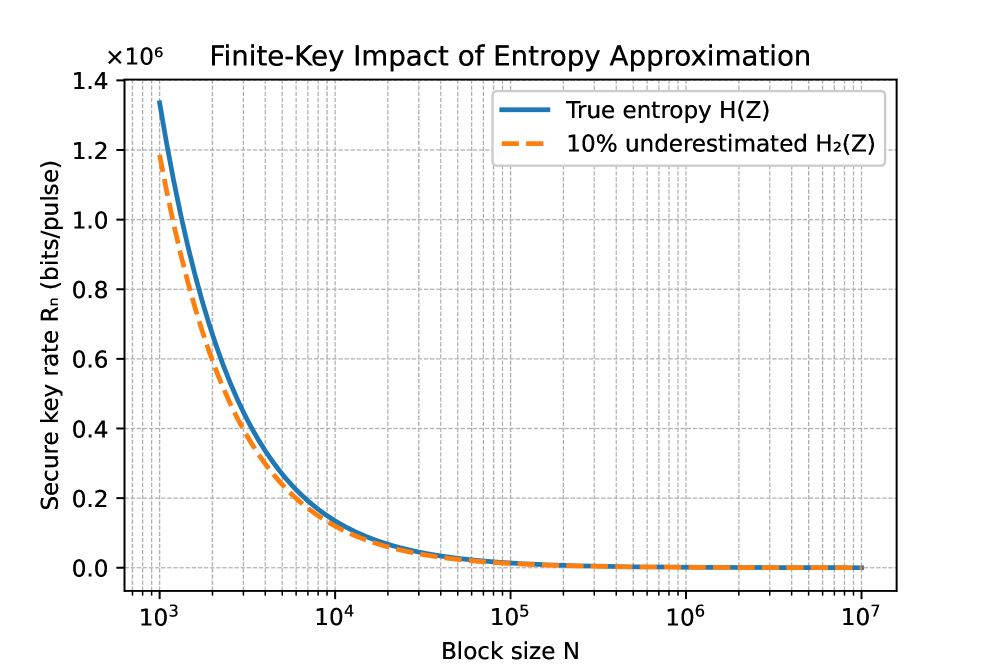
Achieving secure long-distance quantum communication demands accounting for real-world imperfections in transmission. Finite-Key Quantum Key Distribution (QKD) offers a crucial solution by enabling secure key generation even with limited data and imperfect devices. This approach doesn’t assume an infinite amount of data to achieve security, instead quantifying the potential for eavesdropping and setting correspondingly conservative key rates. Recent advancements have refined these calculations, achieving an approximation error of no more than 10% in estimating the secure key rate. This level of precision is particularly significant for finite-key QKD protocols, as it directly impacts the achievable key length and ensures robust security even when dealing with practical constraints and potential attacks – a critical step toward building truly secure global quantum networks.

Refining the Signal: Reverse Reconciliation and the Pursuit of Optimal Key Distribution

Quantum Key Distribution (QKD) relies on the principles of quantum mechanics to guarantee secure communication, but real-world implementations are susceptible to noise and imperfections. Reverse Reconciliation emerges as a crucial error correction technique to combat these issues, significantly boosting the performance of QKD systems. Unlike traditional methods that focus on identifying and correcting errors, Reverse Reconciliation strategically discards a portion of the raw key to enhance the reliability of the remaining bits. This approach, while seemingly counterintuitive, effectively reduces the error rate and increases the secure key rate achievable between communicating parties. By intelligently managing information loss, Reverse Reconciliation enables QKD protocols to function more effectively in noisy environments, paving the way for more practical and robust quantum communication networks.

The performance of Reverse Reconciliation, a crucial error correction method in Quantum Key Distribution, is fundamentally linked to the $Reff$ parameter, known as the Effective Noise Rank. This value doesn’t simply quantify the amount of noise, but rather its complexity – how many independent noise modes are present. A lower $Reff$ indicates simpler, more predictable noise that Reverse Reconciliation can efficiently correct, leading to higher key rates and improved security. Conversely, as noise becomes more complex – increasing $Reff$ – the reconciliation process demands greater resources and becomes less effective. Understanding and minimizing $Reff$ is therefore paramount for building practical quantum communication systems, as it directly impacts the achievable distance and security of key distribution, allowing for optimized protocols tailored to the specific noise characteristics of a given quantum channel.

The development of genuinely secure and functional quantum communication networks hinges on continued advancements in both noise reduction and reconciliation techniques. Current research indicates a promising path forward, leveraging the approximation $H(Z) \approx H_2(Z) + log_2(Reff)$ , where $H(Z)$ represents differential entropy, $H_2(Z)$ is the binary entropy, and $Reff$ denotes the Effective Noise Rank. This approximation proves increasingly accurate as noise complexity, quantified by $Reff$ , grows, offering a robust method for estimating information leakage during key distribution. Consequently, protocols can be optimized to maximize secure key rates even in noisy environments, ultimately bringing the promise of unconditionally secure communication closer to reality. Future investigations prioritizing minimization of noise and refinement of reconciliation strategies will be instrumental in realizing the full potential of quantum key distribution and establishing practical, widespread quantum networks.

The research meticulously constructs a unified framework for understanding hybrid quantum noise, revealing an equivalence between collision and differential entropy under defined conditions. This echoes a sentiment shared centuries ago by Isaac Newton: “If I have seen further it is by standing on the shoulders of giants.” The work doesn’t claim to solve quantum noise, but rather refines the tools for its analysis – building upon established entropy concepts to offer a more precise measurement. Predictive power, in this instance, isn’t causality – it’s a more accurate metric for evaluating the security and performance of next-generation quantum communication systems, a step towards verifiable, robust data transmission.

What Lies Ahead?

The demonstrated equivalence of collision and differential entropy, while holding under the stipulated Gaussian mixture model conditions, begs the question of its robustness. Future work must rigorously map the boundaries of this equivalence – specifically, the degree of deviation permissible in channel characteristics before the security advantages predicated on this framework erode. The current analysis, like most, relies on a mathematical description of noise; real-world channels rarely conform perfectly. Therefore, exploration of entropy estimators resilient to model mismatch represents a crucial next step.

Furthermore, the emphasis on Gaussian mixtures, while analytically tractable, may impose an artificial constraint. The utility of this unified framework will be truly tested by its application to more complex noise profiles – those exhibiting non-Gaussian characteristics or time-varying correlations. A fruitful avenue lies in adapting Rényi entropy, already hinted at in this work, to provide a more generalized measure, potentially revealing previously overlooked vulnerabilities or opportunities for optimization.

It remains an open question whether this refined entropy characterization translates directly into demonstrably superior key rates in practical Quantum Key Distribution systems. The correlation between mathematical elegance and real-world performance is, notoriously, weak. The pursuit of increasingly accurate models is not an end in itself; the ultimate metric remains the secure transmission of information, and that demands ongoing experimental validation.

Original article: https://arxiv.org/pdf/2602.00705.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/