Author: Denis Avetisyan
Researchers have developed a faster and more efficient method for calculating the half-lives of alpha-decaying nuclei, offering a valuable tool for nuclear physics and astrophysics.
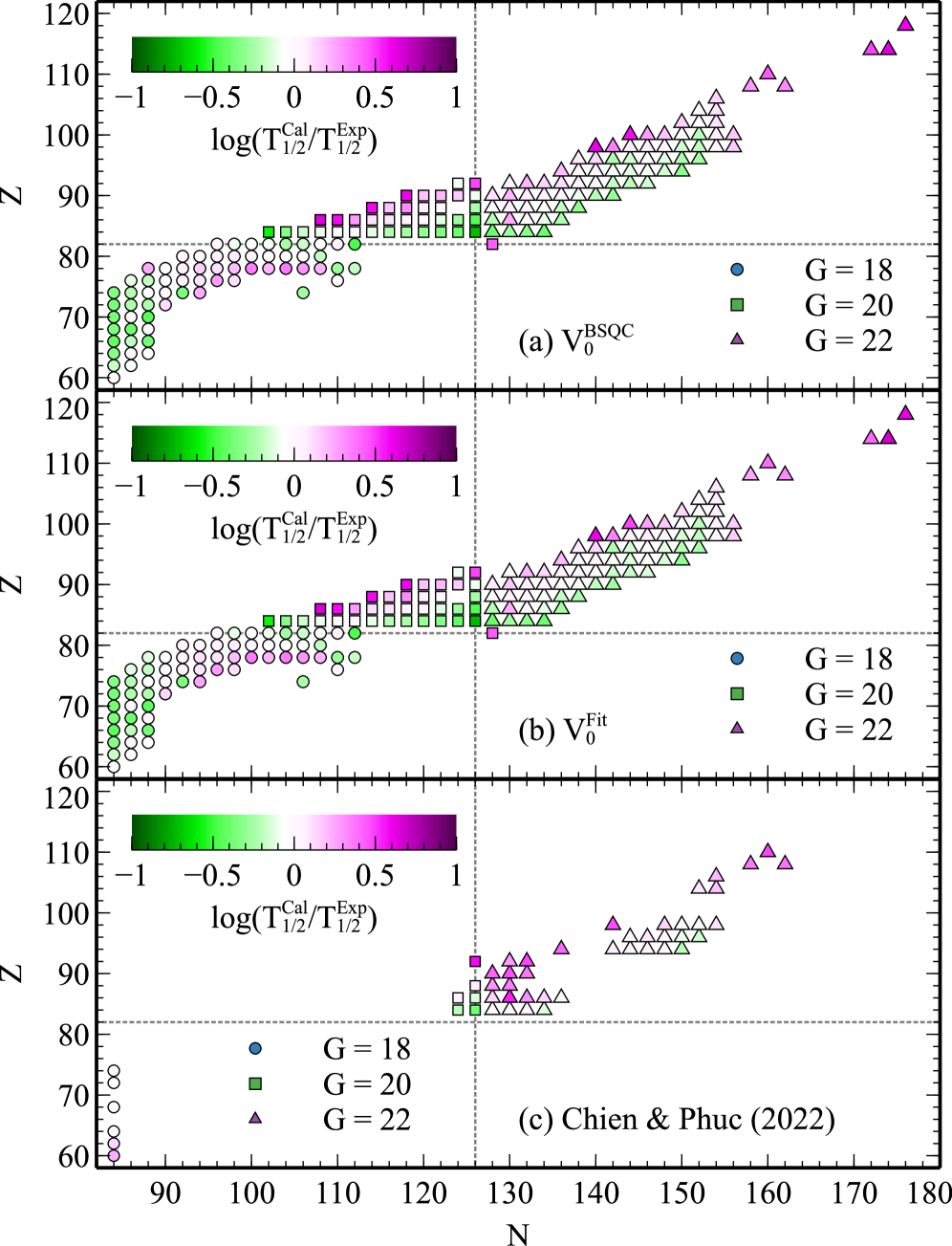
A global potential constrained by the Bohr-Sommerfeld quantization condition accurately models alpha decay half-lives for even-even nuclei using a semi-classical approach.
Predicting α-decay rates remains a challenge in nuclear physics, demanding both accuracy and computational efficiency. This work, ‘A global potential constrained by the Bohr-Sommerfeld quantization condition for α-decay half-lives of even-even nuclei’, presents a semi-classical framework employing a Woods-Saxon potential whose depth is rigorously determined by imposing the Bohr-Sommerfeld quantization condition. The resulting global parametrization successfully reproduces experimental half-lives with accuracy comparable to direct calculations, offering a computationally streamlined approach. Could this method be extended to predict decay pathways in superheavy nuclei, further refining our understanding of nuclear stability?
The Quantum Dance of Decay: A Fundamental Challenge
Alpha decay, a fundamental process in the realm of nuclear physics, offers an unparalleled glimpse into the bizarre rules governing the quantum world. While seemingly straightforward – the emission of an alpha particle from an unstable nucleus – a complete and accurate theoretical description has proven remarkably challenging. The difficulty stems from the need to reconcile quantum mechanics with the strong nuclear force, which dictates interactions within the nucleus. Current models must account for the probabilistic nature of quantum events, the complex potential energy landscape governing particle emission, and the inherent uncertainties in predicting decay rates. Despite decades of research, achieving a consistently precise theoretical framework remains a cornerstone challenge, pushing the boundaries of computational power and our understanding of the nuclear forces at play.
The phenomenon of alpha decay isn’t simply a matter of a nucleus ejecting a particle; it fundamentally involves a delicate interplay between the emitted alpha particle and the remaining daughter nucleus. This system isn’t isolated; rather, it’s governed by a potential energy landscape that dictates the probability of escape. Accurately modeling this potential is crucial, as it encapsulates the strong nuclear force, the electrostatic repulsion between the alpha particle and the daughter nucleus, and quantum mechanical effects like tunneling. The shape of this potential-often visualized as a barrier the alpha particle must overcome-directly influences the decay rate, making its precise description a central challenge in nuclear physics. Understanding how the alpha particle ‘feels’ this potential, and how that interaction evolves over time, is key to predicting and interpreting observed decay patterns.
Historically, calculating alpha decay rates has presented a significant challenge due to the conflicting demands of accuracy and computational cost. Early models, while conceptually sound, often relied on approximations to simplify the complex interactions within the nucleus, leading to discrepancies between theoretical predictions and experimental observations. More sophisticated methods, capable of capturing finer details of the nuclear potential, frequently require immense computational resources, making them impractical for predicting decay rates across a wide range of isotopes. This trade-off stems from the need to solve the time-independent Schrödinger equation for the alpha particle, a task complicated by the many-body nature of the nucleus and the diffuse nature of the potential barrier. Consequently, researchers continually seek innovative approaches – such as improved numerical techniques and refined theoretical frameworks – to bridge the gap between precision and efficiency in modeling this fundamental process.
Bridging Theory and Reality: A Semi-Classical Approach
The semi-classical description of alpha decay utilizes the Wentzel-Kramers-Brillouin (WKB) approximation to calculate the probability of alpha particle tunneling through the potential barrier created by the strong nuclear force and electrostatic repulsion. This approximation is valid when the potential varies slowly compared to the de Broglie wavelength of the alpha particle. The tunneling probability, T \approx \exp(-2\in t_{a}^{b} \sqrt{\frac{2m}{\hbar^2} (V(x) - E)} dx, where m is the alpha particle mass, \hbar is the reduced Planck constant, V(x) is the potential energy, and E is the alpha particle’s energy, dictates the decay rate. The integral is evaluated between the classical turning points a and b, defining the region where tunneling is possible. This method provides a quantitative estimate of alpha decay rates based on the shape and height of the potential barrier.
The semi-classical framework for alpha decay demands a rigorous definition of the nuclear potential to maintain physical consistency, achieved through the application of the Bohr-Sommerfeld quantization condition. This condition, derived from requiring the integral of the momentum over a complete period of motion to be an integer multiple of 2\pi\hbar, effectively discretizes the classically allowed energy levels within the potential. Specifically, it constrains the potential to allow only bound states and ensures that the wavefunction vanishes sufficiently rapidly at both spatial boundaries. Failure to satisfy the Bohr-Sommerfeld condition can lead to unphysical solutions, such as unbound states or wavefunctions that do not normalize correctly, thereby invalidating the calculated tunneling probability and alpha decay rate.
The predictive power of the semi-classical approach to alpha decay is fundamentally dependent on the chosen nuclear potential. While numerous potential models exist, the Woods-Saxon potential is frequently employed due to its realistic representation of the nuclear force and its mathematical tractability. This potential, defined as V(r) = -V_0 / (1 + exp((r-R)/a)), where V_0 is the potential depth, R the nuclear radius, and a the diffuseness parameter, provides a reasonable approximation of the nuclear interaction experienced by alpha particles attempting to tunnel through the potential barrier. The accuracy of calculated decay rates is therefore directly tied to the appropriate parameterization of these Woods-Saxon potential components, requiring careful consideration of nuclear structure data and empirical fits.
Balancing Precision and Efficiency: Potential Refinement
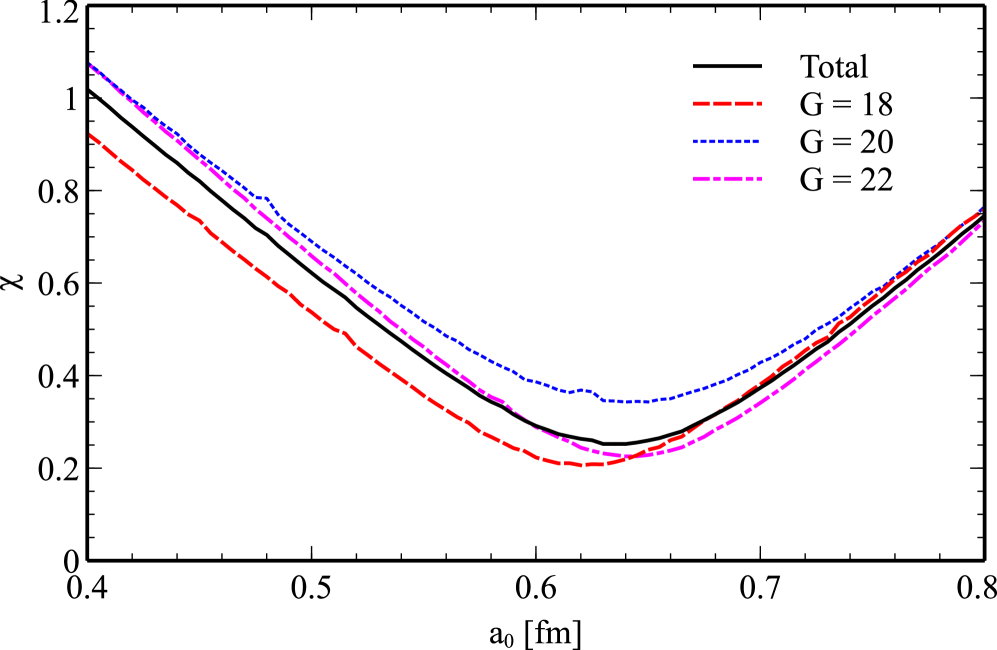
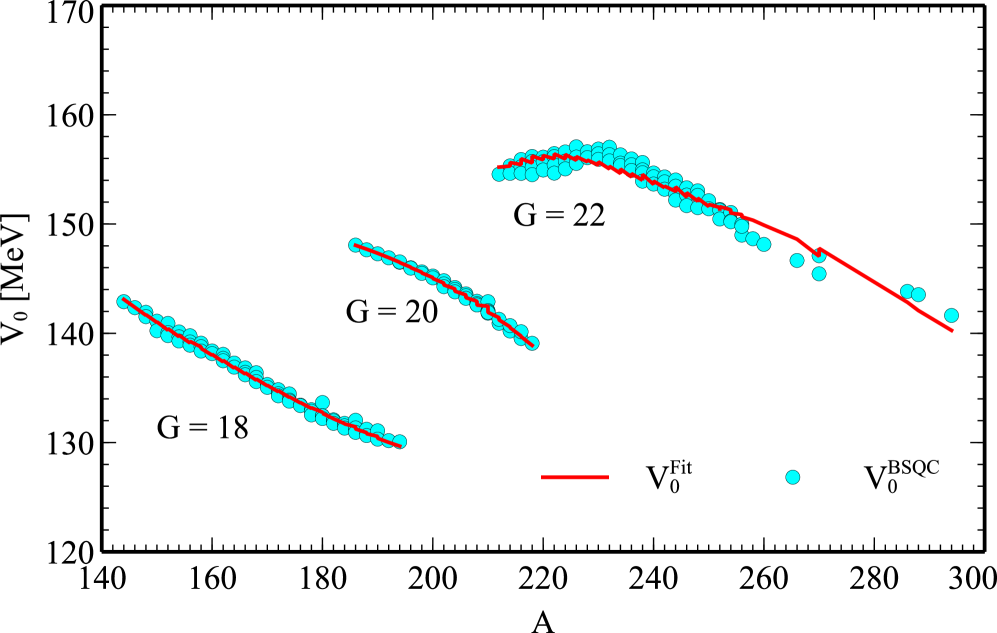
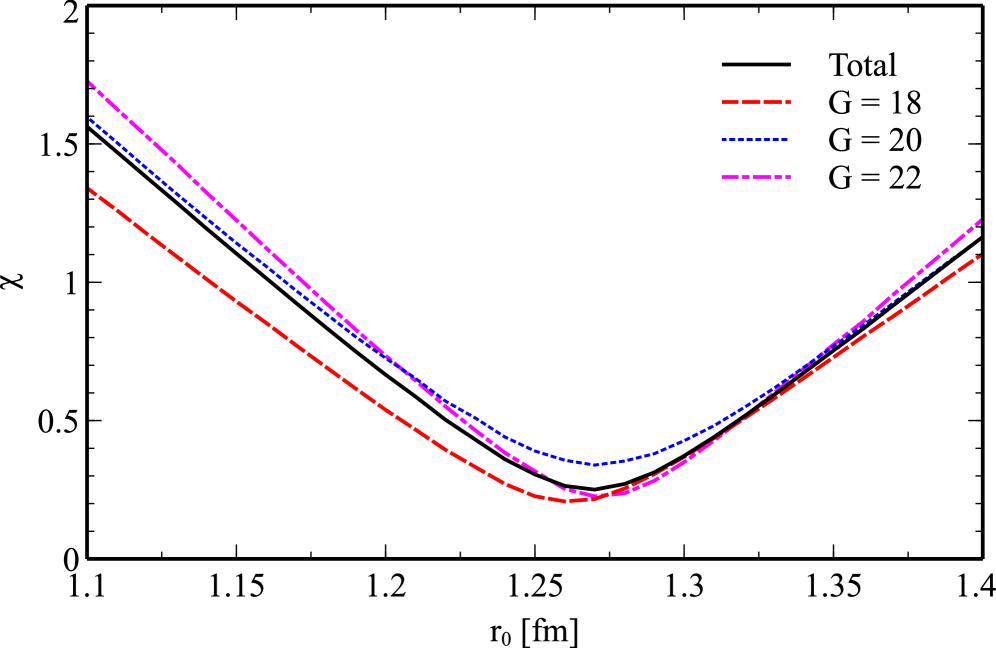
The potential depth, a critical parameter within the Woods-Saxon potential model, directly impacts the calculated decay rates of nuclei undergoing alpha emission. This parameter defines the strength of the nuclear potential barrier that an alpha particle must tunnel through to escape the nucleus; a deeper potential well corresponds to a lower decay probability, and vice versa. Therefore, accurate determination of the potential depth is essential for reliable predictions of alpha decay half-lives. Our calculations ensure consistency between the chosen potential depth and the Bohr-Sommerfeld condition, which relates the potential depth to the nuclear radius and the number of protons and neutrons, thereby maintaining the theoretical framework’s internal consistency and predictive power. Failure to adhere to this condition would introduce systematic errors in the calculated decay rates.
To reduce computational demands without compromising result fidelity, a fitted parametrization is utilized to approximate the potential depth within the Woods-Saxon potential. This approach circumvents the need for iterative calculations of the potential depth for each nucleus, significantly decreasing processing time. The parametrization is derived from a comprehensive analysis of known nuclear properties and ensures that the calculated potential depth remains consistent with experimental observations. This allows for rapid and accurate determination of nuclear decay rates across a wide range of nuclei, making large-scale calculations feasible.
The presented method exhibits a root-mean-square (RMS) deviation of 0.250 when comparing calculated half-lives to experimentally determined values for a dataset of 178 even-even nuclei. This RMS deviation serves as a quantitative measure of the method’s accuracy, indicating a strong correlation between theoretical predictions and empirical observations. The relatively low deviation confirms the method’s ability to reliably predict nuclear half-lives with a high degree of precision while maintaining computational efficiency, suggesting a balanced approach to both accuracy and processing time.
Echoes of Validation: Implications for Nuclear Structure
The reliability of any theoretical model rests on its ability to reproduce observed phenomena, and in the realm of nuclear physics, this is often achieved by comparing calculated half-lives – the time it takes for half of a radioactive sample to decay – with experimentally determined values. This comparison isn’t simply a matter of matching numbers; a quantitative metric is needed to assess the overall agreement. The research utilizes the Root Mean Square (RMS) deviation as this metric, effectively measuring the average difference between the calculated and experimental half-lives. A lower RMS deviation indicates a stronger correlation and, therefore, a more accurate model; it provides a single, concise figure to encapsulate the model’s predictive power and allows for direct comparison with other theoretical approaches. This rigorous validation process is crucial for establishing the model’s credibility and its potential to accurately describe and predict the behavior of atomic nuclei.
The accuracy of nuclear models often relies on bridging the gap between macroscopic and microscopic descriptions of the nucleus. While liquid-drop models provide a good starting point by treating the nucleus as a fluid, they inherently lack the detail to capture quantum mechanical effects like shell structure. Incorporating shell correction energy into these models represents a significant advancement, as it accounts for the discrete energy levels arising from the nucleus’s quantum nature. This correction term effectively refines the predicted nuclear properties by moving beyond a purely classical picture, and acknowledging the influence of nucleon arrangement within defined quantum states. By including these quantum effects, the model’s fidelity is greatly enhanced, enabling more accurate predictions of phenomena such as nuclear decay rates and stability.
The developed semi-classical model demonstrates a strong capacity for predicting nuclear half-lives, achieving a root-mean-square (RMS) deviation of just 0.250 when compared to experimental data. This level of accuracy is particularly noteworthy as it aligns closely with results obtained through more computationally intensive methods; a directly calculated Blocked Schrödinger Quadratic (BSQC) potential yields an RMS deviation of 0.253, while a semi-microscopic Double-Folding potential achieves 0.259. The consistency across these diverse approaches effectively validates the model’s effectiveness, suggesting it provides a reliable and efficient means of approximating nuclear decay rates without sacrificing predictive power. This positions the model as a valuable tool for exploring nuclear structure and informing future research in the field.
The pursuit of computational efficiency, as demonstrated in this study of alpha decay half-lives, echoes a fundamental principle of enduring systems. One might consider that every iteration of the Woods-Saxon potential, every refinement of the Bohr-Sommerfeld quantization condition, represents a commitment against entropy. As Jean-Paul Sartre observed, “Man is condemned to be free.” This freedom, within the framework of nuclear physics, manifests as the choice of approximation-balancing accuracy with computational cost. Delaying more precise, but demanding, calculations is a tax on ambition, much like accepting a less graceful decay of a system’s initial promise. The paper acknowledges this trade-off, aiming for a method that ages gracefully, retaining essential fidelity while minimizing resource expenditure.
The Unfolding Chronicle
The presented method, while computationally expedient, merely refines an existing lineage. The Bohr-Sommerfeld condition, a historically significant attempt to bridge classical and quantum realms, continues to yield approximations. Each successful calculation is not an arrival, but a logged point on the timeline of our incomplete understanding. The Woods-Saxon potential, a pragmatic choice, remains a phenomenological construct-a useful fiction. Future iterations will inevitably confront the inherent limitations of treating nuclei as purely classical systems bound by potentials.
The true challenge lies not in faster computation, but in a deeper ontological shift. Can a semi-classical model, however refined, truly capture the essence of alpha decay? Or does the process necessitate a fully quantum mechanical treatment, acknowledging the probabilistic nature of barrier penetration beyond the scope of WKB approximations? The half-life, ultimately, is not a fixed duration, but a measure of the system’s resistance to inevitable entropy.
Deployment of this technique is a moment on that timeline-a useful tool for predicting decay rates. Yet, the most intriguing questions remain untouched. The system’s chronicle will continue, accumulating data, refining models, and revealing, perhaps, the delicate balance between order and decay that governs the nucleus-and, by extension, all things.
Original article: https://arxiv.org/pdf/2602.02070.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- Gold Rate Forecast
- How to Unlock the Mines in Cookie Run: Kingdom
- How to Find & Evolve Cleffa in Pokemon Legends Z-A
- Most Underrated Loot Spots On Dam Battlegrounds In ARC Raiders
- Gears of War: E-Day Returning Weapon Wish List
- The Saddest Deaths In Demon Slayer
- FromSoftware’s Duskbloods: The Bloodborne Sequel We Never Knew We Needed
- Bitcoin Frenzy: The Presales That Will Make You Richer Than Your Ex’s New Partner! 💸
- Bitcoin’s Big Oopsie: Is It Time to Panic Sell? 🚨💸
- All Pistols in Battlefield 6
2026-02-03 16:24