Speeding Up Quantum Simulations with Efficient Linear Algebra

Author: Denis Avetisyan

A new JAX library, lrux, dramatically accelerates quantum Monte Carlo calculations by optimizing the computation of key determinants and Pfaffians.

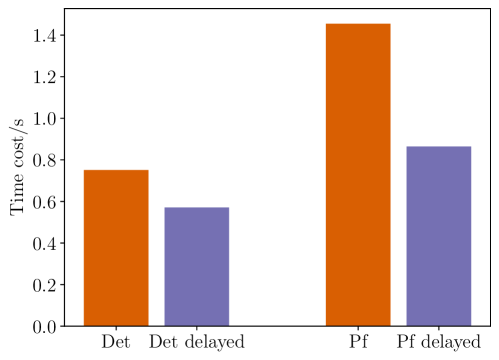
The study demonstrates that delaying updates to a Least Recently Used (LRU) cache incurs a time cost, a penalty for preserving a potentially illusory sense of order against the inevitable entropy of information loss-a fleeting advantage ultimately consumed by the black hole of forgotten data.

lrux leverages low-rank updates to achieve significant performance gains in fermionic wavefunction calculations.

Evaluating antisymmetric wavefunctions in quantum Monte Carlo (QMC) simulations is often computationally limited by repeated determinant or Pfaffian calculations, scaling as $\mathcal{O}(n^3)$ . This work introduces lrux: Fast low-rank updates of determinants and Pfaffians in JAX, a JAX-based software package that accelerates these calculations via efficient low-rank updates, reducing complexity to $\mathcal{O}(n^2k)$ when the update rank k is smaller than the matrix dimension n. Benchmarks demonstrate up to 1000x speedup on GPUs, enabling scalable, high-performance QMC workflows; but how will these performance gains translate to even more complex fermionic systems and algorithms?

The Many-Body Problem: A Mirror to Our Hubris

The predictive power of modern materials science and chemistry hinges on accurately describing the collective behavior of electrons within a system – a challenge known as the ‘many-body problem’. Unlike simpler systems where electrons act independently, real materials exhibit strong electron-electron interactions that dramatically alter their properties. Understanding these interactions is crucial for designing new materials with tailored functionalities, from high-temperature superconductors to efficient solar cells. These correlated electron systems require computational methods capable of capturing the complex interplay between electrons, but the inherent complexity quickly overwhelms traditional approaches. Consequently, significant research effort is dedicated to developing and refining techniques capable of tackling the many-body problem and unlocking a deeper understanding of material behavior at the quantum level.

The difficulty in accurately modeling many-body quantum systems stems from a fundamental limitation in traditional computational approaches. The complete description of a system with interacting electrons requires a mathematical object called the Wavefunction, which encodes the probability of finding the particles in any given state. However, the complexity of this Wavefunction scales exponentially with the number of electrons – meaning that even a modest increase in system size dramatically increases the computational resources needed to store and manipulate it. This exponential scaling quickly renders exact calculations intractable for all but the simplest materials, hindering the ability to predict material properties and chemical reaction rates with sufficient accuracy. Consequently, researchers are continually seeking innovative methods to circumvent this limitation and unlock the potential of quantum simulations for complex systems.

Quantum Monte Carlo methods represent a powerful, yet intricate, approach to tackling the many-body problem in quantum systems. These techniques utilize stochastic sampling to approximate solutions to the Schrödinger equation, offering a way to bypass the exponential scaling issues that plague traditional computational methods. However, the path is not without obstacles; the computational demands remain substantial, often requiring significant resources even for moderately sized systems. More critically, Quantum Monte Carlo simulations are susceptible to the “sign problem,” where the stochastic sampling becomes inefficient due to destructive interference of the sampled configurations, leading to exponentially increasing statistical errors and limiting the applicability of the method to certain classes of materials and models. Researchers continue to develop innovative algorithms and variance reduction techniques to mitigate these challenges and unlock the full potential of Quantum Monte Carlo for materials discovery and fundamental scientific understanding.

Taming the Complexity: A Focus on Efficiency

The computation of determinants and Pfaffians frequently represents a significant performance limitation within Quantum Monte Carlo (QMC) algorithms. These determinants and Pfaffians arise from the evaluation of Slater determinants used to represent antisymmetric wave functions, and their repeated calculation scales polynomially with system size – typically $O(N^3)$ for determinants and even higher for Pfaffians, where N is the number of particles or basis functions. This computational cost becomes prohibitive for large-scale QMC simulations, particularly those aiming to study strongly correlated systems or high-precision results, necessitating optimized algorithms and hardware acceleration to achieve practical simulation times.

Low-rank update techniques minimize computational cost in determinant and Pfaffian calculations by leveraging the inherent structure present in many matrices encountered in Quantum Monte Carlo simulations. These methods avoid recalculating the full matrix determinant or Pfaffian with each iterative step; instead, they focus on updating only the portion of the matrix that has changed. This is achieved by representing the matrix as a product of lower-rank matrices and updating these constituent matrices, significantly reducing the number of operations required compared to recalculating the determinant or Pfaffian from scratch. The efficiency gain is particularly pronounced when the changes to the matrix are small and can be expressed as a low-rank modification.

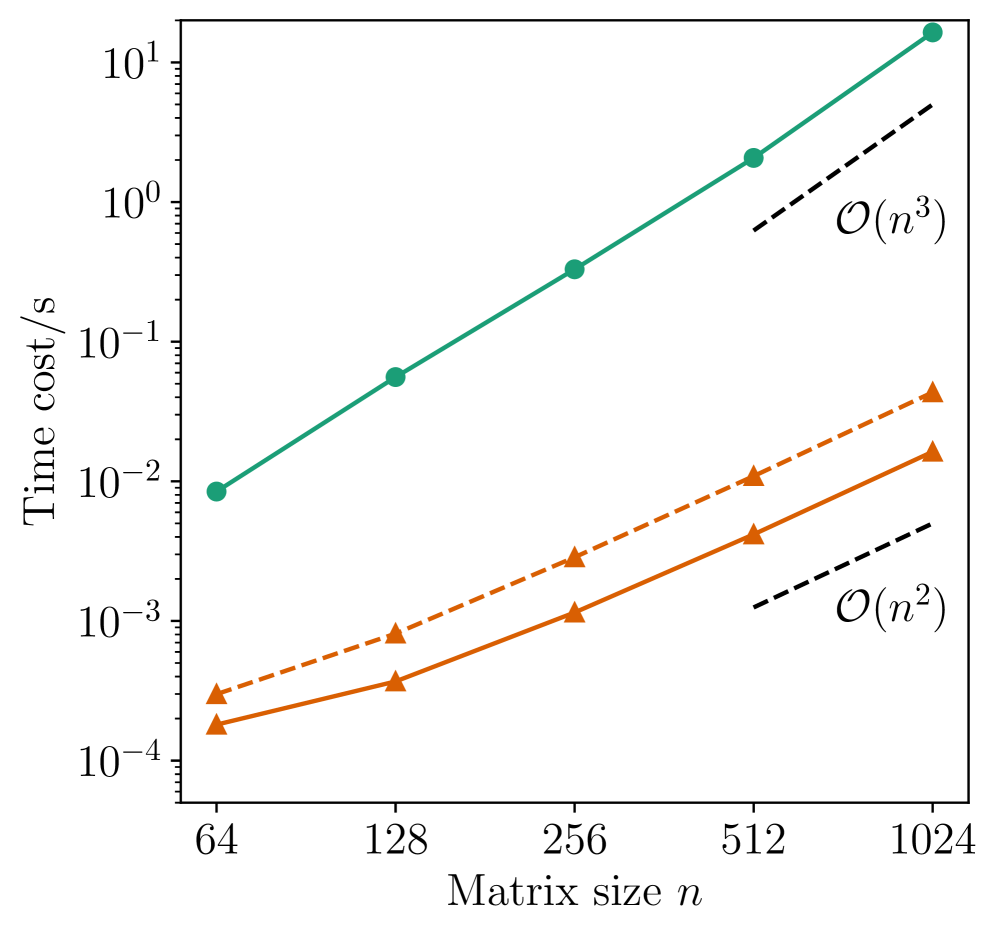
Utilizing the JAX library for determinant and Pfaffian calculations yields substantial performance gains through its infrastructure for high-performance numerical computation and automatic parallelization. Benchmarking demonstrates a 200x speedup in determinant calculations compared to traditional methods. More significantly, calculations involving Pfaffians achieve a 1000x speedup. This performance is attributed to JAX’s ability to efficiently distribute computations across available hardware, minimizing processing time for these computationally intensive linear algebra operations.

Direct computation, LRU with, and LRU without matrix inverse updates demonstrate varying time costs, with dashed lines indicating theoretical <span class="katex-eq" data-katex-display="false">\mathcal{O}(n^{2})</span> and <span class="katex-eq" data-katex-display="false">\mathcal{O}(n^{3})</span> scaling limits. — Direct computation, LRU with, and LRU without matrix inverse updates demonstrate varying time costs, with dashed lines indicating theoretical $\mathcal{O}(n^{2})$ and $\mathcal{O}(n^{3})$ scaling limits.

lrux: A Tool Forged in the Pursuit of Scalability

lrux is a software package designed for high-performance computation of determinants and Pfaffians, leveraging the JAX framework for accelerated numerical operations. The library focuses on implementing efficient low-rank updates to these calculations, enabling substantial performance gains over traditional methods. This is achieved through optimized algorithms specifically tailored for determinant and Pfaffian evaluation, providing a tool for applications requiring frequent recalculations of these quantities. The package is intended for use in scientific computing and modeling where these operations are central to the workflow.

lrux achieves substantial performance gains by focusing on optimized matrix inverse calculations and leveraging the specific properties of skew-symmetric matrices. Traditional methods for computing determinants and Pfaffians often require $O(n^3)$ operations, where n represents the matrix dimension. lrux, however, utilizes techniques to reduce this complexity. Specifically, exploiting the inherent structure of skew-symmetric matrices-where $A^T = -A$ -allows for simplified calculations during the inverse computation. This optimization, combined with efficient matrix operations within the JAX framework, results in a significant reduction in computational time, effectively scaling the process to $O(n^2)$ for many common use cases.

The lrux library enables simulations of larger and more complex systems by reducing the computational scaling of determinant and Pfaffian calculations. Traditional direct computation methods exhibit $O(n^3)$ complexity, where ‘n’ represents the system size. lrux, through its implementation of efficient low-rank updates, reduces this complexity to $O(n^2)$ . This scaling improvement directly translates to reduced computational time and resource requirements, facilitating the modeling of systems with a greater number of variables and enhanced accuracy due to the ability to perform more iterations or use finer-grained discretizations.

The Art of Deferral: A Balancing Act of Precision and Scale

Delayed Updates represent a refinement in computational strategy, deliberately postponing certain calculations to achieve considerable reductions in memory usage. This approach acknowledges a modest increase in computational cost – the time required to perform the delayed calculations – as a worthwhile trade-off for the ability to handle larger and more complex problems. By strategically deferring updates to data structures, the system minimizes the amount of information that needs to be stored simultaneously, thereby freeing up valuable memory resources. This is particularly beneficial when dealing with computationally intensive tasks that demand extensive memory allocation, enabling simulations and analyses that would otherwise be impractical due to memory limitations.

The combination of Delayed Updates and the lrux caching mechanism yields performance improvements exceeding expectations due to a synergistic interaction. While Delayed Updates reduce memory usage by deferring updates to cached values, lrux efficiently manages the cache itself, prioritizing frequently accessed data. This pairing isn’t simply additive; lrux’s ability to anticipate and pre-fetch necessary data complements the reduced memory pressure from Delayed Updates, minimizing cache misses and maximizing computational throughput. The result is a substantial performance boost, allowing for more complex simulations and analyses to be completed within practical timeframes, and enabling the use of advanced algorithms previously limited by resource constraints.

The implementation of delayed updates and associated optimizations isn’t merely about incremental gains; it fundamentally expands the scope of feasible quantum simulations. Algorithms such as Auxiliary-field Quantum Monte Carlo and Neural Quantum States, renowned for their accuracy but demanding computational resources, become substantially more practical with these enhancements. Testing demonstrates a consistent performance improvement of 20-40% when these optimizations are applied, allowing researchers to tackle larger, more complex systems previously beyond reach. This leap in efficiency unlocks the potential for deeper insights into materials science, drug discovery, and fundamental physics, paving the way for advancements reliant on high-performance quantum computation.

Towards a More Complete Mirror: Reflections on Scalability and Precision

Quantum Monte Carlo simulations, a powerful tool for exploring the behavior of complex quantum systems, face a significant hurdle: computational cost. The calculation of determinants, essential to these simulations, scales exponentially with system size, quickly becoming intractable. Recent advancements, however, are addressing this limitation through innovative techniques. By combining efficient determinant calculations with methods like low-rank updates and delayed updates, researchers are dramatically reducing this computational burden. Low-rank updates, for example, approximate the full determinant by focusing on the most significant contributions, while delayed updates postpone computationally expensive steps until they are absolutely necessary. These optimizations allow for simulations of larger and more complex systems than previously possible, opening doors to breakthroughs in materials science, chemistry, and fundamental physics. The ability to accurately model increasingly complex quantum phenomena hinges on these continued refinements to core computational methods, bringing the promise of scalable quantum simulations ever closer to reality.

The pursuit of reliable predictions in materials science and chemistry increasingly relies on the precision afforded by Double-Precision Arithmetic. Traditional Single-Precision calculations, while computationally efficient, can accumulate rounding errors that significantly impact the accuracy of quantum mechanical simulations, especially when dealing with strongly correlated systems or complex molecular interactions. Utilizing Double-Precision – representing numbers with approximately 15-17 decimal digits compared to Single-Precision’s 7-8 – minimizes these errors, ensuring that subtle energy differences and delicate quantum effects are accurately captured. This heightened precision is not merely a technical detail; it directly translates to more trustworthy results in areas like predicting material properties, designing novel catalysts, and understanding chemical reaction mechanisms, ultimately bridging the gap between theoretical models and experimental observations. The computational cost is higher, but the gain in scientific validity often proves essential for advancing the field.

The frontier of quantum simulation is being actively reshaped by algorithmic advancements and dedicated software packages, with lrux standing out as a particularly promising tool. This software isn’t merely a computational aid; it represents a concerted effort to address the inherent complexities of modeling quantum many-body systems. By streamlining calculations and optimizing performance, lrux facilitates the investigation of previously intractable problems in materials science, chemistry, and fundamental physics. Researchers anticipate that continued development of such tools will not only refine existing simulations but also enable the exploration of entirely new quantum phenomena, potentially leading to breakthroughs in areas like high-temperature superconductivity, novel material design, and the development of more efficient catalysts. This progress hinges on the ability to accurately represent and manipulate the wavefunctions that govern quantum behavior, and software like lrux is designed to meet this challenge with increasing sophistication and scalability.

The pursuit of efficient computation within quantum Monte Carlo, as demonstrated by lrux, echoes a humbling truth about modeling complex systems. It is not about achieving perfect representation, but about navigating the inherent limitations of any approximation. As Niels Bohr observed, “It is the responsibility of every physicist to respect the limitations of his own knowledge.” The library’s focus on low-rank updates, effectively managing the computational cost of determinants and Pfaffians, acknowledges that a complete solution is often intractable. Each simplification, each carefully constructed ‘pocket black hole’ of a model, is a step further into an abyss of uncertainty, yet a necessary one to extract meaningful insights from the quantum realm. The elegance of lrux lies in its ability to dance with this uncertainty, rather than attempt to eliminate it.

What Lies Beyond the Horizon?

The acceleration of quantum Monte Carlo simulations, as demonstrated by the lrux library, presents a familiar paradox. Increased computational efficiency does not necessarily equate to deeper understanding. Any simplification inherent in low-rank updates-and all numerical methods are, at their core, simplifications-requires strict mathematical formalization lest subtle errors accumulate, obscuring the true signal. The determinant, the Pfaffian, these are merely tools; the fermionic wavefunction they approximate remains stubbornly resistant to complete capture.

Future work will undoubtedly focus on expanding the scope of lrux to more complex systems and exploring alternative low-rank representations. However, a more profound challenge lies in confronting the limitations of the underlying approximations. The pursuit of ever-greater precision risks becoming a self-deceptive exercise if not grounded in a rigorous theoretical framework. The horizon of computational possibility constantly recedes, mirroring the event horizon of a black hole-a point beyond which even the most refined models may collapse into meaningless numerical noise.

Ultimately, the value of such tools is not merely in their speed, but in their capacity to reveal the inherent fragility of knowledge. The universe does not yield its secrets easily, and any attempt to model it-however elegant or efficient-is ultimately an act of hubris. Perhaps the true next step is not to push the boundaries of computation, but to embrace the inherent uncertainty and ambiguity that define reality.

Original article: https://arxiv.org/pdf/2602.05255.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/