Author: Denis Avetisyan
New research reveals how accurately modeling the behavior of extremely dense quark matter requires careful consideration of medium effects and a consistent regularization scheme.
This review explores violations of the conformal limit at finite density, utilizing effective models and lattice QCD to understand the equation of state and speed of sound in dense baryonic matter.
The expectation of conformal symmetry at high density in quantum chromodynamics (QCD) is increasingly challenged by observations of its breakdown in realistic scenarios. This work, ‘Violation of the Conformal Limit at Finite Density: Insights from Effective Models and Lattice QCD’, investigates these violations through a comparative analysis of effective models-regularized via a medium separation scheme-and lattice QCD simulations. Our findings demonstrate that a consistent treatment of medium effects is crucial for accurately describing the equation of state and, specifically, the speed of sound in dense quark matter. Can this approach provide a pathway towards a more complete understanding of the QCD phase diagram and the emergence of novel phases at extreme densities?
Unveiling the Extremes: Probing Ultra-Dense Matter
The realm of ultra-dense matter, exemplified by the cores of neutron stars, poses a formidable challenge to contemporary nuclear physics. These celestial objects pack immense mass into incredibly small volumes, creating conditions where the very fabric of matter is pushed to its limits. At such extreme densities, the familiar building blocks of atomic nuclei-protons and neutrons-are crushed, and their constituent quarks may become deconfined, resulting in exotic states of matter. Studying this behavior isn’t simply an academic exercise; it demands a reevaluation of fundamental theories governing the strong nuclear force and the nature of matter itself. Existing theoretical tools, reliant on approximations that work well at lower densities, break down under these conditions, necessitating the development of entirely new approaches to accurately model and predict the properties of matter at the threshold of gravitational collapse.
At extreme densities, such as those found within neutron stars, the fundamental theory of strong interactions – Quantum Chromodynamics, or QCD – encounters a critical limitation. Conventional perturbative methods, which rely on approximating solutions based on small deviations from a simple starting point, break down entirely. This failure arises because the strong force, governing interactions between quarks and gluons, becomes overwhelmingly dominant at high densities. Instead of being a small correction, the interaction strength becomes comparable to, or even larger than, the energy scales involved, rendering the perturbative expansion meaningless and unreliable. Consequently, predicting the behavior of matter under these conditions requires fundamentally different theoretical tools, moving beyond the reach of standard QCD calculations.
At extreme densities, such as those found within neutron stars, matter transitions into states where traditional calculations based on perturbative Quantum Chromodynamics become unreliable due to the overwhelming strength of interactions. Consequently, effective field theories emerge as indispensable tools for investigating dense quark matter. These theories intentionally simplify the complex underlying physics, focusing on the relevant degrees of freedom at a given energy scale and encapsulating the effects of unknown high-energy phenomena within a limited set of parameters. By systematically incorporating these parameters, physicists can construct models that accurately describe the properties of dense quark matter – including its equation of state, transport coefficients, and collective behavior – and ultimately shed light on the fundamental nature of matter under the most extreme conditions in the universe. This approach doesn’t claim to be a complete description, but rather a controlled approximation allowing for meaningful predictions and comparisons with observational data.
A Non-Perturbative Framework: The NJL Model
The Nambu-Jona-Lasinio (NJL) model provides a non-perturbative approach to investigating quark and diquark dynamics in dense matter by representing the fundamental interactions through four-fermion couplings. This simplification allows for the treatment of strong interactions beyond the limitations of perturbative quantum chromodynamics (QCD), particularly at high densities where perturbative methods fail. The model describes quarks as effectively massive particles arising from spontaneous chiral symmetry breaking, and incorporates diquark interactions to account for color superconductivity potentially present in dense quark matter. While not a direct solution to QCD, the NJL model serves as a valuable tool for exploring the equation of state, phase transitions, and collective properties of matter under extreme conditions, offering both analytical accessibility and the capacity for numerical simulations.
Spontaneous chiral symmetry breaking within the NJL model manifests through the generation of a quark condensate, \langle \overline{q}q \rangle, in the vacuum state. This condensate represents the formation of quark-antiquark pairs, lowering the energy of the system despite the absence of explicit chiral symmetry breaking terms in the Lagrangian. The magnitude of the quark condensate serves as an order parameter for this symmetry breaking; a non-zero value indicates that chiral symmetry is broken and the quarks acquire an effective mass. This dynamical generation of quark mass is a crucial aspect of the model and influences the properties of hadrons and the behavior of dense quark matter, as it effectively modifies the single-particle spectrum of quarks.
The Nambu-Jona-Lasinio (NJL) model functions as an effective field theory derived from Quantum Chromodynamics (QCD) by focusing on the low-energy degrees of freedom – quarks and diquarks – and omitting explicit gluon fields. This simplification enables analytical calculations, such as the derivation of gap equations to determine the dynamically generated quark mass, which would be intractable in full QCD. Furthermore, the model’s Lagrangian allows for systematic numerical studies via methods like mean-field approximations and functional renormalization group techniques, providing insights into the equation of state, phase diagrams, and collective properties of dense quark matter, including color superconductivity and chiral phase transitions, without requiring direct lattice QCD simulations at finite density.
Taming the Infinities: Regularization Strategies
Quantum field theory (QFT) calculations, while theoretically sound, frequently produce infinite results due to the integration over all possible momentum states, including arbitrarily high energies and frequencies. These infinities arise from divergences in loop integrals, inherent in perturbative calculations involving virtual particle exchanges. To obtain finite, physically meaningful predictions, regularization techniques are employed. These techniques modify the theory at high energies-introducing a cutoff, adding auxiliary fields, or modifying the integration contour-to render the integrals finite. The regularization scheme serves as a mathematical procedure; the physically observable quantities must remain unchanged after removing the regulator in a process called renormalization, ensuring the predictions are independent of the specific regularization method chosen. \in t_0^\in fty dk \, k^n diverges for n \ge -1 , illustrating the need for regularization.
The Nambu-Jona-Lasinio (NJL) model, when subjected to calculations, frequently produces divergent integrals necessitating the implementation of regularization techniques. Common approaches include the three-dimensional cutoff, which introduces a momentum-space upper limit Λ to effectively dampen high-momentum contributions; Pauli-Villars regularization, employing fictitious massive bosons to cancel infinities arising from massless fermions; and the medium separation scheme. Each method addresses ultraviolet divergences by modifying the integration process, ultimately yielding finite and physically meaningful results for quantities calculated within the NJL framework, such as particle masses and scattering amplitudes. The choice of regularization scheme can impact the precise values obtained, but should not alter the underlying physics of the model.
The medium separation scheme provides a method for calculating properties of dense matter by explicitly distinguishing between contributions originating from the medium itself and those from the vacuum. This is achieved through a specific momentum routing procedure within loop integrals, assigning momenta to fermion lines based on whether they represent particles in the medium or in the vacuum. By consistently separating these contributions, the scheme avoids artificial violations of the conformal limit which can arise in other regularization methods when dealing with strong interactions. This approach allows for a more accurate determination of medium-dependent effects, such as changes to particle properties or the equation of state, in environments like neutron stars or heavy-ion collisions.

Echoes of Compression: Speed of Sound and the Equation of State
The behavior of sound waves traveling through extremely dense matter provides a unique window into its fundamental properties. Specifically, the speed at which sound propagates is acutely sensitive to the equation of state – a description of how pressure relates to density – thereby revealing details about the matter’s compressibility and the interactions between its constituent particles. A stiffer equation of state, indicating greater resistance to compression, translates to a higher speed of sound, while softer matter allows sound to travel more slowly. By meticulously measuring or modeling this speed across a range of densities and temperatures, physicists can map out the equation of state and gain crucial insights into the exotic forms of matter expected to exist within neutron stars and during heavy-ion collisions; this approach offers a powerful, indirect method for probing matter under conditions impossible to replicate terrestrially.
Investigations utilizing the Nambu-Jona-Lasinio (NJL) model reveal that the behavior of dense matter deviates from the theoretically predicted conformal limit at lower densities. These calculations incorporate both isospin density – the imbalance between up and down quarks – and quark chemical potential, a measure of the external influence driving particle creation. The model predicts that as density increases, certain interactions become significant, causing a departure from the idealized conformal behavior where the equation of state is scale-invariant. This deviation is crucial, as it suggests that the internal structure and interactions within dense matter are more complex than previously assumed, and provides a pathway to understand the nuanced relationship between density, particle composition, and the overall equation of state governing this exotic form of matter.
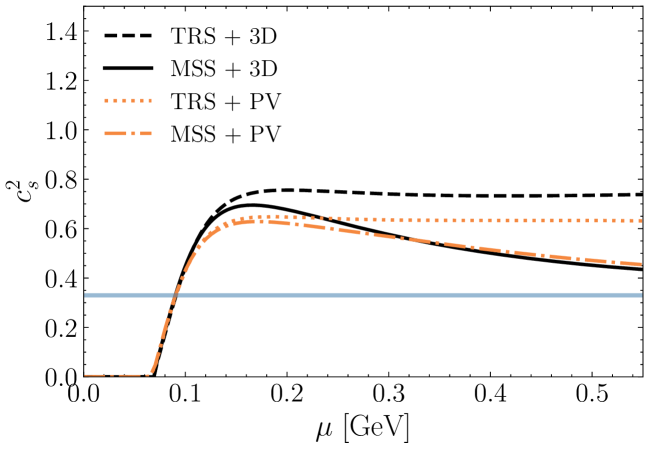
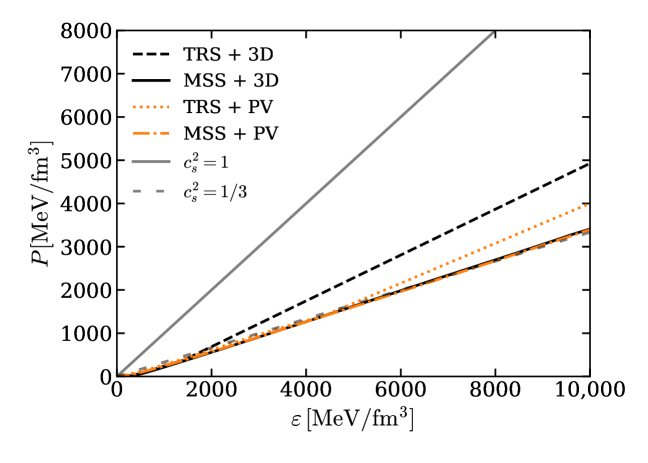
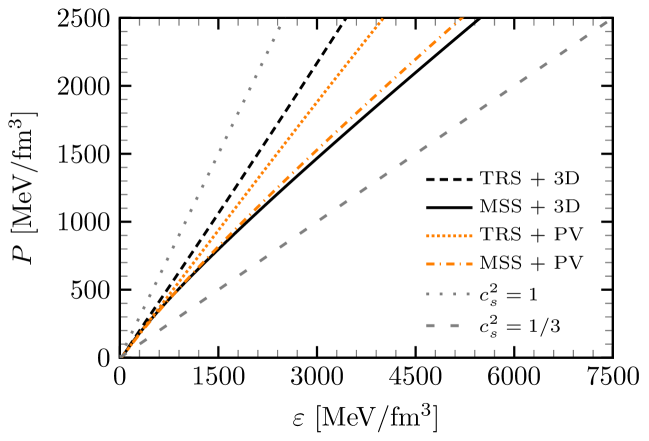
Investigations into the behavior of ultra-dense matter reveal a fascinating evolution in the speed of sound as density increases. Utilizing the Medium Separation Scheme (MSS), calculations demonstrate that the speed of sound initially surges, peaking at approximately 1.0 to 1.2 times the speed of light, before gradually diminishing and approaching the theoretical conformal limit of \frac{1}{3} at extremely high densities. This behavior stands in stark contrast to results obtained through traditional computational schemes, which consistently fail to converge towards a stable, physically plausible limit. The MSS, therefore, provides a more robust and realistic model of dense matter, accurately predicting its compressibility and offering crucial insights into the exotic states of matter potentially existing within neutron stars and other extreme astrophysical environments.
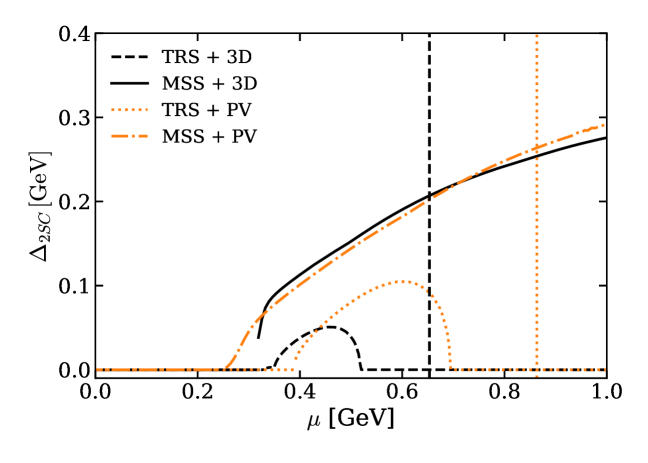
Investigations utilizing the Medium Separation Scheme (MSS) reveal a nuanced picture of dense matter behavior, yielding an equation of state characterized by reduced stiffness at high densities – a result consistent with theoretical expectations and observational constraints. This softening arises alongside a monotonic increase in the diquark condensate as the chemical potential increases, indicating a growing tendency for quarks to pair up. Notably, this consistent growth differentiates the MSS from conventional calculation methods, which often fail to demonstrate this behavior and instead predict more rigid equations of state at comparable densities. The MSS’s ability to accurately model both the softening of the equation of state and the diquark condensate’s evolution suggests a more realistic depiction of the complex interactions governing matter under extreme conditions, offering valuable insights into the properties of neutron stars and the quark-gluon plasma.
The pursuit of understanding dense quark matter, as detailed in this research, highlights a fundamental principle: a system’s behavior is inextricably linked to its underlying structure. Attempts to model the equation of state and, crucially, the speed of sound, require a holistic approach to regularization. As Georg Wilhelm Friedrich Hegel observed, “The truth is the whole.” This rings particularly true when dealing with complex systems like those explored via Lattice QCD; modularity in calculations, while appealing, proves illusory without a consistent framework – a ‘medium separation scheme’ – to contextualize the interactions. If the system survives on duct tape, it’s probably overengineered, attempting to address symptoms rather than the core structural inconsistencies.
Beyond the Horizon
The pursuit of the conformal limit in dense quark matter, as illuminated by this work, reveals a subtle truth: regularization is not merely a technical detail, but a statement about the underlying physics. The ‘medium separation scheme’ offers a path towards consistent treatment of finite density effects, yet it simultaneously highlights the inherent difficulty in cleanly isolating the ‘medium’ from the vacuum. Every simplification of the interaction, every truncation of the expansion, carries a cost – a potential distortion of the emergent behavior. The question is not whether the conformal limit is broken, but how it is broken, and what that breakage reveals about the structure of strongly coupled matter.
Future investigations will undoubtedly refine these effective models and leverage the increasing precision of Lattice QCD calculations. However, a complete understanding demands a broader perspective. The equation of state and the speed of sound are merely observable consequences; the deeper challenge lies in mapping the microscopic interactions onto the macroscopic properties. Specifically, the role of diquark condensation, while hinted at, remains incompletely understood – is it a fundamental property, or an artifact of the chosen regularization scheme?
Ultimately, this research serves as a reminder that elegance in theoretical physics is not achieved through complexity, but through parsimony. The goal is not to build ever-more-intricate models, but to identify the minimal set of ingredients necessary to capture the essential physics. The conformal limit, even when violated, offers a crucial benchmark-a test of whether these ingredients are sufficient, or if a more radical rethinking of the fundamental structure is required.
Original article: https://arxiv.org/pdf/2602.05796.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- How to Unlock the Mines in Cookie Run: Kingdom
- Solo Leveling: Ranking the 6 Most Powerful Characters in the Jeju Island Arc
- Gold Rate Forecast
- Bitcoin Frenzy: The Presales That Will Make You Richer Than Your Ex’s New Partner! 💸
- Bitcoin’s Big Oopsie: Is It Time to Panic Sell? 🚨💸
- Most Underrated Loot Spots On Dam Battlegrounds In ARC Raiders
- Gears of War: E-Day Returning Weapon Wish List
- The Saddest Deaths In Demon Slayer
- How to Find & Evolve Cleffa in Pokemon Legends Z-A
- All Games Coming To Game Pass In 2025
2026-02-07 01:28