Beyond L2: Scaling Transformer Attention with Lp Norms

by

Author: Denis Avetisyan

A new approach to normalizing attention mechanisms in Transformer models uses Lp norms to improve training stability and accelerate convergence.

The analysis of per-parameter validation loss, aggregated across multiple folds, demonstrates the model’s consistent convergence and provides a robust estimate of generalization performance.
The analysis of per-parameter validation loss, aggregated across multiple folds, demonstrates the model’s consistent convergence and provides a robust estimate of generalization performance.

This review details the generalization of QKNorm using the Lp norm, demonstrating enhanced performance across various Transformer architectures.

Maintaining stable training in neural transformers often requires careful normalization of query and key vectors, yet existing approaches are typically limited to Euclidean norms. This paper, ‘Enhanced QKNorm normalization for neural transformers with the Lp norm’, proposes a generalized QKNorm scheme leveraging the flexibility of the L_p norm, allowing for non-Euclidean normalization. Experimental results demonstrate that this approach can improve convergence and performance on attention-based tasks. Could this generalization unlock further advancements in the training and scalability of transformer models for complex applications?

Attention’s Inner Workings: Beyond the Hype

Modern natural language processing owes much of its current success to the Transformer architecture, which fundamentally reimagines how sequential data is processed. Unlike recurrent neural networks that process words one at a time, Transformers utilize attention mechanisms to assess the relationships between all words in a sequence simultaneously. This allows the model to weigh the importance of different input elements – determining which words are most relevant to others – when constructing representations of the text. By focusing on these relationships, attention mechanisms enable Transformers to capture long-range dependencies and contextual nuances that were previously difficult to model, leading to significant improvements in tasks like machine translation, text summarization, and question answering. The core innovation lies in its ability to dynamically prioritize information, effectively ‘attending’ to the most pertinent parts of the input when generating an output.

The foundation of the Transformer’s attention mechanism lies in representing each input element not as a single vector, but as three distinct vectors: Query, Key, and Value. This triadic representation allows the model to capture nuanced relationships within the input sequence. The Query vector can be understood as a request for information, while the Key vectors act as labels or identifiers for each element in the sequence. The Value vectors contain the actual information associated with each element. By comparing the Query with each Key – a process that generates attention weights – the model effectively determines which Value vectors are most relevant to the current processing step. This transformation into Query, Key, and Value vectors isn’t merely a mathematical trick; it’s a fundamental shift that allows the model to dynamically focus on different parts of the input, enabling a far more sophisticated understanding of context and relationships than traditional sequential models.

The heart of the attention mechanism lies in calculating ‘attention logits’, scores that quantify the relationship between each element in the input sequence. These logits are computed by taking the dot product of ‘Query’ vectors – representing what the model is currently looking for – with ‘Key’ vectors – representing what each element of the sequence offers. Attention Logits = Query \cdot Key The resulting scores aren’t probabilities yet; instead, they’re raw measurements of relevance. A higher logit indicates a stronger connection, signaling the model to focus more intently on that particular input element. These logits act as weights, determining the contribution of each value vector during the weighted sum that ultimately produces the attention output, but crucially, they undergo a normalization step, typically using a softmax function, to create a probability distribution before being applied.

Stabilizing the Process: QKNorm to the Rescue

QKNorm mitigates attention instability by applying normalization to both the Query and Key vectors prior to the computation of attention weights. Traditional attention mechanisms can suffer from unstable gradients during training, particularly with large input dimensions or complex models. Normalizing these vectors-typically to unit length-ensures that the magnitude of the Query and Key vectors does not disproportionately influence the resulting attention distribution. This process prevents individual dimensions from dominating the attention scores and contributes to more stable gradient flow during backpropagation, ultimately improving the training process and potentially the model’s overall performance. The normalization step is performed element-wise on both Query and Key vectors before calculating the attention scores using a dot product or similar operation.

Lp Norms offer a parameterized approach to vector normalization, allowing for control over the relative importance of individual vector components during attention weight calculation. Unlike fixed norms such as L2 normalization, the Lp Norm generalizes to various norms by adjusting the parameter ‘p’. When p=2, it becomes equivalent to L2 normalization; p=1 results in L1 normalization, promoting sparsity; and as p approaches infinity, the norm approximates the maximum absolute value of the vector components. This flexibility enables QKNorm to adapt the normalization process based on the characteristics of the Query and Key vectors, potentially leading to improved attention stability and performance across different model architectures and datasets.

QKNorm incorporates a learnable scaling factor, denoted as γ, applied post-normalization to the Query and Key vectors. This factor allows the model to dynamically regulate the magnitude of the attention signal during training. Specifically, the scaled Query and Key vectors, Q' = \gamma Q and K' = \gamma K, are used in the attention weight calculation. By adjusting γ through backpropagation, the model can optimize the attention mechanism to mitigate issues arising from excessively large or small attention values, leading to improved gradient flow and enhanced training stability. This dynamic adjustment also offers the potential to improve model performance by allowing the attention mechanism to better focus on relevant features.

Testing the Waters: nanoGPT and Tiny Shakespeare

To facilitate the evaluation of QKNorm, the method was implemented within nanoGPT, a deliberately simplified version of the Transformer architecture. This implementation strategy allowed for focused experimentation and reduced computational overhead compared to utilizing a full-scale model. NanoGPT retains the core principles of Transformer networks-specifically, self-attention mechanisms-while minimizing complexity by reducing the number of layers and parameters. This streamlined approach enabled efficient training and validation runs, isolating the impact of QKNorm on model performance and stability. The nanoGPT architecture used in this study comprised 4 layers, 32 embedding dimensions, and 64 attention heads.

The training and evaluation of QKNorm was conducted using Tiny Shakespeare, a dataset comprising the complete works of William Shakespeare reduced to approximately 1.2MB of text. This corpus was selected not for its size, but for its representativeness of common language patterns and structural complexities found in larger text corpora. Its limited scale allowed for rapid experimentation and efficient validation of QKNorm’s performance without the computational demands of full-scale language modeling datasets. The dataset consists of 967 lines of text, providing sufficient data to assess the impact of normalization techniques on a simplified language modeling task.

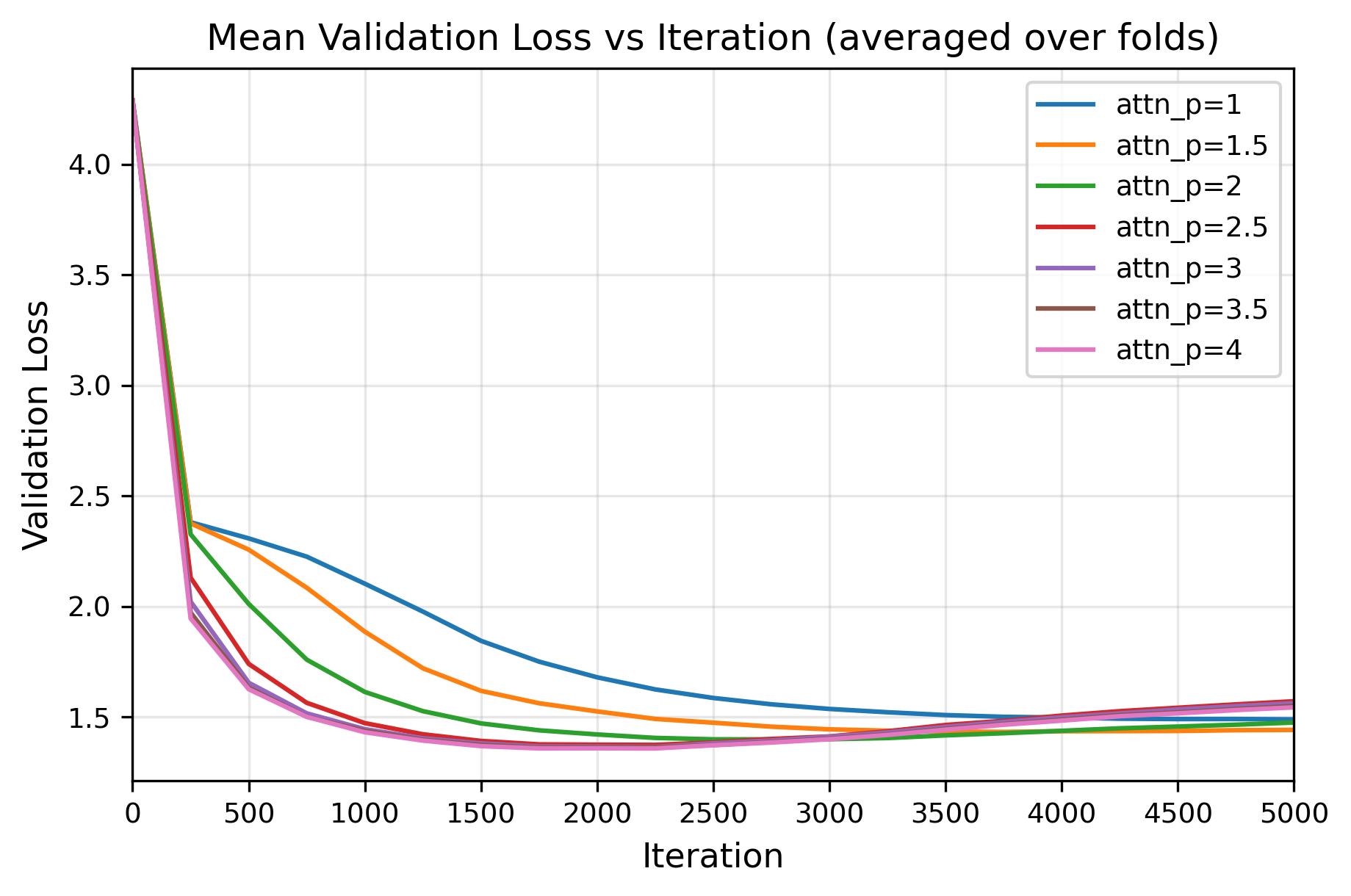
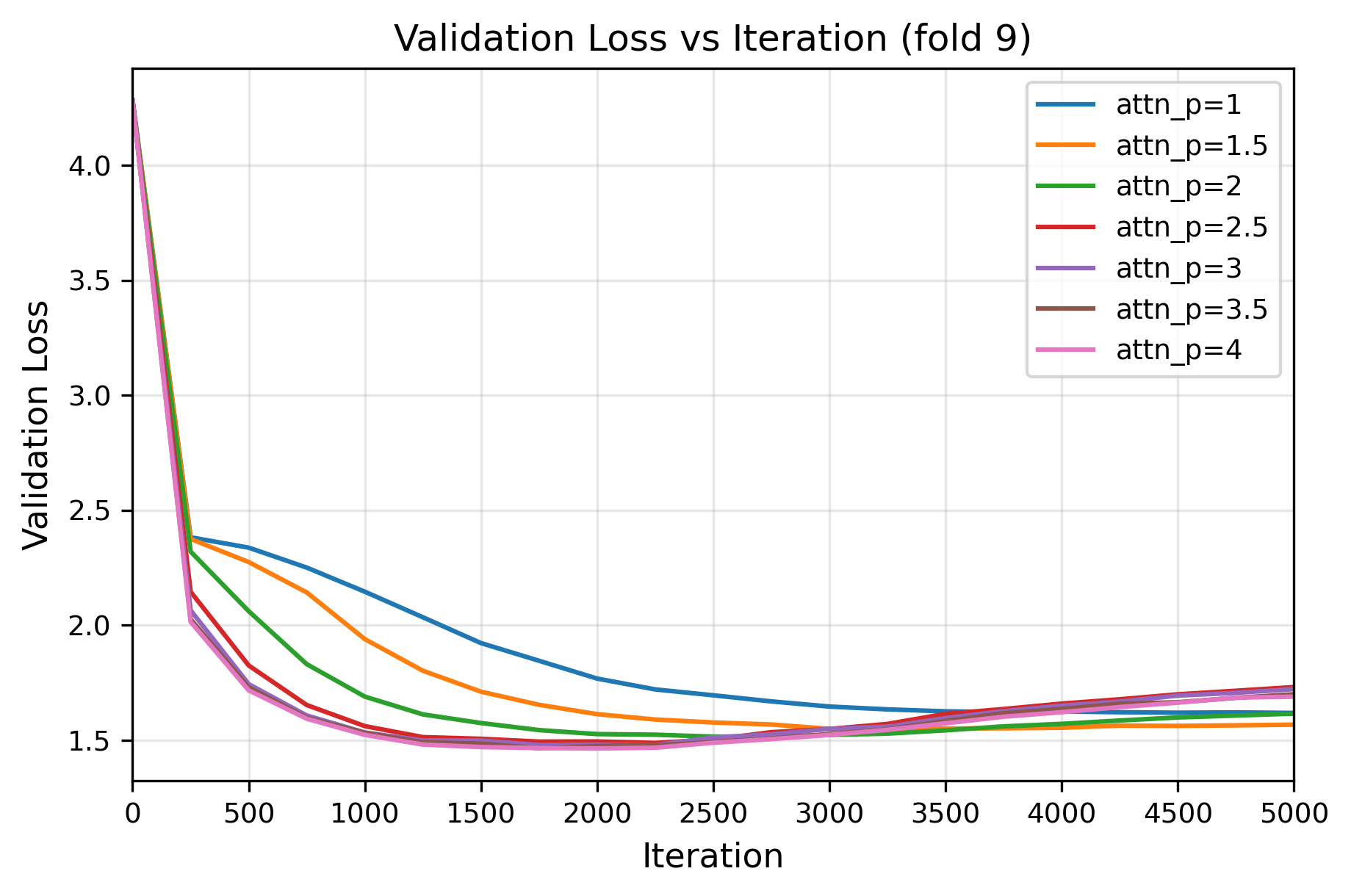
Cross-validation experiments, utilizing the Tiny Shakespeare dataset, were conducted to evaluate QKNorm’s performance. These experiments consistently showed that QKNorm improves training stability and reduces validation loss when compared to standard normalization techniques employing the Euclidean norm. Specifically, a minimum validation loss of 1.357461 was achieved with a value of p=4, indicating an improvement over the 1.40506 validation loss observed with the standard p=2 Euclidean norm. This consistent reduction in validation loss across multiple cross-validation folds demonstrates the efficacy of QKNorm in stabilizing the training process and enhancing model performance.

Comparative analysis within the nanoGPT implementation demonstrated that utilizing the p=4 norm resulted in improved performance as measured by validation loss. Specifically, training with p=4 achieved a validation loss of 1.357461, representing a reduction compared to the 1.40506 validation loss obtained using the standard Euclidean norm, or p=2. This difference indicates that the p=4 norm contributes to a more stable and efficient training process within the tested Transformer architecture and dataset.

Ten-fold cross-validation demonstrates consistent convergence of the validation loss with increasing iterations.
Ten-fold cross-validation demonstrates consistent convergence of the validation loss with increasing iterations.

Beyond the Numbers: Implications for Future Models

The consistent performance gains observed with QKNorm underscore the fundamental importance of normalization techniques in deep learning. Instability during training-manifesting as exploding or vanishing gradients-often hinders the effective learning of complex models. Normalization methods, by rescaling layer activations, mitigate these issues and enable the use of larger learning rates, accelerating convergence. QKNorm’s efficacy demonstrates that carefully designed normalization schemes can not only stabilize the training process but also improve the generalization ability of deep neural networks, allowing them to achieve better performance on unseen data. This suggests that future research into novel normalization strategies holds significant potential for advancing the field and tackling increasingly complex machine learning challenges.

Lp norms represent a versatile mechanism for regulating the scale of weight vectors during deep learning, and consequently, shaping the optimization landscape. By raising the magnitude of these vectors to the power of p and then taking the root, the norm effectively penalizes large weights, promoting more stable and potentially faster convergence. While the L2 norm – where p equals 2 – has long been a standard technique, research indicates that exploring higher values of p can further refine the optimization process. This control over vector magnitudes isn’t merely about preventing exploding gradients; it directly influences the trajectory the optimizer takes through the loss function’s complex topography, potentially leading to solutions with improved generalization performance. The ability to tune this parameter offers a powerful degree of freedom in designing effective deep learning models, allowing for nuanced control over the learning dynamics.

Investigations into the impact of varying Lp norms on deep learning model performance reveal a clear trend: increasing the value of ‘p’ correlates with improvements in validation loss. Specifically, experimentation demonstrated a validation loss of 1.361630 when utilizing p=3.5, a result further supported by values of 1.364543 achieved with p=3, and 1.373479 with p=2.5. This suggests that higher-order Lp norms – those beyond the commonly used L2 norm (p=2) – can effectively refine the optimization process, leading to models that generalize better to unseen data. The observed reduction in validation loss indicates a more robust and accurate model, achieved through a nuanced control of vector magnitudes during training.

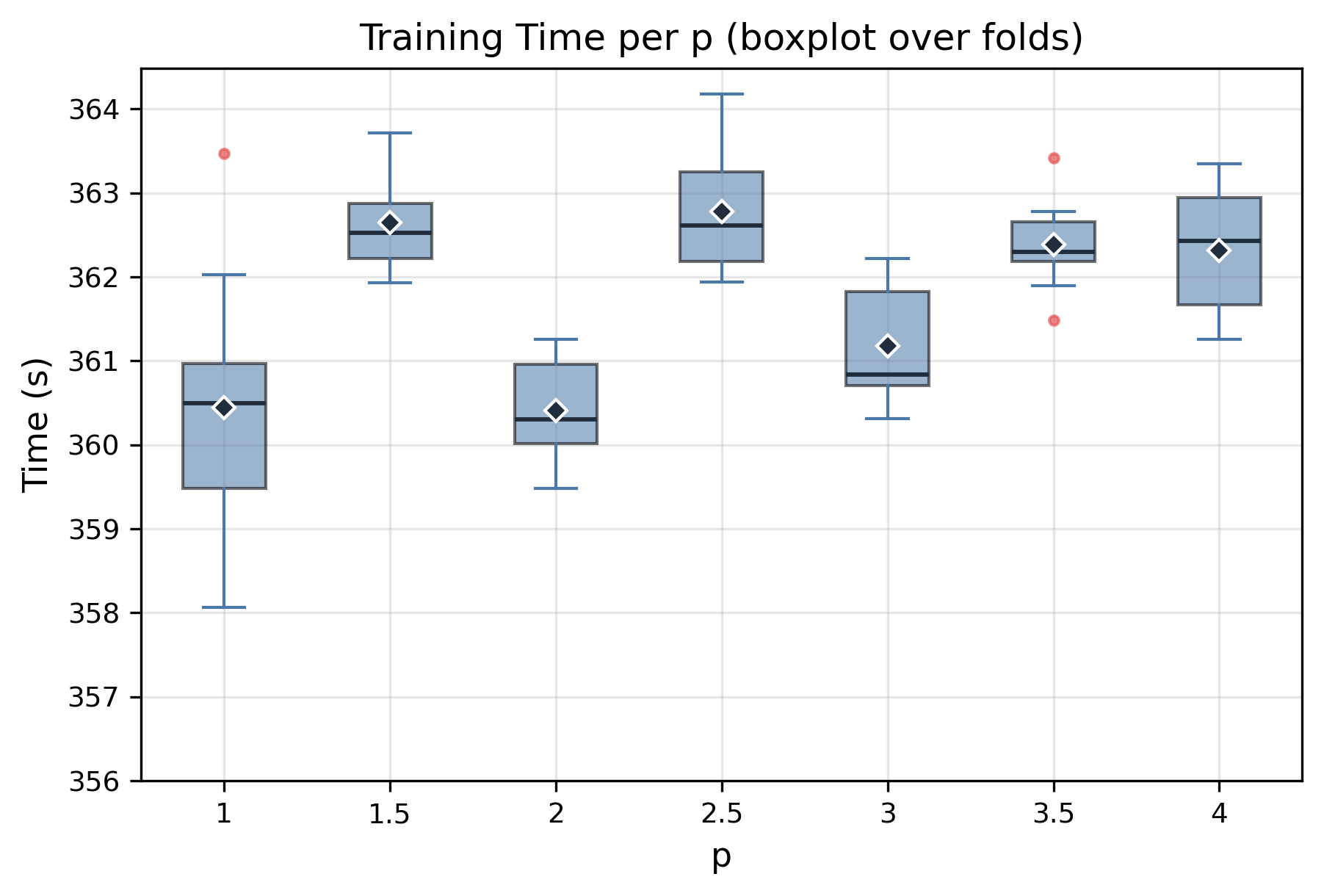
A notable finding from this research is the computational efficiency maintained across varying Lp norm implementations. Despite exploring different values of ‘p’ to optimize validation loss, training time consistently remained within a narrow range of approximately 360 to 363 seconds – exhibiting less than 1% variation. This suggests that the benefits of employing these norms for enhanced model performance are not achieved at the cost of increased computational burden, making them a practical and scalable solution for deep learning applications. The stability in training duration across different norm configurations is particularly significant, indicating a robust and predictable optimization process.

Per-fold training time varied significantly, with the median, interquartile range, and outliers clearly visualized using a box-and-whisker plot where the diamond represents the mean μ.
Per-fold training time varied significantly, with the median, interquartile range, and outliers clearly visualized using a box-and-whisker plot where the diamond represents the mean μ.

The pursuit of elegant normalization schemes, as evidenced by this generalization of QKNorm with the Lp norm, feels predictably optimistic. The authors demonstrate faster convergence and improved performance, but one anticipates the inevitable edge cases production will unearth. It’s a temporary reprieve, really. As Tim Berners-Lee once said, “Anything found accidentally is far more valuable.” This accidental benefit of a more generalized norm might yield initial gains, but the underlying complexity only delays the eventual technical debt. The promise of gradient stability is alluring, yet the history of transformer architectures suggests stability is merely a moving target, not a final state. Documentation will inevitably lag behind the novel failure modes that emerge.

What Lies Ahead?

The substitution of the L2 norm with the Lp norm within QKNorm presents a predictable optimization. Each layer of architectural refinement adds complexity, and with it, a new surface for production anomalies to bloom. The reported gains in convergence speed and performance are, naturally, benchmark-dependent. One anticipates diminishing returns as models scale, and the inevitable emergence of edge cases where the Lp norm introduces unforeseen instability. Tests, after all, are a form of faith, not certainty.

Future work will likely focus on adaptive Lp values-a meta-optimization layer to determine the ‘best’ p for each attention head, or even dynamically during training. This merely shifts the problem, adding another hyperparameter and another potential point of failure. The real question isn’t whether Lp norms can improve performance, but whether the added complexity is worth the marginal gains when a sufficiently motivated dataset inevitably breaks the system on a Monday morning.

It’s a reasonable assumption that other normalization schemes will similarly succumb to this pattern of incremental improvement followed by eventual obsolescence. The pursuit of architectural elegance is a perpetual motion machine; each refinement creates a new form of technical debt. The long-term value will reside not in the normalization itself, but in the monitoring and automated rollback procedures necessary to contain the fallout when, inevitably, it fails.

Original article: https://arxiv.org/pdf/2602.05006.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

See also:

2026-02-07 07:04