Author: Denis Avetisyan
Researchers have developed an algorithm that enhances the safety and reliability of optimal control systems by effectively managing constraints during trajectory planning.
This paper introduces Box-iLQR, an iterative Linear Quadratic Regulator incorporating a logarithmic barrier interior point method for robust constrained optimal control.
Constrained optimal control presents a persistent challenge due to the difficulty of simultaneously ensuring performance and respecting system limitations. This paper introduces a novel approach, ‘Safe Optimal Control using Log Barrier Constrained iLQR’, which seamlessly integrates logarithmic barrier functions into the iterative Linear Quadratic Regulator (iLQR) framework to enforce box constraints on states and controls. By leveraging this interior-point method, the resulting algorithm not only improves convergence and stability but also exhibits natural adaptation near constraint boundaries, effectively transitioning to feedforward control when saturation occurs. Could this barrier-based iLQR offer a robust and efficient solution for a wider range of safety-critical control applications?
The Inherent Complexity of Constrained Dynamical Systems
The pursuit of precise control frequently encounters the inherent complexity of ‘dynamical systems’ – systems whose future behavior is heavily influenced by their current state and a multitude of interacting factors. These systems, ranging from the intricate movements of a robotic arm to the delicate balance of an aircraft in flight, aren’t governed by simple, linear rules. Instead, they exhibit non-linear behaviors, making prediction and control significantly more challenging. Furthermore, real-world applications rarely operate without limitations; actuators have maximum force outputs, joints have range limits, and velocities cannot exceed physical boundaries. These ‘operational limits’ – or constraints – are integral to the problem, demanding control strategies that not only achieve desired performance but also respect these physical boundaries to ensure stability, safety, and prevent damage to the system itself. Ignoring these constraints can render even theoretically optimal control solutions impractical or even dangerous.
Conventional optimization techniques, while powerful in idealized scenarios, frequently falter when confronted with the realities of constrained control systems. These methods often prioritize achieving an optimal solution without fully accounting for physical limitations – the ‘State Constraint’ defining allowable system states, and the ‘Control Constraint’ restricting the magnitude or rate of control inputs. Consequently, the generated control signals can demand operation beyond these boundaries, leading to infeasible solutions that cannot be physically implemented. Even if a solution is mathematically found, disregarding these constraints can induce instability, where the system diverges from its desired trajectory or even becomes dangerously erratic. This necessitates more sophisticated approaches capable of inherently respecting these limitations, ensuring both performance and safety in complex control applications.
The ability to rigorously enforce operational boundaries is paramount when controlling complex systems such as robotic arms and aircraft. Ignoring limitations on speed, force, or orientation can lead to catastrophic failures – a robotic manipulator might collide with its environment, or an aircraft could exceed structural limits during a maneuver. Consequently, control algorithms must not only achieve desired performance but also guarantee that all actions remain within safe and feasible regions of operation. This necessitates advanced techniques that explicitly account for both state – the system’s current condition – and control constraints, ensuring stability and preventing potentially damaging excursions beyond prescribed limits. The pursuit of robust, constraint-aware control is, therefore, not merely an optimization problem, but a fundamental requirement for the dependable functioning of these critical technologies.
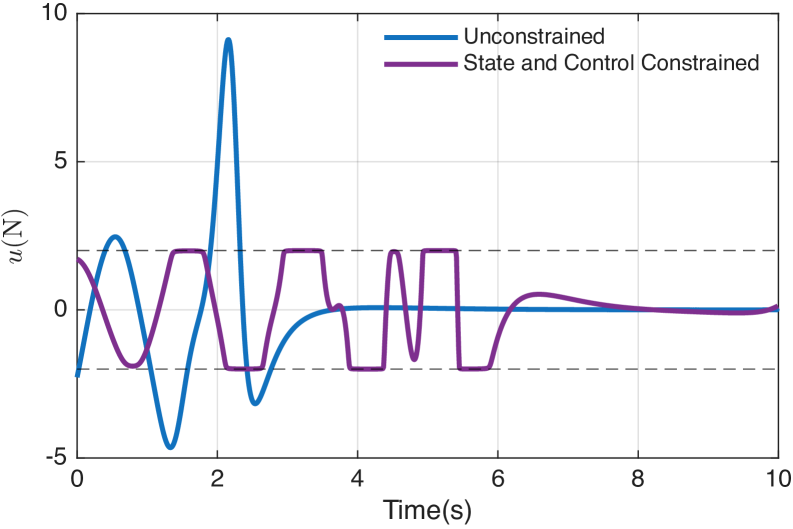
Box-iLQR: A Framework for Constraint Satisfaction
Box-iLQR achieves constrained optimal control by integrating the iterative Linear Quadratic Regulator (iLQR) with an Interior Point Method (IPM). iLQR provides computational efficiency in solving optimal control problems, but does not inherently guarantee constraint satisfaction. The IPM addresses this limitation by systematically searching for solutions strictly within defined constraints. This combination leverages iLQR’s speed for initial trajectory optimization, then refines the solution using the IPM to ensure all constraints are met with a quantifiable margin, resulting in a feasible and efficient control policy.
The Logarithmic Barrier Function is a critical component of Box-iLQR, serving to maintain feasibility during optimization. This function adds a penalty term to the cost function that increases as the optimization variables approach the boundaries of defined constraints. Mathematically, this penalty takes the form of - \gamma \sum_{i} \log(c_i) , where c_i represents the constraint functions and γ is a barrier parameter controlling the strength of the penalty. By minimizing this augmented cost, the optimization process is incentivized to stay within the feasible region – the set of all points satisfying the constraints – and avoids violating system limitations. The barrier parameter γ is typically decreased over iterations to allow the solution to approach the constraint boundaries as the optimization converges.
Box-iLQR maintains operational safety by integrating a logarithmic barrier function into the optimization process. This function introduces a penalty proportional to the inverse logarithm of the distance to the constraint boundaries, discouraging the controller from approaching these limits during trajectory optimization. Consequently, the resulting control strategy is enforced to remain strictly within the defined feasible region, even when faced with complex dynamics or unforeseen disturbances. The strength of the penalty is adjustable, allowing a trade-off between optimality and conservatism, ensuring that the system adheres to safety criteria while striving for performance.
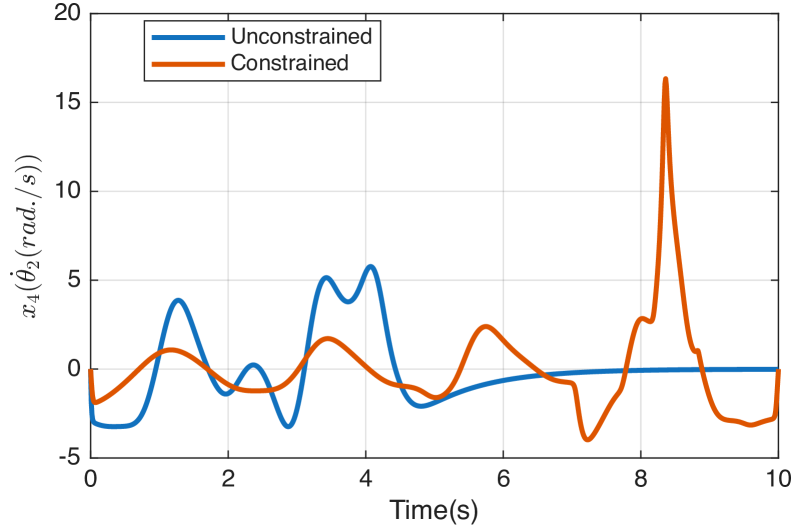
Parameter Tuning: Balancing Performance and Robustness
The Barrier Parameter within the Box-iLQR algorithm functions as a weighting factor for logarithmic barrier terms added to the cost function. Increasing the value of this parameter intensifies the penalty for violating constraints, effectively shrinking the feasible region-the set of states and controls that satisfy all defined limitations. Conversely, a smaller Barrier Parameter allows for a larger feasible region but may result in solutions that approach or occasionally violate constraints. This parameter directly impacts the aggressiveness with which the optimization process satisfies constraints; higher values prioritize constraint satisfaction, potentially at the expense of optimal performance metrics, while lower values prioritize performance with a relaxed adherence to constraints.
Optimal performance and robust stability in constrained optimization are directly linked to parameter selection, particularly when employing techniques like regularization. Regularization introduces a penalty term to the optimization objective, preventing excessively large control actions and mitigating the risk of constraint violations; this is crucial for maintaining stability in dynamic systems. The ‘Barrier Parameter’, when tuned in conjunction with regularization, allows for a trade-off between maximizing performance – achieved by allowing the system to approach constraint boundaries – and ensuring feasible solutions by maintaining a safe distance from those boundaries. Insufficient regularization can lead to aggressive control signals and constraint violations, while excessive regularization can overly constrain the system, resulting in suboptimal performance. Therefore, careful calibration of both parameters is essential for achieving a balance that guarantees both performance and stability.
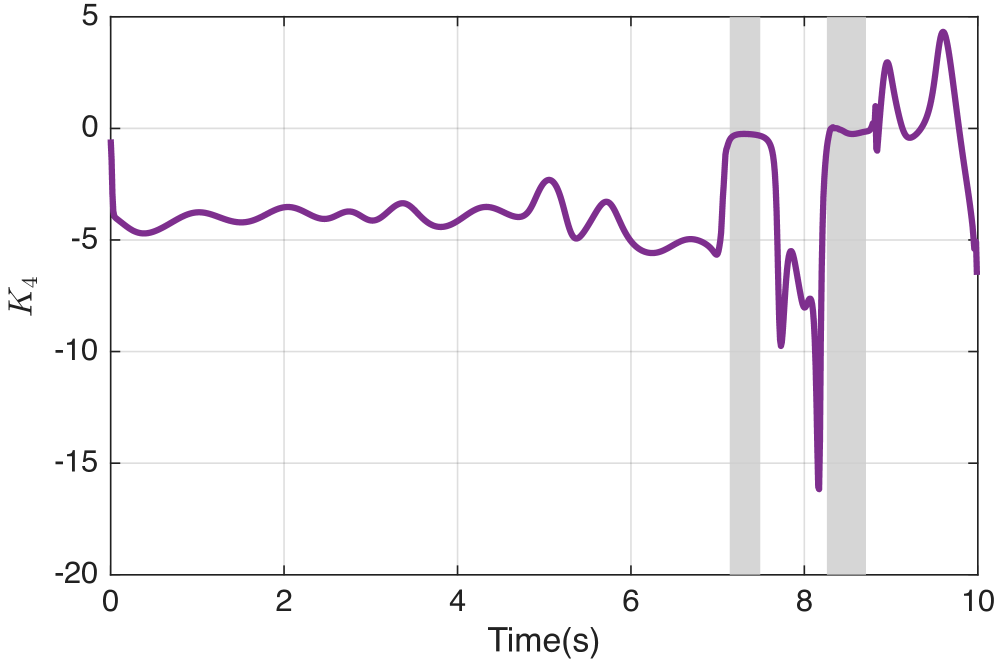
Box-iLQR generates a ‘Feedback Gain’ which, when utilized in a ‘Constraint-Aware Feedback’ control scheme, enables dynamic adjustment of the control signal to maintain operation within defined safety limits. This approach was validated through simulations across three distinct robotic systems – pendulum, cart-pole, and acrobot – consistently achieving 100% convergence to feasible solutions even when subjected to both state and control constraints. This indicates the algorithm’s robustness in handling limitations and consistently finding valid control strategies within the defined operational space.
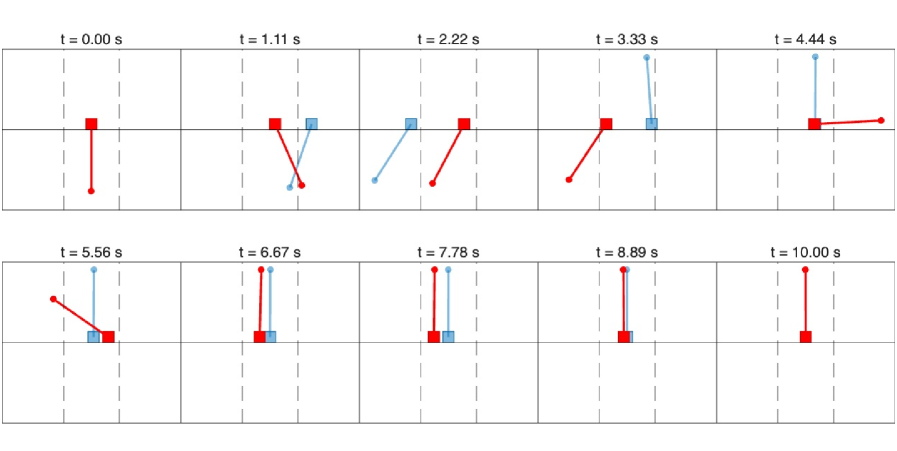
Validation and Broad Applicability to Benchmark Systems
The efficacy of Box-iLQR was systematically assessed using a suite of well-established control benchmarks, beginning with the simple, yet illustrative, Pendulum System and progressing to the more challenging Cart-Pole System before tackling the distinctly nonlinear Acrobot System. These classic problems, frequently employed for algorithm validation, provided a robust testbed for evaluating Box-iLQR’s performance across varying degrees of complexity and dimensionality. Successful implementation on these benchmarks demonstrated the algorithm’s ability to converge to feasible solutions even in scenarios with substantial dynamic challenges, confirming its potential for broader application in control system design and optimization.
Rigorous testing reveals that Box-iLQR consistently achieves feasible and near-optimal solutions in challenging control problems, notably exceeding the performance of unconstrained optimization methods when faced with substantial limitations. The algorithm’s strength lies in its ability to maintain strict adherence to pre-defined boundaries for both state and control variables throughout the entire trajectory optimization process. This constraint satisfaction isn’t merely a byproduct; it’s integral to the solution, ensuring realistic and physically achievable control strategies. Consequently, Box-iLQR demonstrates a robust capacity to navigate complex dynamics while respecting operational limits, establishing it as a reliable approach where constraint handling is paramount.
The versatility of Box-iLQR extends beyond theoretical validation, positioning it as a robust solution for diverse engineering challenges. Simulation results consistently reveal the algorithm’s capacity to navigate complex, non-linear dynamics while respecting operational boundaries; notably, feedback gains diminish predictably as control inputs approach saturation limits, indicating an inherent constraint-aware behavior. This characteristic is particularly crucial in fields like robotics, where actuator limits are pervasive, and aerospace, where maintaining stability within defined parameters is paramount. Furthermore, its applicability reaches into process control systems, allowing for optimized performance even under stringent safety and efficiency requirements, suggesting a broad impact across multiple disciplines requiring precise and reliable control strategies.
The pursuit of robust and demonstrably correct control algorithms, as detailed in this work regarding Box-iLQR, echoes a fundamental principle of mathematical rigor. The integration of a logarithmic barrier interior point method into the iLQR framework isn’t merely an engineering convenience; it’s an assertion of provable stability and convergence. As Albert Einstein observed, “God does not play dice with the universe.” Similarly, this research eschews probabilistic approaches in favor of a deterministic guarantee of constraint satisfaction and optimal trajectory, aligning with a philosophy where solutions are not approximated but proven correct through mathematical foundations. The logarithmic barrier, therefore, isn’t simply a technique, but a mechanism to enforce logical invariants within the optimization process.
The Road Ahead
The integration of logarithmic barrier methods within the iLQR framework, as demonstrated, offers a demonstrable improvement in constrained optimal control. However, the pursuit of algorithmic elegance should not be mistaken for a completed task. The current formulation, while effective, still relies on parameter selection – the barrier parameter itself – which introduces a degree of arbitrariness. A truly robust solution would ideally possess self-tuning capabilities, dynamically adjusting this parameter to maintain stability and convergence without external intervention. The consistency of boundaries, after all, should be intrinsic to the method, not imposed upon it.
Further investigation should address the computational cost associated with interior point methods. While offering improved convergence, the increased complexity necessitates efficient implementation and potentially approximation techniques. The goal isn’t simply to find a solution, but to do so with a demonstrable level of predictability and within acceptable computational limits. The beauty of an algorithm lies not in its ability to navigate complex scenarios, but in the transparency of its constraints.
Ultimately, the field must confront the fundamental question of robustness. How does this approach fare when confronted with model uncertainty or unforeseen disturbances? Theoretical guarantees of stability and convergence, extending beyond the idealized conditions typically assumed, represent the next logical – and most challenging – frontier. The true test of an optimal control algorithm is not its performance in simulation, but its graceful degradation in the face of the inevitable imperfections of reality.
Original article: https://arxiv.org/pdf/2602.05046.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- How to Unlock the Mines in Cookie Run: Kingdom
- Solo Leveling: Ranking the 6 Most Powerful Characters in the Jeju Island Arc
- Gold Rate Forecast
- Bitcoin’s Big Oopsie: Is It Time to Panic Sell? 🚨💸
- Bitcoin Frenzy: The Presales That Will Make You Richer Than Your Ex’s New Partner! 💸
- Most Underrated Loot Spots On Dam Battlegrounds In ARC Raiders
- Gears of War: E-Day Returning Weapon Wish List
- All Games Coming To Game Pass In 2025
- The Saddest Deaths In Demon Slayer
- How to Find & Evolve Cleffa in Pokemon Legends Z-A
2026-02-07 11:21