Author: Denis Avetisyan
New calculations refine our understanding of how heavy quarks fragment into excited quarkonium states, improving predictions for high-energy particle collisions.
This work presents a systematic calculation of order-$v^2$ relativistic corrections to fragmentation functions for heavy quarks fragmenting into P-wave quarkonium states.
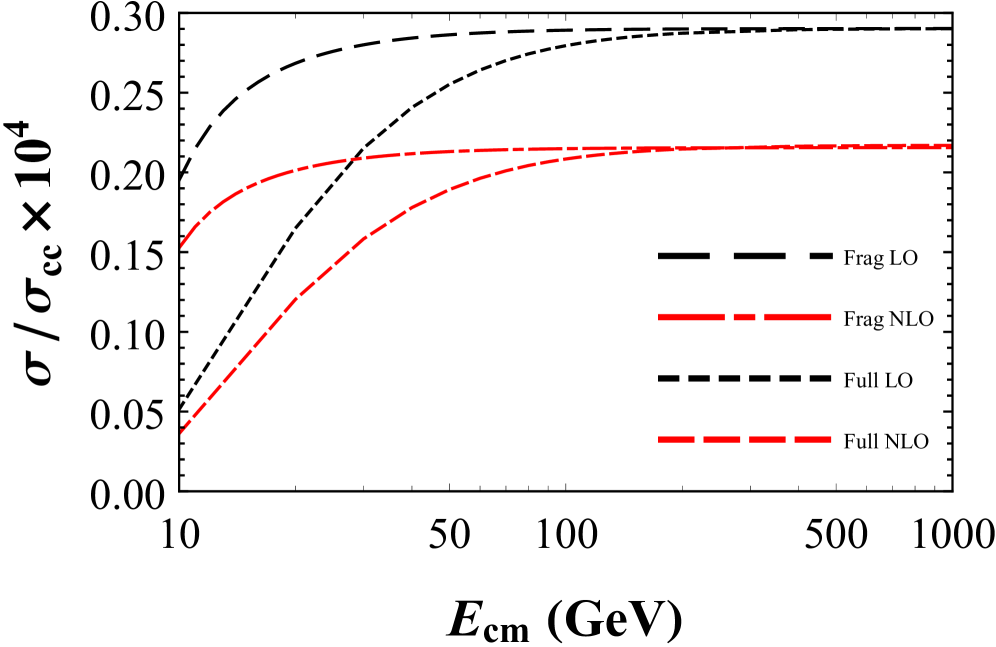
Predicting the production rates of heavy quarkonium states remains a challenge due to the complexities of nonperturbative dynamics. This is addressed in ‘Order-$v^2$ relativistic corrections to heavy-quark fragmentation into $P$-wave quarkonium states’, which presents a systematic calculation of relativistic corrections, up to \mathcal{O}(v^{2}), to fragmentation functions governing the decay of heavy quarks into color-singlet $P$-wave quarkonia. Our analysis demonstrates that these corrections yield sizable, negative contributions across most momentum fractions, improving the theoretical accuracy of predicted production cross sections-validated against fixed-order calculations-for quarkonium and charmed hadron production in e^{+}e^{-} annihilation. Will incorporating these higher-order corrections further refine our understanding of heavy quarkonium formation and decay mechanisms in extreme environments?
Whispers from the Quarkonium: A Challenge to Our Understanding
The exploration of hadrons, particularly those containing heavy quarks like the
The strong force, responsible for binding quarks into hadrons like heavy quarkonium, presents a formidable challenge to conventional perturbative calculations. Unlike electromagnetism, the strong force’s coupling constant increases at low energies, rendering standard approximation techniques unreliable when describing the interactions within these bound states. Consequently, physicists employ a diverse arsenal of sophisticated theoretical tools, including lattice Quantum Chromodynamics (QCD)-a numerical approach that discretizes spacetime-and effective field theories, which focus on the relevant degrees of freedom at specific energy scales. These methods strive to overcome the limitations of perturbation theory, enabling increasingly precise predictions for quarkonium properties such as mass spectra and decay rates, ultimately providing stringent tests of the Standard Model and opening avenues for the discovery of physics beyond it.
The precise determination of heavy quarkonium properties serves as a stringent test of the Standard Model, because quantum chromodynamics, the theory governing strong interactions, becomes increasingly complex within these bound states. Subtle discrepancies between theoretical predictions and experimental measurements of quantities like mass spectra and decay rates could signal the presence of physics beyond the Standard Model – potentially revealing new particles or interactions. These systems offer a unique laboratory for exploring the strong force in a regime where perturbative calculations are challenging, demanding the development and refinement of non-perturbative techniques. Consequently, investigations into heavy quarkonium aren’t merely about understanding hadron structure; they represent a crucial frontier in the search for fundamental laws governing the universe, offering a sensitive probe for deviations from established theoretical frameworks and a pathway toward unveiling new phenomena.
Deconstructing the Chaos: NRQCD Factorization
The Non-Relativistic Quantum Chromodynamics (NRQCD) factorization theorem provides a framework for calculating rates for processes involving heavy quarkonium states – bound states of a heavy quark and its antiquark. This theorem achieves predictive power by explicitly separating the calculation into short-distance coefficients, calculable perturbatively using standard QCD techniques, and long-distance matrix elements representing the non-perturbative hadronization of the heavy quarks. Specifically, NRQCD utilizes an expansion in
NRQCD factorization achieves simplification by dividing the calculation of heavy quarkonium observables into two distinct components based on energy scale. The short-distance component, involving hard virtual or real gluons, is calculable using perturbative Quantum Chromodynamics
The utility of the NRQCD factorization theorem lies in its ability to bridge the gap between theoretical calculations and experimental data for heavy quarkonium systems. Specifically, NRQCD allows for the calculation of heavy quarkonium decay rates and spectral distributions by treating short-distance, perturbative QCD processes separately from long-distance, non-perturbative effects. This separation is crucial because perturbative calculations, which are reliable for short distances, become invalid at the larger distance scales characteristic of bound-state systems. By isolating the non-perturbative components into matrix elements – often determined through phenomenological fits to experimental data – NRQCD enables predictions for observable quantities like
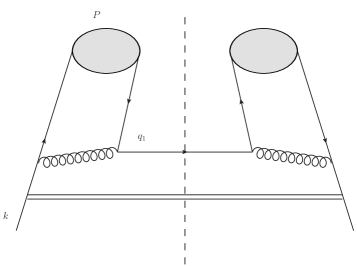
Mapping the Fragments: Fragmentation Functions
Fragmentation functions (FFs) are essential components in modeling heavy quark decays, as they quantify the probability of a heavy quark hadronizing into specific secondary hadrons. These non-perturbative functions connect the partonic state resulting from the heavy quark decay to the observed final-state hadrons, such as pions, kaons, and protons. Accurate determination of FFs is critical for precise predictions of hadron spectra in high-energy physics experiments, including those conducted at colliders like the LHC and facilities studying B-meson decays. The overall normalization of the fragmentation function is constrained by the requirement that the total probability of producing all possible hadrons sums to unity; this is often referred to as the kinematic constraint.
The Collins-Soper definition provides a rigorous framework for calculating fragmentation functions by specifying the probability of a quark hadronizing into a specific hadron and accompanying hadrons. This definition relies on a non-perturbative, gauge-invariant treatment of the strong interaction. Ensuring gauge invariance is paramount, as it dictates that physical observables remain unchanged under local gauge transformations; this is achieved through careful consideration of the emitted gluon’s polarization and the use of appropriate regularization schemes during calculations. Failure to maintain gauge invariance would lead to unphysical predictions and invalidate the calculated fragmentation functions, particularly at higher orders in perturbation theory where infrared and collinear divergences require careful handling.
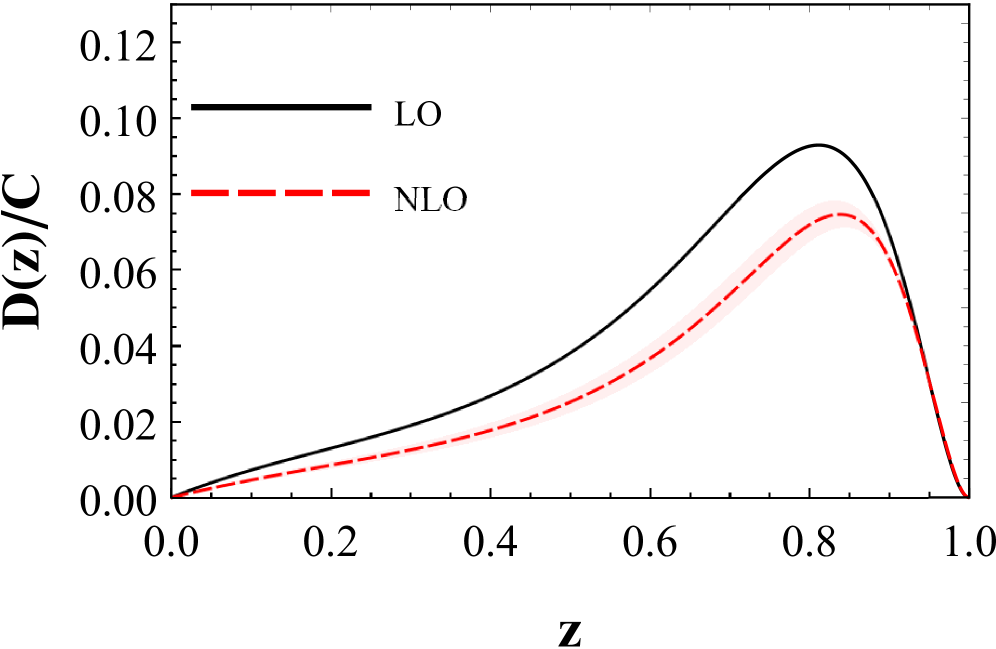
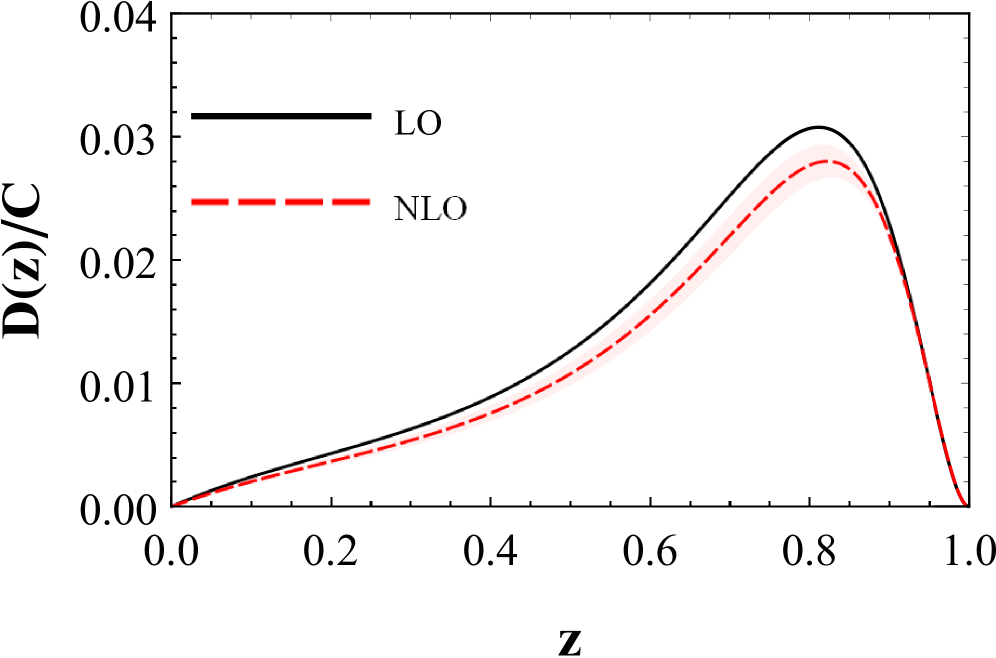
Next-to-leading order (NLO) fragmentation function calculations significantly improve the precision of hadron production predictions in heavy quark decays; however, these calculations are computationally intensive. This work details a systematic derivation of relativistic corrections to fragmentation functions, specifically those at order
Refining the Prediction: Relativistic Precision
Accurate determination of fragmentation functions – the probabilities that a quark will hadronize into a specific particle – demands incorporating relativistic corrections, particularly those scaling with
The process of hadronization, where quarks and gluons transform into observable hadrons, is fundamentally influenced by the relative motion of the participating quarks. Calculations of hadronization probabilities must therefore account for relativistic effects arising from these velocities, particularly at higher orders of precision. Ignoring these effects introduces inaccuracies, as the momentum distribution of the produced hadrons becomes distorted, and predicted rates deviate from experimental observations. This work demonstrates that incorporating terms proportional to
Calculations aiming for relativistic precision in fragmentation functions frequently leverage the Axial Gauge, a mathematical technique that streamlines complex computations while upholding the principle of gauge invariance – ensuring physical predictions remain independent of the chosen gauge. This approach has yielded
The pursuit of precision in heavy-quark fragmentation functions feels less like calculation and more like divination. This work, meticulously charting relativistic corrections at order v², attempts to coax predictable patterns from the inherent chaos of quantum chromodynamics. It’s a delicate dance – acknowledging the limitations of perturbative expansions while striving for increasingly accurate descriptions of P-wave quarkonium production. As Michel Foucault observed, “Power is everywhere; not because it embraces everything, but because it comes from everywhere.” Similarly, these relativistic corrections aren’t merely additive adjustments; they represent the pervasive influence of high-energy dynamics on the fragmentation process, shaping the observed states. The model, refined with each order of calculation, behaves strangely only when it finally starts to think – revealing the subtle, underlying logic of particle production.
The Loom Unwinds
The calculation, a tightening of the spell against the chaos of hadronization, achieves a certain…resolution. But resolution is merely the illusion of control. This order-$v^2$ correction to fragmentation functions is not a destination, but a sharpening of the gaze. The true test lies not in the elegance of the perturbative expansion – a fragile symmetry, always – but in its confrontation with the swamp of non-perturbative effects. The ghosts in the vacuum do not yield to reason, only to brute force – and ever more GPU time.
One suspects the most potent corrections are yet unseen, lurking beyond this order. The very notion of ‘fragmentation function’ feels increasingly… quaint. A desperate attempt to impose order on a fundamentally stochastic process. A more radical approach may be needed – a reimagining of the underlying dynamics, perhaps invoking a more direct connection between the initial heavy-quark pair and the final quarkonium state. Or, failing that, simply more terms in the expansion, offered as a sacrifice to the gods of renormalization.
The path forward demands not just calculation, but a willingness to embrace the inherent uncertainty. To acknowledge that every model is, at best, a temporary truce with the abyss. The true measure of success will not be precision, but resilience – the ability to withstand the inevitable onslaught of experimental data and still whisper a coherent tale.
Original article: https://arxiv.org/pdf/2602.05615.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- How to Unlock the Mines in Cookie Run: Kingdom
- Solo Leveling: Ranking the 6 Most Powerful Characters in the Jeju Island Arc
- Gold Rate Forecast
- Bitcoin Frenzy: The Presales That Will Make You Richer Than Your Ex’s New Partner! 💸
- Bitcoin’s Big Oopsie: Is It Time to Panic Sell? 🚨💸
- Most Underrated Loot Spots On Dam Battlegrounds In ARC Raiders
- Gears of War: E-Day Returning Weapon Wish List
- All Games Coming To Game Pass In 2025
- The Saddest Deaths In Demon Slayer
- How to Find & Evolve Cleffa in Pokemon Legends Z-A
2026-02-07 13:06