Author: Denis Avetisyan
New research constructs a powerful graph model to understand how entanglement dictates the limits of information accessible in evolving universes.
This paper establishes a ‘no-short-cut’ theorem for holographic entropy, ensuring accurate entropy minimization using HRT surfaces in time-dependent spacetimes.
While the holographic entropy cone rigorously classifies entanglement structures in states with a classical gravity dual for static spacetimes, extending this framework to fully time-dependent scenarios has remained a significant challenge due to the complexities of defining relevant extremal surfaces. This paper, ‘Covariant Holographic Entropy Cone’, resolves this issue by constructing a novel graph model directly from the causal structure of entanglement wedges, bypassing the limitations of time-symmetric slices. By proving a crucial “no-short-cut” theorem, we demonstrate that minimizing entropy over these graph cuts is equivalent to considering unions of complete Hubeny-Rangamani-Takayanagi (HRT) surfaces, establishing the equivalence between covariant and static holographic entropy cones. Does this framework pave the way for a deeper understanding of the role of entanglement in the dynamics of spacetime itself?
The Geometry of Entanglement: A Spacetime Tapestry
The AdS-CFT correspondence posits a remarkable duality: a theory of gravity in anti-de Sitter (AdS) space is fundamentally equivalent to a conformal field theory (CFT) living on the boundary of that space. This isn’t merely a mathematical connection, but a deep physical one, suggesting that spacetime itself may emerge from the quantum entanglement within the CFT. Entanglement, a uniquely quantum phenomenon where particles become linked regardless of distance, appears to be geometrically encoded in the higher-dimensional AdS space; regions of the CFT that are highly entangled correspond to areas deeply embedded within the bulk geometry. This framework offers a potential resolution to the long-standing question of how gravity arises from quantum mechanics, hinting that spacetime isn’t a fundamental entity, but rather a manifestation of quantum information and its correlations. The strength of this duality allows physicists to translate problems between the two theories, offering insights into both quantum gravity and strongly coupled quantum field theories, areas traditionally difficult to address with conventional methods.
Establishing a robust understanding of the AdS-CFT correspondence hinges on developing precise tools to map regions on the conformal field theory’s boundary-its ‘surface’-to corresponding volumes within the anti-de Sitter (AdS) space, which represents the gravity side of the duality. This isn’t a simple geometric translation; it demands a sophisticated framework where areas on the boundary are linked to radial directions in the bulk, and vice versa. Researchers employ concepts like the Ryu-Takayanagi formula, which postulates that the entanglement entropy of a boundary region is proportional to the area of its minimal surface in the AdS bulk \mathcal{A}_{min}. This connection allows for the translation of quantum information quantities – such as entanglement – into geometric properties of spacetime, and conversely, provides a pathway to understand the emergence of spacetime geometry from the underlying quantum field theory. The accurate determination of these minimal surfaces, however, presents a significant computational challenge, requiring advanced techniques in differential geometry and numerical relativity.
The intimate link between quantum information and spacetime geometry, revealed through holographic duality, proposes that the very fabric of spacetime emerges from the entanglement of quantum degrees of freedom. This connection isn’t merely a mathematical curiosity; it suggests that the geometric properties of a higher-dimensional anti-de Sitter (AdS) space are directly encoded by the quantum entanglement structure of its lower-dimensional conformal field theory (CFT) boundary. Specifically, regions of the CFT that are highly entangled correspond to connected regions in the AdS bulk, while minimal entanglement implies disconnection. Consequently, studying entanglement patterns within the CFT provides a powerful new lens through which to investigate the emergence of gravity and the fundamental nature of spacetime itself, potentially resolving long-standing puzzles in quantum gravity and offering insights into the information paradox associated with black holes. S = \frac{A}{4G} – the Ryu-Takayanagi formula – exemplifies this connection, relating entanglement entropy to the area of minimal surfaces in the bulk.
Calculating entanglement entropy presents a significant hurdle in fully realizing the implications of the AdS-CFT correspondence. Entanglement entropy, a quantification of the quantum correlations between different parts of a system, isn’t simply a mathematical exercise; it provides a direct link to the geometry of the corresponding anti-de Sitter (AdS) space. Specifically, the amount of entanglement between regions on the boundary of AdS space is believed to be proportional to the area of a minimal surface in the bulk AdS space that connects those regions – a principle known as Ryu-Takayanagi formula. However, accurately computing this area, and thus the entanglement entropy, becomes extraordinarily complex for realistic, interacting quantum field theories. The challenge isn’t merely technical; it requires novel approaches to handle strongly coupled systems where traditional perturbative methods fail, pushing the boundaries of both quantum information theory and theoretical physics to decipher the fundamental relationship between quantum connectedness and the emergence of spacetime.
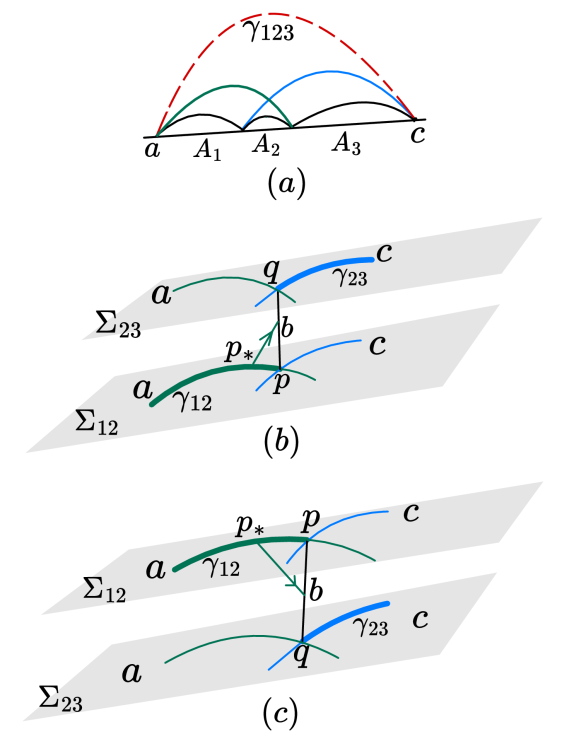
Mapping Entanglement to Geometry: The HRT Prescription
The Ryu-Takayanagi (RT) formula establishes a holographic connection between entanglement entropy in a conformal field theory (CFT) and the area of a minimal surface in the Anti-de Sitter (AdS) space dual to the CFT. Specifically, the entanglement entropy S_A of a region A on the CFT boundary is proportional to the area A_{min} of the minimal surface \gamma_A in the bulk AdS space, whose boundary coincides with the boundary of region A. This is expressed as S_A = \frac{A_{min}}{4G_N}, where G_N is Newton’s constant in the bulk. The formula provides a geometric interpretation of entanglement, linking a quantum information quantity to classical geometry, and crucially, allows for the computation of entanglement entropy in strongly coupled systems where traditional methods fail.
The initial Ryu-Takayanagi formula calculates entanglement entropy for static systems by evaluating the area of a minimal surface in the AdS bulk. To address scenarios involving time-dependent states, the Hubeny-Rangamani-Takayanagi (HRT) formula was developed. This extension replaces the minimal surface with an extremal surface defined on a Cauchy slice – a spatial hypersurface that intersects every timelike curve exactly once. The HRT formula calculates entanglement entropy as S = \frac{A_{ext}}{4G_N}, where A_{ext} is the area of the extremal surface and G_N is Newton’s constant. This approach allows for the calculation of entanglement entropy in dynamic situations where the original Ryu-Takayanagi formula is insufficient.
Calculating holographic entanglement entropy via the Ryu-Takayanagi and Hubeny-Rangamani-Takayanagi formulas necessitates identifying minimal or extremal surfaces within the Anti-de Sitter (AdS) space. This process relies on the Minimal Surface Operator, a computational tool designed to locate these surfaces given boundary conditions. Crucially, the validity of a solution requires adherence to the Null Curvature Condition, which stipulates that the expansion of null geodesics normal to the surface must be non-positive. This condition ensures the surface is indeed a minimal or extremal surface, and prevents physically unrealistic solutions from being considered in the entanglement entropy calculation. The identification of these surfaces often involves solving complex differential equations, and numerical methods are frequently employed to approximate solutions when analytical approaches are intractable.
The uniqueness and validity of minimal and extremal surfaces used in holographic entanglement entropy calculations are ensured by application of the Maximum Principle. This principle, derived from the properties of second-order differential equations in the relevant geometry, dictates that a surface satisfying the appropriate boundary conditions is uniquely determined by minimizing its area functional. Specifically, the Null Curvature Condition, a constraint on the surface’s curvature, facilitates the application of the Maximum Principle. Any surface that does not represent a local minimum of the area functional is demonstrably non-physical and thus excluded as a valid solution for calculating entanglement entropy. This guarantees a well-defined and unambiguous result for the entanglement calculation.
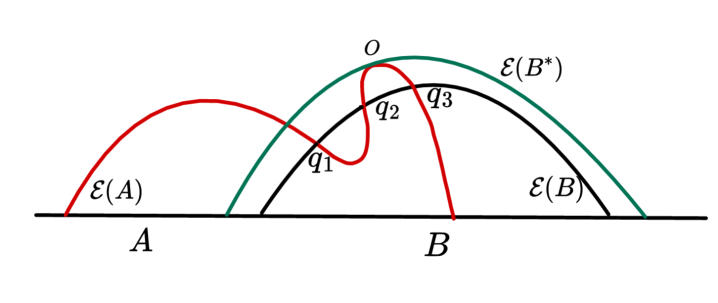
Entanglement’s Architecture: Nesting and the Constraints of No-Shortcuts
Entanglement wedges, defined as the regions of spacetime bounded by minimal surfaces homologous to a given boundary region, exhibit a consistent nesting structure when considering composite regions – that is, regions formed by the union of multiple disjoint subregions. Specifically, the entanglement wedge associated with a larger composite region always contains the entanglement wedges of its constituent subregions. This hierarchical arrangement directly reflects the underlying structure of entanglement; as the boundary region increases in complexity, its corresponding entanglement wedge expands to encompass those of its simpler components. This nesting property isn’t merely observational, but a fundamental constraint dictated by the geometry of spacetime and the holographic principle, implying a direct relationship between the spatial arrangement of entanglement wedges and the quantum information they represent.
The No-Short-Cut Theorem establishes a fundamental constraint on the calculation of entanglement entropy within the AdS/CFT correspondence. Specifically, the theorem proves that determining the entanglement entropy between two regions always requires employing complete HRT (Hubeny-Rangamani-Takayanagi) surfaces – minimal surfaces extending between the boundary regions in the bulk. This rigorously excludes any computational pathways that might utilize incomplete or non-minimal surfaces as ‘shortcuts’, as such constructions would necessarily lead to violations of causality. The theorem’s validity extends beyond specific spacetime dimensions; it is demonstrably true for arbitrary dimensions, reinforcing its status as a core principle governing the relationship between quantum entanglement and spacetime geometry.
The rigorous mathematical foundation of the No-Short-Cut Theorem, combined with the observed nesting of entanglement wedges, provides strong evidence for the holographic principle’s core tenet: that spacetime geometry is fundamentally linked to quantum entanglement. Specifically, the theorem’s insistence on utilizing complete HRT surfaces – and thus avoiding non-physical shortcuts – is consistent with the hierarchical structure revealed by the nested entanglement wedges. This correspondence suggests that the geometric description of spacetime isn’t merely an analogy for quantum information, but rather a direct reflection of its organization; the geometry accurately encodes the relationships and correlations present within the underlying quantum system, and vice-versa. This reinforces the idea that the geometry is not an emergent property, but rather a fundamental aspect of the quantum information itself.
The allowed configurations of entanglement in a holographic system are not arbitrary; geometric constraints derived from the AdS/CFT correspondence restrict their possible arrangements. Specifically, the entanglement entropy of a region is determined by the minimal surface in the bulk AdS space that bounds the region, and this surface’s geometry dictates the permissible entanglement structure. These constraints manifest as the Holographic Entropy Cone, defining the regions of spacetime accessible given knowledge of a particular boundary region’s entanglement. Violations of these constraints would imply either non-local interactions or inconsistencies with the underlying quantum field theory, thus the geometry effectively serves as a map for valid entanglement configurations and their evolution.
The Entropy Cone: Mapping the Limits of Quantum Correlation
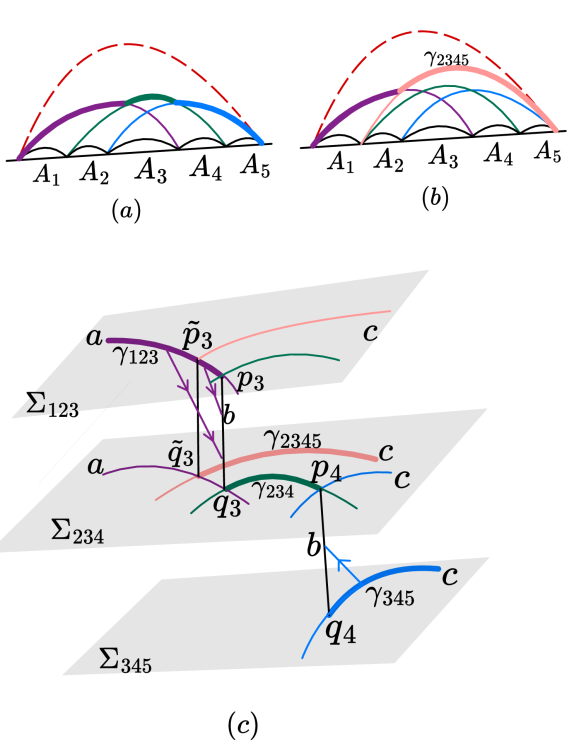
The holographic entropy cone defines the permissible configurations of entropy – a measure of disorder or information – within a boundary region of spacetime. This isn’t merely a theoretical construct; it functions as a stringent limitation on the correlations allowed between quantum particles. Specifically, the cone dictates that the entropy vectors, which mathematically represent the distribution of entanglement, must fall within its boundaries, effectively ruling out certain quantum states as physically impossible. This constraint arises from the holographic principle, suggesting that all information contained within a volume of space can be encoded on its boundary, and thus, the entropy of the interior is fundamentally linked to the correlations on that surface. By precisely mapping the allowed entropy configurations, the holographic entropy cone offers a powerful tool for understanding the interplay between quantum information, gravity, and the very fabric of spacetime, providing a novel lens through which to examine the emergence of physical reality.
Recent research establishes a surprising rigidity in the structure of quantum entanglement within the framework of holography. The study demonstrates that the holographic entropy cone – a geometric representation of allowed entropy configurations for regions of spacetime – remains consistent regardless of whether considered for static or dynamically evolving states. This isomorphism between the time-dependent and static cones proves the entropy cone is fundamentally polyhedral, meaning its boundaries are defined by a finite number of facets. This finding isn’t merely a mathematical curiosity; it strongly suggests a deep and previously unappreciated connection between the geometry of spacetime and the underlying structure of quantum information, bolstering the holographic principle’s assertion that gravity emerges from quantum entanglement.
The Complete Graph Model provides a novel framework for interpreting the holographic entropy cone, translating complex quantum relationships into a visually accessible network. This model represents each region on the boundary of spacetime as a node, with edges denoting entanglement between those regions; the strength of entanglement is reflected in the edge weights. By mapping the allowed entropy vectors onto this network, researchers can gain intuitive insights into the constraints imposed by quantum mechanics on spacetime geometry. This approach not only simplifies the visualization of high-dimensional entropy spaces but also facilitates the exploration of potential extensions to the cone, offering a powerful tool for investigating the fundamental connection between quantum information and the holographic principle. The network structure allows for systematic analysis of entanglement patterns and the identification of key relationships that govern the behavior of quantum systems in curved spacetime.
The established relationship between the structure of quantum information and the geometry of spacetime offers compelling support for the holographic principle, a theoretical framework suggesting that gravity emerges from quantum entanglement. This work demonstrates that the constraints governing allowed quantum correlations – as mapped by the holographic entropy cone – exhibit a surprising rigidity, mirroring the structure of static systems even when considering dynamic states. This suggests that the fundamental degrees of freedom describing spacetime might be encoded on a lower-dimensional boundary, much like a hologram encodes a three-dimensional image. Consequently, the observed geometric properties of spacetime aren’t intrinsic but rather emerge from the complex web of quantum entanglement residing on this boundary, implying a profound interconnectedness between information and the very fabric of reality. The polyhedral nature of the entropy cone further reinforces this idea, hinting at a discrete, rather than continuous, underlying structure to spacetime itself.
The construction of a graph model to represent holographic entropy, as detailed within this work, echoes a fundamental truth about complex systems. It’s not simply about minimizing entropy at a single moment, but tracing its evolution across a dynamic spacetime. As Georg Wilhelm Friedrich Hegel observed, “We do not understand the whole until we understand the parts.” This paper’s no-short-cut theorem, ensuring complete HRT surfaces accurately represent minimal entropy, demonstrates an appreciation for the interconnectedness of these ‘parts’-the entanglement wedges-within the larger system. The careful partitioning and analysis aren’t merely mathematical exercises; they reveal how even complex, time-dependent causal structures adhere to underlying principles of systemic coherence, even as they inevitably age and transform.
The Horizon of Refinement
The construction of a graph model for holographic entropy in time-dependent spacetimes, while a necessary advancement, merely refines the tools for charting decay. Any improvement, even one predicated on rigorous minimization via HRT surfaces and the no-short-cut theorem, ages faster than expected. The demonstrated ability to accurately represent entropy’s evolution doesn’t prevent its inevitable increase, but allows for a more precise measurement of the rate at which information erodes. The model, in essence, maps the unfolding of a system’s limitations, not its transcendence.
Future work will inevitably confront the limitations inherent in partitioning spacetime using entanglement wedges. The very act of defining these wedges, of drawing boundaries around information, introduces an artificial structure onto a fundamentally fluid reality. The true challenge lies not in perfecting the graph model, but in acknowledging its inherent incompleteness-understanding that rollback, the attempt to reconstruct past states, is always a journey back along the arrow of time, never a true return.
The demonstrated success encourages exploration of more complex time-dependent geometries, but a nagging question persists: at what point does increasing fidelity to the model become a distraction from the underlying process of informational loss? Perhaps the most fruitful path lies not in further refinement, but in accepting that the map will always be less informative than the territory it attempts to represent.
Original article: https://arxiv.org/pdf/2602.04888.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- Solo Leveling: Ranking the 6 Most Powerful Characters in the Jeju Island Arc
- How to Unlock the Mines in Cookie Run: Kingdom
- YAPYAP Spell List
- Bitcoin Frenzy: The Presales That Will Make You Richer Than Your Ex’s New Partner! 💸
- Top 8 UFC 5 Perks Every Fighter Should Use
- Gold Rate Forecast
- Gears of War: E-Day Returning Weapon Wish List
- Bitcoin’s Big Oopsie: Is It Time to Panic Sell? 🚨💸
- How to Find & Evolve Cleffa in Pokemon Legends Z-A
- Most Underrated Loot Spots On Dam Battlegrounds In ARC Raiders
2026-02-09 02:09