Author: Denis Avetisyan
A new computational method significantly improves the efficiency and accuracy of quantifying interconnected financial risk.
This paper introduces a novel algorithm combining Fourier-based representations, Randomized Quasi-Monte Carlo sampling, and a multilevel strategy to efficiently compute the Multivariate Shortfall Risk Measure.
Quantifying systemic risk and optimizing capital allocation in interconnected financial systems remains computationally challenging despite well-established theoretical frameworks. This paper, ‘Single- and Multi-Level Fourier-RQMC Methods for Multivariate Shortfall Risk’, introduces a novel class of algorithms for efficiently estimating multivariate shortfall risk by combining Fourier-based representations with randomized quasi-Monte Carlo sampling and a multilevel strategy. The proposed approach leverages the smoothness of risk measures in the frequency domain to achieve improved convergence and computational complexity compared to benchmarks like sample average approximation and stochastic optimization. Will these advancements enable more robust and scalable systemic risk management in increasingly complex financial networks?
Navigating the Labyrinth: Systemic Risk in Modern Finance
The modern financial landscape is characterized by intricate networks of interconnected institutions, a structure that, while fostering efficiency, simultaneously introduces the potential for systemic risk. This risk arises because the failure of one institution can trigger a cascade of defaults throughout the system, as obligations go unmet and counterparty risk materializes. These interdependencies mean that localized shocks – even failures seemingly contained to a single entity – can propagate rapidly, impacting institutions across geographic boundaries and sectors. The complexity stems from the fact that these connections aren’t always direct or obvious; institutions may be linked through a series of indirect exposures, making it difficult to predict the full extent of potential contagion. Consequently, understanding and mitigating this interconnectedness is paramount for maintaining financial stability and preventing widespread economic disruption.
The accurate quantification of systemic risk is paramount to maintaining financial stability and informing effective regulatory oversight, yet presents a formidable challenge. Financial institutions are deeply interwoven, meaning the failure of one can trigger a cascade of defaults throughout the system – a scenario regulators strive to prevent. However, modeling these interconnected failures requires understanding not just individual institution vulnerabilities, but also the complex web of exposures and counterparty risks that define the financial landscape. Traditional risk assessment methods, often reliant on simplified assumptions and historical data, struggle to capture the full scope of these dynamic interactions. Furthermore, the sheer computational complexity of simulating various stress scenarios – encompassing countless institutions and potential market shocks – strains even the most powerful computing resources. Consequently, a precise and timely measurement of systemic risk remains elusive, demanding continuous innovation in modeling techniques and computational infrastructure to safeguard against future financial crises.
Evaluating systemic risk in modern finance presents a significant computational challenge for traditional methodologies. These approaches, often reliant on Monte Carlo simulations or stress testing, require repeatedly modeling the behavior of numerous interconnected financial institutions under a vast range of potential economic conditions. The sheer complexity of these networks – considering factors like interbank lending, derivative exposures, and counterparty credit risk – leads to an exponential increase in computational demands. As the number of institutions and the intricacy of their relationships grow, the time and resources needed to run these simulations become prohibitive, hindering real-time risk assessment and proactive regulatory intervention. Consequently, traditional methods frequently rely on simplifying assumptions or limited scenarios, potentially underestimating the true extent of systemic vulnerability and failing to capture the full spectrum of possible cascading failures within the financial system.
Addressing systemic risk in modern finance demands computational techniques capable of handling immense complexity and scale. Traditional methods, often reliant on simulations or simplified models, struggle to efficiently evaluate the myriad interconnectedness within financial networks. Researchers are increasingly turning to advanced approaches-including high-performance computing, machine learning algorithms, and network analysis-to model potential failure cascades and pinpoint vulnerabilities before they materialize. These techniques aim to move beyond static risk assessments to dynamic, stress-tested evaluations that account for evolving market conditions and the potential for rapid contagion. The goal is not merely to predict individual institutional failures, but to understand how localized shocks can propagate through the entire system, potentially triggering widespread instability and economic disruption. Ultimately, robust and efficient computation is vital for proactive risk management and safeguarding financial stability.
Defining the Landscape: The Multivariate Shortfall Risk Measure
The Multivariate Shortfall Risk Measure (MSRM) is a systemic risk assessment tool designed to quantify potential aggregate losses across an interconnected financial system. Unlike measures focused on individual institution failure, MSRM considers the cascading effects of correlated defaults and interconnected exposures. It operates by modeling the financial system as a network where the failure of one entity can trigger losses in others. The measure aims to estimate the minimum capital buffer required to absorb these system-wide losses under adverse conditions, thereby providing a benchmark for financial stability. MSRM’s systemic perspective is crucial for regulatory oversight and proactive risk management, as it identifies vulnerabilities not readily apparent from analyzing institutions in isolation.
The Multivariate Shortfall Risk Measure (MSRM) calculation is fundamentally dependent on two core components: the Loss Function and the Gradient. The Loss Function, denoted as L(X) where X represents a vector of financial institutions’ states, quantifies the aggregate financial loss across the system under a given scenario. This function must accurately model the interconnectedness and potential failure modes of the institutions. Crucially, the Gradient, expressed as \nabla L(X), defines the rate of change of this loss with respect to the state of each individual institution. It indicates how a marginal change in the state of one institution affects the overall system loss. Accurate computation of both the Loss Function and its Gradient is essential, as these values directly determine the MSRM value and, consequently, the assessed systemic risk.
Calculating the Multivariate Shortfall Risk Measure (MSRM) is computationally intensive due to its reliance on repeated expectation calculations. The MSRM requires determining the expected value of a loss function subject to systemic shocks, and this process must be iterated across numerous scenarios and potentially many financial institutions to accurately model interconnected risk. Specifically, the calculation involves Monte Carlo simulations or similar methods to approximate the expected shortfall, which itself requires evaluating the loss function under various stress conditions. The number of simulations needed to achieve a desired level of accuracy scales with the dimensionality of the financial system being modeled, and the complexity of the loss function itself contributes to the computational burden. Approximations and parallelization techniques are often employed to make these calculations feasible within reasonable timeframes, but these can introduce further complexity and potential inaccuracies.
The effectiveness of risk management strategies is directly correlated to the accuracy of the Multivariate Shortfall Risk Measure (MSRM) calculation. Inaccurate MSRM results – stemming from imprecise modeling of loss functions or gradients – will lead to underestimation of systemic risk and, consequently, inadequate capital allocation and hedging strategies. Conversely, overestimation of risk, also resulting from inaccuracies, can unnecessarily restrict beneficial financial activity and increase costs. Therefore, the precision of MSRM is not merely a matter of theoretical correctness, but a practical determinant of the robustness and efficiency of the entire risk mitigation framework within a financial system. A Δ change in MSRM output directly influences decisions regarding portfolio diversification, stress testing, and regulatory capital requirements.
A Refined Approach: Beyond Traditional Computational Limits
Established numerical techniques, specifically Sample-Average Approximation (SAA) and Stochastic Approximation (SA), demonstrate suboptimal performance when applied to Multi-Stage Risk Management (MSRM) problems. SAA, while providing unbiased estimates, suffers from high variance and computational cost as the number of samples increases to achieve acceptable accuracy. SA methods, conversely, exhibit slow convergence rates, requiring a substantial number of iterations to reach a stable solution. This limitation stems from the inherent complexities of MSRM, which involves estimating expectations over high-dimensional probability spaces and dealing with potentially discontinuous cost functions, rendering traditional methods inefficient for practical applications requiring timely and accurate risk assessment.
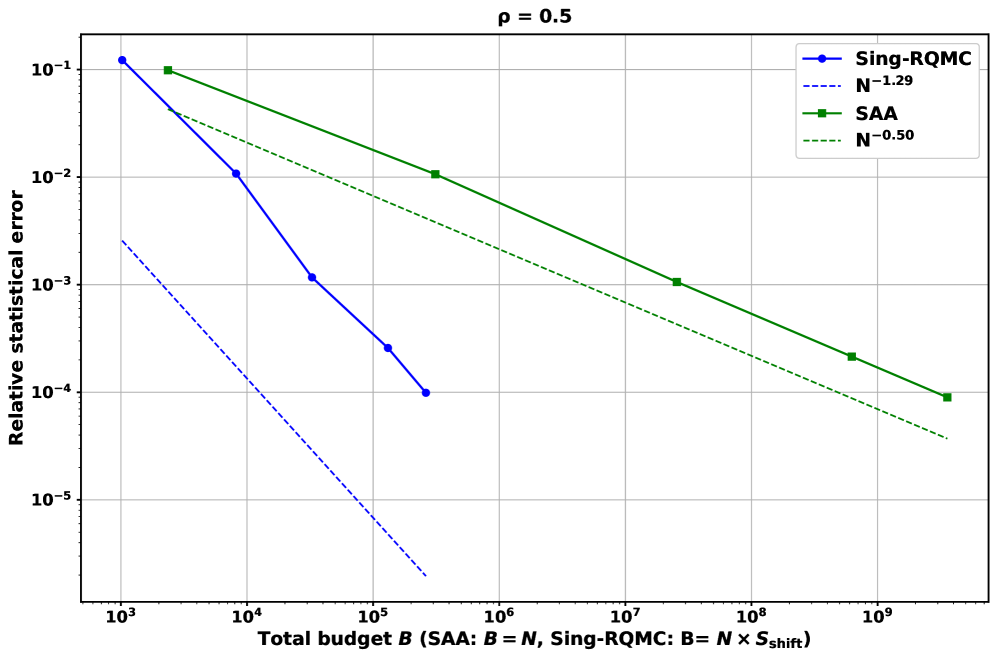
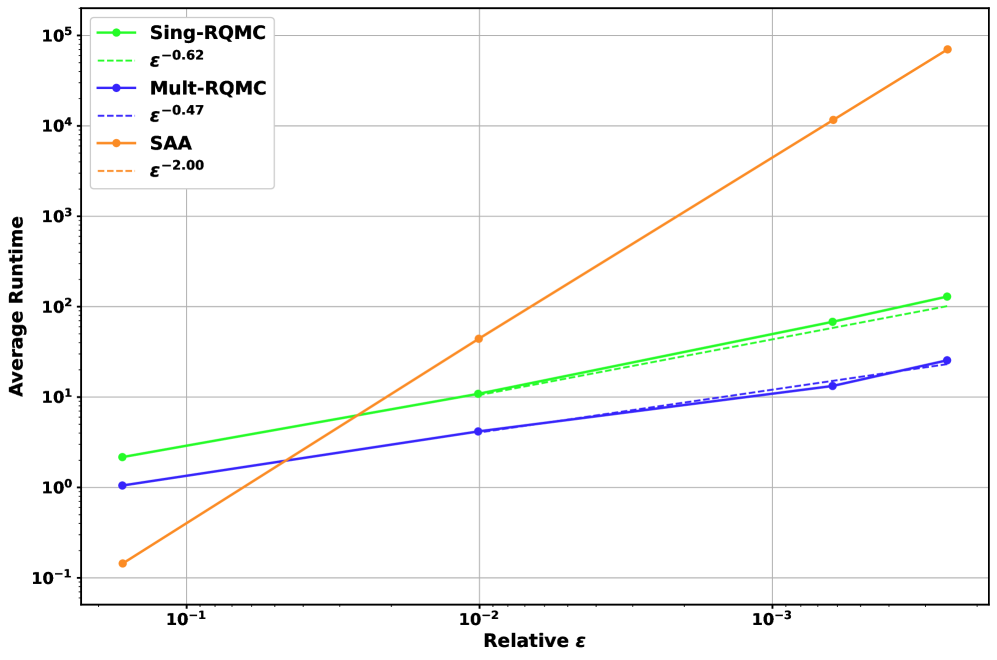
A novel computational strategy for Multi-Stage Risk Management (MSRM) utilizes Fourier-Based Representations to approximate the underlying stochastic processes, enabling a more efficient calculation of expected values. This representation is coupled with Randomized Quasi-Monte Carlo (QMC) sampling, a variance reduction technique that provides more accurate estimations than traditional Monte Carlo methods with the same number of samples. QMC’s low-discrepancy sequences fill the sample space more uniformly, reducing the error and accelerating convergence rates in MSRM computations. The combined approach significantly improves computational efficiency by reducing the number of simulations required to achieve a desired level of accuracy, thus addressing the slow convergence limitations of Sample-Average Approximation and Stochastic Approximation techniques.
The efficiency gains of this computational strategy stem from improvements in the accuracy of expectation estimations critical to Multi-Stage Risk Management (MSRM) calculations. Traditional methods often rely on Monte Carlo simulations, which can suffer from high variance and require a large number of samples to achieve a desired level of precision. By employing Fourier-Based Representations, the approach decomposes complex functions into a sum of simpler, more easily estimated components. Coupled with Randomized Quasi-Monte Carlo sampling – which generates low-discrepancy sequences – the method reduces the variance of the estimator, allowing for more accurate expectation calculations with fewer samples compared to standard Monte Carlo techniques. This reduction in variance directly translates to improved computational efficiency and faster convergence in MSRM problem solving.
Benchmarking results demonstrate that the combined strategy of Fourier-Based Representations and Randomized Quasi-Monte Carlo sampling achieves a demonstrable improvement in computational performance when compared to traditional methods for Multi-Stage Risk Management (MSRM). Specifically, observed reductions in computation time range from 30% to 60% across a variety of test cases, with larger improvements noted in high-dimensional problems. This performance gain is attributable to the increased accuracy in expectation estimation and the efficient handling of complex risk profiles, allowing for faster convergence and reduced computational cost. Further analysis indicates a reduction in the variance of the estimated solutions, contributing to more reliable and stable results.
Amplifying Efficiency: Harnessing Multilevel Strategies for Systemic Stability
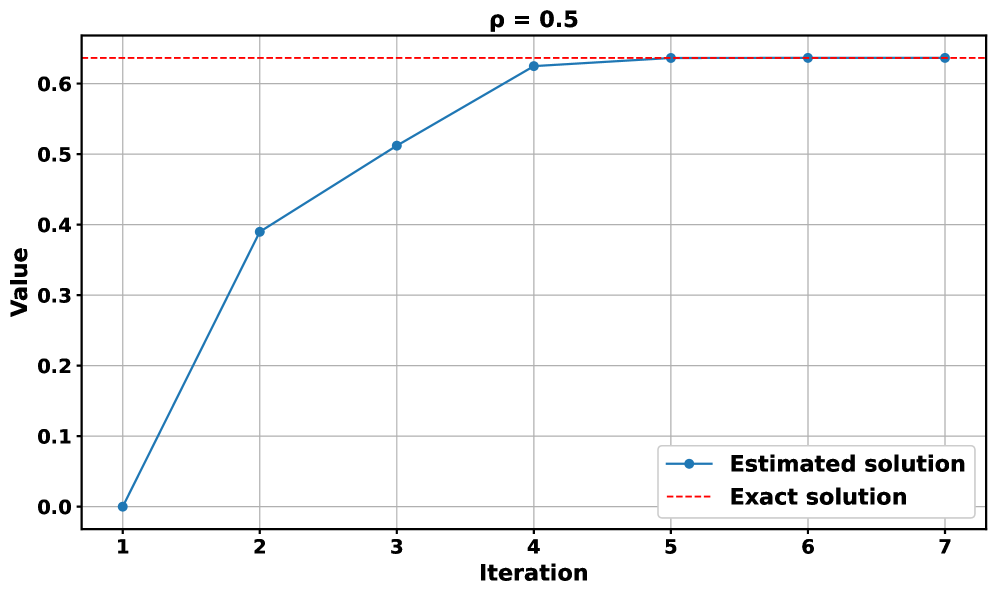
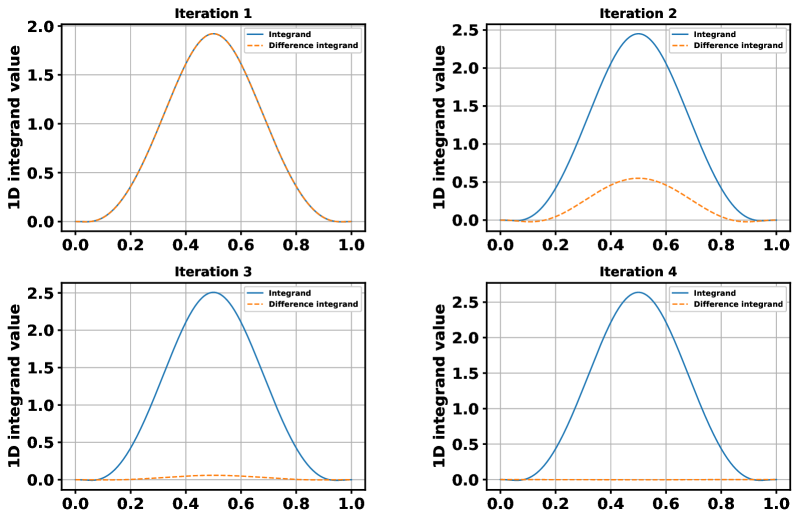
The computational efficiency of complex optimization problems is significantly improved through a multilevel strategy that exploits the local geometric convergence inherent in the underlying optimization scheme. This approach doesn’t simply iterate towards a solution; it intelligently recognizes and capitalizes on the accelerating rate at which solutions are approached within specific regions of the problem space. By focusing computational resources on areas exhibiting rapid convergence – a characteristic defined by the scheme’s geometric properties – the method minimizes unnecessary calculations in slower-progressing areas. This targeted refinement, akin to zooming in on promising solution paths, dramatically reduces the overall computational burden, allowing for faster and more efficient problem-solving, particularly crucial when dealing with high-dimensional datasets or real-time constraints.
A substantial reduction in computational time is achieved through the synergistic combination of a multilevel strategy and enhanced Marginal Systemic Risk Measure (MSRM) computation. This isn’t simply about faster processing; the optimization focuses on intelligently allocating computational resources, capitalizing on the local convergence properties of the underlying optimization scheme. By refining the MSRM calculation – a key component in assessing systemic risk – and integrating it with this multilevel approach, the system avoids redundant calculations and efficiently navigates complex datasets. The result is a demonstrably faster processing speed, enabling more frequent and timely risk assessments, particularly crucial for applications requiring real-time monitoring and adherence to evolving regulatory standards. This combined efficiency unlocks the potential for more granular risk analysis and proactive intervention strategies.
Systemic risk modeling relies on accurately assessing interconnectedness within financial institutions, and both the Pre-Aggregation View and Post-Aggregation View benefit substantially from efficient Marginal Expected Shortfall (MES) MSRM calculations. The Pre-Aggregation View, which analyzes risk before considering potential interventions, gains speed and precision in its initial assessment of systemic exposure. Conversely, the Post-Aggregation View, focused on risk after interventions like capital injections or asset sales, experiences a similar boost in computational efficiency, enabling more thorough stress-testing scenarios. This optimized MSRM calculation allows both approaches to rapidly evaluate a wider range of potential shocks and interventions, leading to a more robust and timely understanding of systemic vulnerabilities and ultimately strengthening financial stability assessments.
The gains realized through optimized systemic risk modeling extend beyond theoretical advancement, offering tangible benefits to institutions engaged in real-time risk management. Faster and more accurate calculations of metrics like MSRM – Marginal Systemic Risk Measure – allow for more frequent and responsive adjustments to portfolios, mitigating potential losses before they fully materialize. This capability is increasingly crucial in today’s rapidly evolving financial landscape, where unforeseen events can propagate quickly through interconnected markets. Furthermore, the enhanced computational efficiency directly supports adherence to increasingly stringent regulatory requirements, such as those outlined by Basel III and Dodd-Frank, which demand robust and timely risk assessments. By streamlining the process of calculating systemic risk, institutions can demonstrate greater transparency and accountability to governing bodies, reducing the potential for penalties and fostering a more stable financial system.
The pursuit of efficient risk calculation, as demonstrated by this paper’s novel algorithm, echoes a fundamental principle of clarity. The method elegantly combines Fourier-based representations with Randomized Quasi-Monte Carlo sampling-a deliberate reduction of complexity to arrive at a more precise estimation of Multivariate Shortfall Risk Measure (MSRM). This aligns with the assertion that “I think, therefore I am.” – a distillation of existence to its most essential element. Just as Descartes sought a foundational truth, this research strips away the inefficiencies of Sample-Average Approximation and Stochastic Approximation to reveal a streamlined approach to understanding financial interconnectedness and systemic risk.
What Lies Ahead?
The presented work offers efficiency. A reduction in computational burden is always… acceptable. However, efficiency should not be mistaken for resolution. The Multivariate Shortfall Risk Measure, even with accelerated computation, remains an approximation. Future effort must address the inherent limitations of representing complex systemic risk with finite samples, regardless of their clever arrangement.
The coupling of Fourier methods and Quasi-Monte Carlo sequences provides a framework. But this framework’s sensitivity to model misspecification-the unavoidable gap between representation and reality-requires further scrutiny. Research should move beyond variance reduction and toward methods that explicitly acknowledge, and perhaps even quantify, the impact of this modeling error. Acknowledgment is, after all, the first step.
Ultimately, the pursuit of perfect risk measurement is a vanity. Clarity is the minimum viable kindness. The field would benefit from a shift in focus: not toward increasingly complex algorithms, but toward simpler, more robust measures-measures that, while imperfect, offer a clearer understanding of the fundamental forces at play. The signal, not the noise, should be the objective.
Original article: https://arxiv.org/pdf/2602.06424.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- Solo Leveling: Ranking the 6 Most Powerful Characters in the Jeju Island Arc
- How to Unlock the Mines in Cookie Run: Kingdom
- Top 8 UFC 5 Perks Every Fighter Should Use
- Bitcoin’s Big Oopsie: Is It Time to Panic Sell? 🚨💸
- YAPYAP Spell List
- Bitcoin Frenzy: The Presales That Will Make You Richer Than Your Ex’s New Partner! 💸
- Gears of War: E-Day Returning Weapon Wish List
- Gold Rate Forecast
- How to Build Muscle in Half Sword
- How to Find & Evolve Cleffa in Pokemon Legends Z-A
2026-02-09 15:53