Beyond Bitcoin: Securing Blockchains for the Quantum Era

by

Author: Denis Avetisyan

A new consensus algorithm leverages quantum key distribution and dynamic node membership to build a blockchain resilient to attacks from future quantum computers.

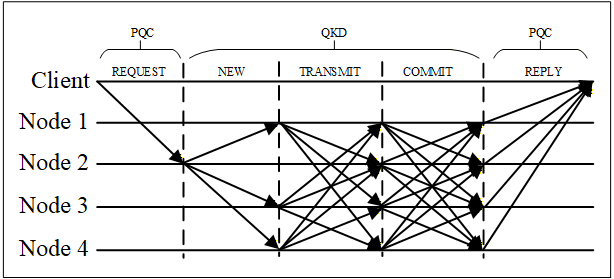
The Quorum-Based Byzantine Fault Tolerance (QDBFT) consensus scheme orchestrates a carefully sequenced message flow, establishing a resilient foundation for distributed systems even in the presence of compromised nodes-a testament to systems designed not to resist decay, but to accommodate it.
The Quorum-Based Byzantine Fault Tolerance (QDBFT) consensus scheme orchestrates a carefully sequenced message flow, establishing a resilient foundation for distributed systems even in the presence of compromised nodes-a testament to systems designed not to resist decay, but to accommodate it.

QDBFT combines Byzantine Fault Tolerance with quantum-secured authentication and automatic node rotation for enhanced efficiency and security.

Conventional blockchain security relies on classical cryptography vulnerable to quantum computing advances, particularly Shor’s algorithm. This motivates the development of quantum-resistant solutions, and we present ‘QDBFT: A Dynamic Consensus Algorithm for Quantum-Secured Blockchain’ to address these challenges. Our approach, QDBFT, integrates Quantum Key Distribution for authenticated inter-node communication with a consistent hash ring-based primary rotation mechanism to enable efficient consensus under dynamic network conditions. Could this combination of techniques provide a viable path toward truly secure and scalable decentralized infrastructures in a post-quantum world?

The Inevitable Erosion of Digital Trust

The foundation of modern digital trust – the methods used to verify authenticity and prevent forgery – is increasingly vulnerable due to advancements in quantum computing. Current digital signatures, which underpin secure online transactions, data storage, and communication, largely rely on mathematical problems that are exceptionally difficult for classical computers to solve, such as factoring large numbers or computing discrete logarithms. However, these problems are precisely the ones that quantum computers, leveraging principles of quantum mechanics, are uniquely equipped to tackle. Algorithms like Shor’s algorithm, specifically designed for quantum computers, offer the theoretical capability to break many of the public-key cryptographic systems currently in use, including RSA and ECC. This poses an existential threat because a sufficiently powerful quantum computer could effectively forge digital signatures, impersonate legitimate entities, and compromise the integrity of digital information on a global scale, necessitating a swift transition to quantum-resistant cryptographic alternatives.

The foundation of modern digital security rests upon the computational difficulty of certain mathematical problems, but algorithms like Shor’s and Grover’s present a looming challenge to this reliance. Shor’s algorithm, specifically, efficiently solves the integer factorization problem – a cornerstone of RSA encryption – and the discrete logarithm problem, utilized in Diffie-Hellman key exchange. This means a quantum computer running Shor’s algorithm could, in theory, break many of the public-key cryptosystems currently protecting sensitive data. While Grover’s algorithm doesn’t completely shatter symmetric encryption like AES, it does reduce the effective key length, requiring significantly larger keys to maintain comparable security levels. The implications are substantial, as these algorithmic advancements demonstrate a clear pathway for quantum computers to undermine the trust inherent in digital communications and data storage, necessitating the development and implementation of post-quantum cryptography.

The foundations of modern digital trust are built upon cryptographic algorithms, many of which are vulnerable to disruption as quantum computing technology matures. Current public-key encryption standards, like RSA and ECC, rely on the computational difficulty of certain mathematical problems – problems that sufficiently powerful quantum computers, leveraging algorithms such as Shor’s, could solve with relative ease. This poses a significant threat, as the decryption of previously secure communications and the forgery of digital signatures become plausible. The potential consequences extend beyond mere data breaches; compromised authenticity could erode trust in financial transactions, critical infrastructure, and governmental systems, necessitating a proactive shift towards quantum-resistant cryptographic alternatives to safeguard data integrity in the approaching quantum era.

The performance evaluation demonstrates the functionality of signature and verification processes.
The performance evaluation demonstrates the functionality of signature and verification processes.

Fortifying the Future: A Quantum-Resistant Shield

Post-Quantum Cryptography (PQC) is a developing field of cryptography focused on constructing cryptographic systems that are secure against both classical computers and future quantum computers. Current widely used public-key cryptographic algorithms, such as RSA and ECC, are vulnerable to attacks from quantum algorithms like Shor’s algorithm. PQC aims to replace these vulnerable schemes with algorithms based on mathematical problems that are believed to be intractable for both classical and quantum computers. This proactive approach is crucial because of the potential for “store now, decrypt later” attacks, where sensitive data encrypted today could be decrypted once sufficiently powerful quantum computers become available. The National Institute of Standards and Technology (NIST) is currently leading an effort to standardize PQC algorithms for widespread adoption.

Post-Quantum Cryptography (PQC) relies on the computational difficulty of specific mathematical problems to provide security. These problems, such as lattice-based cryptography, code-based cryptography, multivariate cryptography, and hash-based signatures, are currently intractable for both classical and known quantum algorithms. The security of these schemes is not based on computational assumptions broken by Shor’s algorithm (which threatens RSA and ECC) or Grover’s algorithm, but instead on the presumed hardness of these alternative mathematical structures. The long-term security offered by PQC stems from the belief that solving these problems requires exponential time or resources, even with the capabilities of a quantum computer, thus protecting data confidentiality and integrity against future computational advancements.

SLH-DSA and ML-DSA are digital signature algorithms currently undergoing standardization as part of the NIST Post-Quantum Cryptography project. Both are based on the hardness of the Shortest Integer Solution (SIS) problem over lattices, a mathematical structure believed to be resistant to attacks from both classical and quantum computers. SLH-DSA offers a relatively small signature size, while ML-DSA prioritizes verification speed. These algorithms are designed as replacements for currently used signature schemes like ECDSA and RSA, which are vulnerable to Shor’s algorithm when executed on a quantum computer. Implementation and security analysis are ongoing to ensure robustness and practicality before widespread adoption, with projected standardization completion anticipated in 2024.

QDBFT: A Consensus Protocol Designed for Endurance

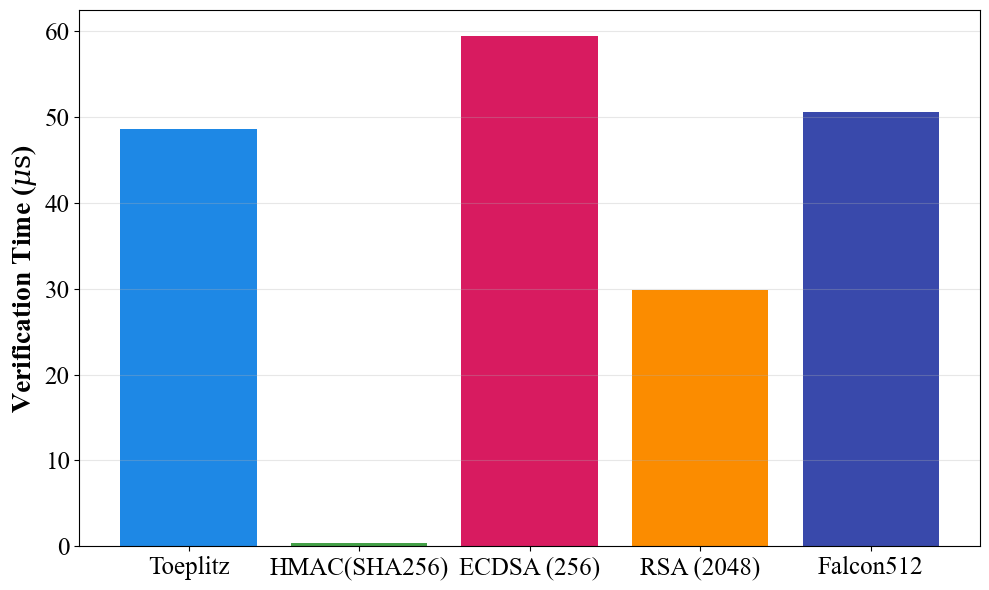
QDBFT represents a new approach to distributed consensus specifically engineered to mitigate threats posed by the advent of quantum computing. Traditional consensus mechanisms, such as Practical Byzantine Fault Tolerance (PBFT), rely on cryptographic primitives vulnerable to attacks from quantum algorithms like Shor’s algorithm. QDBFT addresses this vulnerability by integrating quantum-resistant cryptographic techniques. This design prioritizes maintaining consensus integrity and availability in a post-quantum cryptographic landscape, ensuring the continued secure operation of distributed systems despite advancements in computational power. The protocol achieves this resilience through a combination of Quantum Key Distribution (QKD), Post-Quantum Cryptography (PQC) algorithms, and Toeplitz Hashing, providing multiple layers of defense against potential quantum-based attacks.

QDBFT’s security architecture leverages a multi-layered approach incorporating Quantum Key Distribution (QKD), Post-Quantum Cryptography (PQC) algorithms, and Toeplitz Hashing. QKD is employed for the initial secure distribution of symmetric keys between nodes, establishing a foundation for encrypted communication. Subsequently, PQC algorithms, specifically designed to resist attacks from quantum computers, are utilized for digital signatures and encryption of consensus messages. Toeplitz Hashing is integrated to provide collision resistance and enhance the integrity of the data being exchanged, further mitigating potential vulnerabilities. This combination aims to create a robust defense against both classical and quantum threats to the consensus process.

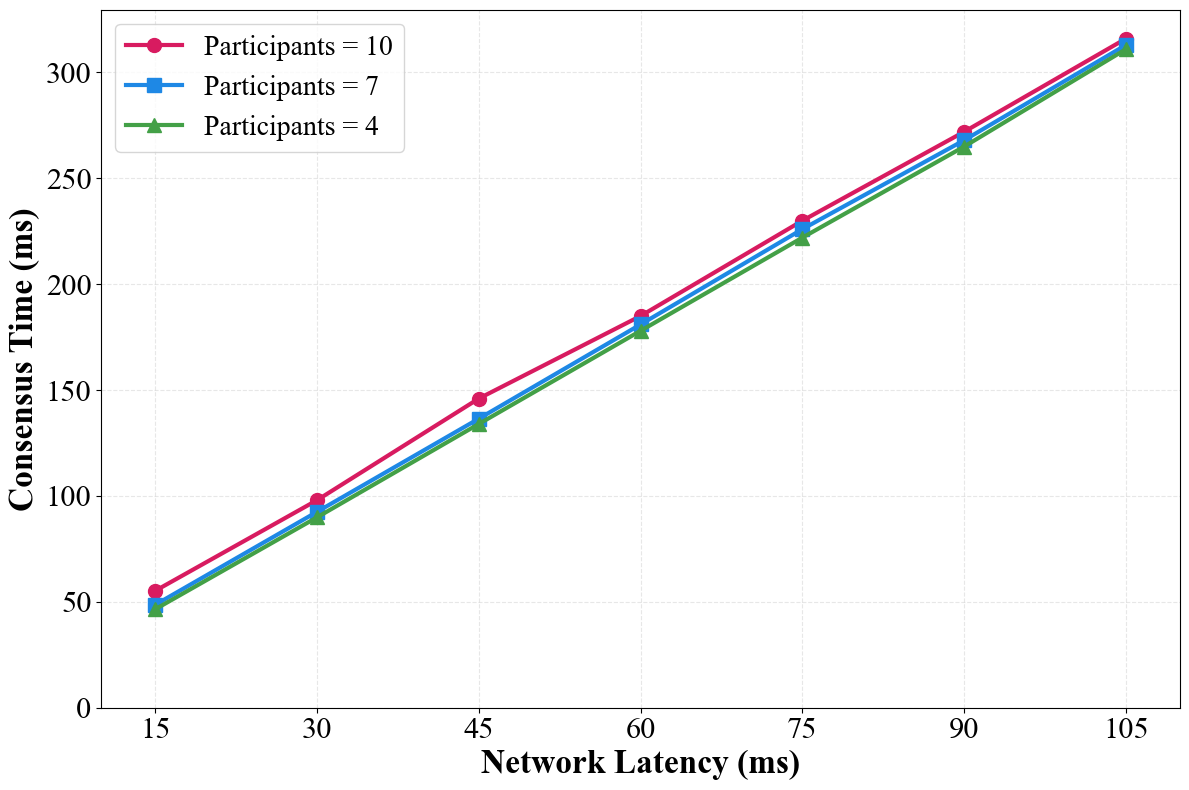
Performance evaluations detailed in this paper demonstrate that QDBFT achieves throughput comparable to Practical Byzantine Fault Tolerance (PBFT). Specifically, testing across varied node counts and network latency conditions reveals similar Transactions Per Second (TPS) rates for both protocols. These results indicate that the integration of quantum-resistant cryptographic primitives does not introduce significant performance degradation relative to established consensus mechanisms. The observed consistency in TPS across different network configurations highlights QDBFT’s scalability and predictable performance characteristics.

QDBFT exhibits a predictable performance overhead characterized by a consensus time approximately three times the measured network latency. This relationship holds consistent across various network configurations and node scales tested. The 3x latency factor represents the time required for the complete consensus process, encompassing message propagation, signature verification, and block finalization. This predictable overhead allows for accurate system performance modeling and facilitates deterministic transaction finality times, crucial for applications requiring time-sensitive operations and reliable performance guarantees.

The QDBFT system utilizes a Consistent Hash Ring to distribute data across nodes, minimizing data movement during node additions or removals and ensuring scalability. This ring structure maps data keys to specific nodes responsible for storing them. Data integrity is further enforced through the use of HMAC (Hash-based Message Authentication Code). HMAC employs a cryptographic hash function and a secret key to generate a message authentication code, allowing verification of both data integrity and authenticity; any alteration to the data will result in a different HMAC value, immediately flagging potential tampering or corruption. This combination of distribution and authentication mechanisms ensures both efficient data management and robust security within the QDBFT framework.

QDBFT consistently demonstrates superior transaction throughput (TPS) and lower consensus latency compared to PBFT, even when scaling the number of nodes or increasing network delays.
QDBFT consistently demonstrates superior transaction throughput (TPS) and lower consensus latency compared to PBFT, even when scaling the number of nodes or increasing network delays.

Extending the Lifespan of Distributed Ledgers

The convergence of Quantum Double Byzantine Fault Tolerance (QDBFT) and blockchain technology addresses a critical vulnerability in contemporary distributed ledgers: susceptibility to attacks from quantum computers. Traditional cryptographic algorithms, which underpin most blockchains, are predicted to be broken by sufficiently powerful quantum systems, potentially compromising the integrity of recorded transactions. QDBFT, a consensus protocol designed to withstand both classical and quantum-based malicious actors, offers a proactive solution. By integrating QDBFT, blockchain systems can establish a quantum-resistant foundation, ensuring the long-term security and immutability of their records. This integration doesn’t simply patch a vulnerability; it fundamentally alters the security paradigm, establishing a system where data remains verifiable and trustworthy even in a post-quantum computing era, and fostering confidence in the enduring reliability of blockchain applications.

The escalating data storage demands of blockchain technology are being addressed through innovative techniques like checkpointing. This process strategically prunes historical data that, while valuable for auditing, isn’t essential for the ongoing operation of the distributed ledger. Instead of continuously expanding the blockchain’s size with every transaction, checkpointing establishes periodic ‘snapshots’ of the system’s state, discarding older data while retaining cryptographic proofs to verify its integrity. This doesn’t compromise security; any past state can be reconstructed from these checkpoints if needed, offering a balance between storage efficiency and complete auditability. By selectively discarding non-essential historical information, checkpointing allows blockchain systems to maintain performance and scalability without sacrificing the immutability that defines the technology.

Blockchain systems, by design, accumulate data with each transaction, leading to ever-increasing storage demands. Checkpointing addresses this challenge through a process of periodically creating a snapshot of the blockchain’s state. This snapshot effectively acts as a trusted anchor point; subsequent data can then be pruned, discarding older, non-essential records without sacrificing the integrity of the ledger. The ability to selectively prune historical data significantly enhances storage efficiency, reducing the computational burden and cost associated with maintaining a continuously growing blockchain. This optimization is crucial for scalability, particularly in applications requiring long-term data retention, as it allows the system to maintain performance and accessibility without being constrained by limitless storage requirements.

The system’s resilience hinges on a carefully constructed interplay between a robust consensus protocol and State Machine Replication (SMR). This combination ensures consistent data replication across multiple nodes, effectively safeguarding against failures. Through SMR, each node maintains an identical copy of the system’s state, and the consensus protocol dictates how these states are updated, even in the presence of malicious actors or network disruptions. By achieving consensus before applying any state change, the system eliminates inconsistencies and guarantees that all nodes converge on the same, accurate record. This architectural approach not only provides fault tolerance-allowing the system to continue operating despite node failures-but also reinforces data consistency, a critical requirement for any distributed ledger technology striving for unwavering reliability and trustworthiness.

The pursuit of resilient systems, as demonstrated by QDBFT, echoes a fundamental truth about all complex architectures. This paper’s focus on dynamic node membership and quantum key distribution isn’t merely about fortifying blockchains against evolving threats; it’s acknowledging the inevitable entropy inherent in any network. As Robert Tarjan once observed, “The most successful algorithms are those that are simple, elegant, and easy to understand.” QDBFT’s design, striving for both security and adaptability, recognizes that longevity isn’t achieved through static perfection, but through graceful evolution – a constant recalibration to maintain integrity in the face of change. The algorithm, much like all systems, will age; the key lies in its ability to do so with resilience and efficiency.

What’s Next?

The proposition of QDBFT, while a logical extension of current efforts, merely relocates the inevitable entropy. Securing consensus via Quantum Key Distribution addresses a specific, and presently looming, vulnerability-the cryptographic decay of established public-key systems. However, the algorithm’s efficacy is predicated on the sustained viability of QKD infrastructure itself-a network inherently susceptible to physical compromise and signal degradation. Uptime, in this context, is a temporary reprieve, not a solved problem.

The dynamic node membership, intended to enhance resilience, introduces a new latency tax. Every rotation, every authentication handshake, exacts a computational cost. The question isn’t whether the system can adapt, but whether the rate of adaptation can outpace the accelerating rate of systemic decay. The algorithm treats nodes as interchangeable components; yet, practical implementations will inevitably exhibit variance in performance and trustworthiness-a reality the model abstracts but cannot eliminate.

Future work will likely focus on minimizing this latency, perhaps through predictive node rotation or adaptive consensus weights. But a more fundamental shift may be required-a move away from attempting to prevent failure and toward embracing graceful degradation. Stability is an illusion cached by time. The true metric isn’t whether a blockchain is impervious to attack, but how elegantly it handles inevitable compromise.

Original article: https://arxiv.org/pdf/2602.11606.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

See also:

2026-02-13 08:59