Uncovering Weak Spots in AI Reasoning

by

Author: Denis Avetisyan

New research reveals a method for pinpointing and correcting flawed logic in large language models without relying on external knowledge sources.

Large language models demonstrate the capacity to revise flawed reasoning steps - specifically, to correct segments initially identified as incorrect - indicating a potential for self-correction during complex problem-solving.
Large language models demonstrate the capacity to revise flawed reasoning steps – specifically, to correct segments initially identified as incorrect – indicating a potential for self-correction during complex problem-solving.

A novel framework, Paraphrastic Probing and Consistency Verification, identifies critical tokens in LLM reasoning paths to improve performance and ensure more reliable inferences.

Despite impressive gains in complex reasoning, large language models remain susceptible to error accumulation and hallucination during multi-step inference. This paper, ‘Finding the Cracks: Improving LLMs Reasoning with Paraphrastic Probing and Consistency Verification’, introduces a novel framework, PPCV, that proactively identifies influential ‘critical tokens’ within an LLM’s reasoning path by leveraging paraphrased questions. PPCV refines these paths without relying on external verification, enhancing consistency and ultimately improving performance. Can this approach of internally probing and verifying reasoning pathways unlock more robust and reliable LLM-driven problem solving?

The Limits of Scale: Decoding Reasoning in Large Language Models

Large Language Models have rapidly advanced natural language processing, showcasing proficiency in tasks like text generation and translation. However, these models often falter when confronted with reasoning challenges that demand more than simple pattern recognition. While adept at identifying correlations within vast datasets, LLMs struggle with multi-step problems requiring logical deduction, planning, or the application of common sense. This limitation stems not from a lack of data, but from the fundamental architecture which prioritizes statistical relationships over genuine understanding; a model can learn to associate concepts without necessarily grasping their underlying causal connections. Consequently, even impressively scaled LLMs can produce nonsensical or incorrect answers when tasked with problems demanding nuanced reasoning, revealing a crucial gap between superficial fluency and true cognitive ability.

Despite the observed correlation between model size and performance gains in Large Language Models, simply increasing scale proves an increasingly inefficient path towards robust reasoning capabilities. While larger models can memorize more facts and exhibit improved pattern recognition, they fundamentally continue to operate by predicting the most probable next token, rather than engaging in genuine causal or logical deduction. This means that scaling alone doesn’t address the core limitation – the models’ inability to reliably process information in a step-by-step, verifiable manner, particularly when confronted with novel or complex problems requiring multiple interconnected inferences. Consequently, diminishing returns are frequently observed, necessitating alternative approaches that focus on enhancing the underlying reasoning mechanisms, rather than solely relying on brute-force memorization and statistical correlation.

Current strategies for enhancing reasoning in Large Language Models, such as Chain-of-Thought Prompting, Self-Consistency, and Tree-of-Thoughts, function as sophisticated scaffolding built upon the foundation of the model’s pre-existing knowledge and pattern recognition abilities. While these techniques encourage models to articulate their reasoning processes or explore multiple solution paths, they don’t fundamentally address limitations in the model’s capacity for genuine logical inference. Consequently, performance remains heavily reliant on the statistical likelihood of correct answers being generated, rather than robust, step-by-step deduction; this inherent dependency introduces a susceptibility to errors, particularly when faced with novel or complex problems that deviate from the patterns encountered during training. The observed improvements, while significant, often represent refinements of existing probabilistic outputs, rather than a leap toward reliable, verifiable reasoning.

Assessing the reasoning capabilities of large language models demands rigorous evaluation through benchmarks such as GSM8K and ARC-Challenge, which consistently reveal deficiencies in complex problem-solving. These tests pinpoint specific areas where current models struggle with multi-step inference and logical deduction. Recent work directly addresses these limitations, showcasing a novel approach that achieves a Pass@1 accuracy of approximately 50.00% on the Math500 dataset – a significant step toward more reliable and accurate reasoning in artificial intelligence. This result suggests that targeted methodologies can substantially improve performance on challenging mathematical problems, offering a promising pathway for overcoming the inherent limitations of scale-based approaches.

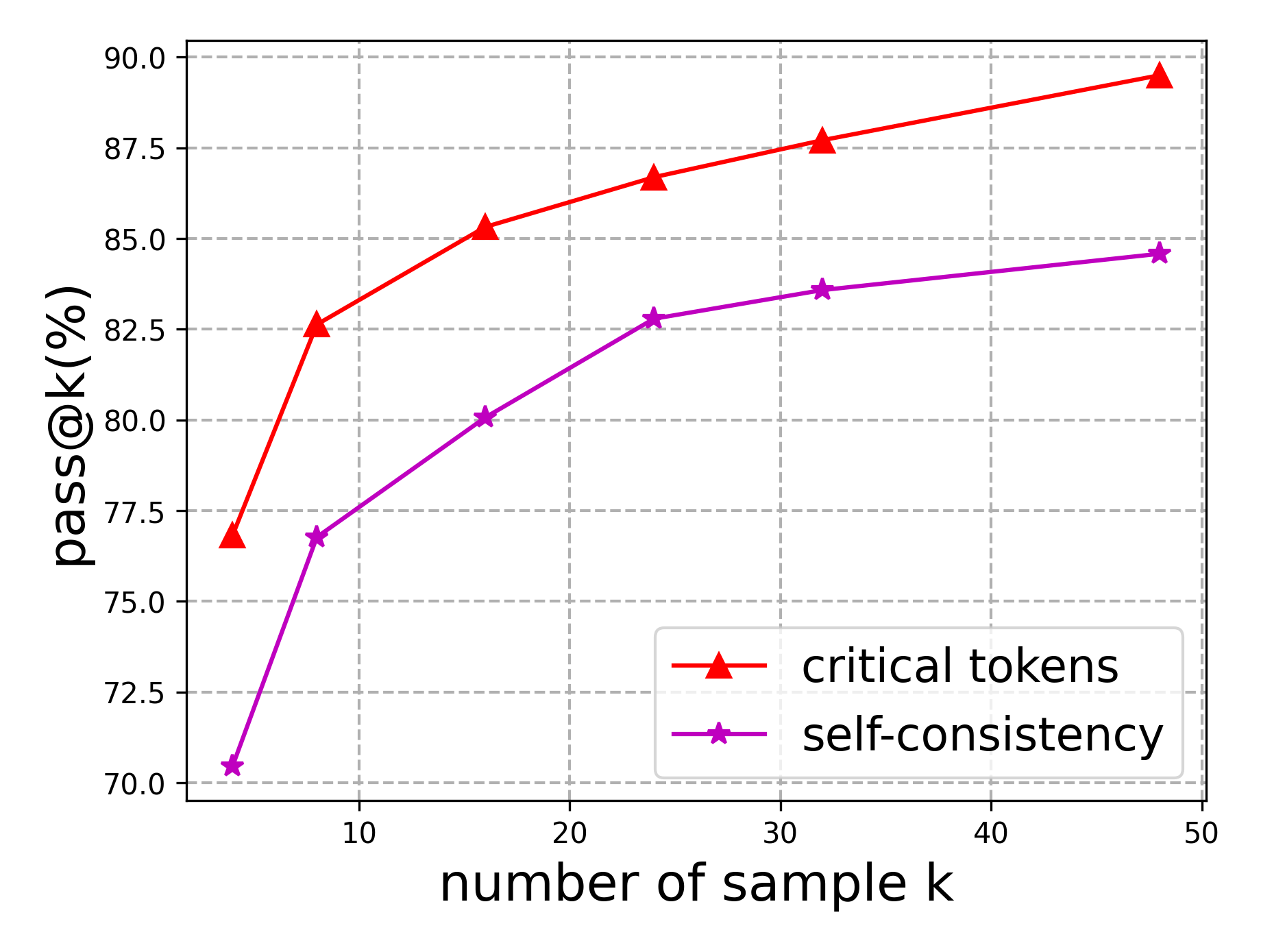
Applying critical tokens and self-consistency decoding significantly improves the reasoning performance of large language models on the GSM8K dataset.
Applying critical tokens and self-consistency decoding significantly improves the reasoning performance of large language models on the GSM8K dataset.

Pinpointing Reasoning Weakness: Isolating Critical Tokens

The Paraphrastic Probing and Consistency Verification framework centers on the identification of ‘Critical Tokens’ within a given reasoning problem. Unlike methods that treat all input tokens equally, this approach specifically isolates those tokens that exert the most significant influence on the Large Language Model’s (LLM) final answer. These critical tokens are not necessarily semantically complex; rather, they are identified by systematically perturbing or replacing individual tokens and observing the resulting change in the LLM’s output. A substantial alteration in the answer following a specific token’s modification indicates its criticality. This targeted analysis allows for a more precise diagnosis of reasoning failures, as it pinpoints the specific elements driving incorrect conclusions, rather than broadly assessing overall performance.

Paraphrastic probing involves generating multiple variations of an initial question to examine the Large Language Model’s (LLM) reasoning process. These paraphrases are not simply semantic rewrites; they are constructed to subtly alter phrasing while preserving the underlying mathematical or knowledge-based problem. By presenting these variations, the system observes how changes in wording affect the LLM’s response, allowing for an assessment of the consistency of its reasoning path. Significant discrepancies between responses to the original question and its paraphrases indicate potential vulnerabilities or reliance on superficial patterns rather than robust logical deduction. This method effectively probes the LLM’s internal reasoning, revealing which aspects of the question are most influential in determining the final answer.

Automatic Prompt Engineering within our framework employs algorithms to generate paraphrased questions designed to rigorously test an LLM’s reasoning process. This process utilizes techniques like back-translation and synonym replacement, governed by constraints that prevent semantic shifts affecting the underlying mathematical or factual problem. The system dynamically adjusts paraphrasing strategies based on initial LLM responses, focusing on variations that maximize information gain regarding critical reasoning steps. This ensures the generated questions are not merely stylistic alterations, but substantive challenges probing the LLM’s reliance on specific cues or potentially flawed logic, without introducing extraneous information or altering the correct solution path.

Analysis of Large Language Model (LLM) responses to paraphrased questions enables the identification of ‘Critical Tokens’ – specific input tokens that exhibit the highest correlation with answer correctness. This is achieved by measuring the change in output probability or the final answer following alterations made to individual tokens within the input. Tokens demonstrating significant impact on the LLM’s output are flagged as critical, indicating their importance in the reasoning process. Consistent identification of these tokens across diverse mathematical and knowledge reasoning benchmarks allows for a focused assessment of LLM vulnerabilities, resulting in performance gains over baseline methods that do not prioritize critical token analysis.

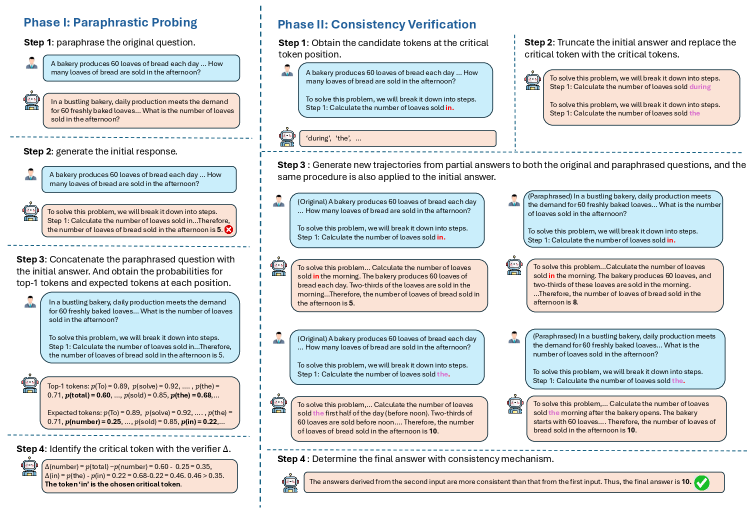
The proposed paraphrastic probing and consistency verification (PPCV) framework enhances reasoning by probing critical tokens with paraphrases, generating alternative reasoning paths, and selecting the most consistent answer based on paraphrase agreement.
The proposed paraphrastic probing and consistency verification (PPCV) framework enhances reasoning by probing critical tokens with paraphrases, generating alternative reasoning paths, and selecting the most consistent answer based on paraphrase agreement.

Verifying Reasoning Paths: Consistency as a Measure of Robustness

The Consistency Score is a quantitative metric used to evaluate the reliability of an LLM’s reasoning process. It is calculated by comparing the responses generated by the model when presented with an original question and a semantically equivalent paraphrased version of the same question. Agreement between these two responses – determined through string matching or semantic similarity analysis – yields the Consistency Score. A score of 1.0 indicates complete agreement, while lower values represent varying degrees of discrepancy. This metric provides an objective assessment of whether the model arrives at the same conclusion regardless of question phrasing, effectively identifying potential vulnerabilities in its reasoning path.

The Consistency Score, a key metric in evaluating LLM reasoning, functions as an indicator of path robustness. A high score – approaching 1.0 – signifies strong alignment between the LLM’s responses to the original and paraphrased prompts, suggesting a stable and reliable reasoning process. Conversely, a low Consistency Score indicates a discrepancy in responses, flagging potential vulnerabilities in the LLM’s logical steps. These low scores do not necessarily denote incorrect answers, but rather highlight areas where the reasoning path is susceptible to minor variations in input phrasing, thus necessitating further analysis and potential refinement of the LLM’s internal logic or training data.

The Consistency Verification method was evaluated across distinct reasoning domains to assess its broad applicability. Performance was measured on both Mathematical Reasoning tasks, requiring numerical computation and problem-solving skills, and Knowledge Reasoning tasks, which demand retrieval and logical inference from factual information. Results indicate the method’s effectiveness is not limited to a specific type of reasoning; consistently high improvements in identifying flawed reasoning paths were observed in both domains. This demonstrates the versatility of the approach and its potential for use in diverse applications requiring robust logical deduction from Large Language Models.

Experimental results demonstrate a statistically significant performance improvement in Large Language Models (LLMs) when inconsistencies within their reasoning paths are identified and rectified. Specifically, applying the Paraphrastic Probing and Consistency Verification framework led to higher accuracy rates on complex mathematical and knowledge reasoning tasks compared to baseline methods. Quantitative analysis revealed a consistent outperformance across diverse problem sets, indicating the framework’s robustness and generalizability. The observed improvements suggest that ensuring logical coherence in the reasoning process is critical for enhancing LLM performance on challenging problems.

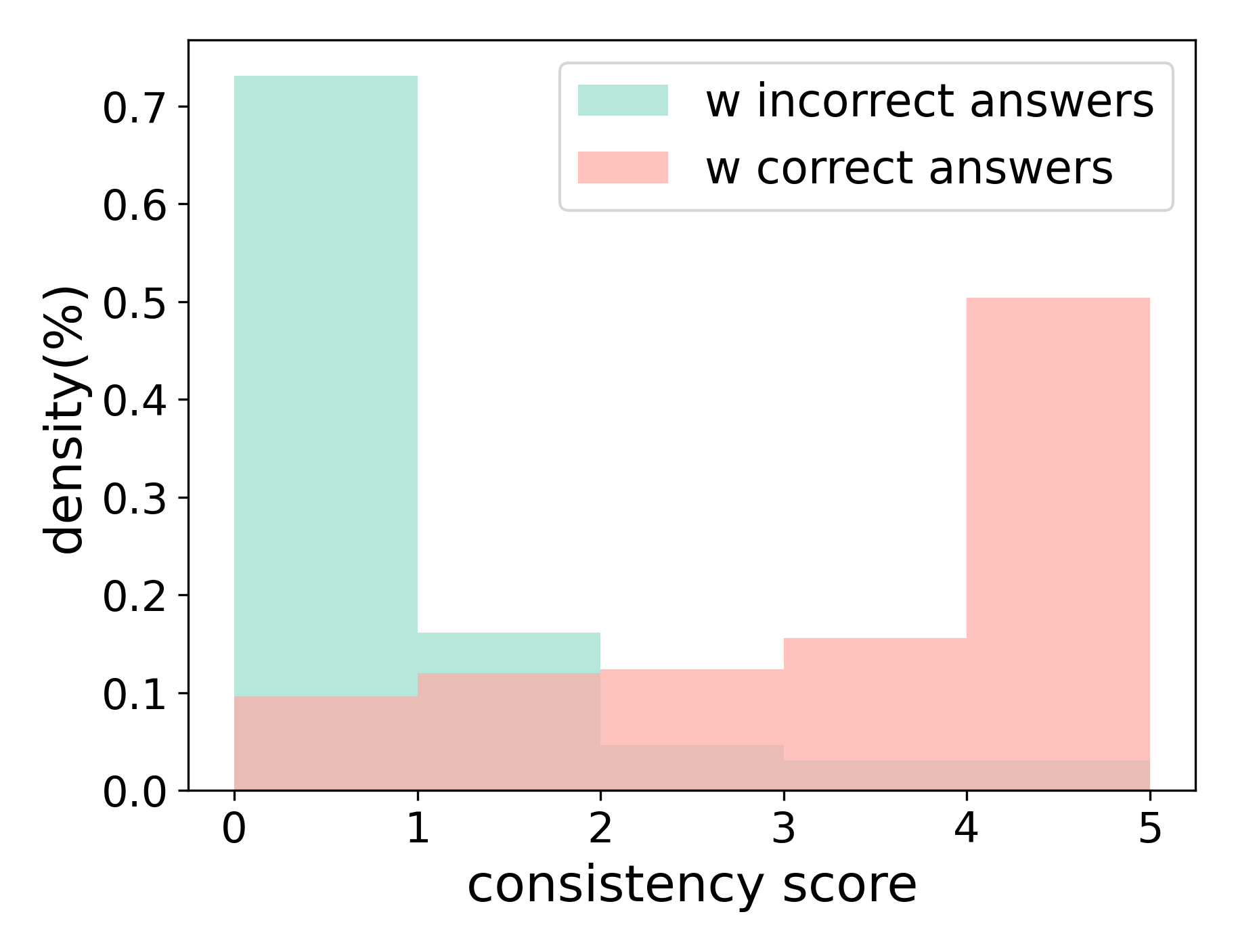
Our method identifies tokens from the Math500 dataset that demonstrably improve LLM reasoning performance and exhibit a stronger correlation with rollout correctness, as evidenced by both immediate (<span class="katex-eq" data-katex-display="false"> \\pm 5\% </span>) and subsequent (<span class="katex-eq" data-katex-display="false"> \\pm 10\% </span>) rollout accuracy, and a distinct distribution of consistency scores for correct versus incorrect answers.
Our method identifies tokens from the Math500 dataset that demonstrably improve LLM reasoning performance and exhibit a stronger correlation with rollout correctness, as evidenced by both immediate ( \\pm 5\% ) and subsequent ( \\pm 10\% ) rollout accuracy, and a distinct distribution of consistency scores for correct versus incorrect answers.

Towards Robust Reasoning: A Shift in Focus

Rather than relying solely on increasing the parameters of large language models, this research demonstrates that focusing on a select few, demonstrably critical tokens during reasoning offers a significantly more efficient path to improved performance. The method hones in on the specific words that most influence the outcome of a logical chain, ensuring internal consistency throughout the process. This targeted approach bypasses the computational expense of scaling model size, achieving enhanced reasoning capabilities with a leaner framework. By prioritizing the reliability of these pivotal tokens, the system exhibits a greater capacity for accurate and dependable conclusions, suggesting a shift towards quality of reasoning rather than sheer quantitative power.

The developed framework offers a significant advancement in the pursuit of transparent artificial intelligence by providing researchers with a means to dissect the reasoning processes within large language models. Instead of treating these models as ‘black boxes’, this approach allows for the identification of specific points of failure or inconsistency in their logic. By pinpointing these critical junctures, developers can move beyond simply improving performance metrics and begin to address the why behind a model’s decisions. This capability is crucial not only for debugging errors but also for building trust in AI systems, particularly in high-stakes applications where explainability is paramount. The resulting insights promise to facilitate the creation of more interpretable models, fostering a deeper understanding of their capabilities and limitations and ultimately paving the way for more reliable and responsible AI.

Investigations are now shifting toward broadening the scope of this reasoning framework beyond its initial applications. Researchers intend to assess its efficacy across diverse cognitive tasks, including commonsense reasoning, spatial reasoning, and temporal inference, to determine the generality of its approach. Simultaneously, efforts are underway to automate the process of inconsistency detection and resolution, moving beyond manual analysis. This includes developing algorithms capable of proactively identifying potential logical fallacies within an LLM’s reasoning chain and implementing self-corrective mechanisms to enhance the reliability of its conclusions, ultimately striving for LLMs that exhibit not just intelligence, but also demonstrable trustworthiness and robustness.

The development of large language models strives not merely for increased computational power, but for a fundamental shift towards dependable artificial intelligence. Current research prioritizes building LLMs capable of confidently navigating intricate challenges, a goal substantiated by consistently surpassing established benchmarks and achieving state-of-the-art performance across a spectrum of reasoning tasks. This focus on reliability transcends simple accuracy; it aims for systems that consistently deliver robust solutions, minimizing errors and fostering trust in their outputs – ultimately paving the way for LLMs to become invaluable tools in fields demanding precision and sound judgment.

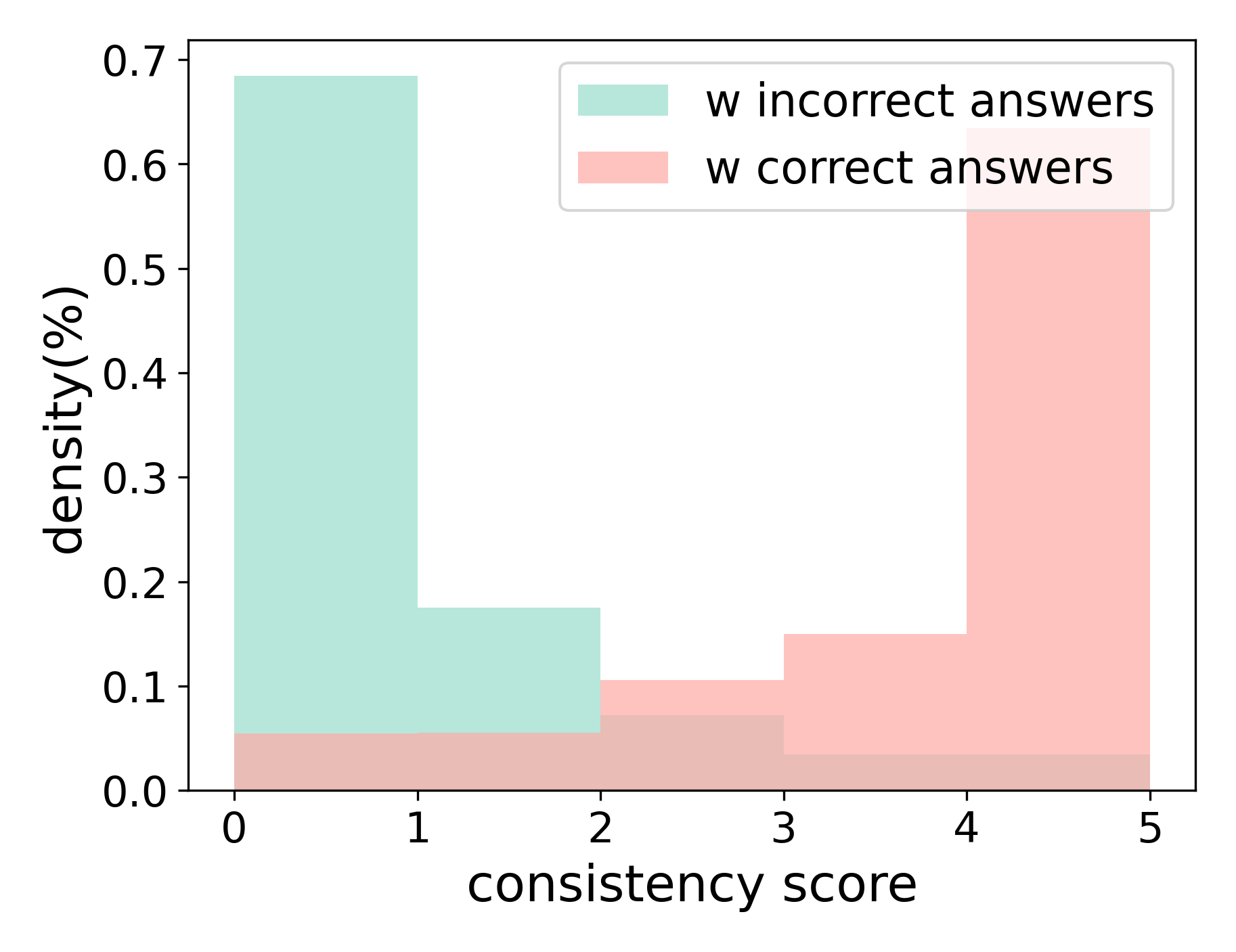
Our method identifies tokens that more reliably correlate with correct LLM reasoning, as demonstrated by increased rollout correctness (<span class="katex-eq" data-katex-display="false"> \pm 5\% </span> and <span class="katex-eq" data-katex-display="false"> \pm 10\% </span> thresholds) and improved consistency scores, compared to randomly selected tokens.
Our method identifies tokens that more reliably correlate with correct LLM reasoning, as demonstrated by increased rollout correctness ( \pm 5\% and \pm 10\% thresholds) and improved consistency scores, compared to randomly selected tokens.

The pursuit of robust reasoning in Large Language Models necessitates a rigorous examination of internal processes. This work, focusing on Paraphrastic Probing and Consistency Verification, exemplifies a dedication to structural integrity over superficial complexity. As John von Neumann observed, “The sciences do not try to explain why something is, they hardly even try to describe it.” PPCV doesn’t seek to explain LLM fallacies, but rather to identify critical tokens and refine the reasoning path through iterative consistency checks. This focus on precise structural correction, rather than broad explanatory theories, aligns with the principle that clarity is compassion for cognition – a streamlined, verifiable process yielding more reliable inference.

What Remains?

The pursuit of reasoning in large language models inevitably encounters a paradox. Performance gains, achieved through techniques like paraphrastic probing and consistency verification, merely relocate the error – they do not extinguish it. PPCV, as presented, offers a refinement of the path, but says little of the fundamental limitations of a system deriving ‘understanding’ from statistical correlation. The critical tokens identified are symptoms, not causes.

Future work must address the implicit assumptions embedded within these models. The focus shifts from optimizing inference – making the existing system ‘better’ at its inherent trick – to constructing systems that acknowledge their own uncertainty. A model which knows what it does not know is, perhaps, a more honest starting point.

Ultimately, the field will be judged not by benchmarks attained, but by the elegance of its failures. Clarity is the minimum viable kindness. To chase perfect reasoning is to mistake the map for the territory. The cracks, after all, are where the light gets in.

Original article: https://arxiv.org/pdf/2602.11361.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

See also:

2026-02-13 17:14