Author: Denis Avetisyan
New calculations refine our understanding of pion decay and tau lepton interactions, pushing the boundaries of Standard Model tests.
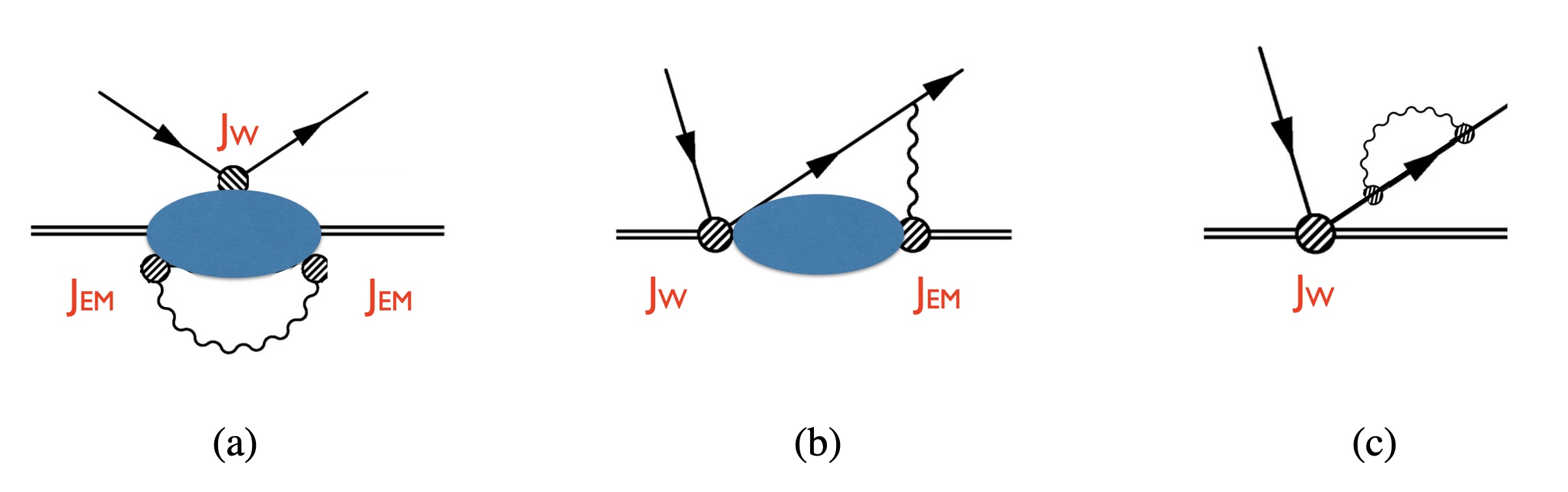
This review details advanced theoretical methods-including dispersion relations and chiral perturbation theory-to achieve high-precision determination of CKM matrix elements and constrain new physics through analyses of beta decay and τ→ππντ processes.
Precise determinations of weak decay rates are often hampered by the intricate interplay between short-distance and hadronic contributions. This Letter, ‘Pion β decay and $τ\toππν_τ$ beyond leading logarithms’, addresses this challenge through a refined analysis of charged-current processes involving pions, employing advanced techniques to consistently match these contributions and improve theoretical predictions. We demonstrate how to formulate this matching beyond leading-logarithmic accuracy, achieving a factor of three reduction in theoretical uncertainty for pion β decay and negligible uncertainty in isospin-breaking corrections to τ\toππν_τ. These advancements pave the way for more accurate determinations of the CKM matrix element V_{ud} and a precise extraction of the hadronic vacuum polarization contribution to the muon’s anomalous magnetic moment-but what further constraints on beyond-the-Standard-Model physics will these improved measurements reveal?
The Pursuit of Precision: Unveiling the Limits of Known Physics
The Standard Model of particle physics, despite its consistent success in predicting and explaining fundamental forces and particles, isn’t considered a final theory; it requires relentless scrutiny through precision tests. A key area of focus lies in determining the elements of the Cabibbo-Kobayashi-Maskawa (CKM) matrix, which describes the mixing of quarks during weak interactions. Specifically, the element V_{ud} – representing the amplitude for up quarks transforming into down quarks – demands exceptionally precise measurement. Subtle deviations from predictions based on current theoretical frameworks could unveil inconsistencies, hinting at the existence of new particles or forces beyond those described by the Standard Model, and prompting a revision of established physics. This ongoing effort necessitates increasingly sophisticated experimental techniques and theoretical calculations to push the boundaries of accuracy and probe the very foundations of particle physics.
Contemporary particle physics experiments are increasingly challenged by the inherent limitations of both experimental precision and theoretical calculations. Achieving even marginal improvements in measurements necessitates innovative techniques, such as advanced detector technologies and refined data analysis methods, to minimize systematic uncertainties. Simultaneously, theoretical predictions require increasingly complex calculations incorporating higher-order perturbative corrections and non-perturbative effects – a computationally intensive undertaking. This convergence towards the boundaries of accuracy isn’t merely a technical hurdle; it represents a crucial juncture. Any deviation from the Standard Model’s predictions, however slight, could only be revealed through these meticulously refined measurements and calculations, thereby demanding a sustained push for more sophisticated methodologies in both experimental and theoretical realms to fully explore the landscape beyond current understanding.
The relentless pursuit of precision in particle physics isn’t merely about confirming existing theories; it’s a dedicated search for the unexpected. Even minute deviations from the predictions of the Standard Model, no matter how statistically insignificant they initially appear, possess the potential to unlock entirely new realms of physics. These discrepancies act as signposts, hinting at the existence of particles or forces beyond those currently known, and prompting theorists to refine existing models or construct entirely new frameworks. This drive for deeper theoretical understanding isn’t simply academic; it’s a crucial step in resolving inconsistencies and constructing a more complete and accurate picture of the universe, potentially revealing solutions to long-standing mysteries like dark matter and the matter-antimatter asymmetry.
The quest to precisely measure the V_{ud} element of the Cabibbo-Kobayashi-Maskawa (CKM) matrix is central to validating the Standard Model and searching for physics beyond it. This parameter combination is crucial because the CKM matrix must satisfy unitarity, meaning the sum of the probabilities of all possible quark mixing events must equal one. Any deviation from unitarity, however minute, would strongly suggest the existence of new particles or interactions not currently accounted for in the Standard Model. Current experiments, utilizing techniques like beta decay and pion decay measurements, are pushing the boundaries of precision to rigorously test this fundamental principle, with even seemingly insignificant discrepancies potentially unlocking profound insights into the nature of reality and hinting at the presence of new forces or undiscovered particles influencing quark mixing.
Theoretical Impediments: The Challenge of Radiative Corrections
Precise determination of the V_{ud} Cabibbo-Kobayashi-Maskawa (CKM) matrix element necessitates the inclusion of radiative corrections. These corrections arise from quantum loop effects involving virtual particles and modify the leading-order predictions for decay rates. The calculation of radiative corrections is complicated by the fact that their precise form is often dependent on the underlying theoretical model used to describe the strong and electroweak interactions. Furthermore, the integrals involved in calculating loop diagrams are frequently divergent and require regularization and renormalization procedures, introducing scheme dependence into the final result. This model and scheme dependence contributes significantly to the theoretical uncertainty in the extracted V_{ud} value, and necessitates careful consideration when comparing theoretical predictions with experimental measurements.
Effective Field Theory (EFT) provides a systematic method for calculating radiative corrections in weak decay processes by separating physics at different energy scales. This approach involves constructing an expansion in powers of q/Λ , where q represents the momentum transfer and Λ is a characteristic scale of new physics. The Lagrangian is parameterized by a set of low-energy constants (LECs) that encapsulate the effects of high-energy degrees of freedom. The Low-Energy Effective Field Theory (LEFT) framework is a specific implementation of this strategy, tailored for nuclear beta decay and providing a consistent renormalization scheme. By including higher-order operators in the EFT expansion and accurately determining the LECs through experimental data or matching to a more complete theory, the accuracy of radiative correction calculations can be substantially improved, offering a path towards more reliable predictions for quantities like the Cabibbo-Kobayashi-Maskawa (CKM) matrix element V_{ud}.
Perturbative calculations in quantum field theory, while providing approximations to physical quantities, are inherently susceptible to scheme dependence. This arises because the renormalization procedure, used to remove infinities and define physical parameters, involves arbitrary choices of renormalization scales and definitions. Different renormalization schemes-such as minimal subtraction (\overline{MS}) or on-shell schemes-yield different intermediate results, although physical observables should be independent of the chosen scheme. However, the truncation of the perturbative series at a finite order introduces scheme-dependent ambiguities, and the resulting theoretical predictions will vary accordingly. Assessing the magnitude of this scheme dependence is crucial for quantifying the reliability of the perturbative expansion and accurately estimating theoretical uncertainties.
Recent theoretical developments have enabled the calculation of radiative corrections to Next-to-Leading Logarithmic (NLL) accuracy for processes relevant to the determination of the Unitarity Triangle parameter V_{us}V_{ud}. Prior calculations were limited to lower orders of approximation, introducing substantial theoretical uncertainty. Achieving NLL accuracy involves considering higher-order perturbative contributions, demanding computationally intensive calculations and careful renormalization procedures. This advancement has resulted in a quantified reduction of the theoretical uncertainty associated with V_{us}V_{ud} by a factor of five, representing a significant improvement in the precision of Standard Model parameter measurements and constraints on new physics.
Beyond Perturbation: Charting a Course Through Non-Perturbative Realms
Theoretical predictions in quantum field theory often rely on perturbative calculations, which can become inaccurate when dealing with strong coupling regimes. Calculating non-perturbative matrix elements – quantities representing the probability amplitudes of transitions between states that cannot be reliably computed via perturbation theory – is therefore critical for improving predictive power. These matrix elements define the parameters governing non-perturbative phenomena such as hadron masses, decay constants, and form factors. Accurately determining these values necessitates methods beyond standard perturbation theory, including Lattice QCD simulations and effective field theory approaches like Chiral Perturbation Theory, which utilize non-perturbative techniques to constrain theoretical uncertainties and refine calculations of observable quantities.
Lattice Quantum Chromodynamics (Lattice QCD) discretizes spacetime into a four-dimensional lattice, enabling numerical solutions to the theory’s equations. This approach provides a first-principles method for calculating non-perturbative quantities, such as hadron masses and decay constants, which are inaccessible via traditional perturbative methods. However, achieving statistically significant results necessitates simulations with a large number of lattice points and gauge configurations – typically on the order of 10^3 - 10^4 – coupled with computationally expensive fermion inversions at each lattice site. Consequently, Lattice QCD calculations demand substantial computational resources, including access to high-performance computing clusters and significant processing time, often measured in months or years for complex calculations.
Chiral Perturbation Theory (ChPT) is an effective field theory that provides a systematic framework for analyzing low-energy Quantum Chromodynamics (QCD). It is based on the approximate chiral symmetry of QCD, which arises due to the light masses of up, down, and strange quarks. ChPT expresses hadronic interactions as an expansion in terms of quark and gluon fields, and more specifically, in powers of momentum divided by a chiral symmetry breaking scale – typically around 1 GeV. The leading order terms involve derivatives of pion fields, reflecting the dominant role of pions as Goldstone bosons. Higher-order terms include increasingly complex interactions and additional parameters, known as low-energy constants, which encapsulate the non-perturbative aspects of QCD and require determination from experimental data or lattice QCD calculations. \mathcal{L}_{eff} = \mathcal{L}_2 + \mathcal{L}_4 + ... , where \mathcal{L}_2 represents the leading order Lagrangian with two derivatives, and subsequent terms represent higher-order corrections.
Chiral Perturbation Theory (ChPT), the effective field theory of QCD at low energies, is parameterized by a set of low-energy constants (LECs) which quantify the strength of various interactions. Accurate determination of these LECs is vital for predictive power; while they can be related to observables through experimental data, many remain poorly constrained. Lattice QCD calculations provide a complementary approach, offering first-principles determinations of hadronic properties and, crucially, constraining the values of these LECs. By matching Lattice QCD results to ChPT predictions, the LECs can be fixed with reduced systematic uncertainty, improving the reliability of low-energy predictions for hadronic processes and properties that are inaccessible to direct experimental measurement.
Constraining the CKM Matrix: A Symphony of Decay Channels
The determination of the Cabibbo-Kobayashi-Maskawa (CKM) matrix element V_{ud} relies on precise measurements from a variety of decay processes, each offering a unique perspective on this fundamental parameter. Neutron decay, for instance, provides a direct measurement sensitive to the relative strength of weak interactions affecting neutrons. Complementary information arises from pion and muon decays, where the analysis of decay products allows for independent constraints on V_{ud}. Furthermore, tau decay, though more complex, offers a valuable cross-check due to its heavier mass and different decay channels. By combining the results from these diverse decay modes – neutron, pion, beta, and tau – physicists can significantly reduce systematic uncertainties and achieve a more robust and precise determination of this crucial element of the CKM matrix, strengthening tests of the Standard Model’s consistency.
The determination of the Cabibbo-Kobayashi-Maskawa (CKM) matrix, a fundamental parameter in the Standard Model describing quark mixing, benefits significantly from a multi-faceted approach. Individual measurements of V_{ud} derived from neutron decay, pion decay, beta decay, and tau decay each possess unique strengths and weaknesses. By combining the results from these complementary decay channels, systematic uncertainties inherent to any single measurement are effectively reduced, leading to a more robust and precise extraction of the V_{ud} element. This synergistic approach doesn’t simply average values; it leverages the differing sensitivities to hadronic effects and theoretical assumptions present in each channel, offering a powerful cross-check on the underlying physics and ultimately bolstering confidence in the determined value of this crucial matrix element.
The determination of fundamental parameters like elements of the Cabibbo-Kobayashi-Maskawa (CKM) matrix relies heavily on theoretical calculations, which are often sensitive to the specific renormalization scheme employed. Renormalization Group (RG) resummation offers a powerful technique to mitigate this scheme dependence, effectively organizing perturbative calculations in terms of physically meaningful, scheme-independent quantities. By systematically including large logarithmic contributions that arise from short-distance effects, RG resummation allows for a more stable and reliable extraction of the V_{ud} matrix element. This process doesn’t simply yield a numerical value; it establishes a firmer theoretical foundation for comparing experimental measurements with Standard Model predictions, ultimately enhancing the precision and robustness of tests probing the fundamental symmetries of particle physics.
Recent analyses of hadronic vacuum polarization (HVP), a significant contributor to the anomalous magnetic moment of the muon a_μ, have achieved a notable reduction in theoretical uncertainties. By meticulously calculating the scale dependence of short-distance corrections to Next-to-Leading Logarithmic (NLL) order, researchers have refined the precision of the HVP contribution. This improvement is crucial because discrepancies between the Standard Model prediction and experimental measurements of a_μ hint at potential new physics. A more precise theoretical understanding of the HVP allows for more stringent tests of the Standard Model and facilitates the search for deviations that could signal the presence of yet undiscovered particles or interactions, ultimately pushing the boundaries of particle physics.
The pursuit of precision in particle physics, as demonstrated in this analysis of pion and tau decay, often leads to unexpectedly intricate calculations. They called it a framework to hide the panic, a common refrain when confronting the hadronic vacuum polarization and radiative corrections necessary to accurately determine the CKM matrix. It recalls Aristotle’s observation that “the ultimate value of life depends upon awareness and the power of contemplation rather than upon mere survival.” This work doesn’t merely seek survival-a functional calculation-but a deeper understanding of the fundamental forces at play, refining the theoretical landscape with each meticulously calculated correction.
The Road Ahead
The pursuit of precision, as this work demonstrates, inevitably reveals the contours of what remains unknown. Having refined the calculation of beta decay via a rigorous accounting of radiative corrections, the true limitation is not numerical but conceptual. The CKM matrix element, while increasingly well-defined, serves only as a fixed point against which deviations – whispers of new physics – might be detected. The search, therefore, shifts from parameter extraction to anomaly detection; from building the model to breaking it.
Future progress necessitates a deeper interrogation of the hadronic vacuum polarization, a term stubbornly resistant to purely theoretical calculation. The reliance on experimental input, while pragmatic, introduces a circularity. A truly elegant solution will demand a framework capable of predicting hadronic contributions ab initio, not merely parameterizing ignorance. This necessitates embracing the inherent complexity of strong interactions, but with the discipline to discard all ornamentation.
Ultimately, the value of such calculations lies not in their intrinsic accuracy, but in their capacity to expose the fragility of established theories. The Standard Model, however robust, is not a fortress, but a carefully constructed sandcastle. Each precise measurement is a wave, eroding the foundations, revealing the shoreline of undiscovered phenomena. The task is not to reinforce the walls, but to watch them fall.
Original article: https://arxiv.org/pdf/2602.11253.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- How to Build Muscle in Half Sword
- One Piece Chapter 1174 Preview: Luffy And Loki Vs Imu
- Epic Pokemon Creations in Spore That Will Blow Your Mind!
- Top 8 UFC 5 Perks Every Fighter Should Use
- All Pistols in Battlefield 6
- How to Play REANIMAL Co-Op With Friend’s Pass (Local & Online Crossplay)
- Gears of War: E-Day Returning Weapon Wish List
- Bitcoin Frenzy: The Presales That Will Make You Richer Than Your Ex’s New Partner! 💸
- How To Get Axe, Chop Grass & Dry Grass Chunk In Grounded 2
- Bitcoin’s Big Oopsie: Is It Time to Panic Sell? 🚨💸
2026-02-14 04:57