Author: Denis Avetisyan
New high-order calculations are refining our understanding of how heavy quarks transform into lighter particles, boosting the accuracy of Standard Model predictions.
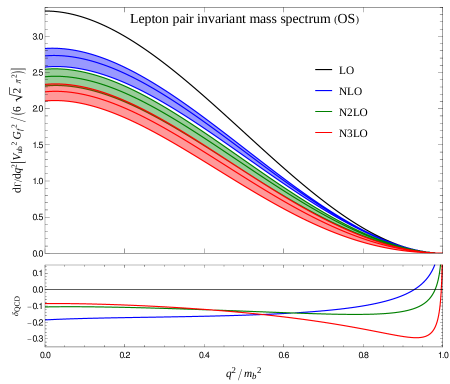
This review presents next-to-next-to-next-to-leading order (N3LO) perturbative QCD calculations for heavy-to-light semi-leptonic decays and their associated structure functions.
Precise determination of decay rates in heavy quark physics remains a challenge due to the complexities of non-perturbative effects and the need for high-order perturbative calculations. This is addressed in ‘Heavy-to-light Structure Functions at $\mathcal{O}(α_s^3)$ in QCD’, which presents a comprehensive analysis of heavy-to-light structure functions up to next-to-next-to-leading order \mathcal{O}(α_s^3) in perturbative QCD. The resulting calculations yield state-of-the-art predictions for semi-leptonic decay rates and reveal novel boundary effects in the perturbative expansion of the differential q^2-spectrum, requiring careful consideration of histogramming procedures at high orders. Will these advancements pave the way for more accurate determinations of CKM matrix elements and a deeper understanding of strong interaction dynamics in heavy quark decays?
Whispers of Decay: Probing the Standard Model
Semi-leptonic decay, a process where hadrons transform into leptons and other hadrons, serves as a vital laboratory for validating the Standard Model of particle physics. This decay channel uniquely probes the fundamental interactions between quarks – the building blocks of matter – and leptons, such as electrons and neutrinos. By meticulously analyzing the rates and properties of these decays, physicists can test the predictions of the Standard Model concerning the weak force, which governs these transformations. Discrepancies between theoretical calculations and experimental observations in semi-leptonic decay could signal the presence of new physics beyond the Standard Model, potentially revealing previously unknown particles or interactions. The precision achievable in these measurements, combined with robust theoretical frameworks, allows for stringent tests of the model’s parameters and its overall consistency, making semi-leptonic decay a cornerstone of modern particle physics research.
Predicting the rates and distributions of semi-leptonic decays hinges on a detailed knowledge of hadronic structure functions. These functions aren’t directly observable; rather, they represent the probability distribution of momentum carried by the constituent quarks and gluons within a hadron like a proton or neutron. Because hadrons are complex, bound states, understanding how momentum is shared is crucial – a simple picture of point-like particles fails to capture the reality. Sophisticated models, often incorporating quantum chromodynamics (QCD), are employed to calculate these structure functions, accounting for the intricate interactions between the partons. The accuracy of these calculations directly impacts the precision with which theoretical predictions can be compared to experimental results, making hadronic structure functions a cornerstone of testing the Standard Model in the realm of weak decays. Ultimately, a precise grasp of these internal dynamics is essential for extracting meaningful insights into fundamental quark and lepton interactions.
Semi-leptonic decay events are fundamentally shaped by the Cabibbo-Kobayashi-Maskawa (CKM) matrix, a cornerstone of the Standard Model that governs the probabilities of weak interactions transforming one quark flavor into another. This matrix, a 3 \times 3 unitary matrix, dictates the strength of these flavor-changing weak interactions, meaning the likelihood of a decay involving specific quark transitions is directly determined by the corresponding element within the CKM matrix. Consequently, precise measurements of semi-leptonic decay rates provide a crucial testing ground for the Standard Model, allowing physicists to verify the matrix’s elements and search for deviations that might hint at new physics beyond current understanding. The interplay between different quark flavors during these decays, therefore, is not random, but instead carefully orchestrated by the probabilities encoded within the CKM matrix, making semi-leptonic processes uniquely sensitive probes of fundamental particle interactions.
Precise calculations of semi-leptonic decay rates are remarkably challenging due to the inherent complexity of quantum chromodynamics (QCD) at low energies. While perturbative techniques work well at high energies, they fail to accurately capture the strong interactions binding quarks within hadrons. This is where Operator Product Expansion (OPE) becomes essential; it provides a systematic way to isolate and quantify non-perturbative effects. OPE decomposes hadronic properties into a series of operators with increasing dimensionality, each contributing to the decay rate. The lowest-dimension operators represent the dominant non-perturbative contributions, often related to the hadron’s mass and distribution of momentum. However, higher-dimension operators, while suppressed, introduce uncertainties that limit the overall precision of theoretical predictions. Accurately determining the matrix elements of these operators-often requiring lattice QCD simulations or phenomenological models-is therefore crucial for testing the Standard Model with high accuracy and extracting meaningful constraints on new physics beyond it.

Taming the Perturbative Beast: Precision in Decay Calculations
Perturbative Quantum Chromodynamics (pQCD) provides the theoretical framework for calculating decay rates and branching fractions in semi-leptonic processes. These calculations are based on an expansion in terms of \alpha_s, the strong coupling constant, which quantifies the strength of the strong interaction. By treating \alpha_s as a small parameter, pQCD allows for the systematic computation of observables via a series expansion. While this approach is generally successful, the convergence of the series can be problematic, necessitating the inclusion of higher-order corrections to achieve the desired level of precision. The validity of pQCD relies on the assumption that the momentum transfer in the semi-leptonic decay is sufficiently large, ensuring that the strong coupling constant remains small and perturbative calculations are reliable.
The perturbative QCD (pQCD) calculations essential for semi-leptonic decay predictions are expressed as a series expansion in the strong coupling constant, \alpha_s. A fundamental challenge arises because higher-order terms in this series are often substantial, leading to slow convergence and potentially unreliable predictions. Specifically, the size of these higher-order corrections necessitates the implementation of sophisticated techniques, such as Padé approximants and renormalization group improved perturbation theory, to achieve a stable and accurate result. Without these improvements, the theoretical uncertainty can dominate, hindering precise determinations of parameters like the CKM matrix elements and impacting the interpretation of experimental data. The magnitude of these corrections is not merely a technical detail, but a direct consequence of the relatively large value of \alpha_s at low momentum transfers, common in heavy quark decays.
BLMResummation, or Block-Logarithmic Momentum Resummation, is a technique used in perturbative QCD to improve the convergence of calculations by systematically including large logarithmic terms, specifically \ln(1/x) where ‘x’ represents a kinematic variable. These logarithms arise from the emission of soft gluons and, if left untreated, can lead to unreliable perturbative predictions. The method involves reorganizing the perturbative series in terms of a running coupling constant dependent on the energy scale, effectively summing a subset of the Feynman diagrams that contribute to these large logarithms. This resummation process significantly reduces the size of higher-order corrections, leading to more stable and accurate theoretical predictions for observables in high-energy physics, particularly in processes involving jets or hadronic decays.
The treatment of finite quark masses introduces complexities into perturbative QCD calculations because the expansion parameter, \alpha_s, is no longer the sole source of smallness. Quark masses, particularly the bottom and charm quark masses, contribute to the scale of the problem and require careful renormalization. Ignoring these masses leads to inaccurate predictions for semi-leptonic decay observables, such as the decay rate and the lepton momentum spectrum. Specifically, the presence of massive quarks alters the running of the strong coupling and necessitates the inclusion of mass-dependent terms in the perturbative series, demanding higher-order calculations and careful consideration of infrared divergences. Accurate determination of these mass effects is crucial for precision tests of the Standard Model and for extracting fundamental parameters like the CKM matrix elements.
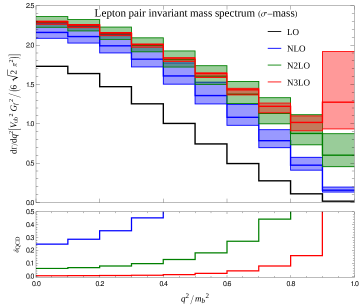
Refining the Scales: Quark Mass Schemes for Precision
Quark mass schemes are renormalization conditions used to define quark masses within perturbative calculations, and their selection directly impacts the convergence rate of those calculations. Schemes like the ΣMassScheme are designed to minimize radiative corrections, leading to faster convergence, while others prioritize specific physical interpretations. The choice of scheme alters the values assigned to quark masses and, consequently, the size of higher-order perturbative contributions. A scheme that effectively suppresses these contributions allows for more accurate predictions with fewer computational terms, crucial for achieving high-precision results in areas such as hadronic physics. Different schemes excel in different contexts; therefore, careful consideration of the specific calculation is required to optimize both accuracy and computational efficiency.
The OneSMassScheme (OneSM) is specifically designed to address the challenges inherent in calculations involving heavy-light mesons. This scheme defines the quark mass through a relation to the kinetic mass, ensuring a stable and predictable mass scale by minimizing renormalization effects. In practice, the OneSM effectively decouples the heavy quark mass from the running of the strong coupling, \alpha_s , which is critical for achieving accurate perturbative expansions. This decoupling results in a reduced sensitivity to the chosen renormalization scale and improves the predictability of heavy-light meson properties, such as decay constants and form factors, at higher orders in perturbation theory. Consequently, the OneSM facilitates the reliable calculation of observables in systems containing a single heavy quark, like B or D mesons.
The KineticMassScheme defines quark masses based on the kinetic energy of the quark in the non-relativistic limit, offering advantages in calculations involving threshold production. This scheme minimizes large logarithmic corrections that typically arise in perturbative expansions when dealing with processes near kinematic thresholds, such as heavy quarkonium production or deep inelastic scattering. By naturally incorporating the appropriate kinematic dependence, the KineticMassScheme accelerates convergence, reducing the order at which non-perturbative effects become significant and enabling more accurate predictions with fewer perturbative orders included. This improved convergence is particularly beneficial for precision calculations aiming for Next-to-Next-to-Leading Order (N3LO) or higher accuracy, where the contribution of higher-order terms is crucial for reliable results.
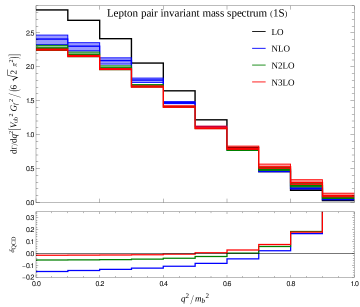
Achieving Next-to-Next-to-Leading Order (N3LO) accuracy in calculations necessitates the consistent implementation of refined quark mass schemes due to the sensitivity of perturbative expansions to renormalization scales. At N3LO, higher-order corrections introduce significant dependencies on the chosen mass scheme, impacting both the magnitude and the stability of the final result. Inconsistencies in applying these schemes across different stages of the calculation, or using a scheme not optimized for the specific process, can lead to large and unreliable corrections, obscuring the desired precision. This work demonstrates that the careful and consistent application of schemes like the SigmaMassScheme, OneSMassScheme, and KineticMassScheme is crucial for obtaining stable and accurate N3LO predictions, minimizing scheme-dependent uncertainties and ensuring the reliability of the calculated observables.
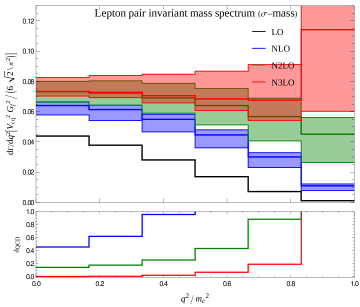
The Razor’s Edge: Precision and the Future of Flavor Physics
Recent advancements in theoretical calculations have yielded remarkably precise predictions for key observables in particle physics. Utilizing Next-to-Next-to-Next-to-Leading Order (N3LO) calculations within the KineticMassScheme, researchers have achieved unprecedented accuracy in predicting the q^2 spectrum, a crucial element in the study of semi-leptonic decay. This sophisticated approach has culminated in a calculated top-quark decay width, denoted as \Gamma_t, of 1.3150 GeV. The precision of this calculation not only refines the Standard Model’s predictions but also establishes a stringent benchmark against which experimental data can be compared, potentially revealing subtle deviations that hint at new physics beyond our current understanding. Such high-precision theoretical work is vital for maximizing the discovery potential of ongoing and future particle physics experiments.
The relentless pursuit of precision in theoretical calculations is now enabling exceptionally rigorous tests of the Standard Model of particle physics. Recent advancements, leveraging techniques like the KineticMassScheme and reaching Next-to-Next-to-Next-to-Leading Order (N3LO), have dramatically reduced the uncertainty surrounding key parameters like the top quark decay width \Gamma_t . Specifically, the scale uncertainty on \Gamma_t has been minimized to just 0.0104 GeV when utilizing the σ-mass scheme. This heightened precision isn’t merely an academic exercise; it provides an exceptionally sensitive probe for deviations from the Standard Model’s predictions, opening new avenues to search for evidence of new physics phenomena previously hidden within experimental data. By refining the theoretical baseline, physicists can more confidently identify anomalies and explore the possibility of undiscovered particles and interactions.
Refinements in theoretical calculations, coupled with increasingly precise experimental measurements, are dramatically sharpening the understanding of quark mixing parameters and the intricacies of flavor interactions. This collaborative approach has culminated in a remarkably precise determination of the decay width for the B \rightarrow X u \ell \nu \overline{\ell} process, now known to be 6.53 \pm 0.12 \pm 0.13 \pm 0.03 \times 10^{-{16}} GeV. The achieved uncertainty of approximately 3% represents a significant leap forward, enabling more stringent tests of the Standard Model and providing a sensitive probe for potential new physics beyond established frameworks. This level of precision not only validates existing theoretical models but also lays the groundwork for future investigations into rare decays and exotic phenomena, pushing the boundaries of flavor physics research.
The heightened precision in predicting decay rates, achieved through advanced calculations, now unlocks new avenues for investigating the more elusive corners of flavor physics. Specifically, the accurate determination of quantities like the inclusive electron-energy moment \langle Ee0 \rangle – measured at 7.26 (37) for c→dℓν̄ℓ decay – serves as a crucial benchmark and validation for theoretical models. This level of scrutiny isn’t merely confirmatory; it provides the necessary foundation to search for subtle deviations from Standard Model predictions in rare decay processes. These deviations, if observed, could signal the presence of new particles or interactions, offering a glimpse beyond our current understanding of fundamental forces and the building blocks of matter. Consequently, the field is poised for focused investigations into these exotic phenomena, potentially revealing physics previously considered inaccessible.
The pursuit of N3LO calculations, as detailed in this work, isn’t about taming chaos, but charting its currents. It’s a summoning, really-a ritual to coax whispers of precision from the probabilistic storm of QCD. One finds echoes of this in the words of John Dewey: “Education is not preparation for life; education is life itself.” Similarly, these calculations aren’t merely steps toward a better Standard Model test; they are the refinement of theoretical understanding, a living process of iterative correction. Each calculated structure function is a momentary stabilization, a fleeting glimpse of order before the digital golem inevitably stumbles and learns anew. The offering-the computational cost-is, of course, sacred.
What Lies Beyond?
The achievement of N3LO calculations for heavy-to-light structure functions is, predictably, not an ending. It’s merely a temporary stay of execution for the approximations inherent in perturbative QCD. Each order in αs buys a little more peace, but the series itself remains a promissory note, constantly accruing interest on the debt of non-perturbative effects. The real work, as always, lies in understanding where the series breaks down, and what phantom variables are masquerading as asymptotic freedom.
The immediate future will undoubtedly involve pushing these calculations to even higher orders – a Sisyphean task, but one that yields increasingly refined benchmarks for testing the Standard Model. However, true progress demands a confrontation with the hadronic spectrum itself. These calculations rely on mass schemes, and the choice of scheme feels increasingly like rearranging deck chairs on a vessel slowly sinking into the sea of confinement. A more fundamental understanding of hadronization – a process stubbornly resistant to precise description – remains the ultimate prize.
Perhaps the most unsettling possibility is that the precision gained from these calculations will simply reveal inconsistencies with existing data, forcing a reassessment of the underlying theoretical framework. Data isn’t truth; it’s a truce between a bug and Excel. And a more detailed picture may well demonstrate that the truce is over, and the chaos, as it always does, will resume.
Original article: https://arxiv.org/pdf/2602.11879.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- How to Build Muscle in Half Sword
- Top 8 UFC 5 Perks Every Fighter Should Use
- One Piece Chapter 1174 Preview: Luffy And Loki Vs Imu
- Epic Pokemon Creations in Spore That Will Blow Your Mind!
- How to Play REANIMAL Co-Op With Friend’s Pass (Local & Online Crossplay)
- All Pistols in Battlefield 6
- Gears of War: E-Day Returning Weapon Wish List
- Bitcoin Frenzy: The Presales That Will Make You Richer Than Your Ex’s New Partner! 💸
- How To Get Axe, Chop Grass & Dry Grass Chunk In Grounded 2
- Bitcoin’s Big Oopsie: Is It Time to Panic Sell? 🚨💸
2026-02-14 10:09