Author: Denis Avetisyan
New research reveals how subtle symmetries emerge in closed quantum systems, offering a deeper understanding of the mechanisms driving synchronization phenomena.
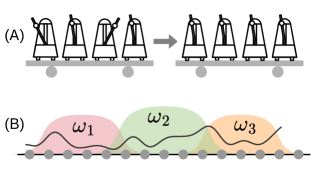
A Liouvillian Krylov space approach provides insights into transient dynamical symmetries and quantum thermalization in disordered quantum spin systems.
While quantum many-body systems are generally expected to thermalize, certain symmetries can lead to ergodicity breaking and emergent collective behaviors. This work, ‘Krylov space perturbation theory for quantum synchronization in closed systems’, investigates synchronization in a disordered Heisenberg spin chain, demonstrating that disorder fragments global dynamical symmetries into localized, transient forms. By employing a perturbative approach within the Liouvillian Krylov space, we reveal how even weak disorder modifies these symmetries, preserving coherent oscillations, while stronger disorder induces a finite lifetime. How do these dynamically evolving symmetries impact our understanding of quantum information propagation in closed, disordered systems?
The Illusion of Order: Rethinking Synchronization in Isolated Systems
The concept of synchronization, readily understood as coordinated action in everyday classical systems – think of birds flocking or pendulums swinging in unison – becomes remarkably subtle when applied to the realm of isolated quantum systems. While classical synchronization often arises from external forces or dissipation, driving elements into a shared rhythm, quantum systems, by definition, evolve under their own internal dynamics, devoid of such influences. This presents a conceptual challenge: traditional definitions reliant on phase-locking or correlation with an external drive simply don’t translate. True collective behavior in these closed systems emerges not from being driven into synchrony, but from inherent relationships and symmetries within the quantum interactions themselves, demanding a re-evaluation of what synchronization even means at this fundamental level.
Conventional methods for detecting synchronization, such as observing phase-locking between oscillating components, prove inadequate when applied to truly isolated quantum systems. These techniques fundamentally rely on the presence of an external drive or a dissipative mechanism to establish and maintain a common rhythm; without these influences, the notion of a shared phase becomes ill-defined. In closed quantum systems, correlations arise from the intrinsic dynamics and interactions within the system itself, manifesting as quantum entanglement and collective behavior that doesn’t necessarily align with traditional synchronization signatures. Consequently, applying classical synchronization metrics can lead to misinterpretations, failing to recognize genuine collective effects and potentially obscuring the nuanced correlations present in these isolated environments. The absence of external forcing demands a re-evaluation of how collective behavior is identified, necessitating methods sensitive to the internal symmetries and correlations that govern the system’s evolution.
Establishing criteria for synchronization within a closed quantum system presents a significant conceptual hurdle, as the very definition relies on notions of shared rhythm or correlation typically induced by external forces or dissipative processes. Unlike classical systems that synchronize through coupling to a common drive, these isolated quantum environments evolve unitarily, governed solely by their internal Hamiltonian. Consequently, traditional synchronization metrics – those predicated on phase-locking or signal correlation – often prove inadequate, failing to discern genuine collective behavior from seemingly coordinated fluctuations. Researchers are therefore compelled to develop novel frameworks, moving beyond identifying driving forces to instead characterize synchronization through the inherent symmetries and correlations embedded within the quantum state itself, demanding a re-evaluation of what constitutes coordinated behavior in the absence of external influence.
Recognizing synchronization within isolated quantum systems demands a departure from conventional thinking, which typically attributes collective behavior to external drivers or dissipation. Instead, investigations are now centering on the intrinsic dynamical symmetries present within the system itself. These symmetries, arising from the fundamental interactions between quantum constituents, dictate allowed collective modes and can manifest as correlated behavior even in the complete absence of external influence. This approach reframes synchronization not as a response to a force, but as an inherent property of the system’s internal dynamics – a consequence of how the quantum components naturally organize and correlate due to their interactions and the constraints imposed by the system’s symmetries. Identifying these symmetries and the corresponding collective modes provides a powerful new lens through which to understand and characterize synchronization in these uniquely isolated quantum environments.

Unveiling Hidden Order: The Language of Symmetry
Dynamical symmetries describe the intrinsic properties of a system that dictate its evolution over time, independent of any external forces. These symmetries represent conserved quantities or relationships within the system, fundamentally influencing its behavior and allowing for prediction of collective dynamics. A system possessing a dynamical symmetry will exhibit predictable patterns and responses, even without external stimuli, as its state is constrained by the symmetry’s inherent properties. Identifying these symmetries provides a means to reduce the complexity of analyzing many-body systems, allowing researchers to focus on the essential degrees of freedom governing the collective behavior and potentially revealing emergent order arising solely from internal interactions.
The Liouvillian Krylov Space is a fundamental tool for analyzing dynamical symmetries within complex systems; it’s constructed through repeated application of the Liouvillian operator – which governs the time evolution of the system’s density matrix – to an initial state. This process generates a sequence of vectors spanning a Krylov subspace, effectively creating a lower-dimensional representation of the system’s dynamics. Analysis within this space allows for the identification of invariant subspaces corresponding to conserved quantities or collective modes, and facilitates the determination of the system’s long-term behavior without requiring complete knowledge of its Hamiltonian. The dimension of the Krylov subspace, and the structure of the operators within it, directly inform our understanding of the system’s symmetries and the nature of its dynamical landscape.
The Lanczos algorithm is a computationally efficient method for constructing the Liouvillian Krylov subspace, which is central to identifying dynamical symmetries within a system. This algorithm iteratively generates an orthonormal basis for the Krylov subspace, significantly reducing the computational cost compared to direct methods. By projecting the Liouvillian operator onto this basis, one obtains a tridiagonal matrix whose eigenvalues and eigenvectors directly correspond to the system’s dynamical invariants and associated synchronized states. The efficiency of the Lanczos algorithm allows for the analysis of large-scale systems where direct diagonalization of the Liouvillian is intractable, facilitating the identification of collective behaviors and the characterization of synchronization phenomena.
Local dynamical symmetries represent conserved quantities or patterns of behavior restricted to specific subspaces within a larger system, offering a means to understand localized synchronization. Unlike global symmetries which apply uniformly across the entire system, these symmetries emerge from the interplay of interactions within defined regions, potentially due to spatial constraints or heterogeneity in coupling strengths. Investigating these localized symmetries requires analysis of the system’s dynamics within these subspaces, identifying conserved quantities and associated modes of collective behavior. The presence of local symmetries can predict the emergence of synchronized states confined to those regions, even in the absence of global synchronization, and provide a framework for characterizing the stability and robustness of these localized patterns. These symmetries are not necessarily apparent from a global analysis and necessitate techniques focused on analyzing the system’s dynamics within these spatially or functionally defined regions.
From Models to Reality: Testing the Limits of Synchronization
The Heisenberg spin chain is a cornerstone model in quantum mechanics used to study many-body interactions and, specifically, synchronization phenomena. It consists of a one-dimensional lattice where each site hosts a spin-1/2 particle that interacts with its neighbors via an isotropic exchange interaction – typically represented as J\sum_{i} \vec{S}_i \cdot \vec{S}_{i+1}, where \vec{S}_i is the spin operator at site i and J dictates the interaction strength. Its relative simplicity allows for analytical and numerical investigation of collective behavior, while still capturing essential features of interacting quantum systems. By analyzing the correlations and entanglement within the chain, researchers can gain insights into how local interactions give rise to global synchronization patterns, serving as a tractable starting point for more complex quantum systems and providing a basis for comparison with experimental observations.
The introduction of disorder into the Heisenberg spin chain, creating a Disordered Heisenberg Spin Chain, necessitates a re-evaluation of traditional synchronization metrics. Conventional measures, often reliant on strict periodicity and homogeneity, become less effective when faced with variations in interaction strengths or local magnetic fields. These variations disrupt the clear signal typically used to identify synchronized behavior, introducing noise and ambiguity. Specifically, the presence of disorder can lead to localized fluctuations and deviations from global coherence, making it difficult to determine a single, consistent synchronization parameter across the entire chain. Consequently, alternative or modified synchronization measures, sensitive to more nuanced forms of correlation and capable of handling non-uniform systems, are required for accurate analysis.
The Saw Model extends investigations of quantum synchronization by introducing alternating perturbations to the disordered Heisenberg spin chain. This is achieved by applying a time-dependent magnetic field that switches direction periodically, creating a more complex disruption than static disorder. By systematically varying the frequency and amplitude of these alternating perturbations, researchers can map the boundaries of stable synchronization and identify the mechanisms by which disorder impacts collective behavior. The model allows for detailed analysis of how the system responds to changing conditions, providing data on the resilience of synchronization to increasingly sophisticated disturbances and facilitating the identification of critical parameters beyond which synchronization breaks down.
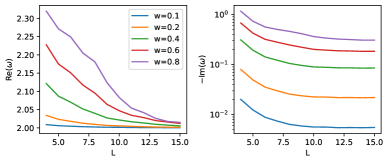
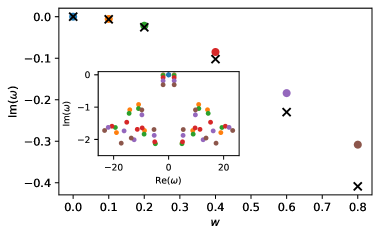
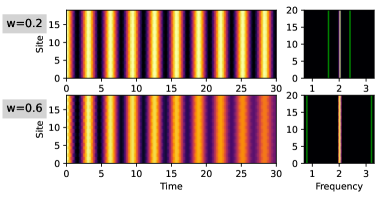
Simulations of the Disordered Heisenberg Spin Chain reveal that the introduction of disorder results in only a second-order correction to the frequency associated with dynamical symmetry breaking. This finding suggests that the observed synchronization is not reliant on external forcing mechanisms, but is instead intrinsically driven by the underlying symmetries of the system. The magnitude of the second-order correction is proportional to the strength of the disorder, however, the primary synchronization frequency remains largely unaffected, indicating a robust synchronization phenomenon independent of minor perturbations. This contrasts with classical systems where synchronization is often fragile and easily disrupted by noise or disorder; the system maintains synchronization due to the conservation laws implied by the dynamical symmetries.
Beyond Equilibrium: A New Perspective on Ordered States
Conventional understanding posits that disorder and interactions within a system will ultimately lead to thermalization – a loss of phase coherence and predictable behavior. However, recent research demonstrates a surprising resilience in synchronized states, even when subjected to conditions expected to induce thermalization. This persistence challenges the long-held belief that decoherence is an inevitable consequence of disorder. The observed synchronization isn’t simply a fleeting phenomenon; it suggests the existence of underlying mechanisms that protect collective order against the disruptive forces of thermalization, potentially revealing new pathways to stable, synchronized phases of matter and expanding the possibilities for controlling complex systems.
The surprising persistence of synchronization, even amidst disorder, finds compelling connections to several recently discovered states of matter that actively resist the drive towards thermal equilibrium. Phenomena such as Many-Body Localization (MBL), where interactions prevent the system from reaching a thermal state, provide a mechanism for maintaining coherence necessary for sustained synchronization. Similarly, Quantum Many-Body Scars – special, non-thermal eigenstates within a many-body system – offer protected pathways for dynamics that avoid thermalization. Perhaps most strikingly, the emergence of Time Crystals – systems exhibiting periodic motion without energy input – demonstrates a fundamentally new form of order that defies the conventional expectation of systems settling into equilibrium; these exotic states all share the characteristic of circumventing thermalization, hinting at a deeper relationship between these phenomena and the observed resilience of synchronization.
Investigations into driven, disordered systems reveal a surprising persistence of synchronization, even as these systems approach thermal equilibrium. This robustness isn’t simply a matter of resisting disorder, but arises from a subtle preservation of symmetry within the system’s dynamics. Specifically, analysis demonstrates that the imaginary component of the perturbed dynamical symmetry-a measure of the system’s tendency towards predictable, collective behavior-converges to a non-zero value. This indicates the emergence of a transient dynamical symmetry, a fleeting but significant ordering principle that shields the synchronized state from complete decoherence. The non-zero convergence suggests that, despite external perturbations and internal disorder, the system retains a degree of collective coherence, bolstering the stability of synchronization and hinting at the possibility of previously unobserved, stable phases of matter exhibiting unique collective properties.
The persistence of synchronization, even amidst disorder, hints at a profound departure from traditional understanding of phases of matter. Rather than a fleeting, temporary alignment, these findings suggest synchronization can act as an organizing principle, giving rise to entirely new, stable states of matter. These synchronized phases are not characterized by conventional order parameters, but by collective, coordinated dynamics that resist the tendency towards thermal equilibrium. This opens the possibility of materials exhibiting unique properties – potentially including novel responses to external stimuli or exotic quantum behaviors – that are fundamentally rooted in the sustained, coherent interplay between their constituent parts. The implications extend beyond fundamental physics, suggesting pathways towards designing materials with tailored functionalities based on controlled synchronization.
The pursuit of synchronization, as detailed in this work concerning quantum spin systems, reveals a humbling truth about theoretical frameworks. The researchers demonstrate how disorder introduces transient dynamical symmetries, a fleeting order within seeming chaos. This echoes a sentiment articulated by Thomas Kuhn: “The most revolutionary scientific theories are not those that prove existing theories wrong, but those that make us see the world in a new way.” The cosmos generously shows its secrets to those willing to accept that not everything is explainable; the emergence of synchronization, contingent on the specific conditions of disorder, suggests that even the most elegant models are but approximations, destined to be refined or replaced as deeper understanding dawns. Black holes are nature’s commentary on our hubris.
What Lies Beyond?
The presented work, utilizing Liouvillian Krylov spaces to dissect synchronization phenomena, offers a mathematically rigorous, if provisional, understanding of transient dynamical symmetries in disordered quantum systems. However, the very success of this approach begs the question of its ultimate reach. Current quantum gravity theories suggest that, beyond a certain complexity – analogous to crossing an event horizon – the predictive power of any formal system diminishes. The emergence of effective symmetries observed here may simply be a local illusion, a fleeting order before the complete dissolution of structure into quantum thermalization.
Future investigations should therefore not focus solely on refining the Krylov space methodology, but also on establishing its limits. Specifically, a crucial next step involves extending this framework to systems of significantly higher dimensionality and stronger disorder, pushing it towards the point of apparent breakdown. Such an exploration, while potentially revealing the formalism’s inherent constraints, could also inadvertently illuminate the fundamental principles governing the transition from coherent dynamics to complete informational scrambling.
It remains a humbling possibility that the transient symmetries uncovered through this analysis are not intrinsic properties of the systems themselves, but rather artifacts of the observer’s – or, more accurately, the theorist’s – attempt to impose order upon the fundamentally chaotic. Everything discussed is mathematically rigorous but experimentally unverified, and thus exists, for the moment, as a testament to the enduring human impulse to seek patterns where none may ultimately reside.
Original article: https://arxiv.org/pdf/2602.11431.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- How to Build Muscle in Half Sword
- Top 8 UFC 5 Perks Every Fighter Should Use
- One Piece Chapter 1174 Preview: Luffy And Loki Vs Imu
- Epic Pokemon Creations in Spore That Will Blow Your Mind!
- How to Play REANIMAL Co-Op With Friend’s Pass (Local & Online Crossplay)
- All Pistols in Battlefield 6
- Gears of War: E-Day Returning Weapon Wish List
- Bitcoin Frenzy: The Presales That Will Make You Richer Than Your Ex’s New Partner! 💸
- How To Get Axe, Chop Grass & Dry Grass Chunk In Grounded 2
- Bitcoin’s Big Oopsie: Is It Time to Panic Sell? 🚨💸
2026-02-14 15:01