Author: Denis Avetisyan
Researchers have achieved a first-of-its-kind lattice QCD calculation of nucleon parton distribution functions, opening a new pathway for understanding the internal structure of protons and neutrons.
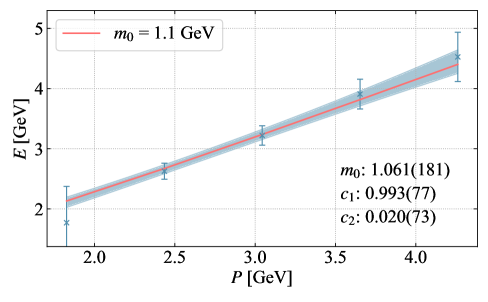
This study utilizes the Coulomb gauge within a Large Momentum Effective Theory framework to extract parton distribution functions and demonstrates consistency with existing phenomenological results.
Understanding the internal structure of nucleons remains a fundamental challenge in modern nuclear physics, complicated by the non-perturbative nature of quantum chromodynamics. This work, ‘Nucleon Parton Distribution Functions from Boosted Correlations in the Coulomb gauge’, presents a first exploratory lattice QCD calculation of nucleon parton distribution functions (PDFs) utilizing a novel approach based on boosted correlations within the Coulomb gauge, circumventing the need for traditional Wilson lines. The resulting valence-quark PDFs demonstrate good convergence with increasing momentum and align with existing phenomenological analyses for all spin structures, while discrepancies observed in the full-quark-channel PDFs suggest potential excited-state contamination. Does this Coulomb gauge method offer a computationally efficient pathway towards high-precision determination of nucleon PDFs and ultimately a more complete understanding of hadron structure?
Deconstructing Hadronic Architecture: A First-Principles Approach
The very essence of a hadron – protons, neutrons, and their more exotic cousins – lies not in being fundamental particles, but composite structures. Determining how momentum is apportioned amongst these constituent quarks and gluons represents a foundational challenge in nuclear physics. It’s not simply a matter of counting parts; the strong force dictates a complex interplay where gluons themselves carry a significant fraction of the hadron’s momentum, and quarks are constantly exchanging these force-carrying particles. Understanding this internal momentum distribution – the parton distribution function – is crucial for interpreting experimental results from particle colliders like the Large Hadron Collider, and for building accurate theoretical models of nuclear matter. Precisely mapping this distribution reveals the underlying dynamics of the strong force and provides insights into the very nature of confinement – why quarks are never observed in isolation.
The exploration of hadrons – particles like protons and neutrons – is fundamentally hampered by the nature of the strong force. Unlike electromagnetism, which weakens with distance, the strong force remains constant, even as quarks and gluons attempt to separate within a hadron. This ‘constant’ strong coupling prevents the application of standard perturbative techniques – methods that rely on approximations valid only when interactions are weak. Consequently, calculations based on these traditional approaches become unreliable and lose predictive power when dealing with the internal dynamics of hadrons. The inability to accurately model these interactions presents a significant obstacle to understanding the structure and behavior of all matter composed of these fundamental building blocks, necessitating alternative computational methods like Lattice QCD to navigate this complex regime.
Lattice Quantum Chromodynamics (QCD) presents a powerful, first-principles method for investigating the internal structure of hadrons, yet directly obtaining parton distribution functions (PDFs) from these calculations poses a significant challenge. Since lattice QCD operates on a discrete, four-dimensional spacetime grid, a direct comparison to experimentally measured PDFs-which are defined in continuous space-is impossible. Innovative techniques, therefore, are crucial; these typically involve calculating large-momentum-transfer observables, such as deeply virtual Compton scattering or proton form factors, on the lattice and then employing theoretical frameworks – often involving a process called “pseudo-PDFs” – to extrapolate these lattice results to the physical, continuous-space PDFs. This extrapolation demands careful control of discretization effects and requires sophisticated analysis to ensure reliable connections between the lattice calculations and the experimentally accessible quantities that characterize hadron structure and dynamics.
LaMET: A Rigorous Path to Parton Distribution Functions
Large Momentum Effective Theory (LaMET) offers a method for computing parton distribution functions (PDFs) directly from first-principles lattice quantum chromodynamics (QCD) calculations. This is achieved by simulating hadrons moving with large longitudinal momentum, effectively boosting the frame of reference. The presented study demonstrates the calculation of PDFs with a maximum momentum of 3.04 GeV, representing a significant advancement in bridging the gap between non-perturbative lattice QCD and the perturbative regime used in collider physics. This approach allows for a systematic calculation of PDFs without relying on phenomenological models or experimental data, providing a crucial theoretical input for high-energy physics calculations.
The Large Momentum Effective Theory (LaMET) approach necessitates the use of gauge-invariant methods, collectively termed GI_Method, to ensure the physical relevance of calculated Parton Distribution Functions (PDFs). This requirement stems from the fundamental principles of Quantum Chromodynamics (QCD), where gauge symmetry dictates that observable quantities must be independent of gauge choice. Consequently, the underlying gauge configurations used in lattice QCD calculations-such as those generated by the HotQCD_Ensemble-must be carefully considered and manipulated. Specifically, maintaining gauge invariance during the boosting process, which is central to LaMET, demands that all operators and correlation functions are constructed in a gauge-invariant manner, preventing spurious contributions from gauge degrees of freedom and ensuring accurate extraction of the desired physical quantities.
The Coulomb Gauge and Wilson Lines are integral to constructing the background fields required for LaMET calculations. The Coulomb Gauge, a specific choice of gauge fixing condition, simplifies the calculation by imposing a condition on the vector potential A_{\mu}, effectively removing unwanted degrees of freedom and ensuring a physically interpretable result. Wilson Lines, path-ordered exponential operators of the gauge field, are then employed to define the gauge-invariant connections between spatial points, accounting for the effects of the background gluon fields on the propagating quarks. These Wilson Lines act as crucial building blocks for calculating the matrix elements needed to extract parton distribution functions, ensuring the calculated PDFs are gauge-invariant and physically meaningful.
The HotQCD ensemble constitutes the finite-temperature lattice QCD configurations utilized in these PDF calculations. This ensemble is generated with N_f = 2 + 1 + 1 flavors of improved staggered quarks, incorporating up, down, strange, and charm quarks. Simulations are performed on 48^3 \times 128 lattices with a bare coupling of \beta = 7.99. The sea quark masses are tuned to achieve physical pion masses, specifically m_{\pi} \approx 135 MeV. These parameters define the statistical and systematic uncertainties inherent in the subsequent LaMET calculations, and the ensemble provides the background fields necessary for extracting momentum distributions.
Renormalization Procedures: Ensuring Quantitative Precision
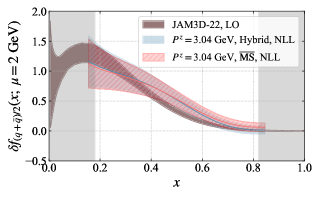
Hybrid renormalization is a non-perturbative approach to removing ultraviolet divergences encountered in lattice Quantum Chromodynamics (QCD) calculations. It combines the advantages of both direct and mixed renormalization schemes, specifically utilizing the RIMOM scheme – a condition on the quark propagator that defines renormalized parameters at a specific momentum scale. This process involves calculating bare and renormalized quantities, then iteratively solving for the renormalization constants that relate them. The RIMOM scheme is favored for its simplicity and well-defined procedure, allowing for precise determination of renormalization factors.
Leading Renormalon Resummation (LRR) addresses the issue of large logarithmic corrections, specifically those of the form \log(Q^2), which arise in perturbative calculations of parton distribution functions (PDFs). These logarithms, when unaddressed, can lead to significant inaccuracies in predictions, particularly at high energy scales (high Q^2). LRR is a technique that reorganizes the perturbative series to effectively sum these leading logarithmic terms to all orders, improving the convergence and stability of the calculation. By including LRR, the theoretical uncertainties associated with the truncation of the perturbative series are reduced, leading to more precise and reliable PDF extractions and ultimately, more accurate predictions for high-energy physics processes.
Power corrections arise in lattice QCD calculations due to the discretization of spacetime – represented by the finite lattice spacing – and the use of finite quark mass. These corrections, which scale as powers of a (lattice spacing) and 1/m (inverse quark mass), introduce systematic errors into the extracted Parton Distribution Functions (PDFs). Rigorous control requires performing calculations at multiple lattice spacings and quark masses, extrapolating to the continuum limit (a \rightarrow 0) and the physical quark mass. The Static Quark Mass provides crucial input for understanding and quantifying these power corrections, particularly those related to the heavy quark region, and is therefore integral to the reliable determination of PDFs from lattice QCD.
Mapping the Internal Dynamics of Hadrons
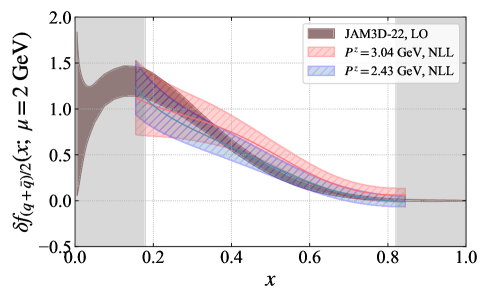
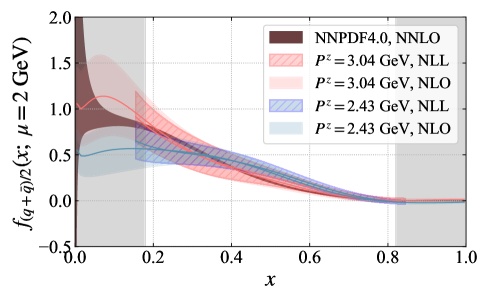
Researchers are now capable of dissecting the internal structure of hadrons – particles like protons and neutrons – by employing the LaMET framework in conjunction with carefully applied renormalization procedures. This sophisticated approach allows for the extraction of diverse parton distribution functions (PDFs), essentially revealing how momentum is shared amongst the constituent quarks and gluons. Specifically, calculations can yield Unpolarized PDFs, which describe the distribution of momentum without considering spin; Helicity PDFs, detailing the distribution of quarks and gluons aligned with the hadron’s spin; and Transversity PDFs, which probe the distribution of quarks polarized perpendicular to both the hadron’s momentum and spin. Obtaining these multiple PDF types offers a more complete and nuanced understanding of the strong force dynamics governing these fundamental particles.
Parton distribution functions (PDFs) offer a detailed snapshot of a hadron’s internal structure, revealing how its momentum is partitioned among its constituent quarks and gluons. These functions aren’t simply a matter of counting particles; instead, they describe probabilities – the likelihood of finding a particular parton carrying a specific fraction of the hadron’s total momentum. Understanding this distribution is crucial because it governs how hadrons interact in high-energy collisions, such as those at the Large Hadron Collider. A comprehensive set of PDFs, including those for unpolarized, helicity, and transverse parton states, allows physicists to precisely model these interactions and ultimately decipher the fundamental forces governing matter. The resulting picture is not static; the momentum distribution changes depending on the hadron’s energy and the specific collision process, demanding increasingly sophisticated theoretical frameworks and experimental probes to fully map this internal landscape.
Recent calculations employing the Coulomb gauge method have yielded parton distribution functions (PDFs) that exhibit strong consistency with established gauge-invariant theoretical predictions. This agreement serves as a crucial validation of the Coulomb gauge approach for determining PDFs, a technique that offers a complementary pathway to traditional methods. Furthermore, the derived PDFs demonstrate broad concordance with phenomenological determinations – those extracted from experimental data – suggesting a robust and reliable description of the internal momentum distribution within hadrons. This alignment reinforces the utility of lattice QCD calculations in providing first-principles insights into the fundamental structure of matter and offers a promising avenue for refining our understanding of strong interaction physics.
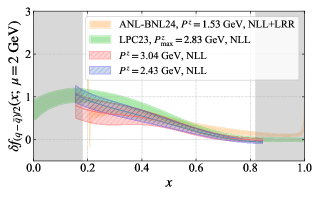
The pursuit of nucleon Parton Distribution Functions, as detailed in this study, demands a rigorous framework-one built upon demonstrably true principles. This mirrors the philosophical stance of Immanuel Kant, who famously stated, “Two things fill me with ever new and increasing admiration and awe…the starry heavens above and the moral law within.” Just as Kant sought an unwavering moral law, this research aims for unwavering mathematical consistency in defining hadron structure. The Coulomb gauge method, explored here, offers a path toward provable results, bypassing the complexities of gauge invariance while still aligning with established phenomenological data – a testament to the power of a logically sound foundation in even the most complex calculations.
Where Do We Go From Here?
The demonstrated viability of extracting nucleon parton distribution functions within a Coulomb gauge framework, while logically sound, does not resolve the fundamental tension between non-perturbative lattice calculations and the perturbative regime demanded by established phenomenological analyses. Consistency with existing results is…satisfying, certainly, but it merely confirms the method’s functionality, not its inherent superiority. The crucial question remains: does this approach reveal any genuinely new physics, or simply re-establish what is already known with a different, arguably more convoluted, computational expenditure?
Future efforts must concentrate on systematically addressing the limitations inherent in quasi-PDF methods. Specifically, rigorous control over the boosting procedure is paramount; any ambiguity in extrapolating to infinite momentum will continue to undermine the deterministic nature required for truly predictive power. Furthermore, the renormalization procedure, while functional in this instance, deserves intensified scrutiny; a robust, analytically-proven scheme is essential, not merely an empirically-tuned one.
The ultimate test lies not in replicating known results, but in predicting phenomena currently beyond experimental reach. Only then will this, or any other, approach to hadron structure move beyond elegant calculation and approach the realm of genuine understanding. The pursuit of mathematical purity, after all, is not an end in itself, but a means to arrive at an unassailable truth.
Original article: https://arxiv.org/pdf/2602.11283.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- How to Build Muscle in Half Sword
- Top 8 UFC 5 Perks Every Fighter Should Use
- One Piece Chapter 1174 Preview: Luffy And Loki Vs Imu
- Epic Pokemon Creations in Spore That Will Blow Your Mind!
- How to Play REANIMAL Co-Op With Friend’s Pass (Local & Online Crossplay)
- All Pistols in Battlefield 6
- Mewgenics Tink Guide (All Upgrades and Rewards)
- Gears of War: E-Day Returning Weapon Wish List
- Bitcoin Frenzy: The Presales That Will Make You Richer Than Your Ex’s New Partner! 💸
- How To Get Axe, Chop Grass & Dry Grass Chunk In Grounded 2
2026-02-14 18:38