Author: Denis Avetisyan
A new approach leverages path signatures to capture the nuances of temporal dynamics, improving the performance of offline reinforcement learning algorithms.
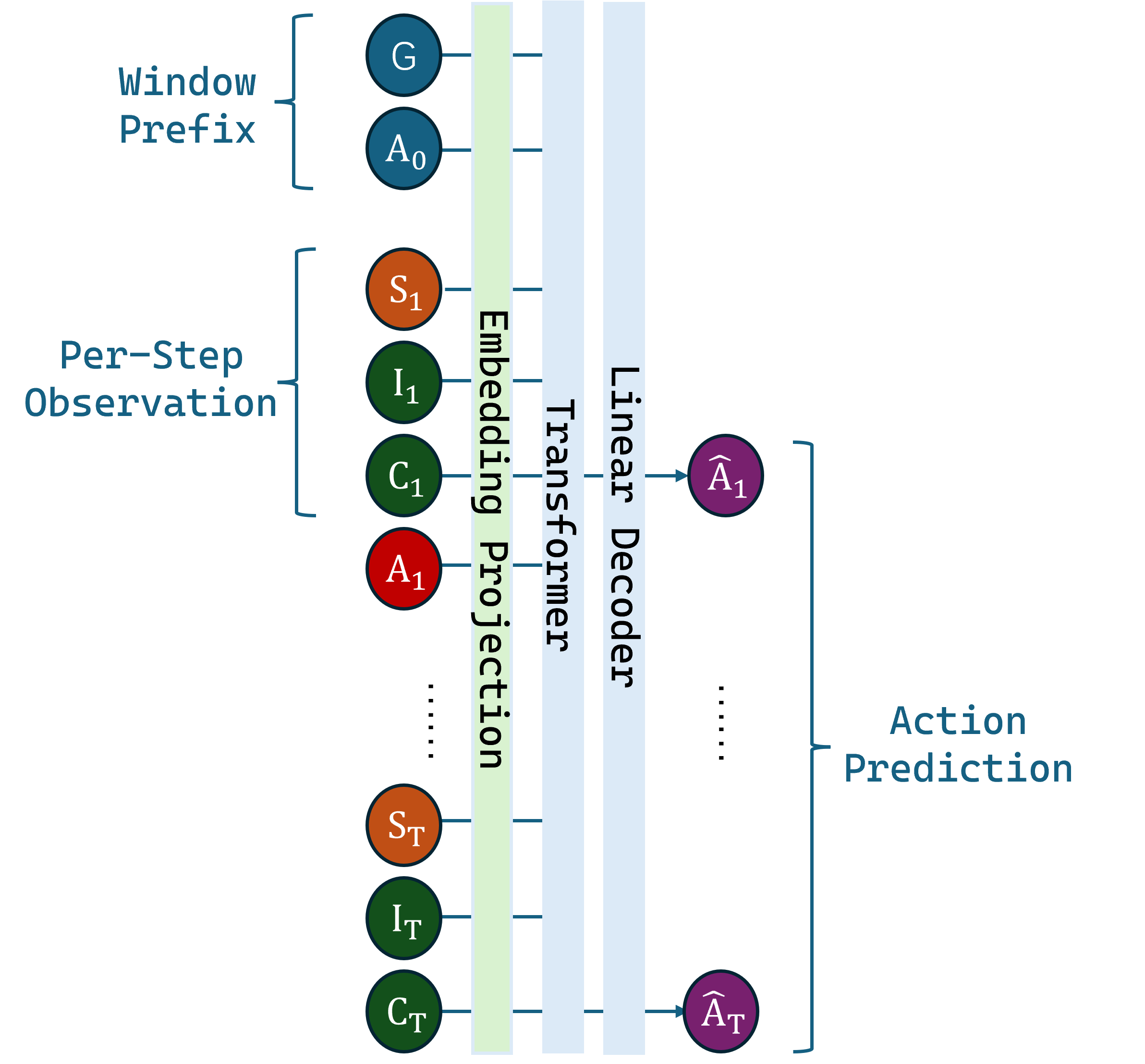
This paper introduces Incremental Signature Contribution (ISC), a method for representing sequential data that enhances model sensitivity and effectiveness in offline RL.
While path signatures offer a powerful, universal representation for sequential data, their inherent collapse of temporal structure limits their application in decision-making tasks demanding reactivity and sensitivity. This work, ‘From Path Signatures to Sequential Modeling: Incremental Signature Contributions for Offline RL’, addresses this limitation by introducing the Incremental Signature Contribution (ISC) method, which decomposes signatures into a temporally ordered sequence reflecting incremental changes along a trajectory. ISC preserves the algebraic expressiveness of signatures while explicitly revealing their internal temporal evolution, enabling effective integration with sequential modeling approaches like Transformers. Does this novel representation unlock improved performance and stability in offline reinforcement learning for temporally sensitive control problems?
The Fading Echo of Time: Capturing Sequential Data
Many conventional techniques for analyzing time series data – whether financial markets, physiological signals, or climate patterns – often fall short when confronted with the intricacies of real-world phenomena. These methods frequently rely on summarizing data through discrete points or statistical moments, effectively discarding crucial information about the path the data takes over time. This simplification leads to a significant loss of detail, particularly in irregular or high-frequency datasets where the order and geometric properties of the data are paramount. For example, a stock price might be represented by its daily closing value, obscuring the intraday fluctuations that reveal trading patterns and volatility. Similarly, analyzing a patient’s heart rate solely through average beats ignores the subtle variations that could indicate underlying health issues. Consequently, these traditional approaches struggle to accurately model and predict complex systems, highlighting the need for more sophisticated representation techniques that preserve the full sequential information embedded within the data.
Path signatures offer a fundamentally different approach to analyzing sequential data, moving beyond methods that treat time series as simple lists of values. This technique leverages the principles of rough path theory to meticulously capture the geometric features embedded within a path – not just its overall length or endpoints, but also the area swept by the path, its iterated integrals, and higher-order relationships. Essentially, a path signature transforms a trajectory into a hierarchy of increasingly refined descriptors, preserving the order of events and the way the path twists and turns through space. This is achieved through the calculation of \in t_0^T X_t dX_t and its iterated integrals, creating a complete and discriminating fingerprint of the path’s shape. Unlike simpler representations that often discard crucial information about the path’s internal structure, path signatures provide a robust and expressive framework, enabling more accurate modeling and analysis of complex, irregular time series data.
Log-Signatures represent a significant advancement in the computational handling of complex sequential data. While Path Signatures effectively capture the intricacies of irregular time series, their inherent redundancies can limit scalability. Log-Signatures address this by applying a mathematical transformation – specifically, taking the logarithm of the iterated integrals – which removes these redundancies without diminishing the expressive power of the representation. This process streamlines computations, allowing for the efficient analysis of lengthy and high-dimensional paths that would be intractable with standard Path Signatures. The resulting Log-Signature remains a complete characterization of the path’s geometric and temporal information, but in a more compact and computationally friendly form, enabling applications in areas like financial modeling, medical diagnostics, and robotics where real-time analysis of complex data streams is crucial. Essentially, \log(\text{Path Signature}) provides a powerful balance between accuracy and efficiency.
Signature-Enhanced Neural Networks: A New Paradigm for Temporal Understanding
Deep Signature Transforms introduce a novel approach to pooling sequential data within neural networks by utilizing path signatures. These signatures, derived from iterated integrals along the sequence’s path, provide a complete characterization of the path’s shape and allow the network to capture long-range dependencies without being limited by fixed-size windows or recurrent connections. Crucially, the signature computation is differentiable, enabling gradient-based optimization throughout the network. This allows the network to learn which features of the sequence are most relevant, effectively performing a form of attention during the pooling process and selectively focusing on informative parts of the input sequence. The resulting signature vector serves as a fixed-length representation of the sequence, suitable for downstream tasks while retaining information about the sequence’s geometric properties.
Neural Continuous-time Dynamical Equations (Neural CDEs) and Neural Residual Differential Equations (Neural RDEs) employ path signatures as a mechanism for summarizing long sequential data. Traditional recurrent neural networks struggle with long sequences due to vanishing gradients and computational demands; Neural CDEs and RDEs address this by representing the sequence’s evolution as a continuous dynamical system. Path signatures, derived from the iterated integrals of the path, provide a fixed-dimensional, order-invariant summary of the entire trajectory, effectively capturing the sequence’s history. This approach allows for efficient processing of sequences with irregular time steps, as the signature calculation is independent of the sampling rate. Furthermore, the fixed-dimensional signature representation significantly reduces the computational burden associated with processing long sequences compared to methods that retain the full sequence history.
Rough Transformers improve upon standard attention mechanisms through the integration of signature patching and multi-view signature attention. Signature patching condenses sequential data into a lower-dimensional representation using path signatures, thereby reducing computational complexity. Multi-view signature attention then leverages these signatures, computed from multiple randomly projected views of the input sequence, to create a more robust and informative attention context. This approach allows the model to capture long-range dependencies and hierarchical structures within the data, resulting in enhanced performance on complex sequential tasks compared to traditional Transformer architectures.
Offline Reinforcement Learning: Navigating Uncertainty with Incremental Signatures
Offline Reinforcement Learning (RL) addresses scenarios where interaction with the environment is costly or impossible, enabling policy learning solely from pre-collected, static datasets. However, a significant challenge arises from the limited diversity and potential biases present in these datasets; policies must generalize effectively beyond the observed data distribution. This necessitates the development of robust algorithms capable of accurately estimating the value function and policy outside the scope of the training data, as standard RL methods can suffer from extrapolation errors when encountering states or actions not well-represented in the offline dataset. Consequently, techniques such as conservative policy optimization and behavior regularization are often employed to mitigate the risk of out-of-distribution actions and improve the reliability of learned policies in offline settings.
The Incremental Signature Contribution (ISC) addresses computational limitations associated with traditional path signature representations in Reinforcement Learning. Path signatures, while capable of capturing trajectory history, scale poorly with trajectory length due to their global nature. ISC decomposes these signatures into a series of time-indexed contributions, effectively representing the trajectory as a sequence of incremental changes. This decomposition facilitates efficient computation and storage, as only the changes at each time step are stored rather than the entire cumulative signature. The resulting representation maintains the information content of the global signature while significantly reducing computational complexity, thereby enabling the processing of longer and more complex trajectories within offline Reinforcement Learning frameworks.
The Incremental Signature Contribution Transformer (ISCT) builds upon the architecture of the Decision Transformer (DT) by integrating representations derived from Incremental Signature Contributions (ISCs). This modification addresses limitations in offline reinforcement learning where data scarcity hinders generalization. By incorporating ISC representations, which decompose trajectories into time-indexed components, ISCT enhances the model’s ability to learn from limited datasets. This results in improved sample efficiency and demonstrable gains in policy performance compared to standard offline RL algorithms such as DT and CQL, particularly in environments with delayed rewards. The ISCT architecture leverages the time-series properties captured within the ISC to provide a more robust and informative input to the transformer network, ultimately leading to better policy learning.
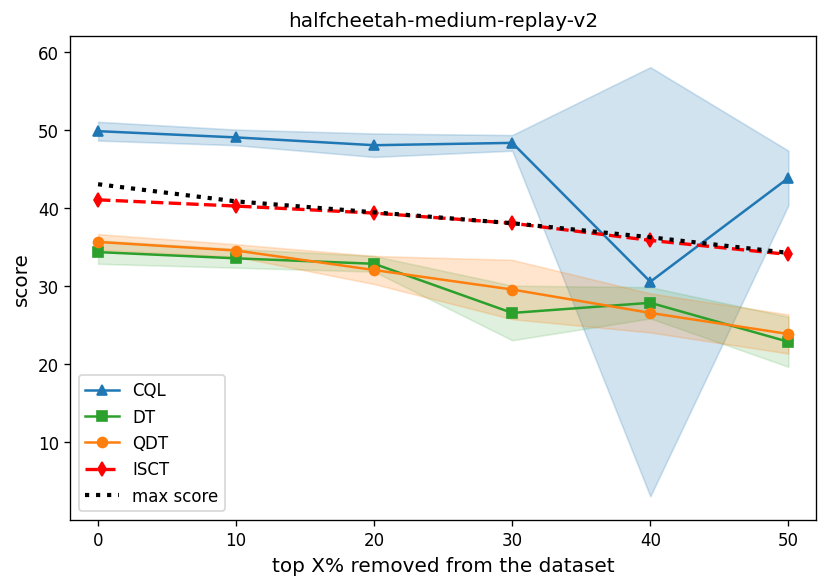
The Incremental Signature Contribution Transformer (ISCT) has been evaluated across a range of benchmark reinforcement learning environments, including continuous control tasks like HalfCheetah, Hopper, and Walker2d, as well as discrete navigation challenges presented by Maze2d. Notably, ISCT maintains consistent performance levels even when faced with delayed reward structures, a condition under which standard offline reinforcement learning algorithms such as Decision Transformer (DT) and Conservative Q-Learning (CQL) often exhibit diminished results. This resilience to reward delay suggests that ISCT’s incremental signature representation effectively captures and propagates relevant information throughout trajectories, enabling robust policy learning from static datasets.
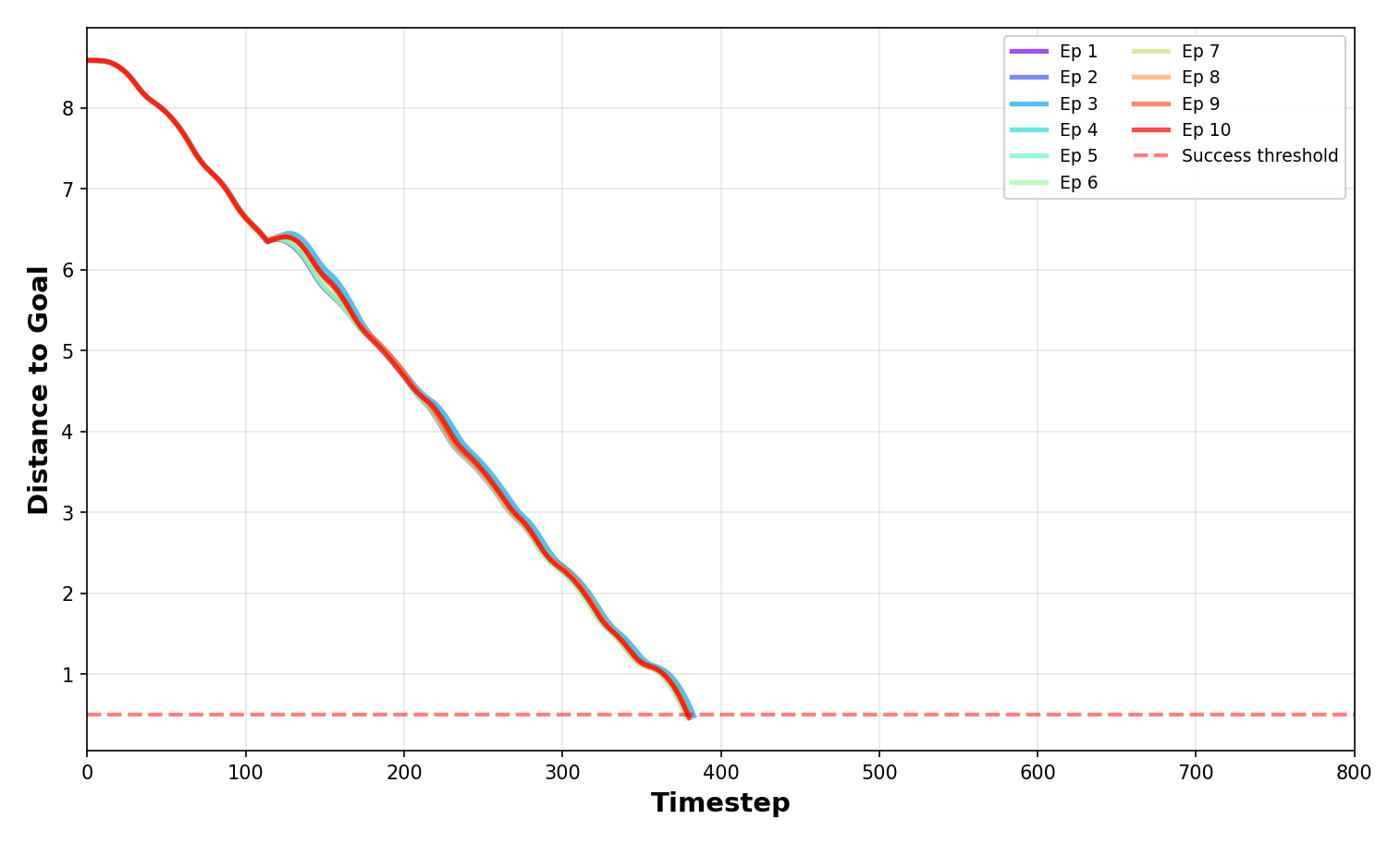
Evaluations conducted on a downgraded HalfCheetah dataset demonstrate the superior performance of the Incremental Signature Contribution Transformer (ISCT) relative to the Decision Transformer (DT). Specifically, ISCT maintains consistent tracking performance throughout the training process, indicating improved robustness and stability in learning from limited or suboptimal data. This outcome suggests that the incorporation of incremental signature contributions effectively addresses the challenges associated with offline reinforcement learning, enabling more reliable policy learning even when faced with data deficiencies that would typically hinder the Decision Transformer’s ability to accurately follow the desired trajectory.
Evaluation on Maze2d environments quantitatively demonstrates the efficacy of the Incremental Signature Contribution Transformer (ISCT). Specifically, ISCT achieves statistically significant reductions in average path length required to solve the maze, indicating improved navigational efficiency compared to baseline algorithms. As visually represented in Figure 4, ISCT consistently exhibits shorter path lengths across varying maze configurations and difficulty levels. This reduction in path length serves as a direct measure of policy performance, confirming that ISCT learns more effective strategies for navigating the maze environment from the offline dataset.
Generative Horizons: Distilling Time’s Essence with Signatures
SigDiffusions represent a notable advancement in generating complex, multivariate time series data by leveraging the principles of score-based diffusion models within the framework of log-signature embeddings. This approach effectively transforms raw time series into a lower-dimensional, information-rich space – the log-signature – allowing the diffusion process to operate more efficiently and capture intricate dependencies. Unlike traditional methods that often struggle with high-dimensional data or require explicit modeling of complex relationships, SigDiffusions learn the underlying data distribution implicitly through a denoising process. The technique begins with random noise and iteratively refines it, guided by the score function – the gradient of the log-density – to ultimately produce realistic and coherent time series. This allows for the generation of entirely new time series exhibiting characteristics similar to the training data, offering significant potential in applications ranging from financial modeling and climate prediction to robotic control and medical diagnostics.
Truncated signatures offer a surprisingly efficient pathway to capturing complex, nonlinear dynamics within time series data. This stems from the inherent “Universal Nonlinearity Approximation” property, which mathematically guarantees that even a relatively short signature – a condensed representation of the time series’ path – can approximate any continuous function to a desired degree of accuracy. Consequently, models leveraging truncated signatures don’t require vast computational resources to achieve expressive power; they can effectively model intricate relationships without the parameter explosion often associated with deep learning approaches. This efficiency is crucial for real-world applications where computational constraints are paramount, allowing for deployment on edge devices or within resource-limited environments while still maintaining robust performance in tasks such as forecasting and anomaly detection. The ability to distill complex information into a compact, yet expressive, form represents a significant advancement in time series analysis.
The recent progress in generative modeling of time series data, particularly through techniques like SigDiffusions and the utilization of log-signature embeddings, is poised to significantly impact several applied fields. Time series forecasting, crucial for predicting future values in areas ranging from finance to weather patterns, stands to benefit from the ability to generate realistic and diverse future scenarios. Furthermore, the nuanced representations learned by these models enhance anomaly detection capabilities, allowing for the identification of unusual patterns indicative of fraud, equipment failure, or other critical events. Perhaps most notably, these advancements are creating new possibilities within control systems, where generative models can be used to simulate system behavior, optimize control strategies, and even design robust controllers capable of adapting to unforeseen circumstances – ultimately enabling more intelligent and responsive automated systems.
Rigorous ablation studies highlight the critical role of Incremental Signature Contributions (ISC) in the generative modeling framework. Replacing ISC tokens – which capture the evolving geometry of the time series – with simpler correlation-based features led to a substantial and demonstrable performance decline. This suggests that the nuanced, path-dependent information encoded within the ISC tokens is not merely redundant, but fundamentally necessary for accurate and high-fidelity time series generation. The results underscore that capturing how changes accumulate over time, rather than simply static relationships between variables, is paramount for effectively modeling complex, multivariate temporal data. This finding reinforces the importance of signature-based methods in preserving crucial dynamic information often lost in traditional approaches.
Research indicates that generative models perform suboptimally when provided with complete signature information at each step, rather than incremental signature contributions (ISC). This suggests the model benefits from processing information in a sequential, nuanced manner, effectively learning the evolving relationships within the time series. Providing the full signature at once appears to overwhelm the generative process, hindering its ability to accurately capture the dynamics and dependencies crucial for successful data generation. The model seems to rely on the incremental changes captured by ISC to build a coherent understanding of the time series’ structure, and dispensing with this feature leads to a noticeable decline in performance, highlighting the importance of temporal context in multivariate data generation.
The pursuit of robust sequential modeling, as demonstrated in this work concerning path signatures and offline reinforcement learning, echoes a fundamental truth about complex systems. Just as architectures inevitably evolve and change, so too must representations of temporal data adapt to capture nuanced dynamics. Robert Tarjan aptly observes, “The most important things are the things you don’t know.” This sentiment resonates with the core idea of capturing temporal dependencies through incremental signature contributions; the method acknowledges that complete knowledge of a sequence is often unattainable, and focuses on effectively representing what can be learned from its evolving signature. It’s a recognition that improvement, while desirable, occurs within the constraints of incomplete information and an ever-changing landscape.
What Lies Ahead?
The pursuit of sequential understanding, as demonstrated by this work, inevitably encounters the limits of representation. While path signatures offer a compelling means of distilling temporal information, the inherent truncation-the loss of fidelity in converting continuous paths to finite signatures-remains a persistent challenge. Future investigations must address not merely the length of these signatures, but the wisdom of their construction; every added term is a trade-off between expressive power and computational cost, and the optimal balance will likely be problem-dependent. The architecture, however elegant, is only as resilient as its grounding in the underlying dynamics.
The integration of ISC with Transformer networks represents a logical step, yet the potential for architectural bias should not be dismissed. Sensitivity is a virtue, but only when calibrated against robustness. The true test lies in applying this methodology to systems characterized by genuine ambiguity and non-stationarity – environments where the past offers imperfect guidance for the future. The value isn’t simply in predicting outcomes, but in gracefully accommodating the inevitable deviations.
Ultimately, the field must move beyond benchmarks focused on idealized sequences. Every delay in pursuing more complex, realistic scenarios is, paradoxically, the price of deeper understanding. A model that excels in simulation but falters in the presence of genuine entropy is a beautiful, yet fragile, artifact. The long game isn’t about achieving perfect recall, but about building systems that age with a measure of dignity.
Original article: https://arxiv.org/pdf/2602.11805.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- One Piece Chapter 1174 Preview: Luffy And Loki Vs Imu
- Top 8 UFC 5 Perks Every Fighter Should Use
- How to Build Muscle in Half Sword
- How to Play REANIMAL Co-Op With Friend’s Pass (Local & Online Crossplay)
- Violence District Killer and Survivor Tier List
- Mewgenics Tink Guide (All Upgrades and Rewards)
- Epic Pokemon Creations in Spore That Will Blow Your Mind!
- Bitcoin’s Big Oopsie: Is It Time to Panic Sell? 🚨💸
- All Pistols in Battlefield 6
- Unlocking the Secrets: What Fans Want in a Minecraft Movie Sequel!
2026-02-15 06:23