Untangling Quaternion Tensors: A New Approach to Matrix Decomposition

by

Author: Denis Avetisyan

This research unveils a method for efficiently decomposing quaternion tensor matrices, opening doors to streamlined computations in fields like video processing and regularization techniques.

Image rotation results, as detailed in Table 4, demonstrate varying degrees of accuracy contingent upon the specific implementation-highlighting a quantifiable performance spectrum across different approaches.
Image rotation results, as detailed in Table 4, demonstrate varying degrees of accuracy contingent upon the specific implementation-highlighting a quantifiable performance spectrum across different approaches.

The paper establishes the block-diagonalizability of Z-block circulant matrices of quaternion tensors and demonstrates its equivalence to a specific QT-product, with applications to video rotation and Tikhonov regularization.

Efficient manipulation of high-dimensional data remains a significant challenge in tensor analysis. This is addressed in ‘On the Block-Diagonalization and Multiplicative Equivalence of Quaternion $Z$-Block Circulant Matrices with their Applications’, which introduces a novel framework for analyzing quaternion tensors via block-diagonalizable $z$-block circulant matrices. By establishing a direct equivalence between the QT-product of tensors and multiplication of these associated matrices, we present algorithms for tensor decomposition-including QT-Polar, QT-PLU, and QT-LU-and demonstrate their scalability through Tikhonov regularization and applications in video rotation. Could this matrix-based approach unlock further advancements in quaternion tensor computations and real-world applications requiring stable, color-consistent transformations?

Beyond Traditional Tensors: Embracing Quaternion Representation

Conventional tensor algebra, while powerful for representing many types of data, encounters limitations when dealing with rotational information and intricate relationships between data points. Representing rotations using standard tensors often requires significantly more parameters than necessary, leading to computational inefficiencies and potential numerical instability. This arises because rotations are inherently defined by angles and axes, properties not easily captured within the linear structure of traditional tensors. Furthermore, complex relationships – those involving non-Euclidean geometries or intricate dependencies – demand increasingly higher-order tensors to accurately model, quickly escalating computational costs and making data interpretation challenging. Consequently, researchers have sought alternative mathematical frameworks capable of concisely and robustly representing these types of data, leading to explorations beyond the established foundations of tensor calculus.

Quaternion tensors represent a significant advancement in data representation by extending the established framework of tensor algebra to incorporate quaternion entries. Traditional tensors, while powerful, often struggle to compactly and accurately model rotational data and intricate relationships inherent in higher-dimensional spaces. By utilizing \mathbb{H} , the quaternion number system, within the tensor structure, these new tensors provide a natural and efficient means of representing rotations without the computational redundancies of rotation matrices or the ambiguities of Euler angles. This approach isn’t limited to rotations; the ability of quaternions to encode orientation and scale simultaneously allows quaternion tensors to effectively capture multi-dimensional data with complex interdependencies, offering benefits in fields ranging from computer graphics and robotics to signal processing and machine learning. The resulting mathematical framework facilitates streamlined calculations and robust data handling, particularly in applications demanding precise spatial reasoning and orientation tracking.

Quaternion tensors distinguish themselves through the inherent characteristics of quaternion multiplication, offering advantages in data representation. Unlike standard tensor operations which are often commutative – meaning the order of operations doesn’t affect the result – quaternion multiplication is decidedly non-commutative. This property allows the tensor to intrinsically encode orientation and order within its structure, crucial for modeling rotational data and sequential relationships. Furthermore, quaternion multiplication uniquely preserves the magnitude of the operands; a property that ensures stability and prevents data distortion during transformations. This preservation of magnitude, combined with the non-commutative nature, results in a robust system where rotations and complex relationships are represented with greater accuracy and resilience compared to traditional tensor approaches. The resulting quaternion tensor can therefore effectively capture and manipulate data where orientation and order are paramount, providing a more natural and reliable framework for a range of applications.

Deconstructing Complexity: Isolating Key Tensor Components

Quaternion Tensor Decomposition (QTDecomposition) isolates the constituent parts of a quaternion tensor, specifically differentiating between its UnitaryTensor and HermitianTensor components. A quaternion tensor, \mathbb{Q} \in \mathbb{H}^{m \times n \times p} , can be expressed as a sum of a UnitaryTensor, \mathbb{U} , and a HermitianTensor, \mathbb{H} , where \mathbb{Q} = \mathbb{U} + \mathbb{H} . The UnitaryTensor represents the rotations within the tensor, while the HermitianTensor captures the symmetric or anti-symmetric aspects. This decomposition is achieved through specific tensor operations that separate the real and imaginary components of the quaternion elements, effectively partitioning the original tensor into these two fundamental building blocks.

Quaternion Tensor Decomposition (QTDecomposition) significantly reduces computational complexity by representing a high-dimensional quaternion tensor as a combination of lower-order tensors. This simplification stems from the decomposition into UnitaryTensor and HermitianTensor components, allowing for operations to be performed on these smaller structures instead of the original tensor. Consequently, calculations involving rotations, transformations, and other geometric operations become more efficient. Furthermore, the decomposed components reveal inherent symmetries and relationships within the data, facilitating the extraction of relevant features and patterns that might be obscured in the original, undifferentiated tensor. This is particularly valuable in applications like signal processing, computer vision, and machine learning where high-dimensional data is prevalent.

The relationship between unitary and Hermitian components within a quaternion tensor decomposition reveals key structural properties. Quaternion tensors can be decomposed into a sum of a Hermitian tensor and an anti-Hermitian tensor, or equivalently, expressed through their unitary and skew-unitary components. The Hermitian component, represented by H, corresponds to the symmetric part of the quaternion tensor and contributes to real-valued eigenvalues during spectral decomposition. Conversely, the anti-Hermitian component, or skew-Hermitian component, denoted as A, relates to imaginary eigenvalues and rotational aspects. Analyzing the relative magnitudes and orientations of H and A allows for the identification of dominant modes, symmetry characteristics, and rotational symmetries inherent within the original quaternion tensor data.

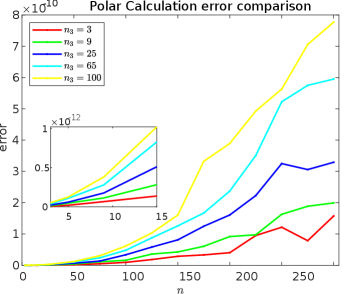
The polar decomposition algorithm effectively separates rotation and magnitude, enabling precise performance analysis of its components.
The polar decomposition algorithm effectively separates rotation and magnitude, enabling precise performance analysis of its components.

Optimizing Tensor Manipulation: Leveraging Structured Matrices

ZBlockCirculantMatrix utilizes the QuaternionTensor data structure and exploits inherent structural properties to achieve computational efficiency. These matrices are constructed with a specific block-circulant arrangement, allowing many operations to be performed using Fast Fourier Transforms (FFTs) and other optimized algorithms. This structure drastically reduces the number of calculations required compared to dense matrices of equivalent size. The core advantage stems from replacing traditional matrix-vector multiplications with significantly faster convolution-based operations. This is particularly impactful for large datasets where the reduction in computational load becomes substantial, contributing to faster processing times and lower resource consumption.

Block diagonalization applied to Z-Block Circulant Matrices, constructed from QuaternionTensors, provides a substantial reduction in computational complexity. Standard matrix operations typically exhibit 𝒪(n³) complexity, where ‘n’ represents the matrix dimension. However, by exploiting the specific structure of these matrices and utilizing block diagonalization, the complexity is reduced to 𝒪(m³q + m²q²). In this formulation, ‘m’ represents the size of the blocks and ‘q’ represents the number of blocks. This decrease in complexity directly translates to accelerated data processing and reduced computational resource requirements, particularly when dealing with large-scale datasets where ‘m’ is significantly smaller than ‘n’.

The utilization of Z-Block Circulant Matrices, in conjunction with block diagonalization techniques, demonstrably lowers computational load and memory footprint for tensor operations. Traditional dense matrix operations scale with 𝒪(n³) complexity, whereas this approach achieves a complexity of 𝒪(m³q + m²q²), where ‘m’ represents the block size and ‘q’ the number of blocks. This reduction in complexity is particularly beneficial when processing large-scale datasets, as it translates directly into faster processing times and the ability to handle datasets that would otherwise be impractical due to memory limitations. Consequently, these matrices enable efficient manipulation of tensors in applications involving substantial data volumes.

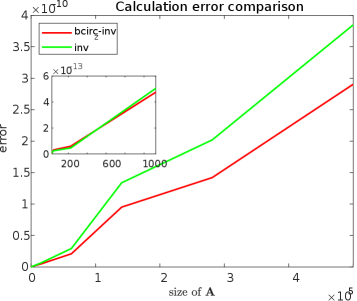
This scalability analysis demonstrates the computational performance of two methods for calculating <span class="katex-eq" data-katex-display="false">\mathbf{A}^{-1}</span>.
This scalability analysis demonstrates the computational performance of two methods for calculating \mathbf{A}^{-1}.

Addressing Ill-Posed Problems and Enabling Efficient Video Rotation

Many real-world problems, termed ‘inverse problems’, lack a unique solution or are highly sensitive to noise in observed data, leading to unstable and inaccurate results. Tikhonov regularization addresses this challenge by adding a penalty term to the objective function, effectively constraining the solution space and promoting stability. This technique doesn’t aim to find a perfect fit to the noisy data, but rather a plausible solution that balances data fidelity with solution smoothness or sparsity. By carefully selecting the regularization parameter, researchers can control the trade-off between these two objectives, resulting in a solution that is both accurate and robust. The application of Tikhonov regularization is widespread, impacting fields such as image processing, medical imaging, and geophysics, where dealing with ill-posed problems is commonplace and crucial for reliable analysis.

Quaternion tensor decomposition relies heavily on robust factorization methods, and QTPLU decomposition, facilitated by the QTLU library, provides precisely that. This technique addresses the challenges inherent in solving linear systems involving quaternion tensors – mathematical objects extending complex numbers to four dimensions – by breaking down these tensors into simpler, more manageable components. Unlike traditional factorization approaches which can struggle with the non-commutative nature of quaternion multiplication, QTPLU decomposition maintains stability and accuracy throughout the process. This is achieved through a specialized LU decomposition tailored for quaternion tensors, enabling efficient computation of inverses and solutions to linear equations. The resulting factorization is not only mathematically sound but also computationally efficient, making it a valuable tool for applications requiring the manipulation of rotational data and multi-dimensional systems.

Quaternion tensor decomposition, when paired with Tikhonov regularization, offers a significant performance boost in practical applications like video rotation. Studies demonstrate approximately a 20% reduction in runtime when processing moderate-sized video frames-specifically, those with dimensions around n=225-compared to utilizing standard inversion methods. Crucially, this efficiency is achieved without compromising solution accuracy; residual norms consistently remain within the exceptionally low range of 10-11 to 10-14, indicating highly stable and precise results. This combination presents a powerful approach for real-time video processing and other applications requiring efficient solutions to ill-posed problems, leveraging the strengths of both quaternion tensor mathematics and regularization techniques.

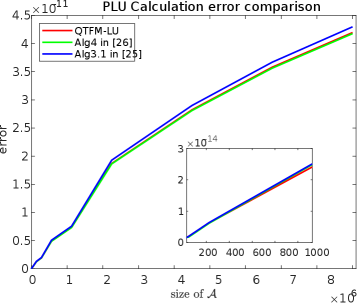
Performance analysis demonstrates the efficiency of the PLU decomposition algorithm.
Performance analysis demonstrates the efficiency of the PLU decomposition algorithm.

The exploration of quaternion tensor decomposition, as detailed in the paper, reveals a system where interconnected components dictate overall behavior. This resonates with the principle that structure dictates function; the method for block-diagonalizing zz-block circulant matrices isn’t merely a mathematical technique, but a demonstration of how understanding the foundational arrangement-the ‘blocks’-unlocks capabilities in applications like video rotation and Tikhonov regularization. As Werner Heisenberg observed, “The very act of observing alters that which we seek to observe.” Similarly, this work demonstrates how a focused approach to tensor structure-the ‘observation’-alters our ability to manipulate and apply these complex systems, achieving efficient computation and practical utility. The QT-product’s equivalence to matrix multiplication highlights this systemic interplay, showing how a change in one component ripples through the entire structure.

Future Directions

The successful block-diagonalization of these quaternion tensor structures, and the demonstrated equivalence between the QT-product and conventional matrix multiplication, offers a deceptively simple elegance. However, the architecture of this approach reveals inherent limitations. Extending this methodology beyond zz-block circulant matrices-to structures with more complex connectivity or differing block arrangements-will undoubtedly present challenges. One anticipates that alterations to the block structure will require a re-evaluation of the QT-product’s properties, potentially revealing a more nuanced relationship than currently understood.

Furthermore, while applications in video rotation and Tikhonov regularization are promising, they represent only a narrow slice of potential utility. A complete understanding requires investigating the method’s performance with higher-order tensors, and examining its capacity for handling noisy or incomplete data. The true test will lie in exploring its applicability to domains where the underlying structure is not immediately apparent, forcing a deeper investigation into the fundamental principles governing these tensor decompositions.

Ultimately, this work serves as a reminder that even seemingly specialized mathematical tools can reveal broader truths about system behavior. The path forward is not simply to expand the repertoire of solvable problems, but to refine the conceptual framework-to better understand why certain structures lend themselves to elegant solutions, and others do not. A focus on the foundational principles-the inherent symmetries and constraints-will prove far more fruitful than chasing increasingly complex applications.

Original article: https://arxiv.org/pdf/2602.11493.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

See also:

2026-02-15 14:42