Scaling Electronic Correlation to Nanoscale Systems

Author: Denis Avetisyan

A new computational method efficiently tackles the complex problem of calculating electronic correlation energies in large, complex materials.

The stochastic cluster expansion method accurately models the total correlation energy throughout the Menshutkin reaction-the transfer of a methyl group from methyl chloride to ammonia, forming methylammonium and chloride-achieving this for a defined five-orbital occupied subspace and eight-orbital unoccupied subspace, and quantifying uncertainty through standard error calculated across twenty-five stochastic samples.

This work introduces the Stochastic Cluster Expansion (SCE) – a technique combining stochastic sampling and downfolding to improve the efficiency of electronic structure calculations.

Accurate modeling of electronic correlation in extended systems remains a significant challenge due to the exponential scaling of many-body methods with system size. This work introduces a Stochastic Cluster Expansion (SCE) framework-detailed in ‘A Stochastic Cluster Expansion for Electronic Correlation in Large Systems’-to efficiently and accurately recover total correlation energies without a priori selection of an active space. By combining stochastic sampling with a cluster expansion of the correlation energy, SCE achieves near-density matrix renormalization group (DMRG) accuracy at drastically reduced computational cost. Will this approach unlock high-accuracy simulations of complex chemical processes in condensed-phase environments previously inaccessible to detailed quantum mechanical treatment?

The Limits of Correlation: Peering into the Quantum Abyss

The accurate modeling of many-body quantum systems is fundamentally limited by the complexity of electron correlation – the intricate interplay between electrons that dictates a material’s properties. While the Schrödinger equation perfectly describes these systems in theory, its solution demands computational resources that scale exponentially with the number of interacting particles. This arises because each electron’s behavior is inextricably linked to all others, necessitating a consideration of an enormous number of possible electron configurations. Consequently, even modest-sized systems quickly become intractable for exact solution, forcing researchers to rely on approximations that inevitably introduce errors and limit the predictive power of computational materials science. Capturing these subtle, yet crucial, correlations remains a central challenge in understanding and designing novel materials with desired functionalities, pushing the boundaries of both theoretical development and computational infrastructure.

Wavefunction-based methods, such as Configuration Interaction and Coupled Cluster, represent a cornerstone of quantum chemistry due to their potential for high accuracy. However, a fundamental limitation arises from the inherent complexity of describing many-electron systems; the computational cost of these approaches scales exponentially with the number of electrons, or equivalently, the system size. This exponential scaling stems from the need to account for all possible electron configurations, which grows factorially. Consequently, applying these methods to realistic materials and molecules – those containing even a moderate number of atoms – quickly becomes intractable, even with the most powerful supercomputers. While approximations can be employed, they often compromise accuracy or introduce systematic errors, highlighting the need for alternative computational strategies that can overcome this scaling bottleneck and enable the study of complex quantum phenomena.

Mean-field electronic structure methods, such as Hartree-Fock and density functional theory, simplify the complex many-body problem by approximating each electron as moving in an average field created by all other electrons. This approach dramatically reduces computational cost, enabling simulations of larger systems. However, this simplification comes at a price; these methods struggle when electrons exhibit strong interactions or become highly localized – situations where the average field approximation breaks down. In such cases, crucial details arising from instantaneous electron-electron correlations are lost, leading to inaccurate predictions of material properties and chemical behavior. For example, strongly correlated materials like high-temperature superconductors and certain transition metal oxides require methods beyond the mean-field approximation to accurately capture their exotic electronic states and behaviors, highlighting the limitations of this widely used approach when dealing with complex quantum phenomena.

The correlation between single-particle states localized on solvent molecules decreases with increasing distance from the metaphosphate, as illustrated by the density of states in panels A-D and confirmed by standard error measurements across 25 stochastic samples.

Deconstructing Complexity: Partitioning the Quantum Realm

Downfolding and embedding techniques address computational scaling issues in electronic structure calculations by dividing a system into an ‘active’ region – representing the area of primary interest, such as a reaction center or a specific molecule – and an ‘environment’ comprising the remaining degrees of freedom. The environment is then modeled using a lower-cost, approximate method, significantly reducing the overall computational demands. This partitioning allows for high-accuracy calculations on the active region, while treating the influence of the surrounding environment with reduced computational effort; the accuracy of the environment representation directly impacts the overall result, necessitating careful consideration of the chosen methodology and its limitations.

Ab initio embedding methods represent a computationally rigorous approach to partitioning complex systems by treating a localized ‘active’ region with a high level of theory derived directly from first principles, while the surrounding ‘environment’ is modeled with a less demanding, and potentially empirical, method. This approach ensures accuracy within the active region without the prohibitive cost of applying the high-level theory to the entire system. However, even with this partitioning, the calculations remain computationally demanding due to the need for self-consistency between the active and environment regions; this requires iterative solving of the electronic structure problem until convergence is achieved, and the scaling of the calculations with system size can still be significant, particularly for strongly correlated systems or large active regions.

Localized Active Space (LAS) methods build upon downfolding and embedding techniques by further partitioning the initially defined ‘active’ region into even smaller, chemically relevant fragments. This refinement focuses computational resources on the most critical correlation effects-typically those arising from localized bonds, lone pairs, or open-shell character-while treating the remaining portions of the active region with a simpler, lower-cost approximation. By explicitly targeting these key interactions, LAS methods achieve a more favorable trade-off between accuracy and computational efficiency compared to broader active space treatments, enabling the study of larger systems or longer timescales that would otherwise be inaccessible. The selection of these localized fragments is often guided by chemical intuition or automated analysis of the system’s wavefunction to identify regions exhibiting strong correlation.

A cluster expansion fully describes the free energy surface, while a lower-order truncation approximates it using stochastically sampled regions.

Randomness as a Tool: The Stochastic Cluster Expansion Unveiled

The Cluster Expansion is a method for calculating the correlation energy in many-body quantum systems by systematically organizing contributions based on groupings of single-particle states. This approach decomposes the total correlation energy into a sum of cluster contributions, each representing the energy associated with a specific grouping – or “cluster” – of occupied and virtual single-particle orbitals. The energy of each cluster is then calculated and summed to approximate the total correlation energy. This organization allows for a hierarchical treatment of electron correlation effects, starting with the most important contributions arising from lower-order clusters and progressively incorporating higher-order terms to improve accuracy. The method inherently separates the problem into manageable components based on the excitation level within the chosen single-particle basis, providing a structured pathway to account for electron correlation beyond the Hartree-Fock approximation.

The Stochastic Cluster Expansion (SCE) enhances computational efficiency by employing randomized sampling of single-particle orbitals to approximate the many-body wavefunction. This technique effectively reduces the computational scaling associated with explicitly treating electron correlation, as the number of determinants contributing to the wavefunction is significantly compressed. Benchmarking demonstrates that SCE achieves a computational speedup of up to 86% for systems containing 80 electrons when compared to exact Diagonalization and Density Matrix Renormalization Group (DMRG) calculations, representing a substantial reduction in required computational resources for similarly sized systems.

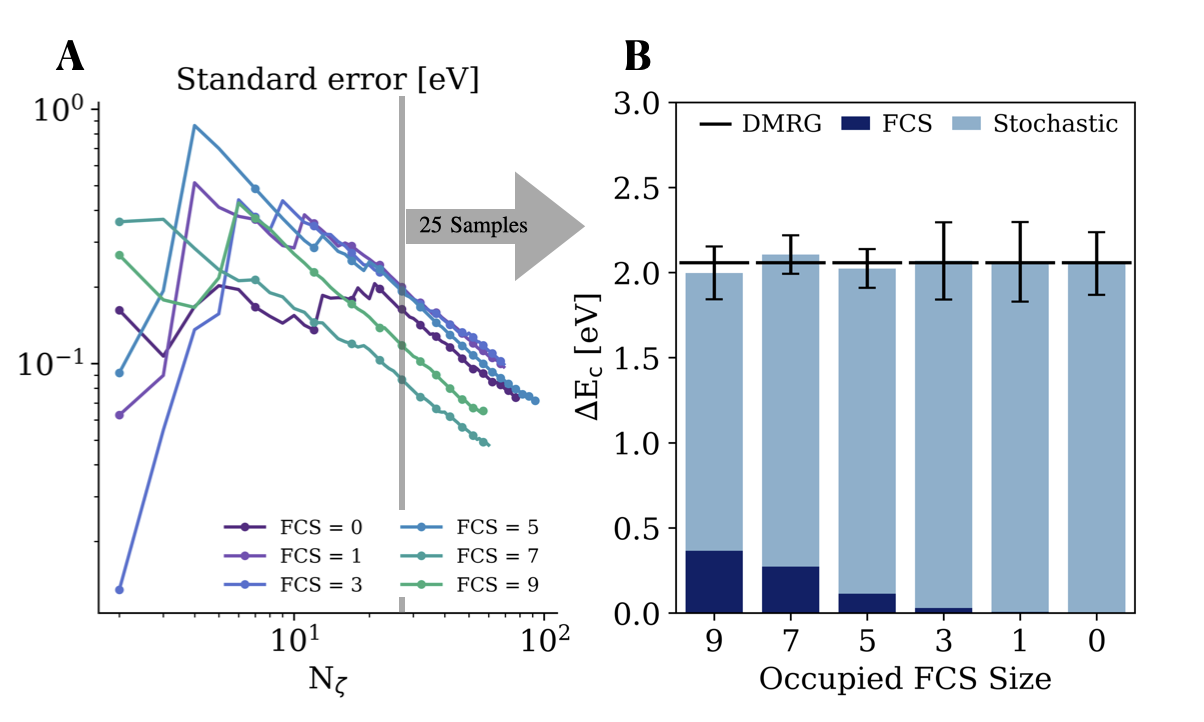
The Stochastic Cluster Expansion (SCE) is mathematically grounded in the structure of the Hilbert space describing the many-body system. This allows for a controlled approximation of the complete wavefunction through randomized sampling. Specifically, the method’s accuracy scales inversely with the number of samples, $N$ , and a parameter, ζ, representing the statistical error. Empirical results demonstrate that approximately 25 samples are sufficient to achieve an error decay proportional to $1/N\zeta$ , providing a rigorous and quantifiable pathway to approximate the solution while maintaining computational efficiency.

The stochastic cluster expansion method accurately calculates the total correlation energy of a solvated sodium metaphosphate system, with convergence scaling as <span class="katex-eq" data-katex-display="false">1/Nζ1/\sqrt{N\_{\zeta}}</span> and demonstrated across varying FCS sizes and occupied single-particle states. — The stochastic cluster expansion method accurately calculates the total correlation energy of a solvated sodium metaphosphate system, with convergence scaling as $1/Nζ1/\sqrt{N\_{\zeta}}$ and demonstrated across varying FCS sizes and occupied single-particle states.

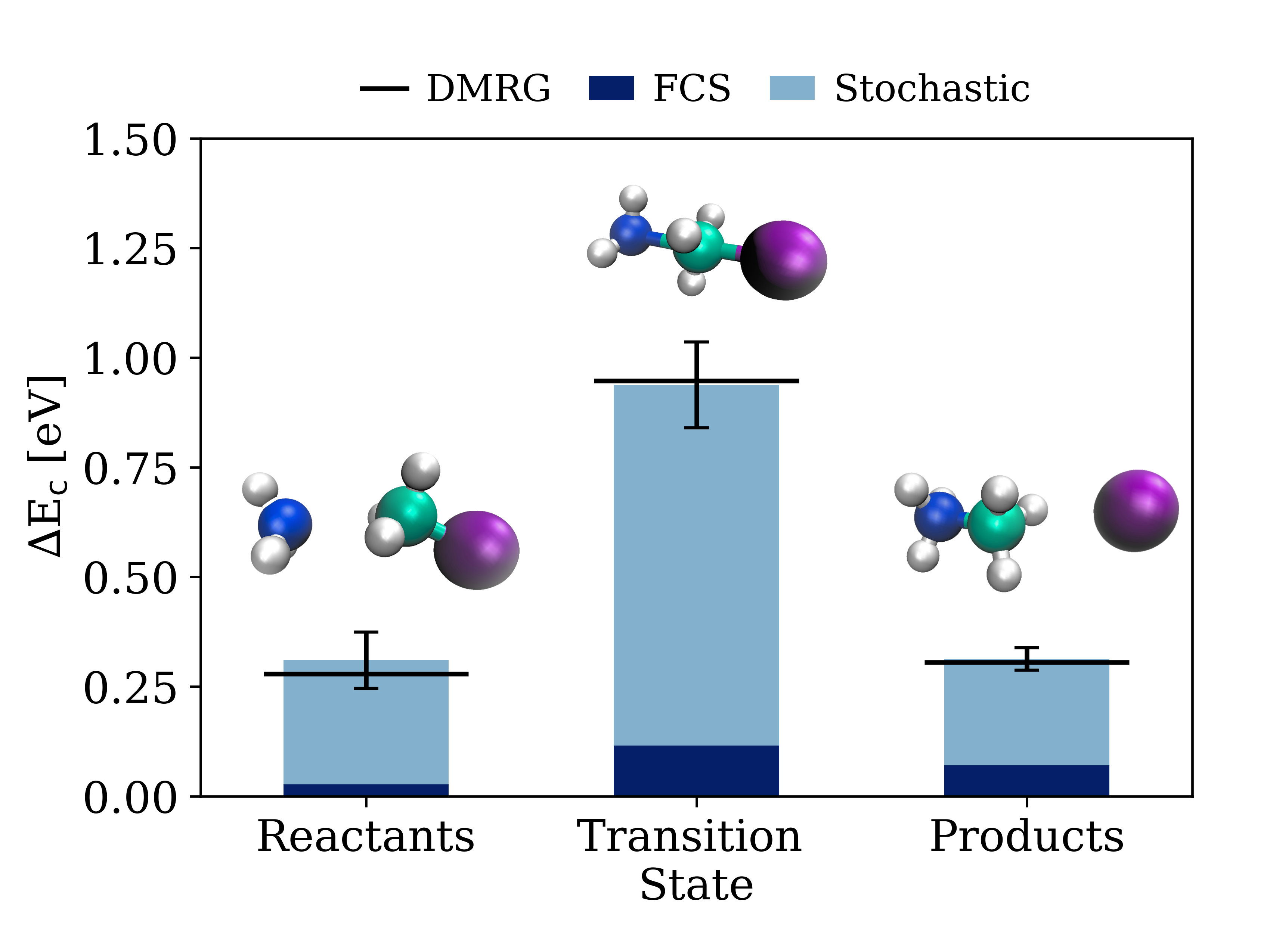
A Benchmark Reaction: Validating Accuracy with the Menshutkin Process

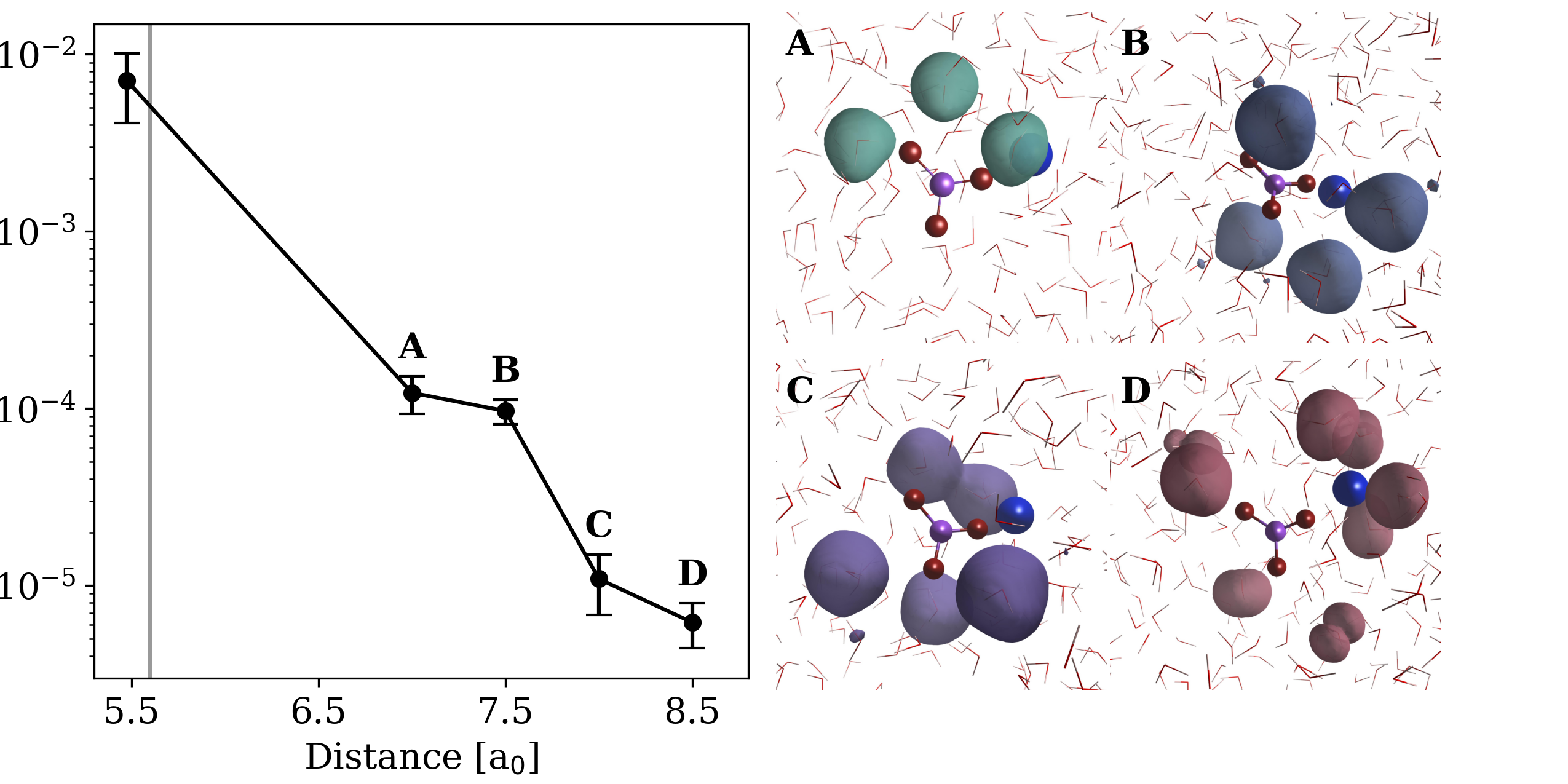
The Menshutkin reaction, a simple yet fundamental chemical process involving the interaction of methyl chloride ( $CH_3Cl$ ) and ammonia ( $NH_3$ ), provides a stringent benchmark for assessing the capabilities of the Symmetry-Adapted Cluster-Configuration Interaction (SCE) method. This reaction’s well-defined energetics and relatively small system size allow for high-level theoretical calculations, serving as a critical validation point for new computational techniques. By accurately modeling this reaction, researchers can confidently apply SCE to more complex chemical systems where experimental data is limited or unavailable. The precision achieved with the Menshutkin reaction demonstrates SCE’s ability to reliably predict reaction pathways and understand the underlying interactions governing chemical transformations, ultimately strengthening its utility as a powerful tool in computational chemistry.

The accuracy of the Symmetry-Adapted Cluster-Complete (SCE) method is powerfully demonstrated through its precise calculation of two-body correlation energies within the Menshutkin reaction. Specifically, SCE reliably captures the delicate balance of interactions, registering a correlation term of $0.0072 \pm 0.0040$ eV for metaphosphate, which diminishes to approximately $0.00002$ eV for water molecules positioned around 7 Bohr away. This meticulous accounting for even subtle intermolecular forces is crucial, as it directly impacts the calculated reaction energetics and provides a dependable description of the underlying reaction mechanism, validating the method’s predictive power for similar chemical processes and offering a robust foundation for further computational studies.

Computational efficiency often necessitates the truncation of the cluster expansion, a technique used to approximate complex many-body interactions. However, this simplification introduces inherent approximations that demand careful scrutiny to maintain the accuracy of calculated correlation energies. Researchers have demonstrated that the validity of these truncated expansions is contingent upon achieving consistency with the Density Matrix Renormalization Group (DMRG) – specifically, ensuring that the correlation energy remains within the standard error of the mean (SEM) across diverse Fragment-Centered Symmetry (FCS) partitionings. This rigorous validation process, employing DMRG as a benchmark, confirms the reliability of the approximations and provides confidence in the calculated energetics and mechanistic details of reactions like the Menshutkin reaction, even when using truncated cluster expansions for practical computations.

Beyond Current Limits: Charting a Course for Future Simulations

Simulating the behavior of molecules within complex environments – such as those found in materials science or biological systems – often requires accounting for intricate interactions that traditional computational methods struggle to capture. A promising approach lies in Symmetry-Adapted Cluster Expansion (SCE), particularly when combined with techniques like Pipek-Mezey Wannierization. This pairing allows researchers to construct highly localized orbitals, effectively focusing computational effort on the chemically relevant regions of a system and diminishing the influence of distant, less critical areas. By adaptively tailoring the expansion to respect the underlying symmetries, SCE dramatically improves the efficiency and accuracy of simulations, opening doors to studying larger, more realistic chemical environments and facilitating predictions of material properties or reaction mechanisms previously beyond reach. The method offers a pathway towards more reliable in silico experimentation and design.

Accurate modeling of chemical processes in solution demands a nuanced treatment of solvent effects, and the Mean-Field External Potential (MFEP) emerges as a critical component in achieving this. This potential effectively represents the average electrostatic influence of the surrounding solvent molecules on the solute, sidestepping the computationally prohibitive task of explicitly simulating every solvent particle. By incorporating the MFEP, calculations can approximate the polarization and dielectric response of the solvent, influencing both the energetics and structure of the solute. The success of solution-phase simulations hinges on a precise formulation of the MFEP, demanding careful consideration of its functional form and the appropriate boundary conditions to accurately capture the screening of electrostatic interactions. Further refinement of MFEP methodologies, including advanced polarization models and non-local treatments, promises to significantly enhance the reliability and predictive power of computational chemistry for systems immersed in complex solvent environments.

The future of Stochastic Cluster Expansion (SCE) hinges on refining the computational strategies used to manage its inherent complexity. While SCE provides a robust framework for simulating chemical systems, its applicability is currently limited by the exponential scaling of the cluster expansion with system size. Consequently, ongoing research focuses on developing more efficient algorithms for generating and evaluating these clusters, alongside innovative truncation schemes to discard less important contributions without sacrificing accuracy. These advancements are not merely about faster computation; they represent a pathway towards modeling increasingly complex systems – including those with thousands of atoms and intricate interactions – that are presently beyond the reach of conventional quantum chemical methods. Successfully overcoming these computational hurdles will unlock the full potential of SCE as a predictive tool for materials science, chemistry, and beyond, enabling the accurate simulation of phenomena occurring in realistic, large-scale environments.

The pursuit of electronic structure calculations, as detailed in this work, isn’t simply about refining existing methods, but fundamentally questioning their limitations. This paper’s Stochastic Cluster Expansion (SCE) embodies that spirit, dismantling the conventional approach to correlation energy calculations by embracing stochastic sampling. It echoes Thomas Kuhn’s assertion that, “science does not proceed by discovering absolute truth but by refining existing paradigms.” The SCE doesn’t aim for a perfect solution within a flawed framework; instead, it re-architects the entire approach, accepting a degree of controlled randomness to navigate the complexity of large nanoscale systems and achieve computational savings. This willingness to challenge established methods is not a weakness, but the very engine of progress.

Beyond the Expansion

The Stochastic Cluster Expansion, as presented, feels less like a culmination and more like a controlled demolition of existing computational bottlenecks. The true exploit of comprehension lies not in simply calculating correlation energies with greater efficiency, but in recognizing the inherent limitations of the cluster approximation itself. Future work must confront the question of when, and where, this expansion breaks down – identifying the system characteristics that render it unreliable. Is there a critical density, a particular orbital symmetry, or a specific type of localized defect that consistently undermines its accuracy?

Downfolding, a technique integral to the method, remains a potential source of systematic error. The art lies in selecting the “right” subspace – a deceptively simple premise. The next iteration will inevitably demand a rigorous framework for quantifying the information lost during this reduction, perhaps through a comparison with benchmark results obtained from methods like Density Matrix Renormalization Group, but applied to increasingly larger systems where DMRG becomes intractable.

Ultimately, the power of SCE isn’t in refining the expansion, but in revealing its failure modes. Each limitation exposed, each point of breakdown, offers a deeper insight into the nature of electronic correlation itself. The goal, then, is not perfect calculation, but a complete map of the method’s territory – knowing precisely where it works, and, more importantly, where it does not.

Original article: https://arxiv.org/pdf/2602.12254.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/