Smarter Solvers: Boosting Accuracy in Corrupted Linear Systems

by

Author: Denis Avetisyan

A new iterative method intelligently filters out unreliable data, accelerating and improving the robustness of solutions for linear equations affected by noise and errors.

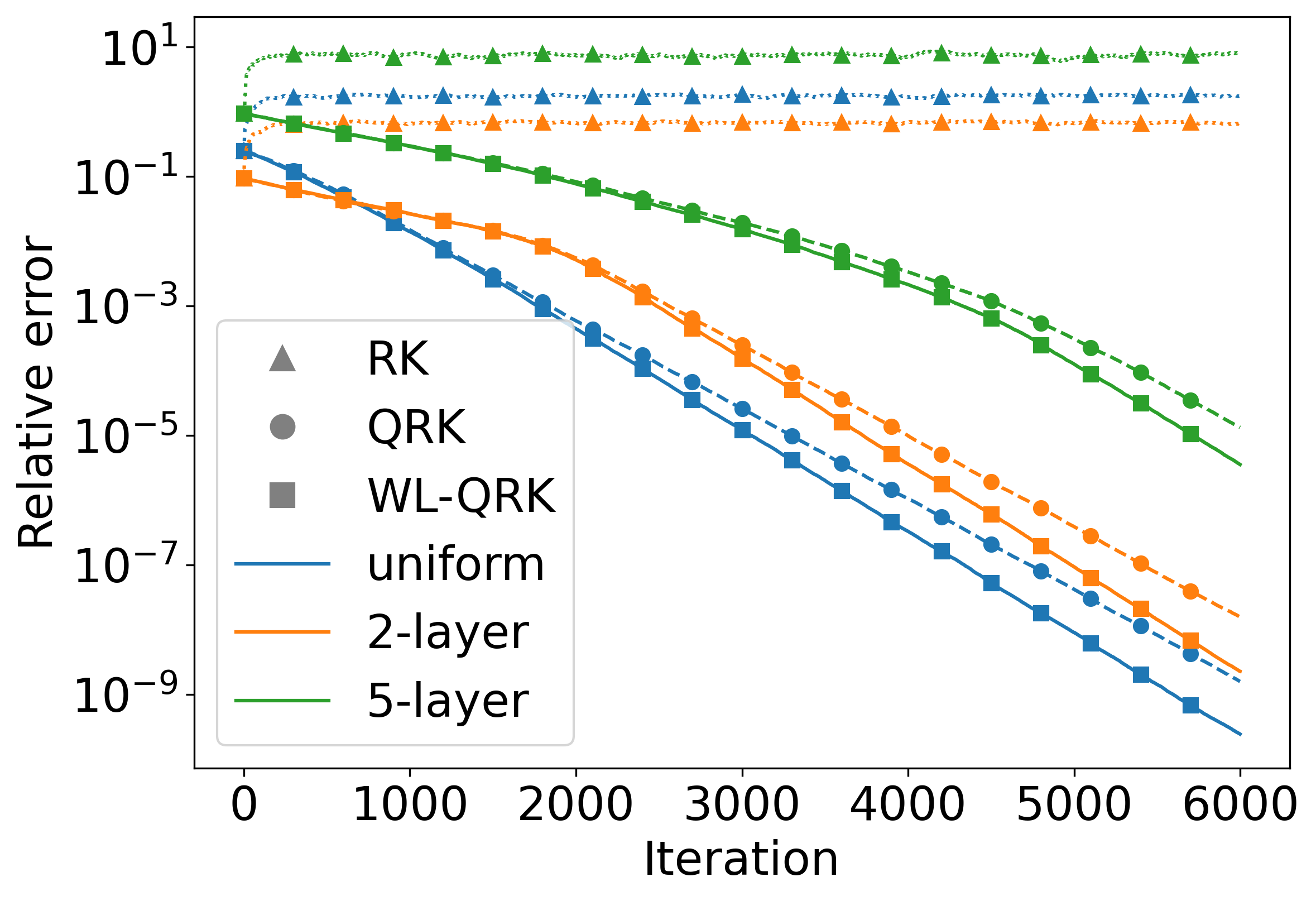
Subsampling with Weighted Least-Squares Quantile Regression Keying (WL-QRK) demonstrates faster convergence than standard Quantile Regression Keying across a range of corruption scenarios, while Regression Keying itself fails to achieve convergence, highlighting the efficacy of weighted approaches in mitigating data degradation.
Subsampling with Weighted Least-Squares Quantile Regression Keying (WL-QRK) demonstrates faster convergence than standard Quantile Regression Keying across a range of corruption scenarios, while Regression Keying itself fails to achieve convergence, highlighting the efficacy of weighted approaches in mitigating data degradation.

This paper introduces WhiteList QuantileRK (WL-QRK), a quantile-based randomized Kaczmarz algorithm with a whitelist trust mechanism for solving large-scale, corrupted linear systems.

While randomized Kaczmarz methods offer rapid solutions to overdetermined linear systems, their sensitivity to noisy data remains a significant challenge. This paper introduces improvements to the {\text{Quantile Randomized Kaczmarz Algorithm with Whitelist Trust Mechanism}}, addressing this fragility through adaptive screening of unreliable equations. Specifically, the authors demonstrate that a novel ‘Whitelist’ mechanism, combined with quantile-based sampling from a small data subset, not only accelerates convergence but also enhances robustness in the presence of corrupted data. Does this adaptive approach represent a viable path towards more reliable and efficient iterative solvers for large-scale, real-world applications?

The Evolving Landscape of Reconstruction: Foundations in Iteration

The reconstruction of images, from medical scans to astronomical observations, frequently hinges on the ability to accurately solve systems of linear equations. These systems arise because image formation can be modeled as a linear process – projections in Computed Tomography (CT), for example, represent linear combinations of the unknown pixel values. Similarly, deblurring an image involves solving for the original, sharp image given blurred observations. The core challenge lies in efficiently determining the values that satisfy these equations, especially when dealing with large datasets – a high-resolution image might contain millions of unknowns. Consequently, the development of robust and computationally efficient methods for solving Ax = b – where A represents the linear operator, x the unknown image, and b the measured data – remains a cornerstone of modern imaging science and data reconstruction techniques.

Introduced in 1937 by Stefan Kaczmarz, the method bearing his name offers a unique iterative solution to the problem of solving systems of linear equations. Rather than directly calculating a solution, the Kaczmarz algorithm progressively refines an initial guess by focusing on satisfying individual equations one at a time. Each iteration projects the current estimate onto the subspace defined by a single equation, gradually converging towards a solution that satisfies all equations simultaneously. This seemingly simple approach, while initially computationally expensive, laid the groundwork for more sophisticated iterative techniques like ART (Algebraic Reconstruction Technique) and other projection-based methods. Its influence extends beyond theoretical mathematics, proving crucial in fields like medical imaging and signal processing where efficiently solving large linear systems is paramount; the Kaczmarz method remains a foundational element in the development of modern data reconstruction algorithms.

Tomography, a cornerstone of modern medical imaging and non-destructive testing, fundamentally relies on the power of efficient linear system solvers to transform raw data into meaningful images. These techniques, such as Computed Tomography (CT) scans, acquire projections – essentially, measurements of an object from multiple angles. Reconstructing a detailed internal image from these projections requires solving a large system of linear equations, where each equation represents a projection and the unknowns are the image’s constituent voxels. The accuracy and speed of this reconstruction are directly tied to the performance of the chosen solver; faster and more precise solvers translate to reduced scan times, lower radiation doses for patients, and higher-resolution images. Consequently, significant research continues to refine these algorithms, striving for computational efficiency and robustness in the face of noisy or incomplete data, enabling advancements in diagnostics and material science.

Whole-leaf quantitative reaction kinetics (WL-QRK) demonstrates improved performance compared to traditional quantitative reaction kinetics (QRK) when analyzing samples using both tomography and white blood cell (WBC) systems.
Whole-leaf quantitative reaction kinetics (WL-QRK) demonstrates improved performance compared to traditional quantitative reaction kinetics (QRK) when analyzing samples using both tomography and white blood cell (WBC) systems.

Navigating Imperfection: Robustness Against Data Corruption

Real-world datasets frequently deviate from the ideal conditions assumed by many linear system solvers. These deviations, termed ‘corruption’, manifest as errors in data measurements or inconsistencies within the system’s defining equations. Such corruption can arise from sensor noise, data transmission errors, or inaccuracies in modeling the underlying physical process. These inconsistencies directly impede the ability of standard solution methods – like least squares – to converge on an accurate solution; even minor errors can lead to significant inaccuracies or complete failure to converge, particularly in overdetermined or ill-conditioned systems. The presence of corruption necessitates the use of more robust algorithms capable of mitigating the impact of these data imperfections and providing reliable solutions despite the presence of noise or inconsistencies in the linear system Ax = b.

The original Kaczmarz algorithm, while guaranteed to converge to a least-squares solution for consistent linear systems, exhibits a linear rate of convergence. Randomized Kaczmarz significantly improves upon this by achieving exponential convergence. This acceleration is achieved through a probabilistic update scheme where rows of the linear system Ax = b are selected with a probability proportional to ||A^T x - b||^2. This stochastic approach, while not altering the eventual solution, dramatically reduces the number of iterations required to reach a desired level of accuracy, particularly for large-scale and high-dimensional problems. The convergence rate is formally demonstrated to be O(1/\epsilon) where Δ is the desired accuracy, representing a substantial improvement over the original algorithm’s linear convergence.

Quantile Randomized Kaczmarz enhances robustness to data corruption by incorporating an acceptance test predicated on a quantile threshold. This test operates by comparing the residual ||A\mathbf{x} - \mathbf{b}|| for a given data point to a dynamically adjusted quantile of previously observed residuals. If the residual exceeds this threshold – indicating a potentially erroneous data point – the update step is rejected. This selective acceptance strategy effectively mitigates the influence of sparse corruptions, preventing the algorithm from being unduly skewed by outliers or inconsistent measurements within the linear system A\mathbf{x} = \mathbf{b}.

Quantile Randomized Kaczmarz enhances solution accuracy in the presence of data corruption by implementing a selective update mechanism. Rather than applying every computed update to the solution vector, the method employs a quantile-based acceptance test; updates are only accepted if their corresponding residual falls below a predetermined quantile threshold. This threshold effectively filters out updates originating from erroneous or inconsistent data points, preventing their disproportionate influence on the overall solution. By focusing on updates representing consistently valid data, the method demonstrates improved robustness and avoids being led towards inaccurate solutions by outliers or corrupted measurements within the linear system.

Subsample WL-QRK achieves comparable performance to full-sample WL-QRK, with its effectiveness in mitigating corruption increasing alongside the number of blocking cycles.
Subsample WL-QRK achieves comparable performance to full-sample WL-QRK, with its effectiveness in mitigating corruption increasing alongside the number of blocking cycles.

Refining the Process: Whitelists, Blocklists, and Adaptive Sampling

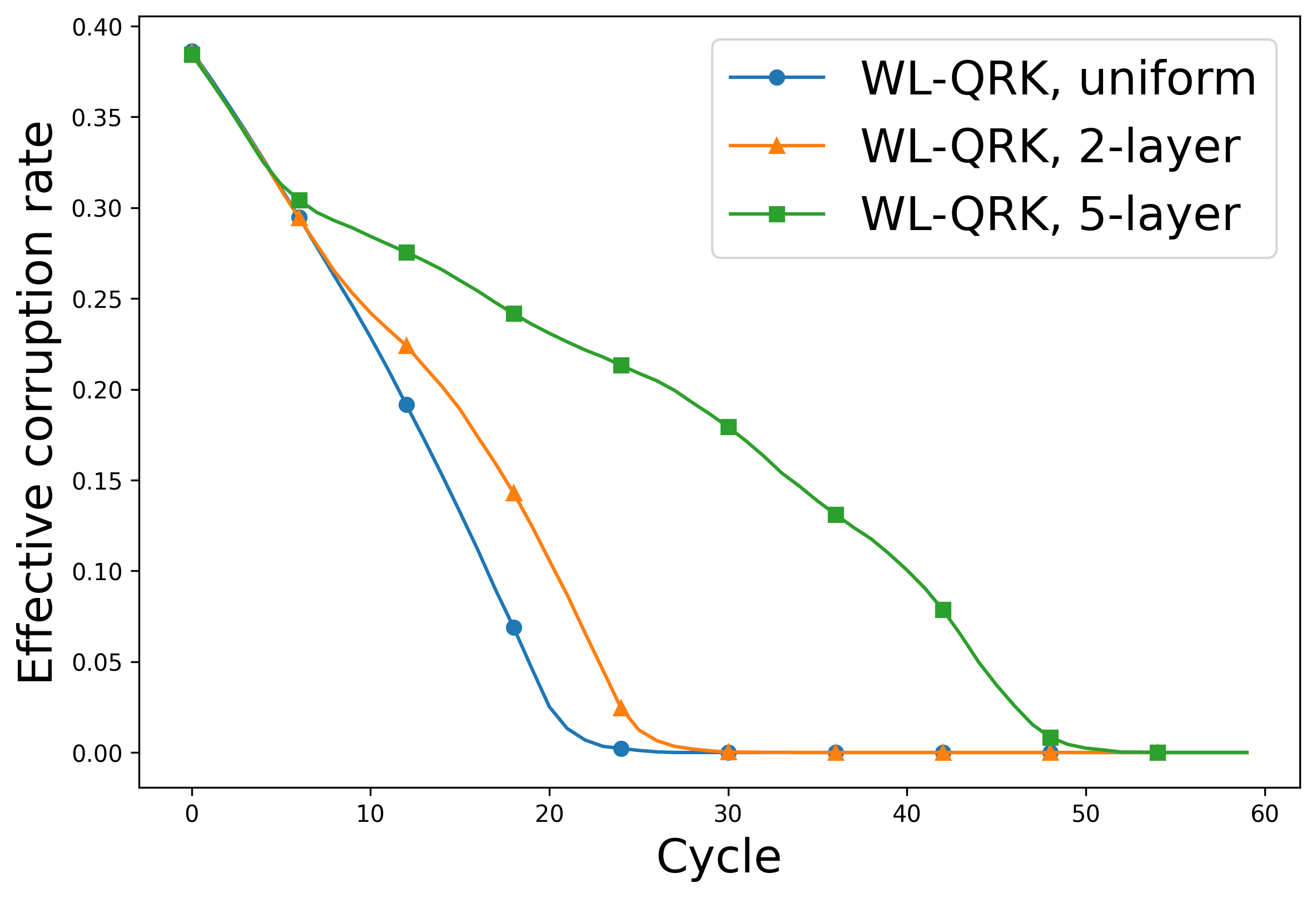
WhiteList Quantile Randomized Kaczmarz (WL-QRK) incorporates dynamic data management through the use of whitelists and blocklists. Rows identified as consistently reliable, indicated by small residuals during iterative updates, are added to the whitelist, effectively prioritizing their contribution to subsequent calculations. Conversely, rows exhibiting persistently large residuals, suggesting potential corruption or inaccuracy, are placed on a blocklist and temporarily excluded from the iterative update process. This mechanism allows the algorithm to focus computational resources on more reliable data points while mitigating the influence of potentially erroneous data, thereby improving the overall robustness and convergence speed of the Randomized Kaczmarz algorithm.

The WhiteList Quantile Randomized Kaczmarz (WL-QRK) algorithm incorporates a whitelist to prioritize data rows exhibiting consistent reliability throughout the iterative solution process. Rows are added to this whitelist based on their demonstrated low residual values across multiple iterations. Inclusion on the whitelist confers preferential treatment; these rows receive increased sampling probability during each update step, effectively accelerating convergence. This prioritization is based on the assumption that consistently reliable data points contribute more effectively to accurate model refinement and can therefore be leveraged to improve the overall efficiency of the algorithm.

The WhiteList Quantile Randomized Kaczmarz (WL-QRK) algorithm employs a blocklist mechanism to address data corruption by temporarily excluding rows exhibiting consistently high residuals. These residuals, representing the difference between predicted and actual values, indicate unreliable data points. Rows exceeding a predetermined residual threshold are added to the blocklist, preventing their participation in iterative updates during that specific iteration. This exclusion serves to mitigate the influence of potentially erroneous data on the overall model convergence, allowing the algorithm to focus on refining the model with more reliable data before re-evaluating previously blocked rows in subsequent iterations.

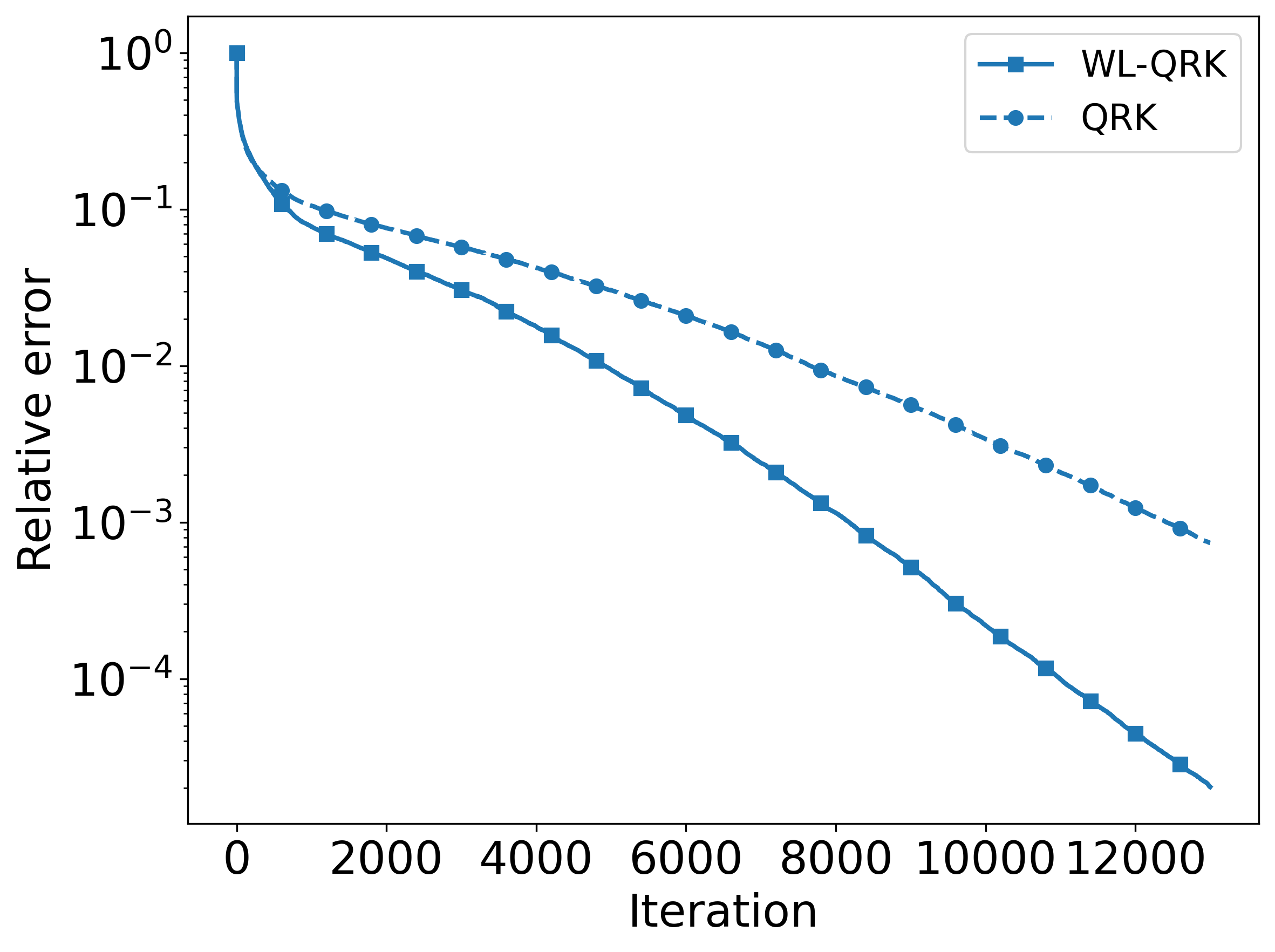
The WhiteList Quantile Randomized Kaczmarz (WL-QRK) algorithm utilizes an adaptive sampling strategy employing both a quantile and a blocking threshold to enhance convergence speed. Empirical evaluations demonstrate that WL-QRK consistently outperforms the standard QRK algorithm, with performance gains becoming more pronounced as the proportion of corrupted data decreases. Specifically, tests on the Tomography dataset, containing approximately 18% corrupted rows, and the WBC dataset, with roughly 25% corruption, showed significant improvements in convergence rates when using the adaptive sampling approach compared to traditional QRK implementations.

Analysis of the Tomography and WBC datasets revealed substantial data corruption rates, with approximately 18% of rows in the Tomography dataset and 25% in the WBC dataset identified as containing errors. These findings demonstrate the practical applicability of the WhiteList Quantile Randomized Kaczmarz (WL-QRK) method in scenarios involving significant data inaccuracies. The method’s ability to effectively manage and mitigate the impact of these corrupted rows contributes to improved convergence and overall solution accuracy, as evidenced by its performance gains over standard QRK implementations in datasets with these levels of corruption.

Expanding the Horizon: Toward Broader Application and Optimization

To accelerate large-scale linear system solutions, variations of the Randomized Kaczmarz algorithm, such as Subsampled Quantile Randomized Kaczmarz, strategically reduce computational cost per iteration. These methods achieve efficiency by estimating the residual quantile-a key metric for determining step size-not from the entirety of the data, but from a randomly selected subset of rows. This subsampling dramatically lowers the per-iteration expense without substantially compromising accuracy, as the quantile can be reliably approximated from a representative sample. The technique effectively balances computational demands with convergence speed, making it particularly valuable when dealing with high-dimensional datasets where full-data processing would be prohibitively expensive. This approach opens possibilities for real-time applications and expands the applicability of Kaczmarz-type algorithms to larger and more complex problems.

Combining adaptive selection strategies with the Kaczmarz algorithm represents a significant refinement in solving linear systems. This approach moves beyond uniform sampling by intelligently prioritizing measurements that contribute most to the convergence process. Instead of treating all data points equally, the algorithm dynamically focuses on those providing the most informative residuals – those that reveal the greatest discrepancy between the current estimate and the true solution. By concentrating computational effort on these crucial data points, the method accelerates convergence and improves overall performance, especially when dealing with high-dimensional or redundant datasets. This selective approach doesn’t simply reduce computational load; it actively enhances the quality of each iteration, leading to a more efficient and robust solution process.

A refinement of the Randomized Kaczmarz algorithm introduces a method for detecting potentially unreliable data contributors within a distributed system. By analyzing the aggregated statistics derived from multiple workers solving the same system of equations, the algorithm can identify inconsistencies indicative of adversarial behavior – instances where a worker intentionally provides inaccurate or misleading information. This approach doesn’t rely on prior knowledge of which workers might be compromised; instead, it leverages the collective behavior of the system itself to flag anomalies. The core principle hinges on the expectation that honest workers will, on average, contribute to a consistent solution, while malicious actors will introduce deviations detectable through statistical analysis of the aggregated results, thus enhancing the robustness of distributed computations.

Recent validation of these randomized Kaczmarz methods, notably using the Wisconsin Breast Cancer Dataset, suggests broad applicability beyond theoretical efficiency. Studies demonstrate the potential for significant acceleration in fields like medical imaging and large-scale machine learning tasks. Importantly, performance isn’t substantially compromised by reducing the dataset size; researchers have found that subsampling to just 40% of the original data yields minimal impact on the convergence rate, while dramatically lowering computational costs. This scalability is crucial for tackling complex, high-dimensional problems where traditional iterative methods become prohibitively expensive, opening doors to real-time analysis and deployment in resource-constrained environments.

The pursuit of iterative solutions, as demonstrated by WhiteList QuantileRK, inevitably contends with the decay inherent in any system. Each iteration, while striving for convergence, operates within a landscape of potentially corrupted data-a form of entropy. This work acknowledges that improvements, like faster convergence rates, are transient; the system’s robustness is constantly challenged by the noise it attempts to overcome. As James Maxwell observed, “The science of the absolutely necessary is a branch of the science of the possible.” This holds true; WL-QRK doesn’t eliminate corruption, but rather manages its impact, acknowledging that even the most refined algorithms exist within a framework of inherent uncertainty and eventual degradation. The method’s adaptive screening represents not a triumph over decay, but a sophisticated accommodation of it.

What’s Next?

The introduction of WhiteList QuantileRK represents a predictable, yet necessary, stage in the evolution of iterative solvers. Versioning, in this context, isn’t merely about improving performance; it’s a form of memory. Each refinement-each iteration toward robustness-acknowledges the inherent decay of any system when confronted with real-world data. The algorithm’s success in navigating corrupted linear systems doesn’t solve the problem of noise, it delays the inevitable entropic increase. The arrow of time always points toward refactoring.

Future work will undoubtedly focus on adaptive whitelist thresholds – determining when an equation’s reliability has degraded beyond salvage. But a deeper question remains: how does one model ‘trust’ itself? The current mechanism relies on observed residuals, a reactive measure. A truly resilient system might anticipate corruption, employing predictive models of equation drift-essentially, building a self-aware solver. This shifts the focus from reacting to noise to anticipating it, a conceptually more elegant, though exponentially more difficult, undertaking.

Ultimately, the pursuit of robust solvers isn’t about achieving perfection-a static, unattainable ideal. It’s about gracefully managing imperfection, extending the lifespan of a functional system in the face of constant degradation. The true metric isn’t convergence speed, but the rate of decay-how long can a solution remain viable before entropy claims it?

Original article: https://arxiv.org/pdf/2602.12483.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

See also:

2026-02-16 07:32