Author: Denis Avetisyan
New research leverages holographic duality to explore the subtle interplay between quantum criticality and entanglement in materials undergoing a transition between superconducting and insulating states.
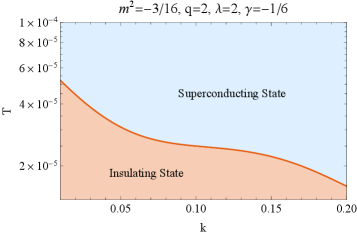
This study demonstrates a novel approach to characterizing phase transitions using mixed-state entanglement measures like the Entanglement Wedge Cross-Section in a holographic p-wave superconductor model.
Understanding the interplay between quantum criticality and entanglement remains a central challenge in condensed matter physics. This is addressed in ‘Quantum criticality and mixed-state entanglement in holographic superconductor–insulator transitions’, where we investigate a holographic model undergoing a superconducting-insulator transition and its associated quantum phase transition. Our results demonstrate that the entanglement wedge cross-section-a measure of mixed-state entanglement-provides a robust diagnostic of this transition, surpassing the limitations of holographic entanglement entropy. Could this approach reveal universal features of quantum criticality in strongly correlated systems beyond the scope of traditional probes?
The Inevitable Bloom of Criticality
Quantum criticality describes the fascinating behavior of materials as they undergo phase transitions-shifts in their physical properties-driven not by thermal fluctuations, but by quantum mechanics. Unlike classical transitions involving heat, these transitions occur at absolute zero temperature, governed by the interplay of quantum entanglement and strong electron correlations. However, pinpointing and characterizing these critical points proves remarkably difficult. The very correlations that define quantum criticality also frustrate traditional theoretical approaches and experimental techniques, often obscuring the underlying physics. This complexity makes quantum criticality a central, yet stubbornly challenging, frontier in condensed matter physics, promising a deeper understanding of material behavior and potentially paving the way for the design of materials with unprecedented properties.
The behavior of materials undergoing quantum phase transitions presents a significant challenge to conventional analytical techniques. These transitions, occurring at absolute zero temperature, are governed by quantum fluctuations and give rise to strong correlations between electrons – interactions that extend far beyond the reach of simple, mean-field approximations. Traditional methods, such as perturbation theory, often break down because these correlations are not weak enough to be treated as minor disturbances. Consequently, a complete description of the system necessitates accounting for these intricate many-body effects, demanding computationally intensive simulations or entirely new theoretical frameworks. This inability to fully capture these correlations hinders a comprehensive understanding of quantum criticality, impeding progress in predicting and designing materials with novel and potentially revolutionary properties.
Progress in understanding strongly correlated systems hinges on developing diagnostic tools and theoretical frameworks capable of navigating their inherent complexity. These materials, where electron interactions dominate, exhibit behaviors that defy traditional condensed matter descriptions, necessitating new approaches to probe their properties. Researchers are actively pursuing methods beyond conventional band theory, including quantum Monte Carlo simulations, dynamical mean-field theory, and sophisticated experimental techniques like angle-resolved photoemission spectroscopy and resonant inelastic x-ray scattering. The goal is to accurately map out the phase diagrams of these systems, identify the critical points governing transitions between different states, and ultimately, predict and control the emergence of novel phenomena-potentially unlocking materials with unprecedented functionalities in areas like superconductivity and quantum computation. Establishing a robust theoretical foundation coupled with reliable experimental validation remains paramount for unraveling the mysteries at the heart of strong correlations.
The ability to manipulate materials at quantum critical points promises a revolution in materials science. These transitions, occurring at the cusp of different phases, allow for the fine-tuning of a material’s electronic and magnetic properties with unprecedented control. Researchers envision designing materials exhibiting enhanced superconductivity, optimized catalytic activity, or entirely novel electronic behaviors – properties unattainable in conventional substances. By understanding and harnessing the physics of these transitions, scientists aim to create materials specifically tailored for advanced technologies, ranging from more efficient energy storage and transmission to next-generation computing and sensing devices. This control isn’t simply about achieving better performance; it’s about realizing functionalities previously considered impossible, opening doors to materials with properties dictated by fundamental quantum principles.
Mapping Complexity with Holographic Shadows
Holographic duality, also known as the AdS/CFT correspondence, proposes a mathematical equivalence between gravitational theories in Anti-de Sitter (AdS) space and conformal field theories (CFT) residing on the AdS boundary. This mapping is particularly useful for strongly correlated quantum systems, where traditional perturbative methods fail due to intractable interactions. The duality allows for the translation of strong coupling problems in the quantum system to a weakly coupled gravitational description, and vice versa. This enables calculations of quantum properties, such as correlation functions and thermal properties, using classical gravitational techniques. The dimensionality of the systems is also related; a d-dimensional CFT is dual to a d+1-dimensional gravitational theory. This correspondence isn’t a physical statement about the universe, but rather a powerful mathematical tool for studying quantum systems.
Holographic duality enables the calculation of properties for strongly correlated quantum systems by reformulating the problem in terms of a corresponding classical gravitational theory. This is advantageous because many-body quantum calculations, which determine the behavior of interacting quantum particles, scale exponentially with system size, making them computationally intractable for all but the simplest systems. By utilizing the duality, certain quantum mechanical observables can be mapped to geometric quantities, such as areas or volumes, within the gravitational dual. These geometric quantities are often significantly easier to compute, offering an alternative pathway to determine the properties of the original quantum system without directly solving the complex many-body problem. Specifically, quantities like correlation functions and transport coefficients can be extracted from the behavior of objects in the gravitational theory, effectively circumventing the computational bottlenecks of traditional quantum methods.
Holographic Entanglement Entropy (HEE) provides a method for characterizing quantum phase transitions through geometrical calculations. The Ryu-Takayanagi formula establishes that the entanglement entropy of a region R in a conformal field theory can be computed from the area A(\partial R) of the minimal surface \partial R in the corresponding Anti-de Sitter (AdS) spacetime that bounds the region R. Changes in the geometry of these minimal surfaces, particularly their area, serve as an order parameter for the quantum phase transition occurring in the boundary field theory. Specifically, divergences in HEE at critical points, and its behavior as the minimal surface changes topology, signal transitions between different phases of matter. This geometrical approach offers a powerful tool to study strongly correlated systems where traditional methods fail.
Conventional methods for analyzing strongly correlated quantum systems frequently encounter limitations due to the exponential scaling of computational complexity with system size. Holographic duality circumvents these challenges by providing access to information regarding quantum systems through their gravitational counterparts, often simplifying calculations and enabling the study of regimes previously intractable. Specifically, properties like correlation functions and entanglement measures, which are computationally expensive to determine directly in the quantum system, can be extracted from geometric quantities calculated in the dual gravitational theory. This approach allows for investigations of phenomena such as non-Fermi liquid behavior and quantum phase transitions that are difficult or impossible to model using traditional many-body techniques, offering insights into the collective behavior of quantum matter beyond the reach of perturbative or mean-field approximations.

Witnessing Criticality Through Emergent Gravity
The Einstein-Maxwell-Dilaton-Axion (EMDA) model represents an advancement in the application of holographic duality – specifically, the Anti-de Sitter/Conformal Field Theory (AdS/CFT) correspondence – to the study of strongly correlated systems undergoing quantum phase transitions. This model extends the standard holographic framework by incorporating several key features necessary to describe quantum criticality, namely, a gravitational background incorporating an Einstein gravity term, an electromagnetic field described by Maxwell’s equations, a scalar field representing the dilaton, and an axion field. The inclusion of these fields allows the EMDA model to effectively simulate the behavior of strongly interacting systems at critical points, where fluctuations become dominant and conventional perturbative methods fail. Critically, the model predicts the emergence of dynamical gravity in the boundary field theory, linking the geometry of the bulk spacetime to the critical phenomena observed in the lower-dimensional quantum system.
The Einstein-Maxwell-Dilaton-Axion model successfully reproduces key characteristics of superconducting transitions, including the emergence of a superconducting gap and associated critical behavior. This is achieved through the model’s ability to simulate strongly correlated electron systems, where conventional methods often fail. Consequently, the model functions as a valuable theoretical framework for investigating quantum phase diagrams – graphical representations of the different phases of matter as a function of parameters like temperature and magnetic field. Specifically, the model allows researchers to map out the regions of stability for the superconducting phase and analyze the transitions between superconducting and normal metallic states, offering insights into the underlying mechanisms governing these phenomena.
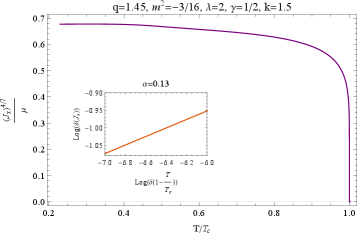
Researchers utilizing the Einstein-Maxwell-Dilaton-Axion model have identified a quantum phase transition exhibiting a scaling exponent of 0.7 for the superconducting gap. This exponent, denoted as ν, dictates how the coherence length – a measure of the spatial extent of superconductivity – diverges as the critical temperature is approached. A value of \nu \approx 0.7 deviates from the mean-field prediction of \nu = 0.5 , indicating strong fluctuations and non-classical critical behavior. The determination of this scaling exponent provides a quantitative characterization of the quantum phase transition and serves as a key parameter for comparison with other theoretical models and experimental observations of superconducting materials.
Calculations of the Entanglement Wedge Cross-Section (EWCS) corroborate the observation of a scaling exponent of 0.7 in the superconducting gap, strengthening the evidence for a quantum phase transition. The EWCS, a geometrical measure derived from holographic duality, directly relates to the entanglement entropy of the boundary conformal field theory. Agreement between the scaling exponent determined from the superconducting gap and that obtained from EWCS calculations provides a consistency check, validating the holographic model’s ability to describe the quantum critical behavior. Discrepancies would indicate inconsistencies in the holographic mapping or the underlying assumptions of the model; the observed consistency, therefore, supports the existence of a quantum phase transition at the critical point.
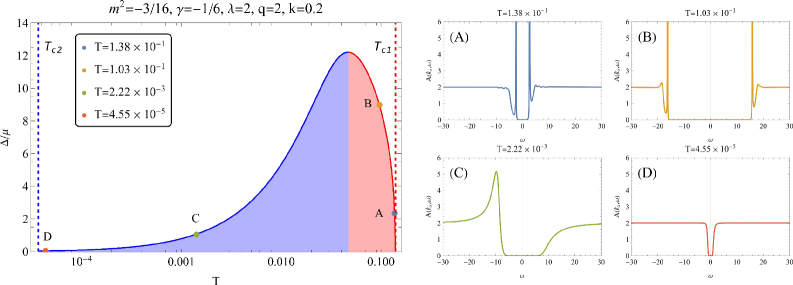
Entanglement as the Shadow of Quantum Order
Characterizing quantum phases and transitions requires a deep understanding of entanglement, the uniquely quantum correlation between particles. While traditional measures like entanglement entropy prove useful for pure quantum states, they often fall short when dealing with the mixed states frequently encountered in realistic physical systems. Mixed states, arising from interactions with an environment or thermal effects, introduce classical correlations that can obscure the underlying quantum entanglement. Consequently, accurately identifying and quantifying entanglement in these complex scenarios becomes crucial for discerning true quantum phase transitions from those driven by classical fluctuations. A complete description demands tools capable of isolating and measuring the quantum correlations present within mixed states, allowing researchers to map out the behavior of matter under extreme conditions and potentially unlock new quantum technologies.
Characterizing entanglement in quantum systems extends beyond pure states, necessitating tools capable of quantifying correlations in mixed states – those representing statistical ensembles of quantum possibilities. Traditional measures like entanglement entropy often prove inadequate for these scenarios; therefore, researchers have turned to quantifiers specifically designed for mixed states, notably entanglement of purification and logarithmic negativity. Entanglement of purification assesses how much entanglement is present in an extension of the mixed state to a pure state, while logarithmic negativity focuses on detecting entanglement even when it’s hidden from certain entanglement witnesses. These approaches provide a more complete picture of quantum correlations, revealing entanglement that would otherwise remain obscured, and are crucial for understanding complex quantum phenomena and phases of matter where mixed states are prevalent.
The holographic principle offers a unique pathway to quantifying entanglement in complex quantum systems through the Entanglement Wedge Cross-Section (EWCS). This approach leverages the duality between gravity in a higher-dimensional spacetime and quantum field theories on its boundary, allowing researchers to translate the problem of calculating entanglement into a geometric one. The EWCS is computed by finding the minimal surface in the higher-dimensional spacetime that connects the entanglement wedge – a region of spacetime causally connected to the entangled system – to its complement. Crucially, this geometric construction provides a concrete way to calculate mixed-state entanglement measures, like entanglement of purification and logarithmic negativity, which are notoriously difficult to compute directly. By relating entanglement to the area of this minimal surface, the EWCS offers both an intuitive geometric interpretation and a practical method for quantifying the intricate correlations within complex quantum states, even those far from equilibrium.
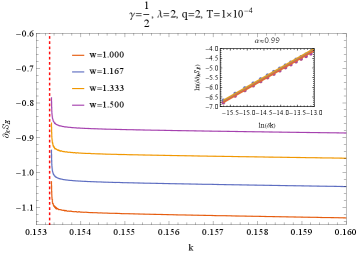
Recent investigations into quantum phase transitions have leveraged the Entanglement Wedge Cross-Section (EWCS) – a geometrically defined measure of entanglement – to provide compelling evidence for a specific transition point. Calculations reveal that the EWCS scales with an exponent of 0.7, a value that strikingly aligns with the known scaling behavior of the superconducting gap – a key indicator of superconductivity. This consistency is not coincidental; the shared scaling exponent strongly suggests a deep connection between entanglement, as quantified by the EWCS, and the emergence of the superconducting phase. The finding offers a novel method for characterizing quantum criticality, moving beyond traditional order parameters and utilizing entanglement as a fundamental diagnostic tool. This validation solidifies the EWCS as a robust probe of quantum entanglement in complex systems and offers a pathway for understanding other exotic quantum phases of matter.
The pursuit of understanding phase transitions, as detailed in this study of holographic superconductivity, feels less like construction and more like observing a garden grow – or, more accurately, wither. The researchers attempt to map the delicate interplay of quantum criticality using measures like the Entanglement Wedge Cross-Section, essentially charting the connections within a complex system as it shifts states. It’s a search for patterns in inevitable decay. As Carl Sagan once observed, ‘Somewhere, something incredible is waiting to be known.’ This work doesn’t build a model of transition; it seeks to understand the inherent logic of these naturally occurring collapses, recognizing that every measurement is merely a snapshot of a fleeting, interconnected reality.
Where Do We Go From Here?
This work, in charting the entanglement landscape of a holographic superconductor-insulator transition, does not so much solve a problem as expose the inevitability of further fracture. The identification of mixed-state entanglement – specifically the Entanglement Wedge Cross-Section – as a diagnostic for a quantum critical point is less a triumph of control, and more an acknowledgement that systems reveal their failings through precisely those metrics most resistant to simplistic interpretation. A system that never breaks is, after all, a system that has ceased to interact with reality.
The reliance on holographic duality, while illuminating, simultaneously underscores the limitations of translating theoretical elegance into experimental verification. The mapping between gravitational degrees of freedom and condensed matter phenomena remains, at best, a suggestive analogy. Future investigations must confront the question of whether these entanglement signatures represent universal features of quantum criticality, or merely artifacts of the chosen theoretical framework. To seek a perfect holographic correspondence is to misunderstand the nature of approximation.
Perhaps the most pressing challenge lies in extending these tools beyond the idealized confines of the model. Real materials are not pristine p-wave superconductors. They are disordered, imperfect, and stubbornly resistant to theoretical neatness. Perfection, in this context, leaves no room for people – or, more accurately, for the complex interplay of interactions that give rise to emergent phenomena. The true test will not be in replicating the model, but in embracing the inevitable deviations.
Original article: https://arxiv.org/pdf/2602.14446.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- Mewgenics Tink Guide (All Upgrades and Rewards)
- One Piece Chapter 1174 Preview: Luffy And Loki Vs Imu
- Top 8 UFC 5 Perks Every Fighter Should Use
- How to Play REANIMAL Co-Op With Friend’s Pass (Local & Online Crossplay)
- How to Discover the Identity of the Royal Robber in The Sims 4
- How to Unlock the Mines in Cookie Run: Kingdom
- Sega Declares $200 Million Write-Off
- Full Mewgenics Soundtrack (Complete Songs List)
- Starsand Island: Treasure Chest Map
- All 100 Substory Locations in Yakuza 0 Director’s Cut
2026-02-17 17:12