Echoes of Quantum Gravity: Ripples in Black Hole Dynamics

Author: Denis Avetisyan

New research explores how quantum effects alter the behavior of charged black holes, potentially leaving observable signatures in their oscillations and thermal emissions.

The behavior of scalar perturbations around a Reissner-Nordström black hole is demonstrably altered by quantum corrections, as evidenced by the variation in the perturbation potential with the quantum correction parameter ζ, specifically when the charge-to-mass ratio is held constant at <span class="katex-eq" data-katex-display="false">Q/M = 1</span>. — The behavior of scalar perturbations around a Reissner-Nordström black hole is demonstrably altered by quantum corrections, as evidenced by the variation in the perturbation potential with the quantum correction parameter ζ, specifically when the charge-to-mass ratio is held constant at $Q/M = 1$ .

This study investigates the impact of quantum corrections on the quasi-normal modes, epicyclic frequencies, and thermodynamic properties of Reissner-Nordström black holes.

Despite the established success of general relativity, a complete understanding of black hole physics requires incorporating quantum effects, particularly in extreme gravitational regimes. This work, ‘Some phenomenological aspects of a quantum-corrected Reissner-Nordström black hole: quasi-periodic oscillations, scalar perturbations and thermal fluctuations’, investigates the phenomenological consequences of a covariant quantum correction to the Reissner-Nordström metric, revealing its impact on dynamical and thermodynamic properties. Specifically, we demonstrate that quantum corrections measurably alter quasi-periodic oscillation radii, scalar perturbation potentials, and black hole entropy, potentially leaving observable imprints on astrophysical data. Could precise measurements of these signatures ultimately constrain the parameters of a quantum gravity theory and refine our understanding of the event horizon?

Unveiling Spacetime: The Classical Foundation of Black Holes

General Relativity posits that Black Holes aren’t simply objects with strong gravity, but rather dramatic distortions of the fabric of spacetime itself. These regions emerge when a sufficiently massive amount of matter is compressed into an extraordinarily small space, creating a gravitational well so intense that nothing, not even light, can escape its pull. The boundary defining this ‘point of no return’ is known as the event horizon. Crucially, it isn’t a physical surface, but a mathematical limit; crossing it represents a one-way journey. The strength of a Black Hole’s gravity is directly proportional to its mass; a more massive Black Hole exerts a correspondingly stronger gravitational influence and possesses a larger event horizon. This theoretical prediction, initially met with skepticism, has since been bolstered by observational evidence, confirming the existence of these enigmatic cosmic entities and solidifying their place as cornerstones of modern astrophysics.

The conventional Newtonian understanding of gravity as a force between masses proves inadequate when considering the extreme conditions around black holes. Instead, Einstein’s theory of General Relativity posits that gravity isn’t a force pulling objects together, but rather a manifestation of the curvature of spacetime itself. Massive objects, like stars and black holes, warp the fabric of spacetime, creating a ‘dip’ that dictates how other objects move within its vicinity. Imagine a bowling ball placed on a stretched rubber sheet; it creates a curve, and any marble rolling nearby will be deflected towards it – this is analogous to how gravity works according to General Relativity. The more massive the object, the greater the curvature, and thus the stronger the gravitational effect. Around a black hole, this curvature becomes infinite at the singularity, creating a region from which nothing, not even light, can escape – a consequence not of a simple attractive force, but of the very geometry of spacetime.

Despite the predictive power of General Relativity in describing Black Holes, a complete understanding remains elusive when considering the extreme conditions at the event horizon. Classical descriptions treat spacetime as a smooth continuum, failing to account for the quantum realm where discrete energy levels and probabilistic behavior dominate. This breakdown is particularly significant near the event horizon, where gravitational forces are immense and quantum effects are theorized to be substantial. Phenomena like Hawking radiation, the emission of particles from Black Holes, are entirely absent from classical calculations, requiring a quantum framework to explain. Consequently, physicists are actively investigating quantum corrections to the classical picture, seeking a more accurate depiction of Black Hole behavior and the fundamental nature of spacetime itself at these extraordinary boundaries.

The purely geometric description of black holes offered by classical general relativity, while remarkably successful, ultimately breaks down at the event horizon due to its neglect of quantum effects. This realization has spurred significant theoretical work investigating potential ‘quantum corrections’ to the classical picture. Researchers posit that quantum gravity, a yet-fully-realized theory, would introduce modifications to spacetime at extremely small scales, potentially altering the black hole’s structure and behavior. These corrections aren’t merely academic exercises; they suggest the event horizon might not be a sharp boundary, but rather a fuzzy, quantum-mechanical region. Furthermore, understanding these quantum effects is crucial for resolving the information paradox – the apparent loss of information as matter falls into a black hole – and for developing a consistent picture of black hole evaporation via Hawking radiation. Consequently, exploration of quantum corrections represents a frontier in theoretical physics, aiming to reconcile general relativity with quantum mechanics and unlock a deeper understanding of these enigmatic cosmic objects.

The product of mass and effective force <span class="katex-eq" data-katex-display="false">M\mathcal{F}</span> scales with dimensionless radial distance <span class="katex-eq" data-katex-display="false">r/M</span> and is modulated by the quantum correction parameter. — The product of mass and effective force $M\mathcal{F}$ scales with dimensionless radial distance $r/M$ and is modulated by the quantum correction parameter.

Quantum Shadows: Correcting Spacetime Geometry

Quantum corrections to the classical spacetime geometry surrounding black holes arise from the application of quantum field theory in curved spacetime. These corrections manifest as deviations from the predictions of general relativity, becoming increasingly significant in the strong gravity regime near the event horizon. Specifically, vacuum fluctuations of quantum fields contribute to the energy-momentum tensor, altering the metric and thus the spacetime geometry. This leads to modifications of the black hole’s properties, including its mass, charge, and angular momentum, and introduces concepts such as Hawking radiation-the emission of particles due to quantum effects near the event horizon-which impacts the black hole’s long-term stability and thermodynamics. The magnitude of these corrections is typically parameterized by terms involving $\hbar$ and curvature scales, indicating their relative importance at different energy levels and proximity to the black hole.

Scalar perturbations, representing disturbances in a scalar field φ propagating in the curved spacetime around a black hole, are a primary method for investigating quantum corrections to classical gravity. These perturbations are mathematically described by the Klein-Gordon equation, a relativistic wave equation for spin-0 particles, modified to account for the black hole’s gravitational field. Specifically, the equation takes the form $( \Box + m^2 )\phi = 0$ , where $\Box$ is the d’Alembert operator in the curved spacetime metric and m represents the mass of the scalar field. Analyzing the solutions to this equation reveals how the curvature of spacetime alters the field’s behavior, and consequently, how quantum effects influence the geometry near the event horizon. The resulting modifications to the classical spacetime structure are directly observable through changes in the propagation and scattering of these scalar perturbations.

Analysis of scalar perturbations around Black Holes demonstrates that quantum effects modify particle and radiation behavior through deviations from classical geodesic motion. Specifically, these perturbations, solutions to the Klein-Gordon equation in a curved spacetime, exhibit backscattering and level splitting not predicted by classical general relativity. The amplitude of backscattered waves, and thus the reflection coefficient, is directly influenced by the quantum corrections to the spacetime metric. Furthermore, the energy levels of particles in the vicinity of the event horizon are shifted due to these quantum corrections, resulting in observable changes to the emitted Hawking radiation spectrum. These alterations indicate a deviation from purely classical behavior and highlight the importance of quantum field theory in curved spacetime for a complete description of Black Hole interactions with matter and energy.

Black Hole thermodynamics and stability are fundamentally linked to the reconciliation of classical General Relativity with quantum field theory. Classical General Relativity predicts singularities at the center of Black Holes, but quantum effects introduce modifications that potentially resolve these singularities and dictate the Black Hole’s temperature and entropy, as described by the Bekenstein-Hawking formula $S = \frac{k_B c^3 A}{4G\hbar}$ , where $S$ is entropy, $k_B$ is Boltzmann’s constant, $c$ is the speed of light, $A$ is the event horizon area, $G$ is the gravitational constant, and $\hbar$ is the reduced Planck constant. These quantum corrections impact the Black Hole’s evaporation rate via Hawking radiation and determine its susceptibility to instabilities, such as those arising from perturbations in the spacetime geometry or the infalling quantum fields. A complete understanding of Black Hole behavior necessitates analyzing this interplay to accurately model their long-term evolution and ensure the consistency of theoretical predictions with potential observational data.

The behavior of squared specific angular momentum and squared specific energy, normalized by mass and expressed as a function of radial coordinate <span class="katex-eq" data-katex-display="false">r/M</span>, demonstrates a dependence on the quantum correction parameter ζ when <span class="katex-eq" data-katex-display="false">Q/M = 1</span>. — The behavior of squared specific angular momentum and squared specific energy, normalized by mass and expressed as a function of radial coordinate $r/M$ , demonstrates a dependence on the quantum correction parameter ζ when $Q/M = 1$ .

Echoes of the Void: Hawking Radiation and Black Hole Evaporation

Hawking radiation originates from the inherent quantum fluctuations in the vacuum of space, particularly pronounced near the event horizon of a black hole. These fluctuations manifest as virtual particle-antiparticle pairs which, due to the extreme gravitational gradient, can be separated. One particle may fall into the black hole while the other escapes as real radiation. This process doesn’t require the black hole to possess any charge or rotation; it’s a consequence of applying quantum field theory in the curved spacetime around a black hole. The emitted particles have a thermal spectrum, with a temperature inversely proportional to the black hole’s mass, meaning smaller black holes emit more intensely and evaporate faster.

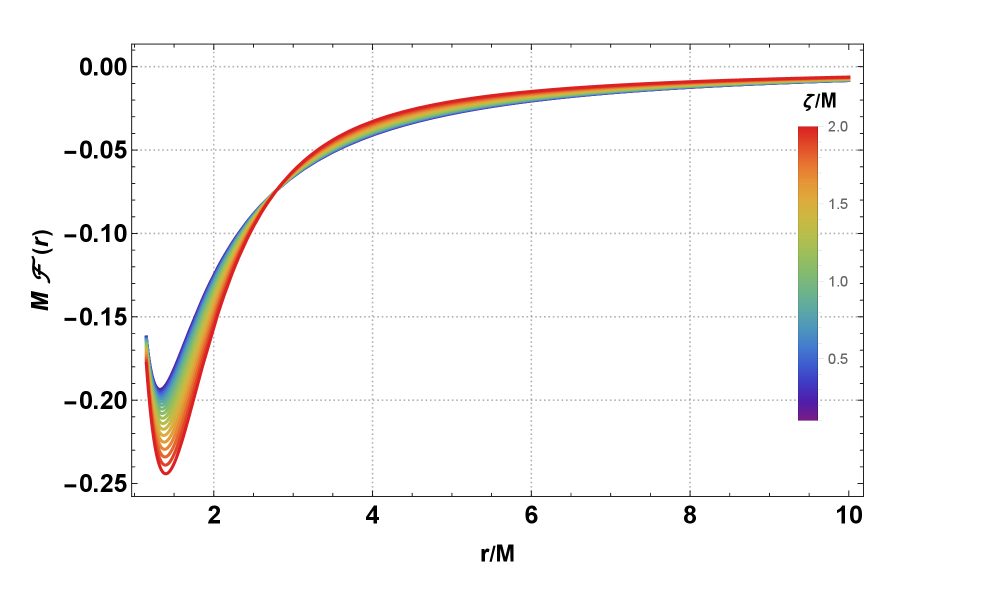
The Greybody Factor is a crucial parameter in calculating the Hawking radiation emission rate from a black hole, representing the probability that an emitted quantum wave is not reflected back due to the black hole’s gravitational potential. This factor is not simply a constant; it is frequency-dependent and varies with the black hole’s mass and spin. Recent calculations demonstrate that the Greybody Factor is affected by a quantum correction parameter, denoted as ζ, which arises from modifications to the black hole’s spacetime geometry at the Planck scale. The inclusion of ζ leads to deviations from the standard semi-classical calculations of the emission rate, potentially altering predictions regarding the final stages of black hole evaporation and impacting the black hole information paradox.

The assertion that black holes are not entirely ‘black’ stems from the prediction of Hawking radiation, whereby quantum effects at the event horizon lead to the emission of particles. This emission constitutes a faint thermal glow with a temperature inversely proportional to the black hole’s mass. Consequently, black holes are not static entities but actively lose mass over time through this radiative process, effectively ‘evaporating’. The rate of evaporation is exceedingly slow for stellar-mass black holes, but becomes significant for hypothetical primordial black holes with sufficiently small masses. This process implies a finite lifespan for black holes, challenging the classical understanding of them as permanent gravitational sinks.

Validating the theoretical prediction of Hawking radiation necessitates a comprehensive understanding of the interaction between quantum field theory and general relativity. Current attempts to reconcile these frameworks are hampered by the lack of experimental evidence directly confirming Hawking radiation, primarily due to the extremely low temperatures and timescales involved. Theoretical progress requires addressing divergences that arise when calculating quantum effects in curved spacetime, often employing techniques like renormalization and regularization. Furthermore, accurately modeling the backreaction of emitted radiation on the black hole’s geometry – a crucial step in understanding the evaporation process – demands solutions to the Einstein field equations coupled with quantum corrections, presenting significant computational and conceptual challenges. The development of a consistent theory of quantum gravity, such as string theory or loop quantum gravity, is considered essential for resolving these issues and providing a robust framework for predicting and verifying Hawking radiation.

The greybody factor for a quantum-corrected Reissner-Nordström black hole decreases with increasing quantum parameter ζ, as demonstrated for <span class="katex-eq" data-katex-display="false">M=1</span>, <span class="katex-eq" data-katex-display="false">Q=0.6M</span>, and <span class="katex-eq" data-katex-display="false">L=2</span>. — The greybody factor for a quantum-corrected Reissner-Nordström black hole decreases with increasing quantum parameter ζ, as demonstrated for $M=1$ , $Q=0.6M$ , and $L=2$ .

Beyond the Horizon: Exotic Black Holes and Their Stability

Black holes, while often depicted as static entities, are subject to the subtle yet pervasive influence of thermal fluctuations. These random deviations from perfect thermodynamic equilibrium arise from the quantum nature of spacetime and impact a black hole’s entropy – a measure of its disorder – and overall stability. The conventional Bekenstein-Hawking entropy, $S = \frac{A}{4G}$ , where $A$ is the event horizon area and $G$ is the gravitational constant, assumes an idealized, unchanging black hole. However, thermal fluctuations introduce corrections to this value, suggesting that the true entropy is more complex and dependent on the black hole’s microscopic state. These fluctuations are particularly important for smaller black holes, where quantum effects are more pronounced, and can even lead to modifications in the event horizon itself, potentially influencing the black hole’s susceptibility to decay or evaporation.

The very fabric of spacetime around a black hole, seemingly defined by a stable event horizon, is subject to subtle disturbances arising from thermal fluctuations. Investigations employing the framework of Euclidean Quantum Gravity allow physicists to probe these quantum effects, revealing that the event horizon isn’t a perfectly rigid boundary but rather a fluctuating entity. This approach treats time as a spatial dimension, facilitating calculations of quantum probabilities and offering a unique perspective on black hole thermodynamics. Through this lens, researchers are uncovering that these fluctuations aren’t merely minor deviations; they contribute to corrections in the calculation of black hole entropy, potentially altering our understanding of how information is encoded and preserved at the horizon. These corrections, while small in many cases, become particularly significant for smaller black holes, indicating a more dynamic and complex structure than previously imagined, and pushing the boundaries of established theories regarding the nature of spacetime itself.

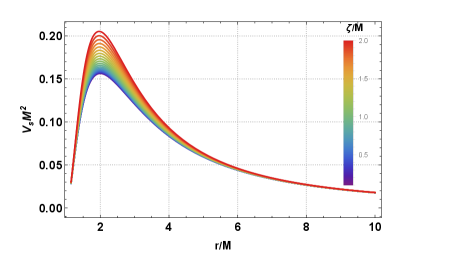
The exploration of Reissner-Nordström black holes, characterized by both mass and electric charge, provides a valuable testing ground for understanding the intricacies of gravity and spacetime. Unlike simpler, uncharged black holes, these objects exhibit a more complex geometry, altering the structure of their event horizons and influencing how they interact with quantum fields. Researchers utilize Effective Potential calculations – a method borrowed from quantum mechanics – to model the behavior of particles around these charged black holes, effectively mapping the gravitational landscape. This approach allows for the investigation of subtle effects, like Hawking radiation and the stability of the horizon itself, revealing how electric charge modifies the standard predictions for black hole thermodynamics and potentially hints at deviations from classical general relativity. These calculations are crucial for building a more complete picture of black hole physics and its connection to other fundamental forces.

Recent investigations into black hole thermodynamics reveals a subtle but significant correction to the standard Bekenstein-Hawking entropy calculation. This correction, expressed as $Sc = S - λ/2 * ln(ST^2)$ , becomes particularly pronounced for black holes characterized by small size and high temperature. The logarithmic term indicates that the conventional entropy formula, while remarkably accurate for macroscopic black holes, begins to falter at the quantum scale. This deviation suggests a more complex relationship between a black hole’s surface area and its internal microstates than previously understood, implying that the number of accessible states is slightly reduced for these smaller systems. Consequently, the logarithmic correction offers a potential window into the quantum gravity effects governing black hole behavior and could be crucial for refining theoretical models that accurately describe these enigmatic objects at the limits of physics.

The effective potential <span class="katex-eq" data-katex-display="false">U_{eff}</span> exhibits distinct behavior as a function of scaled radius <span class="katex-eq" data-katex-display="false">r/M</span> depending on the magnitude of the quantum correction parameter ζ, with <span class="katex-eq" data-katex-display="false">Q/M = 1</span>. — The effective potential $U_{eff}$ exhibits distinct behavior as a function of scaled radius $r/M$ depending on the magnitude of the quantum correction parameter ζ, with $Q/M = 1$ .

Cosmic Echoes: Observational Links Through Quasi-Periodic Oscillations

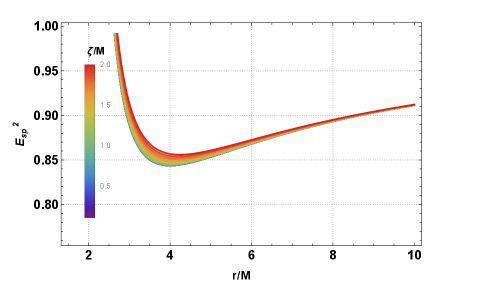
Certain astrophysical systems, such as X-ray binaries and active galactic nuclei, exhibit fascinating phenomena known as Quasi-Periodic Oscillations (QPOs) in their emitted X-ray radiation. These aren’t random fluctuations, but rather discernible, repeating patterns suggesting a dynamic interplay between matter and the immense gravitational forces surrounding a Black Hole. Specifically, the observed frequencies of these oscillations are strongly believed to correlate with the orbital and resonant frequencies of material swirling around the Black Hole’s event horizon. The inner regions of accretion disks, where matter spirals inward, become incredibly hot and emit copious amounts of X-rays; variations in this emission, driven by the orbital motions and interactions within the disk, manifest as QPOs. By meticulously analyzing these frequencies, scientists can effectively map the spacetime geometry very close to the Black Hole, offering a unique window into the most extreme gravitational environments in the universe and testing the predictions of Einstein’s theory of General Relativity.

The swirling accretion disks surrounding black holes don’t simply emit radiation; they vibrate with detectable frequencies known as Quasi-Periodic Oscillations (QPOs). By meticulously analyzing these QPOs through the framework of epicyclic frequency calculations, scientists can effectively map the warped spacetime geometry closest to the black hole’s event horizon. These calculations reveal that the ratios between different QPO frequencies – often appearing as simple fractions like 3:2, 4:3, or 5:4 – aren’t merely coincidental. Instead, these ratios are subtly influenced by a quantum correction parameter, ζ, which arises from modifications to the black hole’s spacetime geometry at the Planck scale. The inclusion of ζ leads to deviations from the standard semi-classical calculations of the emission rate, potentially altering predictions regarding the final stages of black hole evaporation and impacting the black hole information paradox.

Accurately determining the properties of black holes from quasi-periodic oscillations (QPOs) necessitates sophisticated statistical methods, and Markov Chain Monte Carlo (MCMC) analysis has become indispensable in this pursuit. The complexity of models linking QPO frequencies to spacetime geometry requires estimating multiple parameters simultaneously, a task ideally suited to MCMC’s ability to explore high-dimensional parameter spaces. This technique doesn’t simply yield single ‘best-fit’ values; instead, it generates a probability distribution for each parameter, reflecting the uncertainties inherent in the data and model. Consequently, researchers can not only estimate values like the black hole’s spin and the location of the QPO-emitting region, but also rigorously quantify the associated errors. By sampling this posterior distribution, MCMC allows for a robust assessment of model confidence and facilitates meaningful comparisons between theoretical predictions and observational data, ultimately driving advancements in our understanding of these enigmatic celestial objects.

Recent investigations into quasi-periodic oscillations (QPOs) emanating from accreting black holes reveal a compelling connection between theoretical predictions and observational data. Specifically, the normalized radial separation, denoted as $\delta r = r_{QPO}/r_{ISCO} - 1$ ,-which quantifies the distance of the QPO-emitting region from the innermost stable circular orbit-demonstrates a clear inverse relationship with the quantum correction parameter ζ. As the influence of quantum gravity, represented by increasing values of ζ, becomes more pronounced, the calculated radial separation $\delta r$ diminishes. This finding is significant because it provides a measurable signature-a quantifiable decrease in orbital distance-linking the abstract realm of quantum gravity to the observed dynamics of matter swirling around a black hole, offering a potential avenue for empirically testing theories beyond classical general relativity.

A four-dimensional Markov Chain Monte Carlo analysis of Quasi-Periodic Oscillation data constrains the parameters defining the Black Hole within the Quasi-periodic Crustal Ringing Network (QCRN).

The exploration of Reissner-Nordström black holes, particularly with quantum corrections, reveals a complex interplay between geometry and particle behavior. Just as discerning patterns within data demands meticulous examination, so too does understanding these black holes require a careful consideration of their quasi-normal modes and scalar perturbations. As Blaise Pascal noted, “The eloquence of a man does not depend on his voice, but on the thoughts he expresses.” Similarly, the significance of this research lies not merely in the mathematical framework, but in the insights it provides into the fundamental nature of gravity and the universe-a testament to the power of rigorous analysis to illuminate even the most enigmatic phenomena. The study highlights how subtle quantum effects leave observable signatures, enriching our understanding of black hole thermodynamics.

Where Do We Go From Here?

The exploration of quantum corrections to classical black hole solutions, as demonstrated by this work, inevitably reveals the limits of current analytical techniques. The Reissner-Nordström metric, while mathematically tractable, represents a simplification; real astrophysical black holes possess charge and angular momentum in arbitrary ratios. Future investigations must grapple with the increased complexity of the Kerr-Newman spacetime, even if it necessitates embracing numerical relativity or approximation schemes that sacrifice some elegance. Every deviation from idealized solutions, however, is an opportunity to uncover hidden dependencies.

Furthermore, the connection between quasi-normal modes and observed quasi-periodic oscillations remains tantalizingly indirect. While this study illuminates the theoretical pathways through which quantum effects might manifest in the epicyclic frequencies of test particles, discriminating these subtle signatures from astrophysical noise-or from the effects of accreting matter-presents a formidable challenge. The exploration of more realistic accretion disk models, coupled with detailed waveform analysis, will be crucial.

Ultimately, the pursuit of quantum gravity is not merely a quest for a mathematically consistent theory, but a search for a deeper understanding of spacetime itself. The black hole, as a laboratory for extreme physics, continues to offer insights, even-and perhaps especially-in the form of persistent anomalies and unresolved questions. The very persistence of these difficulties suggests that the true nature of gravity lies beyond the reach of current paradigms.

Original article: https://arxiv.org/pdf/2602.15551.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/