Author: Denis Avetisyan
New calculations offer a unified, Poincaré-covariant framework for understanding how quarks fragment into observable mesons, bridging theory with experimental data.
This review presents a calculation of fragmentation functions for light and heavy-light mesons using the Bethe-Salpeter equation, offering insights into hadronization within and beyond Quark-Gluon Plasma.
Understanding how quarks transform into observable hadrons remains a central challenge in quantum chromodynamics, particularly when considering the production of heavy-flavor mesons. This work, ‘Charm and strange meson fragmentation functions’, presents a Poincaré-covariant calculation of fragmentation functions describing this hadronization process for both light and heavy-light mesons, employing a cascade model based on the Bethe-Salpeter equation and coupled jet equations. The resulting fragmentation functions provide a consistent description across different quark flavors, offering a framework for comparing theoretical predictions with experimental data and global analyses. Will this approach pave the way for more accurate modeling of hadron production in high-energy collisions and a deeper understanding of the quark-gluon plasma?
The Allure of Fragmentation: A Quantum Mirror
Quark fragmentation serves as the crucial link between the quantum realm of colliding heavy ions and the macroscopic world of detected particles. When heavy ions collide at near-light speeds, the energy released creates a quark-gluon plasma, a state of matter where quarks and gluons are no longer confined within hadrons. As this plasma expands and cools, quarks subsequently transition into observable hadrons – particles like protons, neutrons, and pions – through a process called fragmentation. Precisely understanding this fragmentation is paramount; the characteristics of the resulting hadrons provide vital clues about the properties of the initial quark-gluon plasma, including its temperature, density, and viscosity. Researchers analyze the abundance, momentum distributions, and correlations of these hadrons to reconstruct the conditions present during the fleeting moments after the collision, effectively using fragmentation as a ‘decoder’ of the plasma’s complex behavior.
The realm of the strong force, governing interactions between quarks and gluons, presents a significant challenge to conventional theoretical approaches. Standard perturbative methods, successful in describing many physical phenomena, falter when applied to the low-energy, nonperturbative regime characteristic of quark fragmentation. This breakdown arises because the strong force becomes, well, strong at these energy scales, rendering the usual approximations invalid. Consequently, physicists require more sophisticated tools-those capable of handling the inherent complexities of these interactions without relying on expansions that simply don’t converge. These advanced techniques, like the Dyson-Schwinger Equation, move beyond approximations to directly calculate the fundamental properties of quarks and gluons, offering a pathway to accurately model the formation of hadrons and understand the behavior of matter under extreme conditions.
The Dyson-Schwinger Equation (DSE) offers a compelling pathway to understanding the strong force by directly calculating the Dressed Quark Propagator – a fundamental object describing the behavior of quarks within hadrons. Unlike traditional perturbative approaches which falter in the realm of strong interactions, the DSE operates within a nonperturbative framework, allowing for accurate modeling of quark dynamics even at extreme energy densities. This equation effectively sums an infinite series of quark self-energy corrections, revealing how interactions modify the quark’s properties – its mass and momentum distribution – as it propagates through the quantum chromodynamics vacuum. The resulting dressed propagator is not simply a quark ‘bare’ mass, but a dynamically generated, effective mass incorporating the influence of the strong force, and is crucial for predicting observable properties of hadrons produced in heavy-ion collisions; it provides a bridge between theoretical calculations and experimental data by providing a realistic depiction of quarks as they fragment into the particles detected in experiments.
Untangling the Interactions: A Path to Hadronization
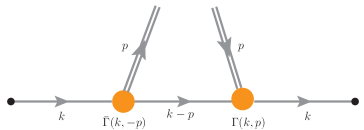
The Bethe-Salpeter Equation (BSE) provides a non-perturbative framework for calculating bound states of two-fermion systems, specifically quark-antiquark pairs, which directly correspond to the formation of hadrons like mesons. Unlike perturbative methods reliant on a small coupling constant, the BSE sums all possible interactions between the quarks, offering a more complete description of their bound state. The equation is an integral equation where the kernel represents the exchanged interactions, and the solution is the Bethe-Salpeter amplitude Γ, which defines the bound state. By solving the BSE with appropriate interaction kernels, one can determine the hadron’s mass, decay constants, and other relevant properties. This approach is crucial for understanding hadron structure from first principles, as it avoids assumptions about potential models and directly addresses the strong interaction dynamics.
The Bethe-Salpeter equation, while capable of calculating hadron bound states, is not solvable in isolation. Its solution fundamentally depends on the Dressed Quark Propagator, which encapsulates the effects of strong force interactions on individual quarks within the hadron. This propagator is itself determined by the Dyson-Schwinger Equation, a non-perturbative equation of motion for the quark field. Consequently, a self-consistent solution requires an iterative process: the Dyson-Schwinger equation provides the Dressed Quark Propagator, which is then used within the Bethe-Salpeter equation to calculate the hadron’s bound state, and the resulting interactions can refine the Dressed Quark Propagator itself. \Gamma(p,q) represents the kernel of the Bethe-Salpeter equation, and its interaction with the Dressed Quark Propagator determines the overall hadron properties.
The Bethe-Salpeter Amplitude, a central result of solving the Bethe-Salpeter equation, functions as a wavefunction describing the correlated state of a quark-antiquark pair forming a meson. Specifically, it details the probability amplitude for finding the quarks at a given separation and with particular relative momentum. Analysis of this amplitude reveals key structural information, including the meson’s size, shape, and internal momentum distribution; these properties are not simply a sum of individual quark characteristics but emerge from the strong interaction binding them. Furthermore, the amplitude’s functional form dictates the meson’s decay constants and other observable quantities, providing a direct link between theoretical calculations and experimental measurements.
Decoding the Cascade: From Quarks to Observable Hadrons
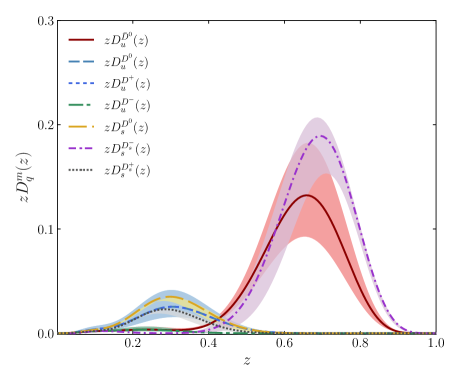
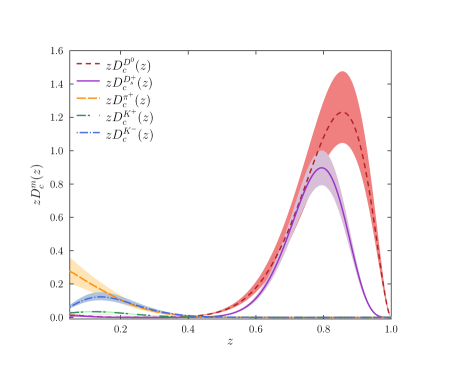
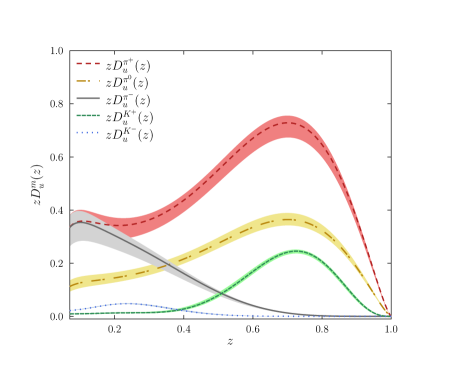
Fragmentation functions (FFs) quantify the probability that a quark produced in a high-energy collision will hadronize into observable particles. These functions are essential for bridging the gap between theoretical calculations, which often deal with quarks and gluons, and experimental measurements that detect hadrons like pseudoscalar mesons (e.g., pions, kaons) and charmed mesons (e.g., D^0, D^+\). Specifically, FFs detail the momentum distribution of the resulting hadrons as a function of the initial quark’s momentum, enabling predictions for experimentally accessible quantities such as hadron production rates in jet events. The accuracy of these functions directly impacts the precision with which theoretical models can be tested against experimental data from facilities like the LHC and future colliders.
The calculation of fragmentation functions necessitates advanced theoretical approaches due to the non-perturbative nature of hadronization. The Bethe-Salpeter Equation, a relativistic equation describing bound states, is employed to model the interactions between quarks and gluons during the fragmentation process, accounting for the complex many-body effects. Furthermore, modeling Jet Cascades – the sequential branching and hadronization of energetic quarks and gluons – is crucial for accurately simulating the evolution from partonic to hadronic states. These cascade models require the solution of coupled differential equations, often employing Monte Carlo techniques, to track the energy and momentum sharing during hadron formation and to determine the final hadron multiplicities and spectra. Accurate implementation of both the Bethe-Salpeter Equation and jet cascade dynamics is essential for reducing theoretical uncertainties and achieving reliable predictions for experimental observables.
This work details a Poincaré-covariant calculation of fragmentation functions, a method ensuring Lorentz invariance in the description of hadron production from fragmenting quarks. The calculated functions demonstrate agreement with existing global analyses, validating the approach against established experimental data. Furthermore, the presented calculation establishes a quantifiable framework for studying the process of quark hadronization, allowing for systematic investigation and comparison of theoretical predictions with experimental observations. This framework relies on well-defined parameters and metrics, enabling precise assessment of the model’s accuracy and predictive power in describing the transition from partonic to hadronic states.
The analysis determined a model scale of 0.63 GeV through comparison with a πN Drell-Yan analysis. This matching process required consideration of the valence quark distribution, which was found to be ⟨x⟩v = 0.47(2). The established model scale is critical for accurately predicting fragmentation functions and ensuring consistency with experimental data derived from high-energy collisions, specifically those involving pion-nucleon interactions as observed in the Drell-Yan process.
The Drell-Levy-Yan (DLY) relation establishes a direct link between fragmentation functions, D(z), and the probability of observing specific hadrons in high-energy collisions. This relation arises from considering the process of hadronization, where quarks and gluons produced in a hard scattering event transform into observable hadrons. Specifically, the DLY relation connects the fragmentation function to the probability of a quark with momentum fraction z producing a hadron, allowing for the calculation of hadron multiplicities and energy distributions in experiments. Its importance stems from providing a theoretical framework to relate theoretical calculations of quark fragmentation to experimentally measurable quantities, facilitating the validation of theoretical models and the extraction of fundamental parameters in high-energy physics.
The Evolving Picture: Scale Dependence and Global Consistency
Fragmentation functions, which describe how energy from a primary particle cascades into secondary particles, are not static entities but rather evolve with the energy scale of the interaction. This scale dependence arises from the fact that at higher energies, more virtual particles can be created, influencing the probability of different fragmentation outcomes. Consequently, a fragmentation function determined at one energy level will not accurately predict behavior at significantly different energies-a critical limitation for precise calculations in particle physics. Addressing this requires a robust theoretical framework capable of extrapolating fragmentation functions across a wide range of energies, ensuring predictions remain consistent with experimental observations and allowing for meaningful comparisons between theoretical models and collider data. Without accounting for this energy dependence, predictions concerning particle production in high-energy collisions would be fundamentally flawed.
The behavior of fragmentation functions-which describe how quarks and gluons transform into observable hadrons-is not static but changes with the energy scale of the interaction. This dependence is systematically understood and calculated through the DGLAP equations, a set of integro-differential equations named after Dokshitzer, Gribov, Lipatov, Altarelli, and Parisi. These equations describe how the distribution of partons within a hadron evolves as the energy scale changes, effectively accounting for the emission of additional partons at higher energies. By solving the DGLAP equations, physicists can predict fragmentation functions at any given energy scale, starting from a known initial condition at a lower scale; this predictive power is essential for accurate modeling of high-energy particle collisions and interpreting experimental results, enabling precise tests of the Standard Model and searches for new physics.
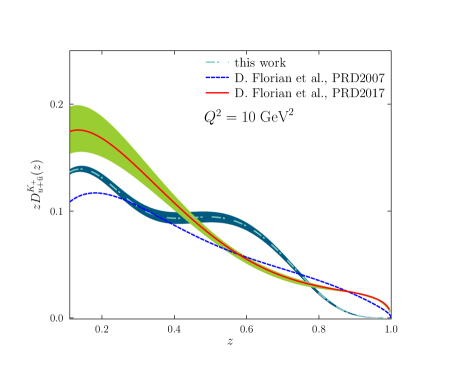
Recent studies have successfully evolved fragmentation functions using the DGLAP evolution equations to an energy scale of 10 GeV². This advancement represents a significant step towards refining predictions in high-energy physics, as fragmentation functions detail how quarks and gluons transform into observable hadrons. The evolved functions exhibit notable agreement with established global analyses – comprehensive studies that combine theoretical frameworks with a wealth of experimental data. This corroboration validates the methodologies employed and underscores the model’s capacity to accurately describe particle production at these energy levels, ultimately enhancing the precision of calculations within the Standard Model and beyond.
The determination of precise fragmentation functions relies heavily on global analysis, a powerful technique that systematically merges theoretical predictions with a wealth of experimental data. This process isn’t simply about fitting a curve; it’s a complex optimization that accounts for the distribution of momentum fraction, x, carried by the fragmenting parton. By incorporating data from diverse experiments – spanning different collision energies and final state particles – global analyses refine the theoretical understanding of how partons transform into observable hadrons. The resulting fragmentation functions aren’t just abstract mathematical constructs; they become essential tools for interpreting high-energy collision events and making accurate predictions for future experiments, effectively bridging the gap between the quantum realm of partons and the macroscopic world of detected particles.
The reliability of any theoretical prediction hinges on the internal consistency of the calculations, and recent work demonstrates a high degree of numerical precision in satisfying fundamental conservation laws. Specifically, the calculated fragmentation functions adhere to both normalization and momentum sum rules – critical checks ensuring that the total probability and momentum are accounted for – with a precision exceeding 99%. This level of accuracy, achieved through rigorous numerical techniques, validates the model’s framework and provides confidence in its predictive power. Maintaining such precision is not merely a technical detail; it’s essential for extracting meaningful insights from experimental data and building a robust understanding of particle fragmentation processes, allowing for more accurate predictions in high-energy physics.
The calculation of fragmentation functions, as detailed in this work, reveals a humbling truth about the foundations of particle physics. It isn’t merely charting the behavior of quarks, but a continuous confrontation with the limits of current understanding. As Francis Bacon observed, “Knowledge is power,” yet this power is perpetually tempered by the realization of how little is truly known. The pursuit of understanding hadronization, especially within the context of quark-gluon plasma, demonstrates this principle acutely; each refined calculation, each favorable comparison to experimental data, brings into sharper focus the vastness of what remains beyond the event horizon of current theory. Everything we call law can dissolve at the event horizon.
Where Do the Fragments Lead?
This calculation of fragmentation functions, though rigorously Poincaré-covariant, represents but a local charting of an immense, turbulent sea. It is a pocket black hole of a model, capable of describing certain hadronic decays with admirable precision, yet ultimately limited by the inherent non-perturbative nature of the strong interaction. The Bethe-Salpeter Equation, while a powerful tool, demands assumptions about confinement and the underlying dynamics that remain stubbornly elusive. One might achieve quantitative agreement with current data, but that agreement should not be mistaken for understanding.
The true challenge lies not in refining these calculations, but in confronting the limitations of the framework itself. To dive into the abyss of full QCD simulations requires computational resources that strain the boundaries of possibility, and even then, the results are susceptible to truncation errors and the ever-present spectre of numerical instability. Perhaps the most fruitful path forward involves a more holistic approach, integrating insights from lattice QCD, effective field theories, and even the seemingly disparate realm of quark-gluon plasma phenomenology.
Sometimes matter behaves as if laughing at established laws, creating particles and correlations that defy simple explanation. To truly map the landscape of hadronization, one must accept that the complete picture may forever remain beyond reach – a humbling realization, but one that fuels continued exploration. The fragments themselves are merely signposts, hinting at a deeper, more complex reality.
Original article: https://arxiv.org/pdf/2602.15694.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- Jujutsu Kaisen Modulo Chapter 23 Preview: Yuji And Maru End Cursed Spirits
- Mewgenics Tink Guide (All Upgrades and Rewards)
- 8 One Piece Characters Who Deserved Better Endings
- Top 8 UFC 5 Perks Every Fighter Should Use
- How to Play REANIMAL Co-Op With Friend’s Pass (Local & Online Crossplay)
- How to Discover the Identity of the Royal Robber in The Sims 4
- Sega Declares $200 Million Write-Off
- How to Unlock & Visit Town Square in Cookie Run: Kingdom
- How to Unlock the Mines in Cookie Run: Kingdom
- Full Mewgenics Soundtrack (Complete Songs List)
2026-02-19 01:12