When Moiré Materials Melt: A New View of Quantum Transitions

Author: Denis Avetisyan

Researchers have mapped the electrical behavior of exotic materials at a critical point, revealing universal properties as they transition between distinct quantum states.

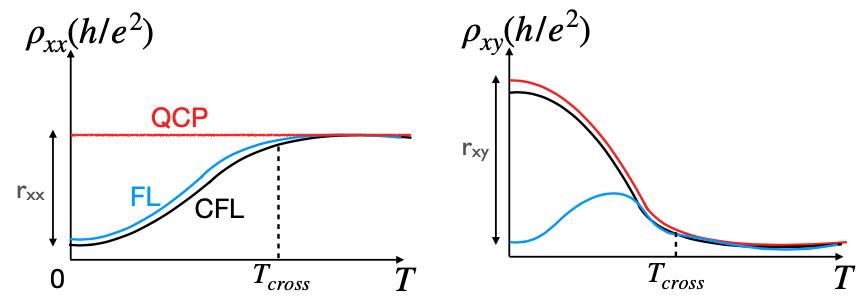
The study demonstrates that resistivity, as a function of temperature, exhibits universal jumps-on the order of <span class="katex-eq" data-katex-display="false">h/e^{2}</span>-at quantum critical points, as evidenced by the distinct behaviors of the fluid limit (blue) and the conformal fluid limit (black) compared to these critical regimes (red). — The study demonstrates that resistivity, as a function of temperature, exhibits universal jumps-on the order of $h/e^{2}$ -at quantum critical points, as evidenced by the distinct behaviors of the fluid limit (blue) and the conformal fluid limit (black) compared to these critical regimes (red).

This review details the predicted d.c. conductivities and experimental signatures near the composite Fermi liquid to metal transition in Moiré Chern bands, informed by Chern-Simons theory and the quantum Boltzmann equation.

Understanding the interplay between strong correlations and topology remains a central challenge in condensed matter physics. This is addressed in ‘Universal electrical transport of composite Fermi liquid to Metal transition in Moiré systems’, which investigates the quantum critical behavior arising at the transition between a composite Fermi liquid and a metal in moiré Chern bands. Through a novel QED-Chern-Simons framework and large- $N$ expansion, we predict universal DC conductivities of approximately $0.033e^2/\hbar$ and $0.047e^2/\hbar$ for fillings $ν=-1/2$ and $ν=-3/4$ , respectively, alongside specific transport signatures. Could these findings provide a pathway towards identifying and characterizing quantum criticality in emerging moiré superlattices?

Whispers of Chaos: Unveiling Moiré Superlattices

Moiré superlattices, created by twisting two layers of material, generate what are known as Moiré Chern Bands – unique electronic structures that dramatically alter how electrons behave. These bands offer an unprecedented level of control over electron interactions, allowing researchers to finely tune the strength of what’s known as ‘strong correlation’ – a situation where electrons influence each other significantly. This tunability makes these systems ideal for observing exotic quantum phenomena, most notably manifestations of the Quantum Hall Effect – where electron flow becomes quantized and incredibly precise, even in the absence of a traditional magnetic field. The ability to engineer these correlated states opens a pathway to explore fundamentally new states of matter and potentially harness their properties for advanced electronic devices, offering a versatile platform beyond traditional two-dimensional electron gases.

Moiré superlattices, when crafted from materials like twisted bilayer graphene, can host strikingly unusual electronic states, most notably the Composite Fermi Liquid (CFL). This phase emerges when electrons, subject to strong interactions and a powerful magnetic field, reorganize themselves into a new, collective state where each electron effectively carries a fraction of the fundamental charge. Unlike conventional Fermi Liquids where electrons behave as independent particles, the CFL exhibits drastically altered behavior – its properties are determined not by individual electrons, but by the correlated motion of these fractionally charged quasiparticles. This challenges established theoretical frameworks designed for simpler electronic systems, demanding new approaches to understand the complex interplay between electron-electron interactions and external fields, and opening doors to potential applications exploiting these novel quantum states of matter.

The transition between a Composite Fermi Liquid (CFL) and a Fermi Liquid (FL) state in moiré materials represents a critical frontier in condensed matter physics. This shift isn’t merely a change in material properties, but a fundamental alteration in how electrons collectively behave; the CFL, characterized by fractionalized excitations and long-range entanglement, gives way to the more conventional, independent-particle picture of the FL state. Precisely mapping this CFL-FL transition – identifying the controlling parameters like magnetic field and electron density, and understanding the role of disorder – is vital because it provides a testing ground for theories of strongly correlated electron systems. Researchers believe that unraveling the mechanisms governing this phase transition could reveal insights applicable to high-temperature superconductivity and other exotic quantum phenomena, potentially leading to the design of novel electronic devices and materials with unprecedented properties. The ability to tune and observe this transition in moiré systems offers an unparalleled opportunity to explore the delicate balance between quantum coherence and disorder that defines the behavior of electrons in these complex materials.

Fractionalizing the Electron: A Parton’s Perspective

The Parton Construction method addresses the complex physics occurring at the crossover between the CFL (co-linear metallic) and Fermi Liquid (FL) phases by mathematically representing electrons as composed of two distinct types of quasi-particles: charged and neutral sectors. This fractionalization is not a physical splitting of the electron, but rather a theoretical tool to simplify the analysis of strongly correlated electron systems. By separating the degrees of freedom associated with charge and neutrality, the many-body problem becomes more tractable, allowing for a focused examination of the interactions driving the phase transition. This approach effectively reduces the complexity of the full electron system by modeling it as two interacting sectors, each exhibiting simpler behavior than the original strongly correlated system.

The Parton Construction method employs Effective Field Theory (EFT) to systematically analyze the low-energy behavior arising from the fractionalization of electrons. This involves constructing an EFT Lagrangian containing fields representing the charged and neutral sectors, along with interaction terms describing their coupling. By focusing on the relevant degrees of freedom and symmetries at low energies, the EFT provides a controlled approximation to the full microscopic theory. This approach allows for the calculation of physical observables and the prediction of emergent phenomena, such as the collective behavior and excitations within these fractionalized sectors. The EFT framework facilitates the treatment of interactions beyond simple perturbative expansions, incorporating non-perturbative effects through appropriate operator ordering and regularization schemes.

The Emergent Gauge Field is a crucial component in describing the behavior of fractionalized electrons, specifically mediating interactions between the charged and neutral sectors resulting from the CFL-FL transition. This field isn’t a fundamental force but arises as a collective phenomenon from the strong interactions within the system. Its existence is mathematically formalized through a $U(1)$ gauge theory, and its topological implications are described by the Chern-Simons term in the effective action. The Chern-Simons term, proportional to $\in t a \wedge da$ , where $a$ is the emergent gauge field, introduces non-trivial topological effects and contributes to the system’s exotic properties, including the possibility of anyonic excitations.

Mapping the Transition: DC Conductivity as a Guide

DC conductivity quantifies a material’s ability to conduct direct current, representing the amount of current flowing per unit electric field. It is measured in Siemens per meter (S/m) and is a fundamental property characterizing a system’s electrical response. In the context of the CFL-FL transition, calculating DC conductivity $\sigma_{DC}$ provides a quantitative metric to assess the change in behavior as the system transitions between a coherent Fermi liquid (FL) and a non-Fermi liquid state exhibiting critical fluctuations. This calculation relies on understanding how charge carriers respond to an applied electric field, and is sensitive to the scattering processes that govern their motion within the material. By determining $\sigma_{DC}$ , researchers can precisely characterize the transport properties associated with the CFL-FL transition and compare theoretical predictions with experimental observations.

The Quantum Boltzmann Equation (QBE) is utilized to calculate DC conductivity by directly addressing the impact of inelastic scattering events on electron transport. Unlike simpler Drude models, the QBE considers the distribution function of electrons in momentum space and its evolution under the influence of both external fields and scattering processes. Inelastic scattering, arising from interactions with impurities, phonons, or other electrons, introduces energy dissipation and modifies the electron distribution, thus affecting the material’s electrical response. The QBE, when solved, yields the steady-state distribution function, which can then be used to determine the DC conductivity σ through the relation $\sigma = \frac{ne^2\tau}{m}$ , where $n$ is the carrier density, $e$ is the elementary charge, τ is the relaxation time determined by the scattering rate, and $m$ is the effective mass. Accurately modeling these scattering processes within the QBE framework is essential for obtaining quantitatively reliable predictions of DC conductivity.

The calculation of DC conductivity via the Quantum Boltzmann Equation is analytically challenging; therefore, the Large-N expansion is employed as a simplification technique. This method involves expanding the relevant equations in terms of 1/N, where N represents the number of flavors or internal states in the system. By retaining only the leading-order terms – those proportional to $1/N^0$ – the complexity of the calculation is significantly reduced, yielding a tractable result. This approach allows for the extraction of approximate, yet quantitatively meaningful, predictions for the DC conductivity, specifically enabling calculations of the universal conductivity values at fractional fillings like ν = -1/2 and ν = -3/4.

Calculations based on the Quantum Boltzmann Equation, simplified through the Large-N expansion, predict specific universal DC conductivities for certain fractional quantum Hall states. For the filling factor ν = -1/2, the calculated DC conductivity is approximately 0.033 $(e^2/ℏ)$ . At a filling factor of ν = -3/4, the predicted DC conductivity is approximately 0.047 $(e^2/ℏ)$ . These values represent leading-order corrections derived from the expansion and serve as quantifiable predictions for experimental verification of the theoretical model.

The derived DC conductivities of approximately 0.033 $(e^2/ℏ)$ at filling factor ν = -1/2 and 0.047 $(e^2/ℏ)$ at ν = -3/4 serve as benchmark results for validating the methodology employed. These predictions, obtained through a large-N expansion of the Quantum Boltzmann Equation, allow for direct comparison with experimental measurements of DC conductivity in similar systems. Discrepancies between theoretical predictions and experimental data can then be analyzed to refine the model or identify previously unaccounted-for physical effects. Furthermore, these specific instances demonstrate the applicability of the Quantum Boltzmann Equation and large-N expansion techniques to other correlated electron systems and provide a pathway for calculating transport properties in more complex scenarios.

Unveiling Microscopic Details: Probing System Response

The Propagator Equation, formally expressed as $G(x,t;x',t') = \langle T\{ \psi(x,t) \psi^\dagger(x',t') \} \rangle$ , mathematically describes the propagation of a quantum field, and thus the system’s response to an external perturbation. It directly connects microscopic interactions – represented by the field operators ψ and $\psi^\dagger$ – to measurable macroscopic properties. The equation accounts for all possible paths a particle can take between initial and final states, weighted by a phase factor determined by the action. By solving the Propagator Equation for a given system and external field, one can predict the system’s response, such as the induced current or polarization, thereby bridging the gap between fundamental interactions and observable phenomena. The time-ordering operator $T$ ensures causality in the calculation.

The Spectral Function, denoted as $A(\mathbf{k}, \omega)$ , provides the probability amplitude for adding or removing a particle with momentum $\mathbf{k}$ and energy ω. It directly relates to the Propagator Equation by serving as the key ingredient in its Lehmann representation. Specifically, the Propagator can be expressed as an integral over the Spectral Function, effectively decomposing the system’s response into contributions from individual excitations. Accurate interpretation of the Propagator therefore necessitates a precise understanding of the Spectral Function’s shape and features, including peak positions, widths, and overall energy distribution, as these directly reflect the available states and their lifetimes within the system.

Damping mechanisms are critical for accurately modeling system behavior because they account for the finite lifetime of excited states. Landau damping, a specific collisionless damping process, arises from the interaction of waves with resonant particles, leading to a transfer of energy from the wave to the particles and a subsequent reduction in wave amplitude. This process is velocity-dependent; particles moving near the wave’s phase velocity contribute most significantly to the damping. The damping rate, proportional to the inverse of the excitation lifetime Γ, directly impacts the width of spectral features and modifies the system’s response as predicted by the Propagator Equation, necessitating its inclusion for quantitative accuracy and realistic simulations.

A comprehensive understanding of system response is achieved by integrating the Propagator Equation, the Spectral Function, and considerations of damping mechanisms like Landau Damping. The Propagator Equation mathematically describes how the system evolves under external influence, while the Spectral Function details the energy distribution of excitations within it. Inclusion of damping effects accounts for the finite lifetime of these excitations, preventing unphysical results. This combined approach provides a complete theoretical description against which experimental data can be rigorously compared, allowing for validation or refinement of the underlying theoretical framework and ensuring the model accurately reflects observed system behavior.

Implications for Correlated Electron Systems: A Wider Perspective

The behavior of strongly correlated electron systems, where electron-electron interactions dominate, often defies conventional descriptions of phase transitions. Recent theoretical work leverages the concept of “partons” – hypothetical particles representing fragments of electrons – to construct a powerful framework for understanding these unconventional transitions. This approach effectively decomposes the complex many-body problem into interactions between these partons, allowing researchers to map the system’s behavior onto simpler, more tractable models. Through detailed calculations based on this parton construction, physicists can now predict and interpret phase diagrams exhibiting behaviors like fractionalization and topological order – phenomena not readily explained by traditional methods. The strength of this framework lies in its ability to capture the collective behavior arising from strong correlations, providing valuable insights into the emergence of exotic states of matter and offering a new lens through which to investigate materials with complex electronic properties.

The principles uncovered through the study of moiré systems, where strong electron correlations give rise to exotic phenomena, extend far beyond these specifically engineered structures. Researchers find that the underlying physics – the fractionalization of electrons into emergent “partons” and the resulting unconventional phase transitions – are likely present in a diverse array of materials. These include high-temperature superconductors, heavy fermion compounds, and certain transition metal oxides, all exhibiting strong electron-electron interactions and complex electronic behaviors. This broad applicability stems from the fundamental nature of the parton construction, which provides a robust framework for describing systems where traditional, single-particle approaches fail. Consequently, the insights gained from moiré materials are not merely a curiosity limited to artificial lattices, but a potentially unifying principle for understanding and ultimately controlling correlated electron behavior across a wide spectrum of condensed matter physics.

Continued development of these analytical techniques holds the potential to unlock a more complete understanding of exotic states of matter, such as unconventional superconductivity and topological phases. By refining the parton construction and associated calculations, researchers aim to move beyond simplified models and address the complexities inherent in strongly correlated electron systems. This includes accurately capturing the interplay between different electronic orders and the emergence of collective phenomena. Such advancements aren’t merely academic; a deeper comprehension of these materials’ fundamental properties paves the way for the discovery and design of novel electronic devices with unprecedented functionalities, potentially revolutionizing fields like energy storage, quantum computing, and advanced materials science. Ultimately, these methods promise to reveal how collective electronic behavior gives rise to macroscopic properties, bridging the gap between microscopic interactions and observable phenomena.

The developed methodology transcends immediate applications, offering a systematic pathway to investigate increasingly intricate electronic states and material behaviors. By establishing a robust framework for dissecting correlated electron systems, researchers gain the ability to predict and control the emergence of novel functionalities. This predictive power extends beyond simply observing exotic phases; it enables the rational design of materials tailored for specific purposes, such as high-temperature superconductivity or advanced quantum computing. The approach facilitates exploration of scenarios involving multiple interacting electronic orders and complex band structures, ultimately paving the way for a new era of materials discovery and technological innovation based on a deeper understanding of quantum matter.

The pursuit of universal signatures in these Moiré systems feels less like physics and more like attempting to divine order from static. This work, meticulously charting the transition from composite Fermi liquid to conventional metal, assumes a rationality within the chaos that feels… optimistic. It’s a hunt for predictable d.c. conductivities, a desire to normalize the unnormalized. As Søren Kierkegaard observed, “Life can only be understood backwards; but it must be lived forwards.” Perhaps this is the essence of it – to build models that appear to explain the forward march, knowing full well they’re reconstructions of a past that never quite existed. The data whispers, and this paper attempts to translate, even if the translation is, inevitably, a carefully constructed fiction.

What’s Next?

The prediction of quantifiable conductivities at this purported quantum critical point is, naturally, an invitation for experimentalists to find ways to disagree. The elegance of the theoretical framework-Chern-Simons theory, the quantum Boltzmann equation-offers little solace when faced with the inherent messiness of actual materials. It’s not that the physics is wrong; it’s that the materials will insist on being inconveniently complex, offering a spectrum of behaviors that mock the desire for a clean transition. The pursuit of universality often ends in a catalog of exceptions.

The real challenge, it seems, isn’t to find the predicted signatures, but to convincingly explain their absence. Or, perhaps more fruitfully, to develop a more nuanced understanding of how these moiré systems actively resist simple categorization. The composite Fermi liquid, after all, is a construct-a useful fiction. The materials themselves are under no obligation to conform to its tidy logic. Expect a proliferation of effective models, each attempting to patch the holes in the last, like desperate theologians revising dogma.

Ultimately, the field will likely shift its focus, not toward finer measurements of conductivity, but toward a deeper interrogation of the assumptions embedded within the theoretical tools themselves. Regression is a prayer, and p-values are merely superstitious gestures in the face of irreducible uncertainty. The true prize isn’t a confirmed prediction, but a better story about why the materials consistently refuse to be predictable.

Original article: https://arxiv.org/pdf/2602.15334.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/