Taming Radiation: Simulating Charged Particle Dynamics in Magnetic Fields

Author: Denis Avetisyan

Researchers have developed a novel simulation framework to model the complex interplay between charged particles, magnetic fields, and the radiation they emit.

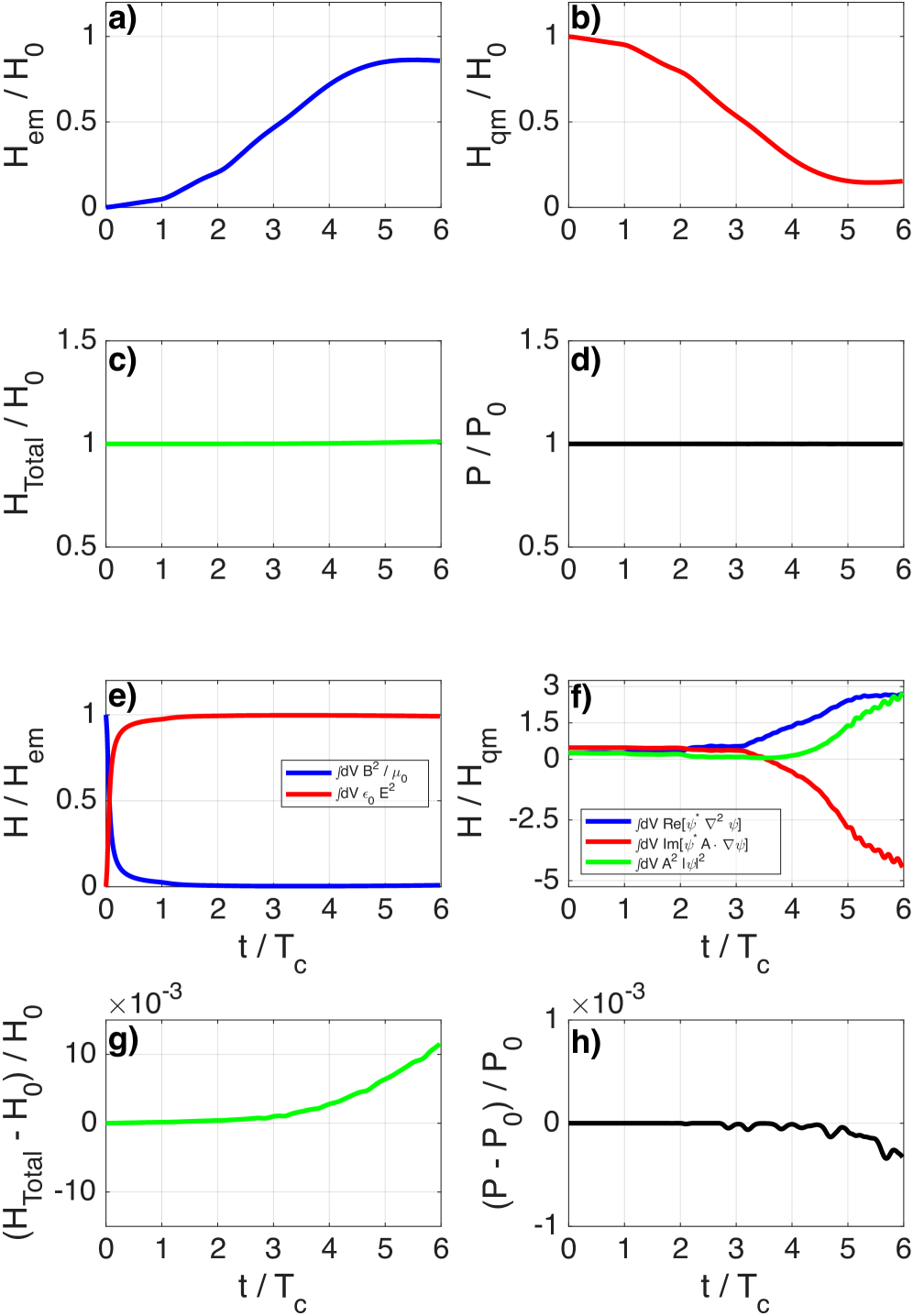
The simulation demonstrates the conservation of total energy and probability density over six cyclotron periods, revealing how the system’s energy partitions between quantum <span class="katex-eq" data-katex-display="false">H_{qm}</span> and electromagnetic <span class="katex-eq" data-katex-display="false">H_{em}</span> subsystems-with plots detailing their evolution relative to initial values <span class="katex-eq" data-katex-display="false">H_0</span> and <span class="katex-eq" data-katex-display="false">P_0</span>-and quantifying minimal error in both total energy and probability density conservation throughout the modeled interaction. — The simulation demonstrates the conservation of total energy and probability density over six cyclotron periods, revealing how the system’s energy partitions between quantum $H_{qm}$ and electromagnetic $H_{em}$ subsystems-with plots detailing their evolution relative to initial values $H_0$ and $P_0$ -and quantifying minimal error in both total energy and probability density conservation throughout the modeled interaction.

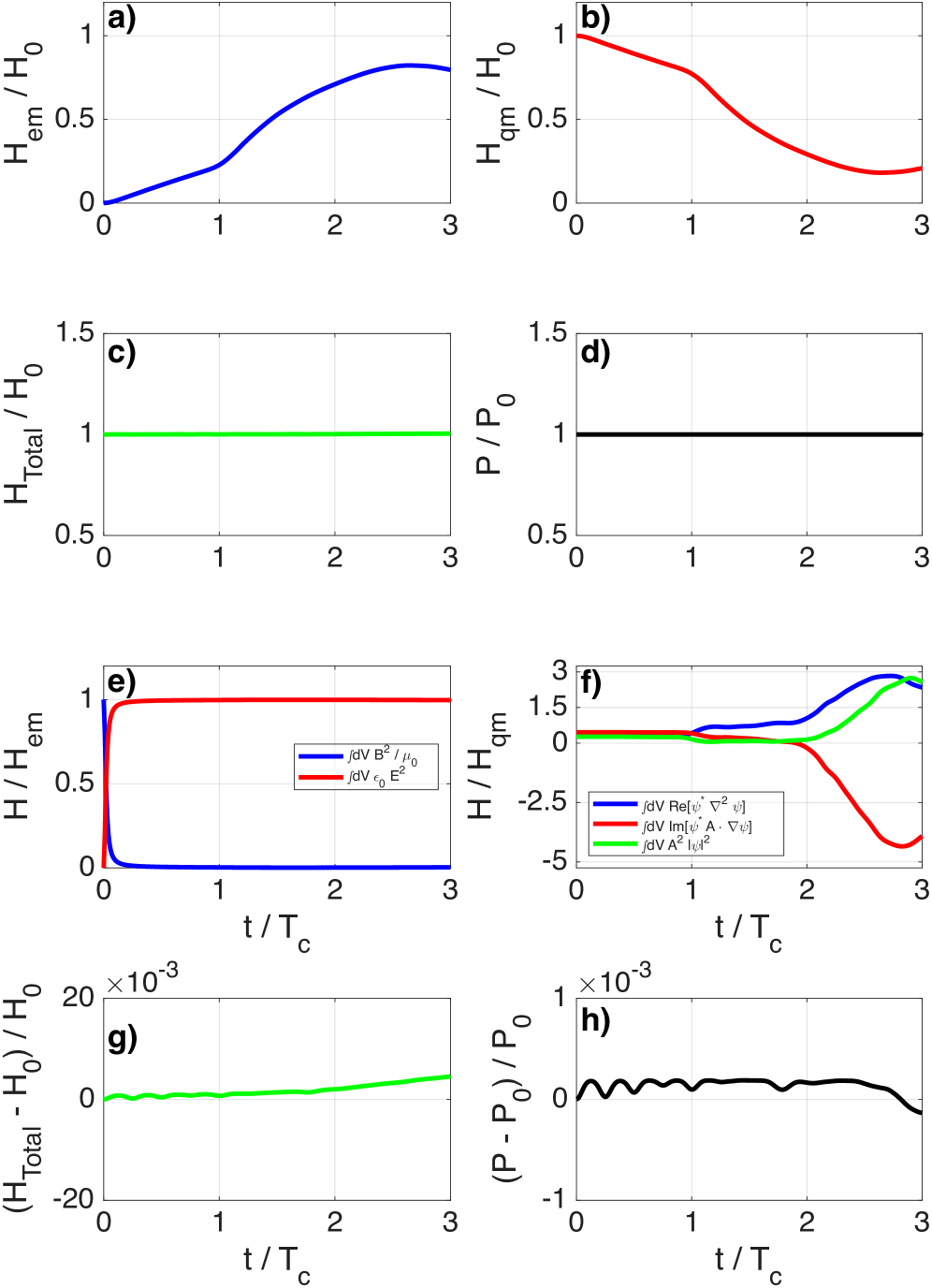
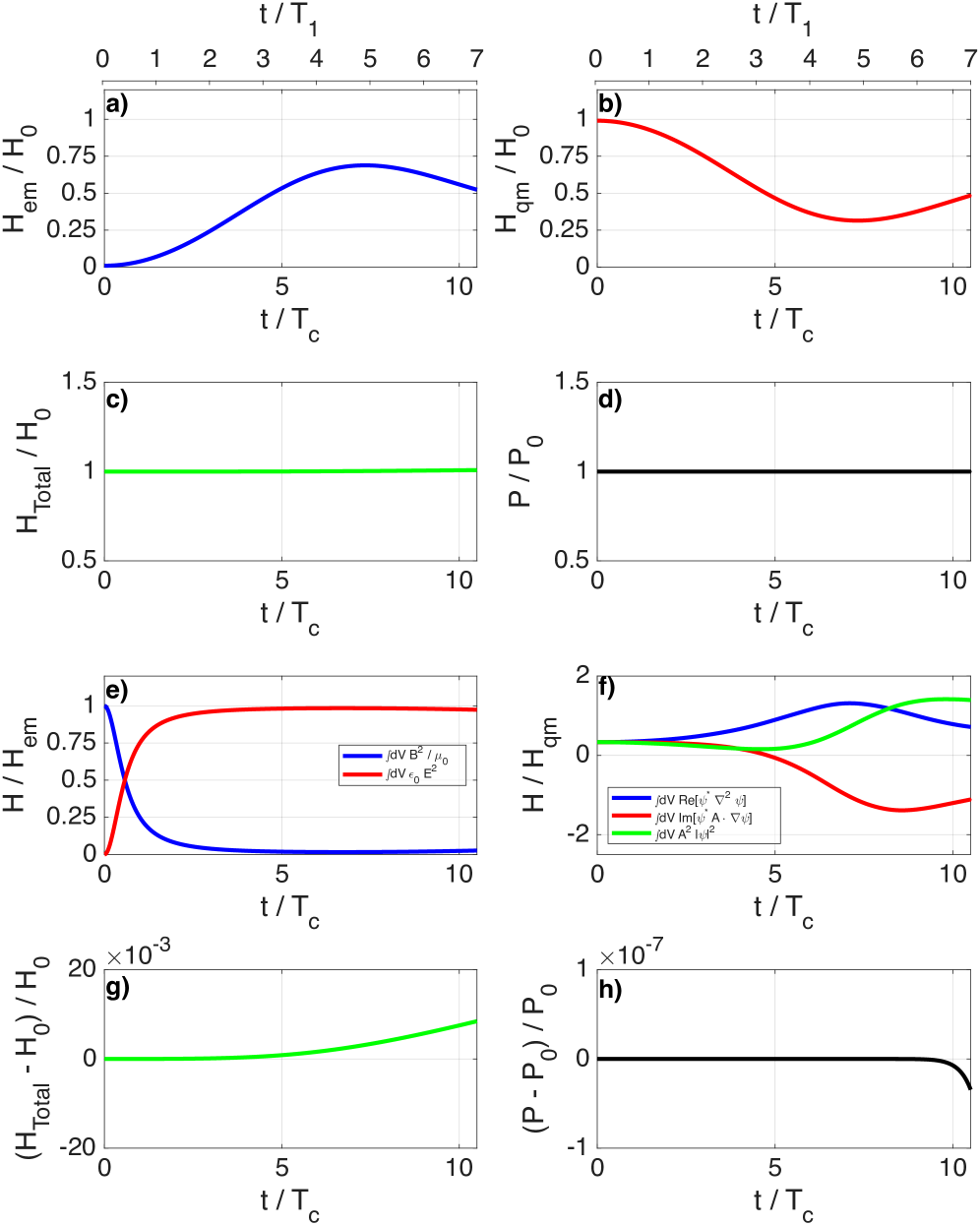
This work presents a self-consistent solution to the coupled Schrödinger-Maxwell system, enabling detailed analysis of Landau level dynamics and radiation reaction effects on particle motion.

The conventional treatment of charged particle radiation reaction breaks down at atomic scales, undermining the very concept of a radiation reaction force. This limitation motivates the work presented in ‘Self-Consistent Dynamics of Electron Radiation Reaction via Structure-Preserving Geometric Algorithms for Coupled Schrödinger-Maxwell Systems’, which introduces a novel numerical framework-implemented in the SPHINX code-to simulate the fully-coupled, nonlinear dynamics of an electron in a magnetic field. These simulations reveal that coherent electron states rapidly lose coherence due to radiation reaction, while Landau levels renormalize into stationary dressed eigenstates with conserved energy, demonstrating a self-consistent interplay between the particle and the electromagnetic field. Will this approach unlock a more accurate understanding of extreme-field phenomena in areas like fusion plasmas and next-generation laser experiments?

The Interplay of Fields: A Foundation for Holistic Simulation

The behavior of charged particles, fundamental to diverse phenomena from plasma physics to materials science, necessitates the concurrent solution of the Schrödinger equation – governing quantum mechanical evolution – and Maxwell’s equations, which describe electromagnetic fields. This simultaneous requirement arises because the particle’s quantum state directly influences the electromagnetic field it generates, and conversely, the field shapes the particle’s motion and quantum properties. However, this coupled system presents formidable computational challenges; the complexity scales rapidly with the number of particles and the precision required to resolve both quantum and electromagnetic effects. Traditional computational methods often struggle with this interplay, demanding excessive resources or sacrificing accuracy when attempting to model these intrinsically linked systems. Successfully simulating these interactions is crucial for predicting the behavior of complex physical systems, and necessitates advanced algorithms capable of handling the inherent complexities of coupled quantum-electromagnetic dynamics.

Historically, modeling interactions between physical fields has frequently relied on decoupling the governing equations – for example, treating the Schrödinger equation, which describes quantum particles, and Maxwell’s equations, which govern electromagnetism, as independent entities. However, when these systems exhibit strong coupling – meaning a significant exchange of energy and information – this separation introduces substantial inaccuracies. The independent treatment fails to capture the feedback loops inherent in the coupled system, leading to unphysical results and numerical instability in simulations. This is because changes in one field directly influence the other, and a separate solution fails to account for this dynamic interplay. Consequently, advanced simulation techniques are necessary to solve these equations simultaneously, preserving the correlation between the fields and ensuring reliable predictive power.

Reliable simulation of tightly linked physical systems, such as those involving charged particles and electromagnetic fields, hinges on maintaining the geometric structure inherent to the problem. Traditional methods often decouple the governing equations – Schrödinger’s equation for particle behavior and Maxwell’s equations for fields – which can introduce errors and instability when strong interactions occur. A robust framework instead necessitates a unified approach that respects these geometric properties, ensuring conservation laws are accurately upheld throughout the simulation. Critically, the timescale for these simulations is often dictated by the cyclotron period, $2π/ωc$ , which represents the time it takes for a charged particle to orbit in a magnetic field; accurately resolving phenomena at this timescale is essential for capturing the system’s dynamic behavior and generating dependable predictions.

Over three cyclotron periods, the simulation demonstrates the conservation of total energy <span class="katex-eq" data-katex-display="false">H_{Total}</span>, electromagnetic energy <span class="katex-eq" data-katex-display="false">H_{em}</span>, and quantum energy <span class="katex-eq" data-katex-display="false">H_{qm}</span>, as well as the conservation of probability <span class="katex-eq" data-katex-display="false">P</span>, with minimal error in both total energy and probability over time. — Over three cyclotron periods, the simulation demonstrates the conservation of total energy $H_{Total}$ , electromagnetic energy $H_{em}$ , and quantum energy $H_{qm}$ , as well as the conservation of probability $P$ , with minimal error in both total energy and probability over time.

Preserving Structure: A Geometric Path to Accuracy

The Symplectic Splitting Scheme is a numerical method used to approximate solutions to the coupled Schrödinger-Maxwell equations, a system frequently encountered in quantum optics and plasma physics. Its core strength lies in its ability to preserve geometric invariants – quantities that remain constant throughout the simulation despite numerical approximations. This is achieved by alternating between solving the Schrödinger equation and the Maxwell equations in separate steps. By decoupling the system in this manner, the scheme avoids introducing spurious numerical artifacts that can lead to instability or inaccurate results, particularly in long-time simulations. Preserving these invariants is critical for ensuring the physical validity and long-term accuracy of the numerical solution, as it reflects the underlying conservation laws governing the system’s behavior.

The symplectic splitting scheme achieves accuracy in simulating the coupled Schrödinger-Maxwell system by sequentially solving each equation. This alternating approach, known as operator splitting, leverages the Hamiltonian structure inherent in the combined system. By solving the Schrödinger equation, then the Maxwell equations, and repeating this process, the scheme preserves the symplectic structure – a geometric property related to volume preservation in phase space – which is crucial for long-term stability and accurate representation of the system’s dynamics. This preservation arises because each substep – solving either Schrödinger or Maxwell – is itself a symplectic integrator, and the composition of symplectic integrators remains symplectic under certain conditions.

The SPHINX Solver is a MATLAB-based computational platform designed for simulating the coupled Schrödinger-Maxwell system using the Symplectic Splitting Scheme. Its implementation prioritizes both robustness and computational efficiency. Simulations conducted with SPHINX utilize a time step size dependent on the parameter β, with a value of 2.51 x 10^-4 employed for β=10 and 8.376 x 10^-5 for β=5. These specific time step values were determined to balance simulation accuracy and computational cost within the framework of the symplectic scheme.

Particle Dynamics: From Cyclotron Motion to Radiation Emission

Charged particle motion within a magnetic field is fundamentally characterized by cyclotron motion, a circular trajectory resulting from the Lorentz force. This force, described by the equation $\mathbf{F} = q(\mathbf{v} \times \mathbf{B})$ , where q is the charge, $\mathbf{v}$ is the velocity, and $\mathbf{B}$ is the magnetic field, acts perpendicularly to both the particle’s velocity and the magnetic field direction, causing the particle to move in a helical path. The angular frequency of this motion, known as the cyclotron frequency $\omega_c$ , is given by $\omega_c = \frac{qB}{m}$ , where m is the mass of the particle. A complete quantum mechanical description of this motion is obtained through the Schrödinger Equation, accounting for the particle’s wave-like nature and the potential energy associated with the magnetic field.

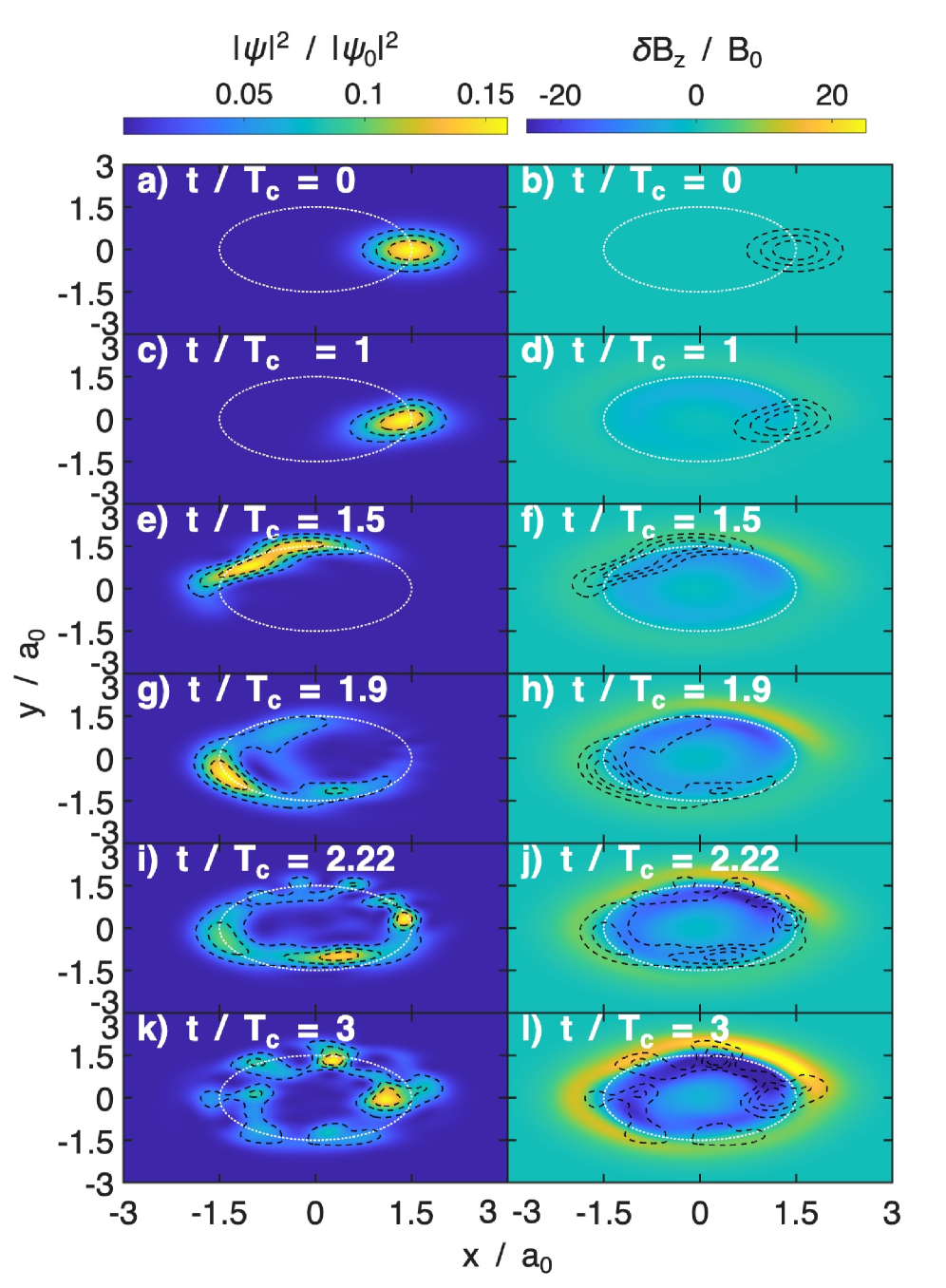
The emission of electromagnetic radiation by accelerating charged particles is described by the Radiation Reaction. This reaction manifests as a damping force proportional to the square of the particle’s acceleration, effectively reducing its kinetic energy and altering its trajectory from the purely circular cyclotron motion. The force is a consequence of the particle itself interacting with the electromagnetic field it generates; as the particle accelerates, it emits photons, carrying away energy and momentum. This energy loss results in a continuous deceleration, and the resulting radiation spectrum is dependent on the particle’s acceleration profile. The Radiation Reaction is often incorporated into the particle’s equation of motion as an additional force term, modifying its canonical momentum and leading to deviations from classical cyclotron behavior.

The combined effect of cyclotron motion and radiation reaction introduces deviations from ideal circular particle trajectories. Simulations demonstrate that as particle velocity approaches relativistic speeds – specifically with β = v/c = 10 – the resulting electromagnetic radiation generates a substantial perturbation in the background magnetic field. Observed values of $\frac{\delta B_z}{B_0}$ reach approximately 80, indicating a significant transfer of energy from the particle to the radiated field and a considerable alteration of the particle’s momentum. This phenomenon is crucial for understanding the production of synchrotron radiation, where highly energetic charged particles emit intense electromagnetic radiation as they spiral within magnetic fields.

A fully coupled simulation with <span class="katex-eq" data-katex-display="false">\beta=5</span> demonstrates the dynamic evolution of the probability density <span class="katex-eq" data-katex-display="false">|Ψ|^2</span> and the perturbed magnetic field <span class="katex-eq" data-katex-display="false">\delta B_z</span> over three cyclotron periods, with contours of <span class="katex-eq" data-katex-display="false">|Ψ|^2</span> and the Larmor radius <span class="katex-eq" data-katex-display="false">\rho_{\ell}</span> providing spatial context. — A fully coupled simulation with $\beta=5$ demonstrates the dynamic evolution of the probability density $|Ψ|^2$ and the perturbed magnetic field $\delta B_z$ over three cyclotron periods, with contours of $|Ψ|^2$ and the Larmor radius $\rho_{\ell}$ providing spatial context.

The Mathematical Foundation: Describing the Electromagnetic Landscape

The Electromagnetic Tensor, formally represented as $F_{\mu\nu}$ , is a second-rank antisymmetric tensor used to encapsulate both the electric field $\mathbf{E}$ and the magnetic field $\mathbf{B}$ into a single mathematical object. Its components are defined such that $F^{\mu\nu} = \partial^{\mu}A^{\nu} - \partial^{\nu}A^{\mu}$ , where $A^{\mu}$ is the four-potential. This compact representation significantly simplifies the formulation of Maxwell’s Equations, allowing them to be expressed in a manifestly Lorentz covariant form. Specifically, the four equations are consolidated into a single equation: $\partial_{\mu}F^{\mu\nu} = \mu_0 J^{\nu}$ , where $J^{\nu}$ is the four-current. The tensor simplifies calculations involving electromagnetic interactions and facilitates the application of special relativity to electromagnetic phenomena.

The gauge covariant derivative is a mathematical construct used in electromagnetism to ensure that physical laws remain consistent regardless of the choice of electromagnetic potential. Specifically, it modifies the standard derivative operator when calculating the effect of electromagnetic fields on charged particles; instead of a simple gradient, it incorporates the vector potential $\mathbf{A}$ and, for time-varying fields, the scalar potential φ. This modification is crucial because the electromagnetic potentials are not uniquely defined; a gauge transformation-changing $\mathbf{A}$ and φ without altering the electric and magnetic fields themselves-can be performed without affecting physical observables. The gauge covariant derivative, defined as $\nabla - iq\mathbf{A}$ (where $q$ is the charge), transforms in a way that leaves the calculated physical quantities invariant under these gauge transformations, thereby preserving the consistency of the theoretical framework.

Accurate modeling of electromagnetic field interactions with quantum particles relies on a robust mathematical framework. Simulations demonstrate a correlation between the paramagnetic energy becoming negative – observed around $t/T_c \approx 2.06$ for $\beta = 5$ – and the phenomenon of wave packet fractionation. This negative energy regime indicates instability and the potential for particle dissociation, directly linked to the spreading and separation of the wave packet describing the particle’s quantum state. These simulation results highlight the importance of precisely capturing electromagnetic interactions to predict and understand quantum particle behavior under varying field conditions.

Over two periods of the <span class="katex-eq" data-katex-display="false">\omega_1</span> eigenmode, the system conserves total energy, electromagnetic energy, and quantum energy, as demonstrated by the stable evolution of <span class="katex-eq" data-katex-display="false">H_{Total}</span>, <span class="katex-eq" data-katex-display="false">H_{em}</span>, and <span class="katex-eq" data-katex-display="false">H_{qm}</span> relative to their initial values, and maintains a constant probability density <span class="katex-eq" data-katex-display="false">P</span> over time, with minimal error in both total energy and probability density. — Over two periods of the $\omega_1$ eigenmode, the system conserves total energy, electromagnetic energy, and quantum energy, as demonstrated by the stable evolution of $H_{Total}$ , $H_{em}$ , and $H_{qm}$ relative to their initial values, and maintains a constant probability density $P$ over time, with minimal error in both total energy and probability density.

Quantum States and Coherence: Bridging the Quantum and Classical Realms

Quantum mechanics often describes reality in terms of probabilities, but coherent states offer a fascinating bridge to classical intuition. These special quantum states minimize the uncertainty inherent in simultaneously knowing a particle’s position and momentum, a principle dictated by Heisenberg’s uncertainty principle. In the context of a magnetic field, a particle-like an electron-doesn’t occupy a single, definite location, but rather exists as a superposition of possibilities, described by a wave function. Coherent states allow this wave function to resemble a classical particle orbiting within the field, exhibiting behavior analogous to that predicted by classical electromagnetism. This doesn’t mean the particle is classical, but rather that certain properties-like its average position and momentum-can be described with a degree of certainty approaching that of a classical object, simplifying the analysis of its behavior and providing valuable insights into the quantum-classical transition. The energy associated with these states is not continuous, but instead quantized into discrete levels known as Landau Levels $\hbar \omega_c (n + \frac{1}{2})$ , where $\omega_c$ is the cyclotron frequency and n is a non-negative integer, further demonstrating the unique interplay between quantum and classical descriptions.

Quantum coherent states aren’t simply plucked from the void; they are meticulously built upon the fundamental quantum vacuum state. This construction utilizes a mathematical tool known as the Displacement Operator, which effectively shifts, or ‘displaces’, the particle’s initial position in phase space. Imagine the vacuum state as the ground level; the Displacement Operator acts as an elevator, raising the particle to a specific, defined location without altering its intrinsic quantum properties. This process doesn’t introduce additional quanta of energy; instead, it re-positions the existing quantum fluctuations, creating a state that closely resembles a classical particle with a definite position and momentum – albeit still governed by the inherent uncertainties of quantum mechanics. The resulting coherent state, described mathematically as $|\alpha\rangle = D(\alpha)|0\rangle$ , exhibits minimal uncertainty and serves as a cornerstone for understanding the behavior of quantum systems in external fields.

When a charged particle exists within a magnetic field, its motion becomes fundamentally altered, leading to the quantization of its energy into discrete levels known as Landau Levels. These levels aren’t merely a theoretical curiosity; they dramatically influence the particle’s behavior, restricting its motion perpendicular to the field and resulting in a cyclical trajectory. The energy separation between these levels is directly proportional to the strength of the magnetic field – a stronger field leads to more widely spaced levels, described by the equation $\hbar\omega_c = eB$ , where $\hbar$ is the reduced Planck constant, $e$ is the elementary charge, and $B$ is the magnetic field strength. Consequently, Landau Levels dictate the spectral properties of the particle, manifesting as distinct peaks in measurements of absorbed or emitted radiation and forming the basis for phenomena like the Quantum Hall Effect, where electrical conductivity becomes precisely quantized due to the influence of these energy levels.

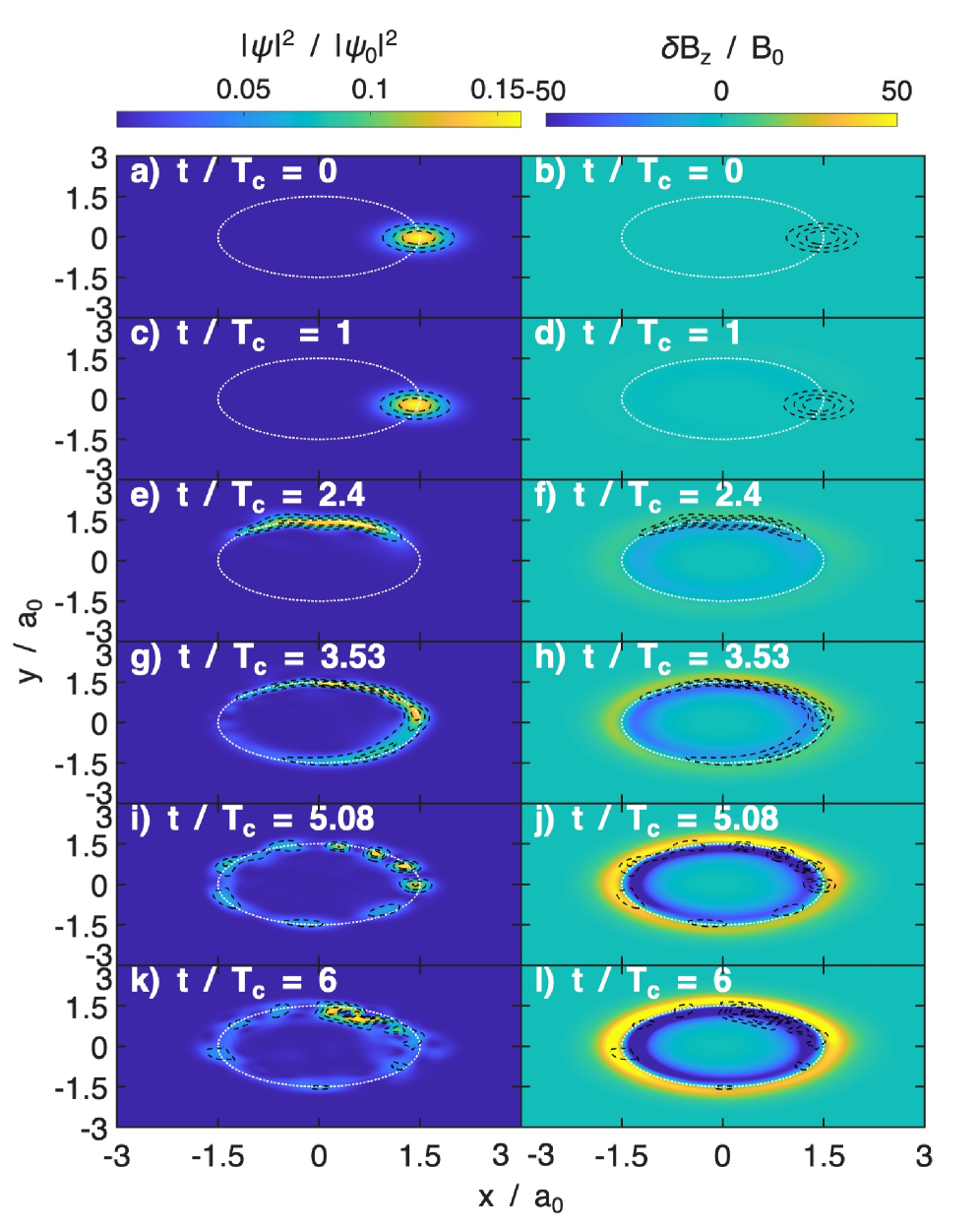
A fully coupled simulation with <span class="katex-eq" data-katex-display="false">\beta=10</span> reveals the dynamic interplay between the probability density <span class="katex-eq" data-katex-display="false">|Ψ|^2</span> and the perturbed magnetic field <span class="katex-eq" data-katex-display="false">\delta B_z</span> over six cyclotron periods, with contours of <span class="katex-eq" data-katex-display="false">|Ψ|^2</span> and the Larmor radius <span class="katex-eq" data-katex-display="false">\rho_{\ell}</span> providing spatial context. — A fully coupled simulation with $\beta=10$ reveals the dynamic interplay between the probability density $|Ψ|^2$ and the perturbed magnetic field $\delta B_z$ over six cyclotron periods, with contours of $|Ψ|^2$ and the Larmor radius $\rho_{\ell}$ providing spatial context.

The presented work illuminates a fundamental principle: structure dictates behavior. Much like an architect designs for emergent properties, this simulation demonstrates how the interplay between the Schrödinger-Maxwell system and the particle’s interaction with its own radiation field yields complex dynamics. The self-consistent approach isn’t merely a computational technique; it’s an acknowledgement that optimizing one element-here, accounting for radiation reaction-inevitably introduces tension elsewhere, impacting the stability of Landau levels and the overall system behavior. As Wilhelm Röntgen observed, “I have made the discovery that these rays act photographically on sensitized plates, and that they can pass through many substances.” This mirrors the simulation’s capacity to ‘see through’ the complexities of coupled equations, revealing the previously hidden interplay between particle motion and electromagnetic fields.

Beyond the Spiral: Charting Future Courses

The presented work, while demonstrating a self-consistent treatment of radiation reaction within the Schrödinger-Maxwell framework, subtly highlights the inherent difficulty in isolating a ‘particle’ from its field. The simulation’s fidelity rests on geometric integrators, acknowledging that the true physics resides not in the equations themselves, but in the preservation of underlying structure during time evolution. Documentation captures structure, but behavior emerges through interaction. Consequently, future investigation should not focus solely on refining the numerics, but on extending the framework to encompass multiple interacting particles, where collective effects will inevitably dominate.

A critical limitation remains the reliance on coherent states. While mathematically convenient, these states represent a particular, and arguably artificial, simplification of the quantum reality. Exploring the impact of initial state choice – venturing beyond the Gaussian approximations – will be crucial. One anticipates that the introduction of even modest wavefunction complexity will reveal previously hidden instabilities and resonances, demanding a more nuanced understanding of the interplay between quantum mechanics and classical radiation.

Ultimately, the pursuit of a truly self-consistent theory requires a shift in perspective. The problem is not simply to solve the Schrödinger-Maxwell equations, but to understand how the emergence of classical behavior from quantum foundations necessitates a rethinking of the very notion of a ‘particle’ and its interaction with the electromagnetic field. The long-term challenge lies not in achieving greater numerical precision, but in crafting a conceptual framework that embraces the inherent interconnectedness of the system as a whole.

Original article: https://arxiv.org/pdf/2602.17429.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/