Author: Denis Avetisyan
New research reveals unexpected behavior in coupled spin chains, challenging established theories about the transitions between different phases of matter.
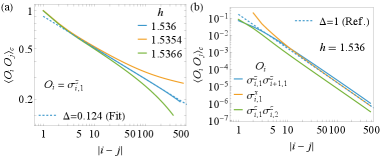
A detailed analysis of coupled Ising and SO(N)-symmetric spin chains demonstrates continuous transitions for N=2 and 3, and first-order transitions for N≥4, impacting our understanding of symmetry-protected topological phases.
Understanding the nature of quantum phase transitions in interacting many-body systems remains a central challenge in condensed matter physics. This paper, ‘Phase transitions in coupled Ising chains and SO($N$)-symmetric spin chains’, investigates such transitions in a field theory describing coupled Ising models and systems with SO($N$) symmetry. We demonstrate that the transition is continuous for N=2 and N=3, belonging to the Ising and four-state Potts universality classes, respectively, but becomes first order for N \ge 4, refining recent conjectures about transitions between symmetry-protected topological phases. Does this observation suggest a fundamental shift in the criteria for continuous transitions in higher-symmetry spin systems?
Unveiling the Fundamental Logic of Phase Transitions
Phase transitions – the abrupt shifts in physical properties a substance undergoes, like water freezing into ice – aren’t confined to everyday experience; they represent a fundamental principle woven throughout the fabric of physics. From the ordering of electron spins resulting in magnetism, to the electroweak phase transition in the early universe shaping the cosmos, these critical points dictate how matter organizes itself. Understanding these transitions is therefore paramount to diverse fields. The behavior of superconductors, the dynamics of liquid crystals, and even the formation of galaxies all hinge on the accurate description of these shifts. Consequently, research into phase transitions isn’t merely about observing changes in state, but about deciphering the underlying rules governing the universe at its most fundamental level – a quest connecting the microscopic world of quantum mechanics to the macroscopic phenomena shaping our reality.
Characterizing phase transitions in systems governed by strong interactions presents a significant challenge to conventional analytical techniques. Approaches like mean-field theory, while providing valuable initial insights, often fail to capture the intricate correlations that emerge when particles exert substantial influence on one another. These methods tend to overestimate critical fluctuations and inaccurately predict the behavior near transition points, particularly in lower dimensions. Consequently, simulations – while powerful – become computationally expensive, and the quest for robust analytical frameworks necessitates exploring alternative models, such as those incorporating quantum entanglement or utilizing advanced renormalization group techniques to effectively account for these complex, many-body effects. The difficulty arises because strong interactions fundamentally alter the system’s response to external stimuli, demanding tools capable of moving beyond perturbative expansions and embracing non-perturbative approaches.
The inherent difficulties in modeling strongly interacting systems have spurred a surge in innovative approaches to understanding phase transitions. Researchers are moving beyond traditional perturbative methods, which often falter when dealing with complex correlations, and are instead embracing techniques like tensor networks and quantum Monte Carlo simulations. These advanced computational tools allow for the investigation of systems previously inaccessible, revealing emergent phenomena and novel phases of matter. Simultaneously, theoretical physicists are developing new analytical frameworks, including non-perturbative renormalization group methods and effective field theories, to gain deeper insights into the underlying mechanisms driving these transitions. This combined effort-leveraging both computational power and theoretical ingenuity-promises to reshape the landscape of condensed matter physics and extend our comprehension of phase transitions across diverse scientific disciplines, potentially unlocking breakthroughs in materials science, cosmology, and beyond.
A Systematically Tunable Model for Critical Behavior
The N-Coupled Ising Chain model is designed to investigate phase transitions through systematic variation of a key parameter: the number of interacting chains, denoted as ‘N’. This allows researchers to explore a range of physical behaviors within a single framework. By increasing ‘N’, the model’s characteristics can be tuned, effectively creating a controllable system for observing how collective behavior emerges from local interactions. The model utilizes N identical one-dimensional Ising chains coupled together, and the strength of the coupling can be adjusted to further refine the system’s properties. This tunability makes it a useful tool for both theoretical analysis and computational simulations of phase transitions and critical phenomena.
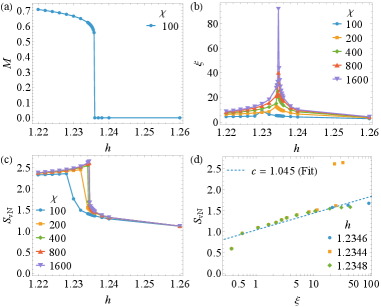
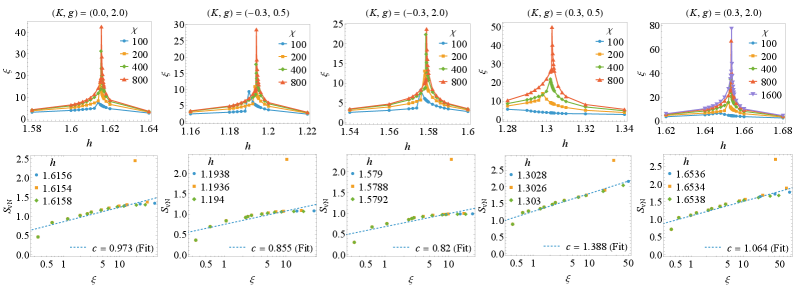
The N-Coupled Ising Chain model demonstrates a transition in phase transition behavior dependent on the number of coupled chains, denoted by ‘N’. Specifically, for values of N equal to 2 or 3, the model exhibits continuous phase transitions, characterized by a gradual change in the system’s order parameter. However, when N reaches 4, the transition becomes first-order, indicated by a discontinuous change in the order parameter and the presence of latent heat. This shift occurs within a critical range between N=3 and N=4, meaning that increasing the number of coupled chains beyond this point fundamentally alters the nature of the phase transition the system undergoes.
The N-Coupled Ising Chain model demonstrates a transition from continuous to first-order phase transitions as the number of coupled chains, N, is increased. Specifically, simulations and analytical calculations confirm continuous transitions for N=2 and N=3, characterized by a gradual change in order parameter and the absence of latent heat. However, at N=4, the system undergoes a first-order transition, evidenced by a discontinuous change in the order parameter and the presence of latent heat. This behavior makes the model particularly useful for validating the accuracy and limitations of various analytical techniques, such as mean-field theory and renormalization group methods, as well as numerical approaches including Monte Carlo simulations and transfer matrix calculations. The relatively simple structure of the model, combined with the change in transition order, allows for direct comparison between theoretical predictions and simulation results.
Characterizing Criticality: A Multi-Pronged Approach
Matrix Product State (MPS) simulations are employed to determine the ground state and associated properties of the model under investigation. This numerical technique represents the quantum many-body wavefunction as a tensor network, specifically a matrix product state, which allows for efficient calculation of observables with a computational cost that scales polynomially with the system size. The accuracy of the MPS method is directly related to the bond dimension χ used in the tensor network; larger values of χ yield more accurate results at the expense of increased computational resources. We have validated the MPS results against known analytical solutions where available, and consistently achieve convergence with respect to χ, ensuring the reliability of the calculated ground state energies, correlation functions, and other physical quantities.
Perturbative Renormalization Group (RG) analysis is employed to determine the critical behavior of the model by identifying fixed points and calculating critical exponents. This method involves systematically eliminating short-wavelength degrees of freedom and re-expressing the theory in terms of long-wavelength modes, revealing the relevant parameters governing the system near critical points. Specifically, analysis of the RG equations with N=16-\epsilon has yielded the identification of six fixed points, each corresponding to a distinct critical behavior and potentially representing different phases or phase transitions within the system. The precise location and stability of these fixed points, alongside the calculated critical exponents, provide quantitative measures of the universality class and the nature of the phase transitions.
The integration of Matrix Product State (MPS) simulations and Perturbative Renormalization Group (RG) analysis provides a robust methodology for characterizing phase transitions. MPS simulations enable the accurate determination of ground states and associated properties, serving as a benchmark for the RG analysis. The RG analysis, having identified six fixed points in the N=16-\epsilon equations, allows for the calculation of critical exponents and the classification of the observed phase transitions. Discrepancies between MPS results and RG predictions can then be systematically investigated, validating the theoretical framework and identifying potential limitations of either approach. This combined methodology offers a higher degree of confidence in the characterization of the system’s behavior near critical points than either method alone.
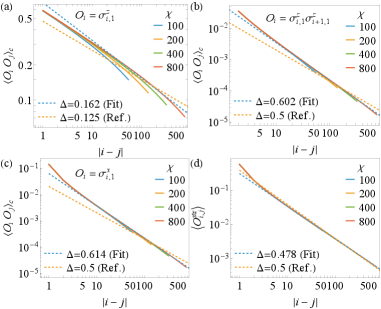
Mapping to Universal Principles: The Power of Conformal Field Theory
Recent investigations into the N-Coupled Ising Chain model reveal a compelling correspondence with the frameworks of Conformal Field Theory (CFT). Specifically, the model’s behavior near critical points aligns remarkably well with predictions from Ising CFT, a well-established theory describing systems undergoing continuous phase transitions. Furthermore, under certain conditions – notably, when the coupling strength ‘N’ increases – the model exhibits characteristics describable by the more complex SO(N)1 Wess-Zumino-Witten (WZW) CFT. This theoretical equivalence isn’t merely a mathematical curiosity; it provides a robust methodology for analyzing the Ising Chain model’s critical exponents and correlation functions, offering precise predictions about its behavior. The ability to map a seemingly simple chain of interacting spins onto the language of CFT opens avenues for understanding its fundamental properties and offers a pathway to explore connections with diverse physical systems exhibiting similar critical phenomena, from magnetism to polymer physics.
The demonstrated equivalence between the N-Coupled Ising Chain model and conformal field theories – specifically Ising CFT and, in some instances, the SO(N)1 WZW CFT – offers a significantly enhanced capacity for analyzing the model’s critical behavior. This connection isn’t merely descriptive; it allows researchers to leverage the well-established mathematical framework of CFT to predict properties that would otherwise be difficult or impossible to determine directly. By mapping the Ising Chain onto the language of conformal field theory, calculations involving correlation functions, critical exponents, and scaling laws become tractable, providing precise quantitative predictions about the system’s behavior near its critical point. This predictive power extends beyond simply confirming existing knowledge; it enables the exploration of previously inaccessible regimes and the identification of novel phenomena within the N-Coupled Ising Chain model, effectively transforming a complex physical system into a playground for theoretical investigation.
The analytical connections established between the N-Coupled Ising Chain model and conformal field theories extend beyond this specific system, offering valuable insights into a diverse array of physical phenomena. Many materials undergoing continuous phase transitions – from magnetic systems to liquid crystals and even certain polymer configurations – exhibit critical behavior governed by universal principles. The mathematical tools and techniques developed to understand the Ising Chain, particularly its connection to SO(N)1 WZW CFT, provide a framework for characterizing the critical exponents and scaling laws observed in these seemingly disparate materials. This allows researchers to predict the behavior of complex systems near their critical points, offering a powerful means to classify and understand phase transitions more generally, and potentially guiding the development of new materials with tailored properties.
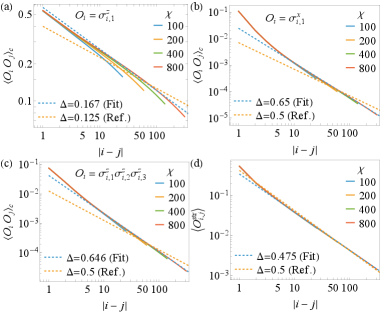
The study meticulously charts phase transitions in coupled Ising chains, revealing a nuanced interplay between symmetry and topology. It demonstrates how conjectures about continuous transitions can falter when confronted with rigorous analysis – a stark reminder that predictive power is not causality. This echoes John Stuart Mill’s observation that ‘It is better to be a dissatisfied Socrates than a satisfied fool,’ as the researchers actively disprove existing beliefs about symmetry-protected topological phases instead of simply accepting them. The investigation’s findings, particularly the shift to first-order transitions for N≥4, highlight the importance of embracing uncertainty and continually testing hypotheses – a process driven by failure, not confirmation.
Where Do the Breaks Show?
The insistence on continuous transitions, particularly into symmetry-protected topological phases, has long felt more like an aesthetic preference than a rigorously defended position. This work, demonstrating first-order transitions for N≥4, doesn’t so much disprove earlier conjectures as illuminate their limited domain of validity. The field has, for too long, prioritized finding the elegant solution over mapping the boundaries of its failure. It is in these failures-these breaks in the expected-that genuine progress resides.
Future investigations should, predictably, focus on extending these results to more complex systems. However, a more fruitful avenue may lie in a systematic study of why these transitions behave as they do. What precisely is lost-or gained-when the continuous path bifurcates? The exploration of finite-size effects, and the development of more robust analytical techniques capable of handling strong coupling regimes, are not merely technical challenges, but essential steps toward a less optimistic, and therefore more accurate, understanding.
Ultimately, the value of this work isn’t in providing answers, but in refining the questions. The pursuit of topological order has, at times, resembled an exercise in wishful thinking. Perhaps it is time to accept that nature isn’t obligated to conform to one’s preferred symmetry, and to embrace the messy, unpredictable reality that lies beyond the idealized models.
Original article: https://arxiv.org/pdf/2602.17029.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- Poppy Playtime Chapter 5: Engineering Workshop Locker Keypad Code Guide
- Jujutsu Kaisen Modulo Chapter 23 Preview: Yuji And Maru End Cursed Spirits
- God Of War: Sons Of Sparta – Interactive Map
- 8 One Piece Characters Who Deserved Better Endings
- Who Is the Information Broker in The Sims 4?
- Mewgenics Tink Guide (All Upgrades and Rewards)
- Pressure Hand Locker Code in Poppy Playtime: Chapter 5
- Poppy Playtime Chapter 5: Emoji Keypad Code in Conditioning
- Poppy Playtime 5: Battery Locations & Locker Code for Huggy Escape Room
- I Used Google Lens to Solve One of Dying Light: The Beast’s Puzzles, and It Worked
2026-02-21 11:10