Author: Denis Avetisyan
A new analysis reveals that the Low-Rank Adaptation (LoRA) technique, combined with strategic noise addition, can offer stronger privacy guarantees than previously understood.
This research demonstrates privacy amplification in LoRA through the interplay of noise and the inherent randomness of its projection mechanism, offering a new approach to matrix privacy.
While the increasing use of low-rank adaptation (LoRA) in machine learning suggests potential privacy benefits from inherent randomness, this is often a misleading assumption. Our work, ‘LoRA and Privacy: When Random Projections Help (and When They Don’t)’, analyzes the differential privacy properties of LoRA through the lens of Wishart projections, revealing that noise-free LoRA is, in fact, not inherently private. We demonstrate that combining noise with this projection mechanism amplifies privacy beyond standard calibration techniques, yet also establish sharp limitations on privacy guarantees in certain settings. Can a deeper understanding of these randomized projections unlock more effective and efficient privacy-preserving machine learning strategies?
Unveiling the Privacy Paradox of Efficient Adaptation
While parameter-efficient fine-tuning (PEFT) techniques, such as Low-Rank Adaptation (LoRA), are gaining prominence for their computational efficiency and storage benefits, they inadvertently create novel privacy risks. These methods achieve performance gains by updating only a small fraction of a pre-trained model’s parameters, a strategy that, counterintuitively, can still expose sensitive information present in the training data. The reduced dimensionality of the updated parameters, rather than providing inherent privacy, can function as a leakage channel, allowing adversaries to reconstruct details about individual data points used during fine-tuning. This vulnerability arises because the changes to these limited parameters encode information about the specific training examples that drove those adjustments, presenting a significant challenge to maintaining data confidentiality when deploying these increasingly popular machine learning approaches.
Despite the efficiency gains, parameter-efficient tuning methods like Low-Rank Adaptation (LoRA) don’t inherently safeguard training data privacy. The core principle of updating only a small subset of model parameters, while computationally advantageous, creates a potential leakage pathway. Studies demonstrate that even these limited parameter changes can encode information about individual data points used during fine-tuning. This occurs because the adapted parameters effectively ‘memorize’ characteristics of the training set, and attackers can exploit these subtle changes to infer whether a specific data sample was included in the training process. Consequently, the very mechanism that makes LoRA efficient – focusing on a limited parameter space – paradoxically introduces new vulnerabilities regarding data privacy, necessitating the development of robust privacy-preserving techniques tailored to these methods.
The application of traditional Differential Privacy (DP) to modern, large-scale models faces substantial hurdles. While DP offers a robust mathematical framework for privacy, its effectiveness relies on careful calibration of the privacy loss parameter, ε, which dictates the trade-off between privacy and utility. Achieving this calibration becomes increasingly complex with the sheer number of parameters in contemporary models and the expansive datasets used for training. Furthermore, the computational cost of DP mechanisms-such as adding noise to gradients-scales unfavorably with model size and dataset volume, potentially rendering them impractical for resource-constrained environments. This necessitates exploration of alternative privacy-preserving techniques or more efficient implementations of DP that can effectively safeguard sensitive information without crippling model performance or incurring prohibitive computational overhead.
Recent studies demonstrate that models refined using Low-Rank Adaptation (LoRA) are surprisingly vulnerable to Membership Inference Attacks. These attacks aim to determine whether a specific data point was used during the model’s training process, and they prove remarkably effective against LoRA-tuned models. Researchers found that, with a rank of 128 or higher, these attacks achieve perfect accuracy in identifying member data – meaning an attacker can reliably confirm if a given sample influenced the model’s learning. This heightened vulnerability stems from the fact that, while LoRA reduces the number of trainable parameters, the retained information within those parameters can still be exploited to reveal sensitive training data. The findings underscore a critical need for enhanced privacy safeguards when deploying parameter-efficient fine-tuning techniques, particularly as these methods become increasingly prevalent in machine learning applications.
Wishart Projection: Reclaiming Privacy Through Dimensionality
Wishart Projection is a dimensionality reduction technique building upon the principles of Random Projection, but incorporates properties designed to enhance data privacy. While Random Projection transforms high-dimensional data into a lower-dimensional space using randomly generated matrices, Wishart Projection utilizes matrices generated from Wishart distributions. This process introduces specific statistical properties-namely, eigenvalues and eigenvectors with predictable distributions-that are advantageous when combined with differential privacy mechanisms. The use of Wishart matrices allows for a controlled reduction in dimensionality while preserving data characteristics critical for minimizing information leakage, potentially leading to improved privacy-utility trade-offs compared to standard Random Projection approaches.
Pre-processing data with dimensionality reduction via projection before the application of privacy mechanisms, such as differential privacy, can enhance privacy guarantees by reducing the sensitivity of the data to individual records. This is because the projection process effectively reduces the influence of any single data point on the overall result of the privacy mechanism. Specifically, by mapping high-dimensional data to a lower-dimensional space, the magnitude of change resulting from modifying a single record is lessened, thus decreasing the privacy loss incurred by the mechanism. The effectiveness of this approach depends on the projection method and its ability to preserve the essential information while obscuring individual contributions, allowing for a more robust privacy-utility trade-off.
Wishart Projection utilizes the statistical properties of Wishart matrices – random matrices derived from the covariance of a Gaussian process – to achieve improved privacy-utility trade-offs in dimensionality reduction. Specifically, the spectral properties of Wishart matrices, notably their predictable distribution of eigenvalues, enable a controlled reduction in dimensionality while preserving key data characteristics. This controlled reduction, prior to the application of differential privacy or other privacy-enhancing technologies, demonstrably amplifies privacy guarantees. Theoretical analysis indicates that the privacy loss incurred during projection is reduced due to the matrix’s structure, allowing for stronger privacy parameters – such as a smaller epsilon value in differential privacy – while maintaining acceptable data utility compared to standard random projections. The degree of amplification is directly related to the dimensions of the original and projected spaces and the specific properties of the Wishart matrix employed.
The performance of Wishart Projection is contingent on the characteristics of the input data and the degree of adversarial alignment present. AdversarialAlignment refers to the scenario where an attacker possesses prior knowledge regarding the data distribution and can strategically position data points in the input space to maximize information leakage after dimensionality reduction and privacy mechanism application. Specifically, if data exhibits strong alignment with the principal components of the Wishart matrix used for projection, the privacy guarantees offered by the technique are diminished. Conversely, data that is less aligned, or randomly distributed, benefits more significantly from the privacy amplification offered by Wishart Projection. Therefore, assessing and mitigating potential AdversarialAlignment is crucial for effectively deploying this technique and ensuring robust privacy protection.
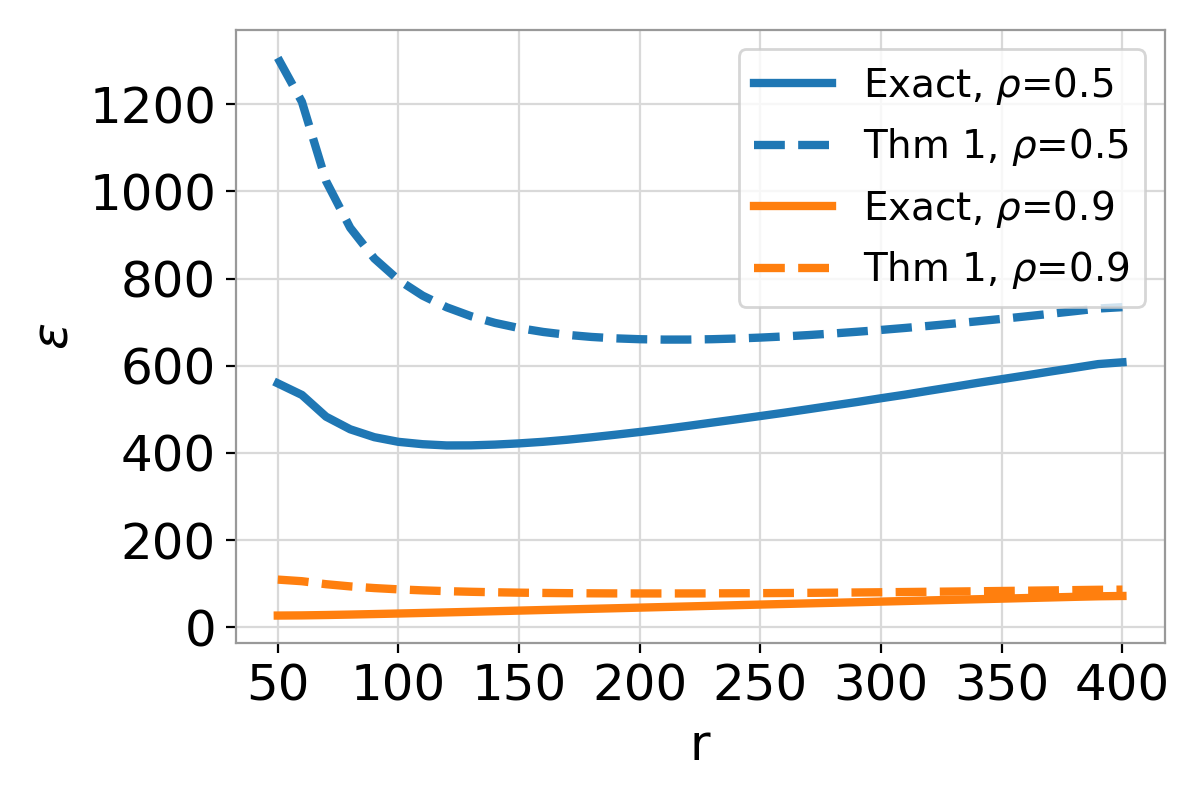
Noise Injection Strategies: M1 Versus M2
Two distinct strategies, designated M1 and M2, were examined for the injection of noise during the privacy-preserving process. M1 implements noise addition following the Wishart projection, a common approach in differential privacy mechanisms. Conversely, M2 applies noise addition prior to the Wishart projection. Both methods leverage a GaussianMechanism to introduce randomness, ensuring adherence to differential privacy principles. The core distinction lies in the temporal order of these operations-whether the randomization occurs before or after the dimensionality reduction inherent in the Wishart projection-and this sequencing demonstrably impacts the resulting privacy guarantees, as detailed in subsequent analyses.
The GaussianMechanism is a widely employed technique for achieving differential privacy by adding random noise drawn from a Gaussian distribution to a query’s output. This mechanism operates by calibrating the noise scale to the sensitivity of the query – the maximum amount the query’s result can change with a single individual’s data altered. Specifically, noise is sampled from a normal distribution with a mean of zero and a standard deviation proportional to the global sensitivity divided by the privacy parameter ε. The magnitude of this standard deviation directly controls the privacy-utility trade-off; larger deviations provide stronger privacy guarantees but reduce data utility, while smaller deviations offer increased utility at the cost of weaker privacy. The use of a Gaussian distribution simplifies analysis and provides well-understood privacy bounds.
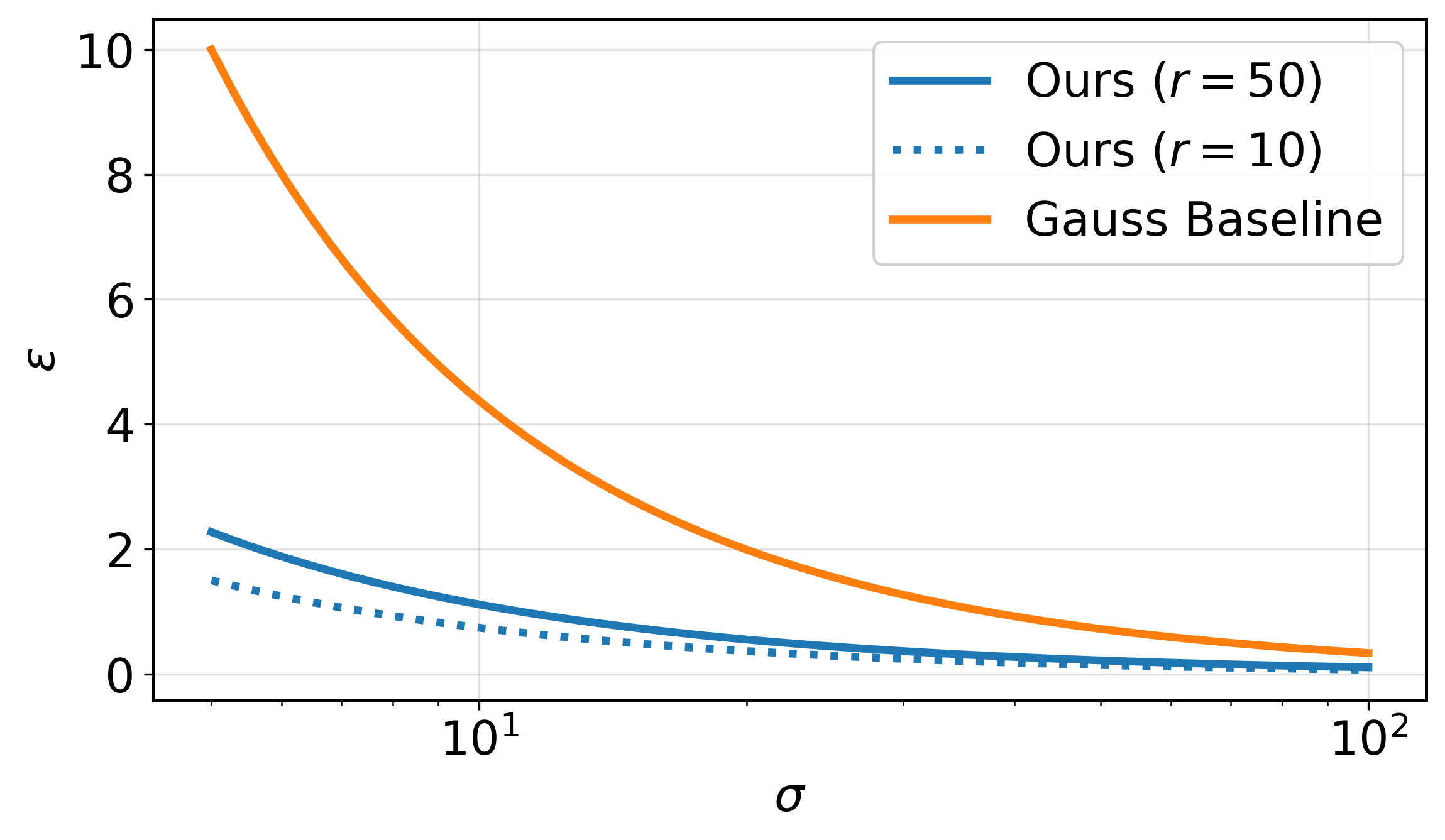
Empirical evaluation indicates that the M2 noise addition strategy, which injects Gaussian noise prior to the Wishart projection, achieves superior privacy amplification compared to standard additive noise baselines when the rank r is significantly smaller than the data dimension d (i.e., r << d). Specifically, M2 consistently demonstrates a reduction in the overall privacy loss parameter ε across a range of experimental settings. This improvement is quantifiable through direct comparison of ε values obtained with M2 versus those from standard noise addition techniques, consistently showing lower values for M2 in the small-rank regime. These results are based on repeated experiments and statistical analysis of privacy loss calculations.
The privacy amplification observed with M2-noise addition prior to the Wishart projection-arises from a non-trivial interaction between the random noise and the dimensionality reduction process. Unlike standard noise addition methods where privacy loss is directly calibrated to the noise scale, the Wishart projection alters the statistical properties of the data before noise is applied. This alteration effectively reshapes the sensitivity of the query, leading to a reduced overall privacy loss ε compared to adding noise to the unprojected data. The projection concentrates the data’s variance onto fewer dimensions, and the subsequent noise addition then operates on this concentrated distribution, creating a stronger privacy guarantee than would be achieved with equivalent noise applied to the original, higher-dimensional data.
The Implications of Secure Adaptation
The demonstrated vulnerabilities within Low-Rank Adaptation (LoRA), a popular parameter-efficient fine-tuning technique, carry substantial implications for the field of privacy-preserving machine learning, especially as large language models (LLMs) become increasingly prevalent. Because LoRA, in its standard implementation, does not inherently guarantee differential privacy, sensitive information embedded within training data remains potentially accessible through model updates – a critical concern given the scale and data-hungry nature of LLMs. This research highlights the necessity for careful consideration of such parameter-efficient methods and motivates the development of robust privacy mechanisms specifically tailored to these techniques, ensuring that the benefits of efficient learning do not come at the expense of user privacy. The findings underscore a need to move beyond simply applying traditional privacy methods and instead focus on vulnerabilities unique to these adaptive training approaches.
Despite the computational advantages of Low-Rank Adaptation (LoRA), particularly its use of MatrixValuedUpdates, recent analyses reveal inherent privacy vulnerabilities. While LoRA reduces the number of trainable parameters, it does not, in its standard form, offer differential privacy; noise-free implementations are demonstrably susceptible to privacy attacks. This arises because the low-rank updates, while efficient, still leak information about the original training data through the adapted weights. Consequently, researchers must carefully consider and implement robust mitigation strategies – such as the addition of carefully calibrated noise – to safeguard sensitive information when deploying LoRA in privacy-critical applications. Addressing these vulnerabilities is crucial for realizing the full potential of efficient adaptation techniques without compromising data privacy.
Further research endeavors are directed towards refining the Wishart projection and noise addition techniques to enhance their efficacy across diverse datasets and model designs. Current strategies assume a degree of data homogeneity that may not always hold true in real-world applications; therefore, adaptive noise calibration based on the underlying data distribution is a key area of investigation. Specifically, researchers aim to develop noise schedules that balance privacy guarantees with minimal impact on model utility, tailoring the level of perturbation to the sensitivity of different model parameters and data characteristics. Optimizing the Wishart projection-a computationally intensive step-for specific model architectures, such as transformers and recurrent neural networks, will also be crucial for scalability and practical deployment of privacy-preserving machine learning systems.
The development of privacy-preserving machine learning techniques stands as a crucial advancement in an era increasingly reliant on data-driven systems. This research, by directly addressing vulnerabilities within efficient adaptation methods like LoRA, contributes a tangible step towards realizing that goal. While challenges remain in fully mitigating privacy risks and optimizing performance, the approach demonstrates a pathway for building machine learning models that can learn from sensitive data without compromising individual privacy. Further refinement of noise addition and projection strategies promises to enhance both the robustness and practical applicability of these systems, potentially unlocking broader adoption across various domains requiring secure and responsible data handling.
The exploration within this paper doesn’t simply accept LoRA as a privacy risk; it actively investigates how inherent randomness, specifically the Wishart projection, interacts with added noise. This mirrors a core tenet of truly understanding any system-dissection, not dismissal. As Edsger W. Dijkstra observed, “In moments of decision, the best thing you can do is the right thing; the next best thing is the wrong thing.” The researchers, in a sense, tested the ‘wrong thing’ – noise addition – to discover amplified privacy beyond expectations. This isn’t about eliminating vulnerabilities, but about leveraging the system’s properties, like the projection mechanism, to unexpectedly strengthen defense, turning a potential weakness into a source of resilience. The study demonstrates that privacy isn’t always a matter of perfect shielding, but a delicate balance of understanding and controlled exposure.
What’s Next?
The apparent paradox-that a structured, low-rank adaptation technique requires noise to achieve meaningful privacy-should give anyone calibrating a differential privacy budget pause. It suggests the entire endeavor is less about preventing information leakage and more about strategically obscuring it. The paper demonstrates a fortuitous alignment between projection randomness and noise amplification, but this feels less like a fundamental principle and more like exploiting a quirk of linear algebra. Future work should investigate whether similar “accidental” privacy benefits exist in other parameter-efficient fine-tuning methods, or if LoRA represents a special case.
A crucial limitation remains the reliance on Gaussian noise. The choice of noise distribution feels… convenient. Real-world adversaries rarely adhere to statistical assumptions. Exploring non-Gaussian noise models-perhaps those mirroring the statistical properties of the training data itself-could reveal vulnerabilities currently hidden by the neatness of theoretical analysis. Moreover, the adversarial privacy landscape is perpetually shifting. The current focus on gradient leakage overlooks subtler attacks – those targeting the structure of the adapted parameters, rather than their precise values.
Ultimately, this work isn’t a solution, but a provocation. It highlights the uncomfortable truth that privacy isn’t a property of an algorithm, but a fragile equilibrium maintained against a relentlessly inventive opponent. The field should abandon the pursuit of “privacy by design” and embrace a more honest approach: “privacy by constant adversarial testing.”
Original article: https://arxiv.org/pdf/2601.21719.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- Gold Rate Forecast
- How to Unlock the Mines in Cookie Run: Kingdom
- How to Find & Evolve Cleffa in Pokemon Legends Z-A
- Jujutsu: Zero Codes (December 2025)
- Gears of War: E-Day Returning Weapon Wish List
- The Saddest Deaths In Demon Slayer
- Most Underrated Loot Spots On Dam Battlegrounds In ARC Raiders
- Top 8 UFC 5 Perks Every Fighter Should Use
- Epic Pokemon Creations in Spore That Will Blow Your Mind!
- Bitcoin Frenzy: The Presales That Will Make You Richer Than Your Ex’s New Partner! 💸
2026-02-01 22:27