Author: Denis Avetisyan
Researchers demonstrate that utilizing qutrits – quantum systems with three levels – can offer advantages in implementing the Harrow-Hassidim-Lloyd algorithm for solving linear equations, a core component of many quantum simulations.
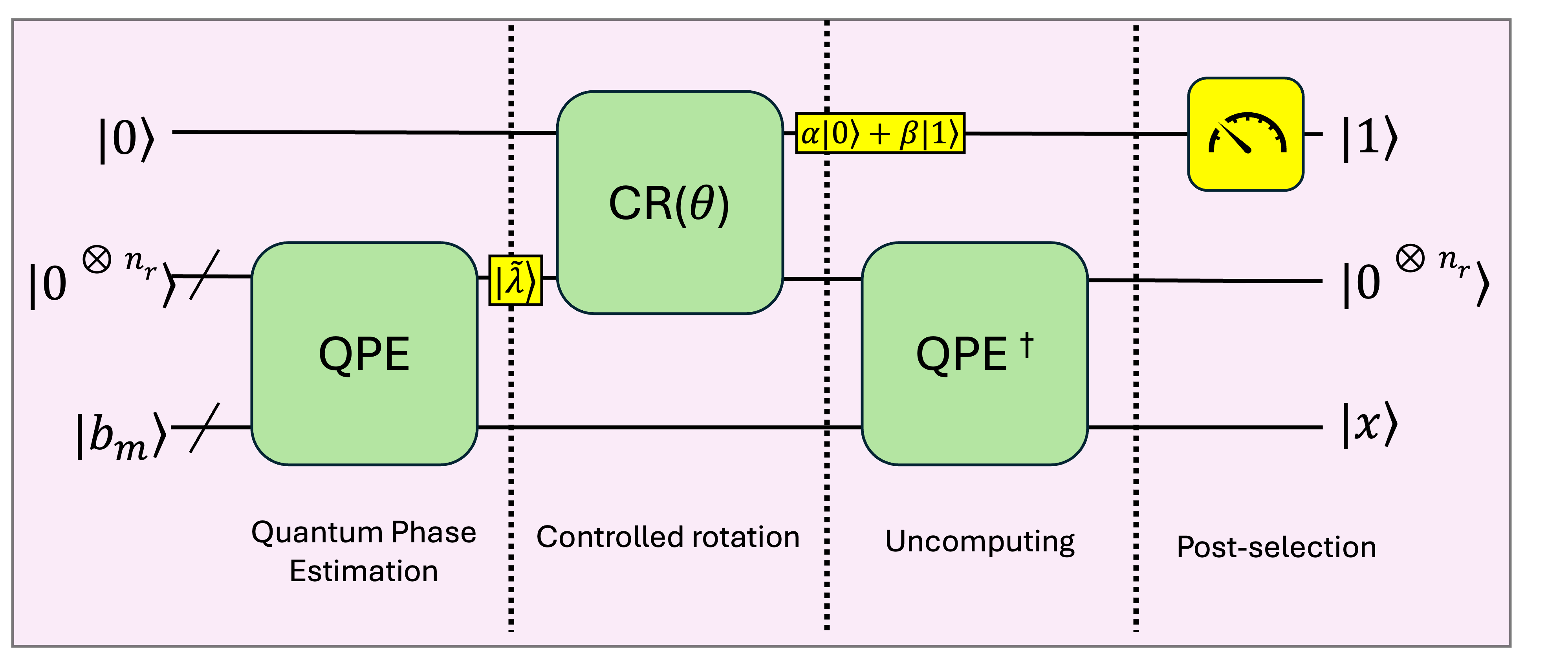
This work extends the HHL algorithm to qutrits, potentially reducing qudit requirements for quantum chemistry applications while maintaining comparable gate complexity.
Solving linear systems of equations is a fundamental task in many scientific domains, yet classical algorithms can struggle with increasingly complex problems. This work extends the Harrow-Hassidim-Lloyd (HHL) algorithm, a quantum approach to linear equation solving, to utilize qutrits – quantum systems with three levels – instead of the traditional qubit framework. We demonstrate that a qutrit-based HHL implementation can achieve a reduction in the number of required quantum digits while maintaining a comparable number of quantum gate operations, particularly beneficial for applications like quantum chemistry and potential energy curve calculations. Could this qutrit advantage pave the way for more efficient quantum simulations of complex molecular systems?
The Emergence of Complexity: A Computational Bottleneck
The pursuit of novel materials and effective pharmaceuticals relies heavily on the ability to accurately simulate molecular behavior. However, a fundamental challenge arises from the exponential increase in computational demand as the size of the modeled system grows. This isn’t merely a matter of needing faster computers; the underlying mathematical complexity of describing interactions between many electrons scales unfavorably with each added atom. For instance, simulating a molecule with $n$ atoms requires computational resources that grow proportionally to $n^k$, where $k$ is often greater than 3, quickly exceeding the capacity of even the most powerful supercomputers. Consequently, the complexity limits the achievable size and accuracy of simulations, hindering progress in fields where predictive molecular modeling is paramount – from designing superconductors to discovering life-saving drugs.
Highly accurate computational methods, such as Linearized Coupled Cluster (LCC), excel at describing the electronic structure of simple molecular systems-the hydrogen molecule ($H_2$) serves as a prime example-by effectively accounting for electron correlation. However, the computational demands of LCC scale exponentially with the number of electrons and atomic orbitals, quickly rendering it impractical for all but the smallest molecules. This limitation arises from the need to consider an enormous number of possible electron interactions, a combinatorial problem that overwhelms even the most powerful supercomputers when applied to systems containing just a few dozen atoms. Consequently, while LCC provides a benchmark for accuracy, its intractability motivates the ongoing search for alternative, scalable computational techniques in quantum chemistry.
A comprehensive understanding of molecular dynamics relies heavily on the accurate calculation of Potential Energy Curves (PECs), which map the energy of a molecule as its geometry changes. However, traditional computational methods face a significant hurdle: the computational cost of determining these curves scales exponentially with the number of atoms involved. This means that while PECs can be reliably calculated for simple systems like diatomic molecules, extending these calculations to larger, more complex molecules – crucial for modeling realistic materials or biological processes – quickly becomes intractable. The challenge isn’t simply a matter of needing faster computers; it’s a fundamental limitation of the algorithms themselves, demanding innovative approaches to efficiently approximate molecular energies across a vast conformational space. Consequently, researchers are actively exploring methods to reduce this computational burden, seeking ways to accurately model molecular behavior without being limited by the exponential scaling of classical techniques, and ultimately unlocking the potential for in silico material design and drug discovery.
Harnessing Quantum Mechanics: A Path Towards Scalability
The Harrow-Hassidim-Lloyd (HHL) algorithm presents a potential exponential speedup for solving systems of linear equations, a core computational task in many quantum chemistry applications. Classical algorithms typically require $O(N^3)$ operations for solving a system of $N$ equations, whereas HHL, under specific conditions, achieves a complexity of $O(log(N))$. This advantage stems from the algorithm’s ability to leverage quantum superposition and interference. Specifically, HHL efficiently encodes the linear system as a Hamiltonian, then uses quantum phase estimation to determine eigenvalues related to the solution, and finally employs a quantum inverse to extract the solution vector. The practical realization of this speedup hinges on the ability to efficiently prepare the input quantum state and perform the required quantum operations with sufficient fidelity, as well as the condition that the linear system is well-conditioned.
The application of the Harrow-Hassidim-Lloyd (HHL) algorithm to molecular systems necessitates the translation of classical molecular data into quantum states represented by qubits. This encoding process involves mapping molecular properties, such as Hamiltonian matrices and wavefunctions, onto the Hilbert space of the quantum computer. While qubits, representing two-level quantum systems, are commonly used, qudits – quantum systems with d > 2 levels – offer potential advantages in certain encodings by allowing for more compact representations of data, potentially reducing the number of qubits required and mitigating decoherence effects. The efficiency of the HHL algorithm is directly dependent on the fidelity of this initial state preparation and the effective representation of the molecular Hamiltonian as a sparse matrix, $A$, to enable efficient application of the quantum operators.
The Harrow-Hassidim-Lloyd (HHL) algorithm leverages the Quantum Phase Estimation (QPE) and Quantum Fourier Transform (QFT) algorithms to efficiently estimate the eigenvalues of a Hermitian matrix, which is a crucial step in solving linear systems of equations. QPE, operating on an eigenstate $|\psi\rangle$, estimates its phase $e^{2\pi i \phi}$ with precision $\epsilon$ using a controlled unitary operation and inverse Quantum Fourier Transform. The QFT, a quantum analogue of the Discrete Fourier Transform, efficiently transforms between the computational basis and the phase basis, facilitating the phase estimation process. The accuracy of the phase estimation, and therefore the solution to the linear system, scales polynomially with the desired precision and the condition number of the matrix, offering a potential exponential speedup over classical algorithms for specific problem instances.
Expanding Computational Horizons: Qudits and Ternary Logic
Qudits, representing an extension of the qubit by utilizing a three-level system instead of two, enhance the information density and computational capabilities of the Harrow-Hassidim-Lloyd (HHL) algorithm. While a qubit can represent $2^1$ states, a qudit can represent $3^1$ states, and $n$ qudits can represent $3^n$ states compared to $2^n$ for qubits. This increased representational capacity directly translates to a more efficient encoding of information within the HHL algorithm, particularly in the clock register required for scaling the quantum computation. The use of qudits allows for a reduction in the number of physical qudits needed to achieve a comparable level of precision in the HHL algorithm compared to qubit-based implementations.
Ternary logic, employing three distinct states – typically represented as 0, 1, and 2 – provides a more expressive computational basis than the binary logic underpinning traditional qubits. While qubits utilize two states allowing for $2^n$ possible values with n qubits, qudits leveraging ternary logic allow for $3^n$ possible values with n qudits. This increased representational capacity directly translates to a more efficient encoding of information and potentially reduces the resources required to perform complex computations. The expanded state space enables more compact representations of mathematical operations and algorithms, as fewer qudits are needed to achieve the same level of precision compared to qubit-based systems.
The extension of the Harrow-Hassidim-Lloyd (HHL) algorithm to utilize qutrits – three-level quantum digits – results in a quantifiable reduction in resource requirements. Specifically, implementation with qutrits lowers the number of qudits necessary in the clock register by a factor of $log_2(3) \approx 0.63$ compared to traditional qubit-based HHL algorithms, while maintaining equivalent computational precision. This reduction stems from the increased information density afforded by the ternary nature of qutrits, allowing for more efficient representation of algorithmic parameters within the clock register and consequently minimizing the required quantum resources.
Implementation of the HHL algorithm utilizing qudits, specifically qutrits, demonstrates a significant reduction in required quantum gates. Analysis indicates a 39% decrease in 2-qudit gates within the Quantum Fourier Transform (QFT) module when compared to qubit-based HHL implementations. This gate reduction stems from the increased information density of qudits, allowing for more efficient representation and manipulation of data within the algorithm’s computational processes. The improvement directly impacts resource requirements and potential scalability of the HHL algorithm on quantum hardware.
The implementation of quantum algorithms such as the Harrow-Hassidim-Lloyd (HHL) algorithm relies on specialized quantum registers to manage and store intermediate computational results. The HHL algorithm, used for solving linear systems of equations, requires a Clock Register to track the number of iterations and control the precision of the solution, and a State Register to store the quantum state representing the solution vector. These registers are distinct from the input and output registers and are crucial for the algorithm’s functionality; their size directly impacts the quantum resource requirements and overall computational cost. Efficient utilization of these registers, through techniques like optimized state preparation and measurement strategies, is essential for realizing practical quantum advantage with algorithms like HHL.
Unlocking Predictive Power: Towards Accurate Molecular Simulations
Within the landscape of quantum simulation, achieving a practical balance between computational expense and accuracy remains a central challenge. Local Coupled Cluster Doubles (LCCSD) represents a sophisticated approximation method designed to address this need, building upon the foundations of Guided Unitary Group Approximation – Configuration Interaction Singles and Doubles (GUGA-CISD). This iterative refinement of the quantum state allows for the efficient calculation of molecular correlation energy – the energy resulting from the interactions between electrons – while significantly reducing the computational resources required compared to full configuration interaction methods. When integrated with the Harrow-Hassidim-Lloyd (HHL) algorithm, LCCSD leverages quantum speedups to tackle complex molecular systems previously beyond the reach of classical computation, offering a pathway towards simulating larger and more realistic chemical processes.
The Harrow-Hassidim-Lloyd (HHL) algorithm, a cornerstone of quantum computation for linear systems of equations, doesn’t operate on bits like classical computers, but rather manipulates the probability amplitudes of quantum states. This is achieved through a carefully orchestrated sequence of controlled rotation and two-qudit gate operations. Controlled rotations precisely alter the quantum state based on the input data, effectively encoding the problem into the quantum system. Subsequently, two-qudit gates, acting on pairs of quantum digits (qudits), perform the core computational steps – analogous to matrix operations in classical computation – leveraging quantum entanglement and superposition to explore solution spaces far more efficiently. The precision of these gate operations is critical, as even slight errors can propagate and invalidate the final result; however, the potential for exponential speedups over classical algorithms makes this approach a promising pathway for solving complex scientific challenges.
Recent investigations into molecular simulations demonstrate the remarkable precision of the qutrit HHL-LCCSD approach when calculating correlation energy. Specifically, this method achieves an accuracy within 0.02% of the established benchmark provided by classical LCCSD calculations for the hydrogen molecule ($H_2$). This near-equivalence is significant because it validates the potential of combining quantum algorithms, like the HHL algorithm, with sophisticated approximation techniques to deliver results comparable to traditional, computationally intensive methods. The ability to accurately model correlation energy-a crucial component in determining molecular properties and reaction dynamics-with such high fidelity opens avenues for simulating larger, more complex molecular systems previously considered beyond reach.
Molecular simulations, crucial for fields ranging from materials science to drug discovery, often face limitations due to the exponential scaling of computational cost with system size. However, the synergy between advanced approximation methods and the Harrow-Hassidim-Lloyd (HHL) algorithm presents a pathway to overcome these challenges. By intelligently reducing the complexity of molecular calculations – utilizing techniques like coupled cluster theory – and then leveraging the HHL algorithm’s potential for quantum speedup, researchers can address simulations previously considered computationally intractable. This combination allows for more accurate modeling of complex molecular interactions and properties, potentially accelerating the design of novel materials and pharmaceuticals by unlocking insights unavailable through classical computation alone. The promise lies in shifting the boundary of what is computationally feasible, opening doors to a deeper understanding of the molecular world.
The exploration of qutrit-based systems, as detailed in this work, underscores a principle resonant with complex systems theory. Rather than imposing a hierarchical structure to solve linear equations-a top-down approach-the research suggests benefits from leveraging the inherent properties of a more nuanced quantum substrate. As John Bell keenly observed, “No physical theory can predict everything.” This echoes the idea that attempting to rigidly define outcomes in quantum chemistry-or any complex simulation-is often less fruitful than allowing solutions to emerge from the interplay of local rules, as demonstrated by the HHL algorithm’s extension to qutrits. The reduction in required qudits, while maintaining comparable gate counts, isn’t a matter of control, but of influencing the system to find efficient pathways to a solution.
Beyond the Qudit: Future Directions
The extension of the Harrow-Hassidim-Lloyd algorithm to qutrits, as demonstrated, isn’t a revolution, but a logical progression. Global regularities emerge from simple rules, and the search for efficient representations of linear systems will invariably explore higher-dimensional qudits. The immediate challenge isn’t merely scaling to larger systems-that’s a constant companion in any computational endeavor-but understanding the inherent trade-offs between qudit dimension, gate complexity, and the structure of the problem itself. A reduction in qudit count, while appealing, is meaningless if the required controlled rotations become exponentially more difficult to implement.
The focus will likely shift from simply finding speedups to understanding where these algorithms truly excel. Quantum chemistry, with its inherent symmetries and sparse Hamiltonians, appears a promising domain, but a broader exploration of problem classes is crucial. Any attempt at directive management often disrupts this process, and a rigid adherence to specific applications may stifle the discovery of unanticipated efficiencies. The algorithm’s utility isn’t predetermined; it will be revealed through its interaction with the computational landscape.
Ultimately, the question isn’t whether qutrits-or higher-dimensional analogues-will surpass qubits, but whether the pursuit of more efficient representations will lead to genuinely novel computational paradigms. The algorithm is a tool, and its value will be determined not by its theoretical potential, but by the emergent properties of the systems it allows us to explore.
Original article: https://arxiv.org/pdf/2511.17960.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- Rebecca Heineman, Co-Founder of Interplay, Has Passed Away
- Best Build for Operator in Risk of Rain 2 Alloyed Collective
- 9 Best In-Game Radio Stations And Music Players
- Top 15 Best Space Strategy Games in 2025 Every Sci-Fi Fan Should Play
- ADA PREDICTION. ADA cryptocurrency
- USD PHP PREDICTION
- The 20 Best Real-Time Strategy (RTS) Games Ever You Must Play!
- All Exploration Challenges & Rewards in Battlefield 6 Redsec
- OKB PREDICTION. OKB cryptocurrency
- BCH PREDICTION. BCH cryptocurrency
2025-11-26 01:00