Beyond Reversibility: Rewriting Gravity with Quantum Circuits

Author: Denis Avetisyan

New research explores how non-invertible symmetries in quantum circuits connect to the geometry of gravity, potentially refining our understanding of the AdS/CFT correspondence.

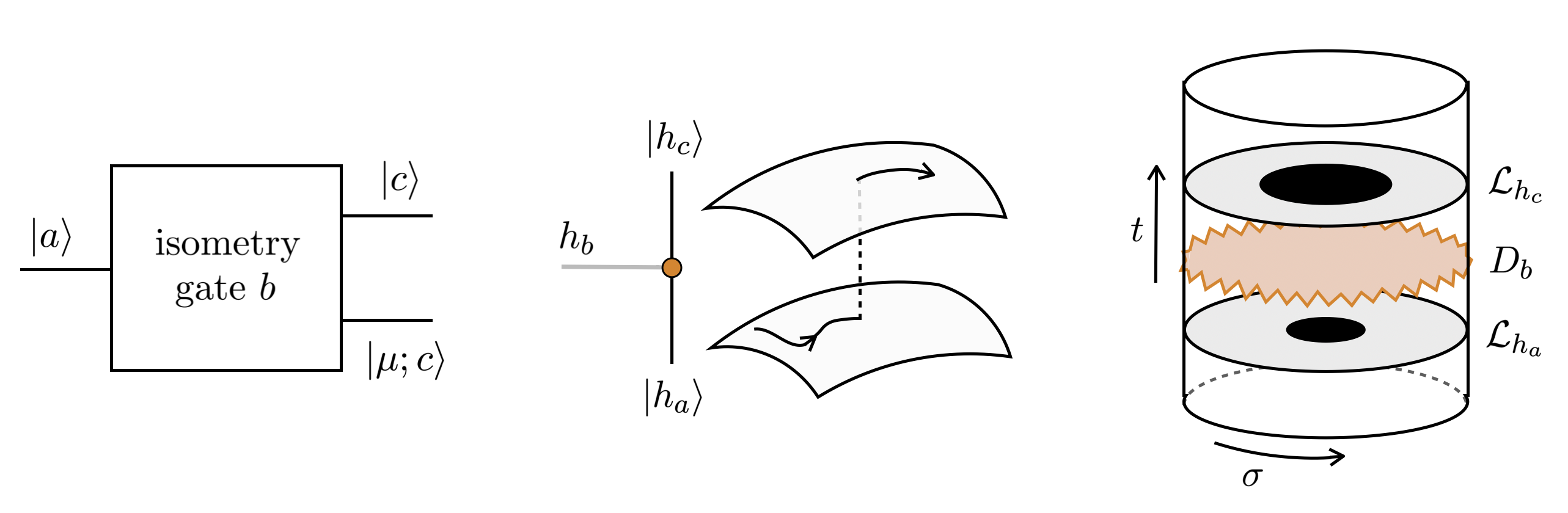
The study demonstrates that a non-invertible fusion gate operates not as a continuous transformation-such as movement along a Virasoro coadjoint orbit-but as a discrete shift between conformal families characterized by distinct conformal weights <span class="katex-eq" data-katex-display="false">h_a, h_b, h_c</span>, effectively manifesting in an AdS3/CFT correspondence as an instantaneous insertion of a defect <span class="katex-eq" data-katex-display="false">D_b</span> that abruptly alters boundary stress-tensor data and delineates regions governed by differing highest-weight representations. — The study demonstrates that a non-invertible fusion gate operates not as a continuous transformation-such as movement along a Virasoro coadjoint orbit-but as a discrete shift between conformal families characterized by distinct conformal weights $h_a, h_b, h_c$ , effectively manifesting in an AdS3/CFT correspondence as an instantaneous insertion of a defect $D_b$ that abruptly alters boundary stress-tensor data and delineates regions governed by differing highest-weight representations.

This paper extends quantum circuit complexity to incorporate non-invertible symmetries arising from fusion rules in conformal field theory and investigates their implications for 3d Ising gravity.

Standard formulations of quantum circuit complexity rely on invertible operations, restricting the exploration of transitions between distinct symmetry sectors in systems like two-dimensional conformal field theories. This work, ‘Non-invertible Nielsen circuits and 3d Ising gravity’, extends Nielsen’s circuit framework to incorporate intrinsically non-invertible gates arising from fusion rules within a unitary modular tensor category. Consequently, circuit optimization shifts from continuous geodesic paths to a discrete shortest-path problem on the graph of superselection sectors, offering a novel geometric cost function. By linking fusion transitions to boundary stress-tensor data, can this approach illuminate the emergence of shock-like defects and provide new insights into the AdS/CFT correspondence?

Beyond Simple Counts: A Geometric Approach to Quantum Complexity

Computational complexity, at its core, seeks to define the resources – time, energy, or material – required to achieve a specific task. In the realm of quantum computation, this translates to determining the ‘cost’ of creating a particular quantum state. Traditionally, Nielsen Complexity has served as a primary metric for this cost, essentially quantifying the minimal number of elementary quantum gates needed to build a desired state from a simple initial state. This measure is predicated on the idea that more complex states, requiring intricate sequences of operations, are inherently ‘more costly’ to prepare. Understanding this cost is not merely an academic exercise; it directly informs the feasibility of quantum algorithms and the limitations of quantum computers, as the complexity of state preparation often dictates the overall computational burden. $N_{abc}^{k}$ values play a role in assessing this complexity.

Traditional methods for quantifying quantum computational complexity, such as those based on gate counts or circuit depth, frequently encounter limitations when dealing with systems exhibiting conformal symmetry or undergoing non-unitary transformations. These standard measures often treat all operational steps as equally costly, failing to recognize that conformal transformations-preserving angles and shapes-can drastically alter the required resources, and that non-unitary operations, which don’t conserve probability, introduce fundamentally different computational challenges. Consequently, a simple tally of operations can significantly misrepresent the true ‘cost’ of preparing a particular quantum state within such systems; nuances inherent to these symmetries and transformations are lost, leading to inaccurate assessments of computational difficulty and potentially obscuring the underlying physics of the process.

Refining the quantification of quantum state preparation necessitates moving beyond traditional computational complexity measures, and a geometric approach provides a robust alternative. This framework utilizes the Kirillov Geometric Action and the Alekseev-Shatashvili Action to analyze the ‘cost’ associated with creating specific quantum states, particularly when dealing with systems exhibiting conformal symmetries or undergoing non-unitary transformations. The complexity of this calculation is fundamentally linked to fusion multiplicities, denoted as $N_{abc}^{k}$ , which represent the number of admissible outcomes when combining different quantum states. A higher number of possible fusion outcomes directly increases the computational burden, highlighting the crucial role of these geometric actions in accurately assessing and potentially minimizing the resources needed to prepare complex quantum states; by providing a more nuanced understanding of state preparation costs, these actions are essential for advancing quantum computation and information theory.

State evolution, represented by the dark line, is determined by sequences of gates (gray lines) that can produce multiple outcomes due to non-invertible actions, allowing for the construction of two distinct paths between initial and target states, as illustrated by the mirrored circuit processes.

Virasoro Circuits: Expanding Computational Horizons Beyond Unitary Evolution

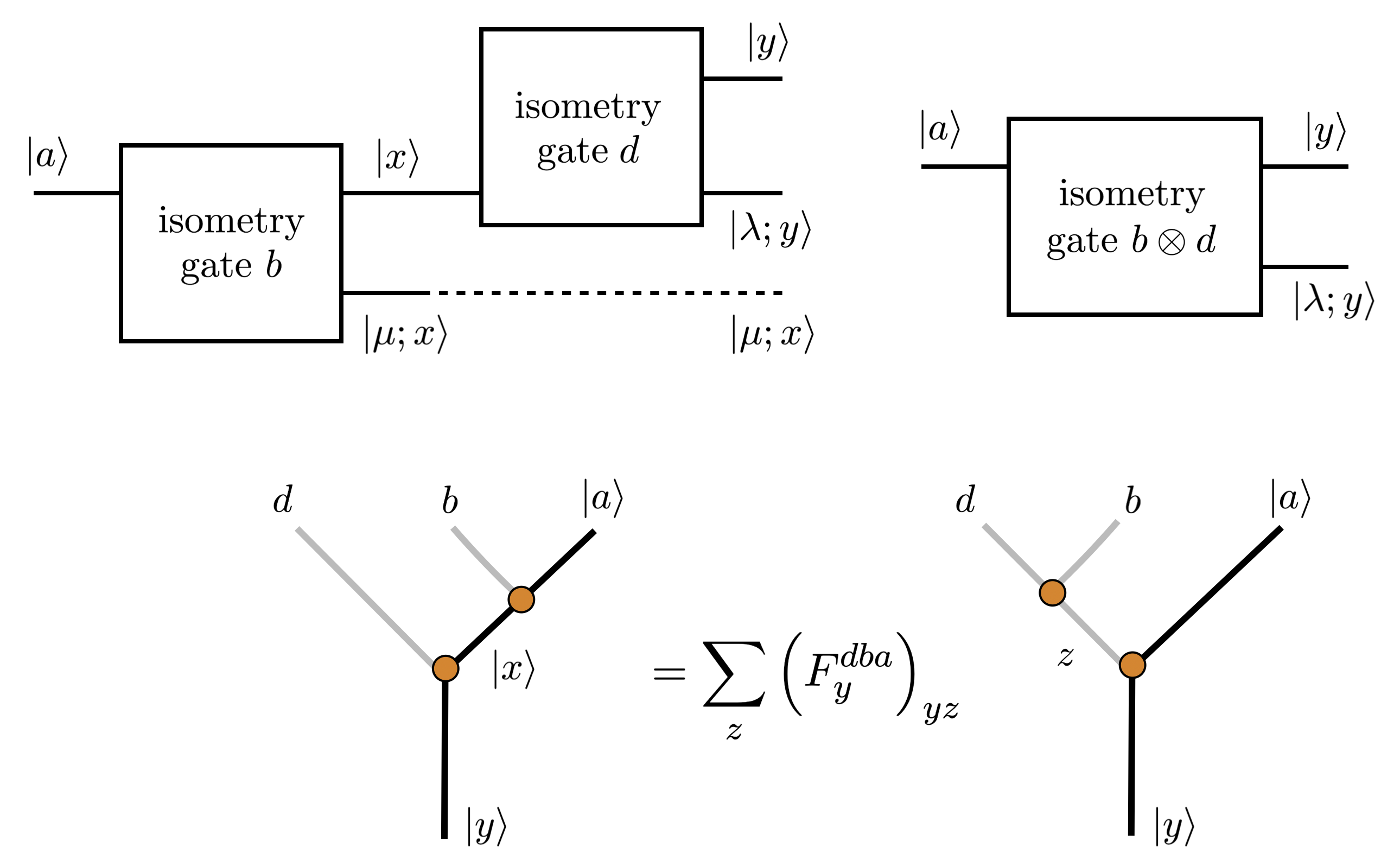
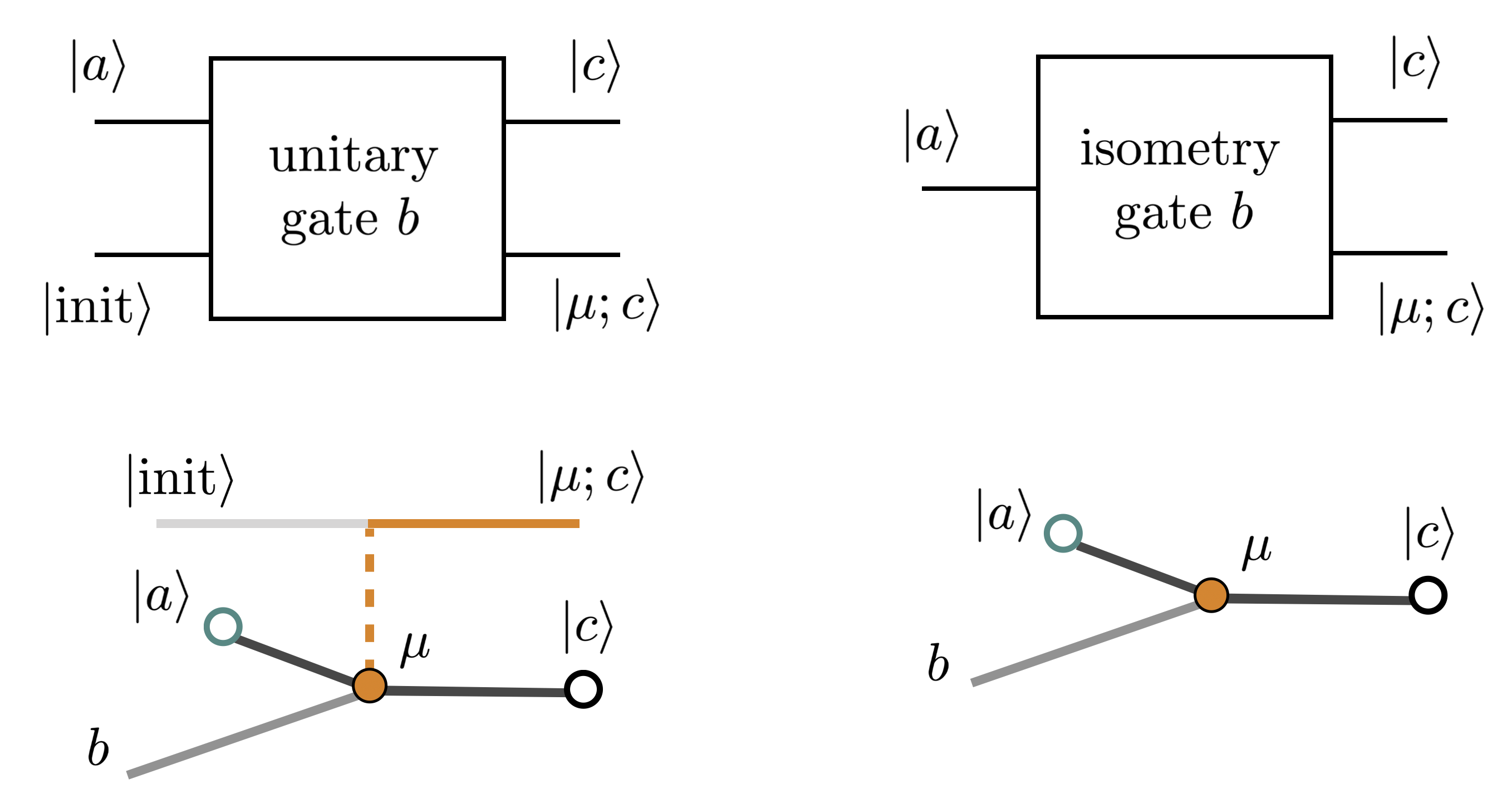
Virasoro circuits represent a distinct approach to quantum computation by leveraging the mathematical framework of Virasoro algebra to define the constituent gates. These circuits are not built on traditional qubit manipulations, but instead utilize gates derived from the infinite-dimensional symmetry group associated with two-dimensional conformal field theory. Specifically, Unitary Virasoro Gates – operators satisfying the constraints of unitary evolution – form the basis of computation within this architecture. The construction of these gates relies on representations of the Virasoro algebra, allowing for the implementation of quantum algorithms through a novel gate set distinct from standard Clifford or Toffoli gates. This approach allows for potentially more efficient representations of certain quantum operations and offers a new pathway toward exploring quantum computational models.

Virasoro circuits differentiate themselves from conventional quantum computation by incorporating non-invertible gates alongside unitary transformations. This inclusion allows for computations that exceed the representational capacity defined by standard Nielsen complexity, a metric based solely on reversible operations. Non-invertible gates introduce a controlled loss of information, which, within the framework of Virasoro algebras, is directly linked to the exploration of conformal symmetry. Specifically, the branching rules governing the composition of these gates, dictated by the underlying fusion rules, enable the systematic investigation of how conformal transformations affect quantum states and operators, potentially offering new avenues for quantum algorithms and simulations.

Virasoro circuit gate composition is governed by fusion rules which define the resultant state when combining operators; these rules are central to the circuits’ non-unitary character. Specifically, the fusion of two operators does not necessarily yield a single, deterministic outcome, but instead can branch into multiple possible states, each associated with a specific multiplicity determined by the branching rules. The complexity of the resulting system is directly proportional to the number of these branching outcomes and the associated multiplicities, as each branch represents a distinct computational path that must be accounted for during circuit evaluation. $\mathcal{F}(\alpha, \beta) = \sum_{\gamma} N_{\alpha \beta}^{\gamma} \gamma$ , where $N_{\alpha \beta}^{\gamma}$ denotes the multiplicity of operator γ in the fusion of operators α and β.

A fusion gate acts on a Virasoro representation <span class="katex-eq" data-katex-display="false">a</span>, mapping it to admissible output families <span class="katex-eq" data-katex-display="false">c</span> through fusion channels <span class="katex-eq" data-katex-display="false">\mu \in V^{c}_{ab}</span> which encode fusion data and are retained as auxiliary degrees of freedom in the Stinespring construction, where vertical columns represent full Virasoro modules. — A fusion gate acts on a Virasoro representation $a$ , mapping it to admissible output families $c$ through fusion channels $\mu \in V^{c}_{ab}$ which encode fusion data and are retained as auxiliary degrees of freedom in the Stinespring construction, where vertical columns represent full Virasoro modules.

A Formal Foundation: Tensor Categories and Rational Conformal Field Theory

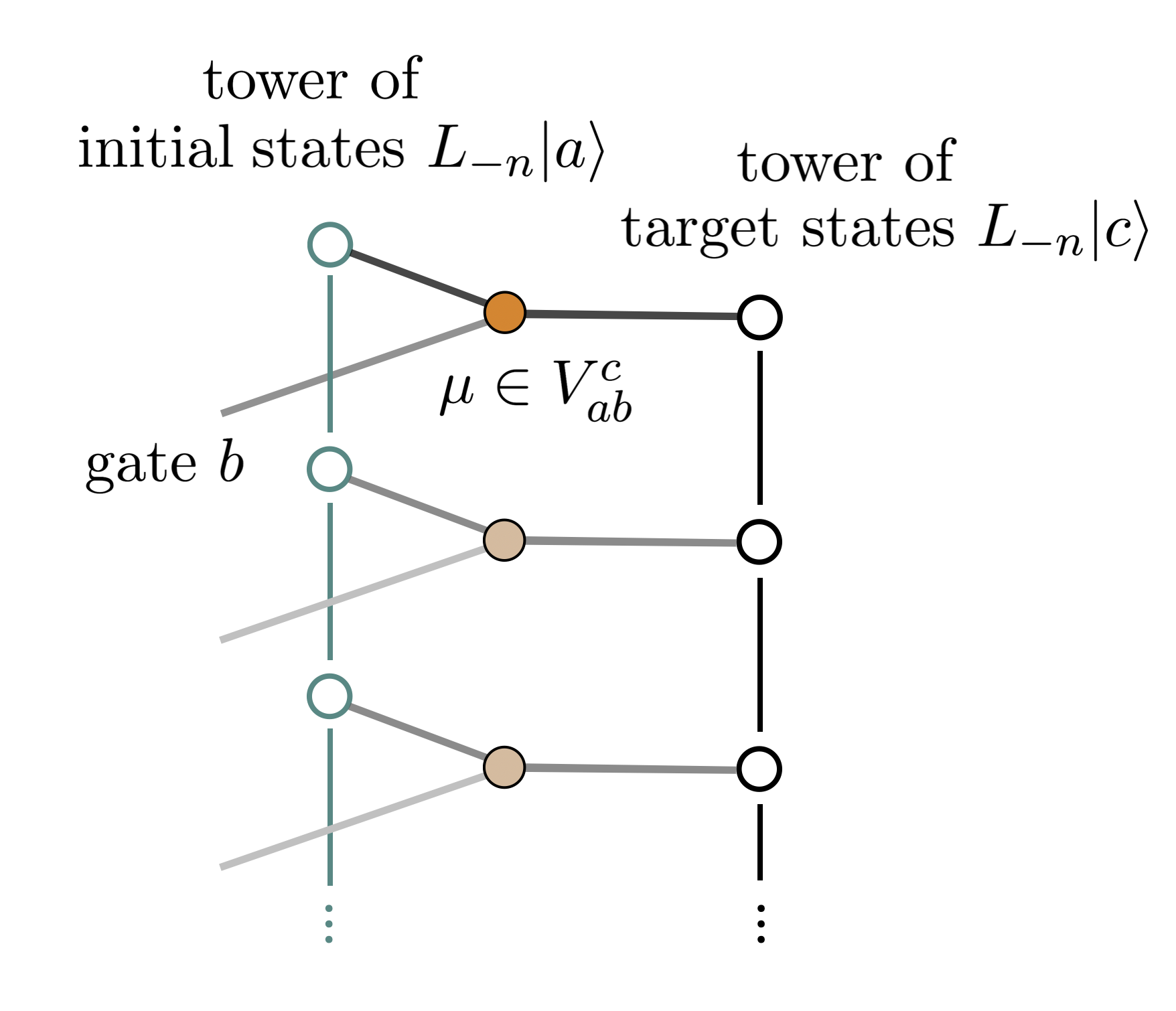
Unitary Modular Tensor Categories (UMTCs) provide a mathematical framework for precisely defining the behavior of non-invertible gates in quantum circuits. These categories are algebraic structures equipped with composition laws, braiding, and duality properties, allowing for a rigorous treatment of gate fusion. Specifically, the fusion rules within a UMTC dictate how the application of sequential non-invertible gates can be represented as a combination of simpler operations. The ‘unitary’ condition ensures probabilistic interpretations are preserved, while ‘modular’ properties relate the category’s structure to geometric transformations, enabling analysis of circuit connectivity and topological properties. The mathematical properties of the UMTC directly constrain the possible behaviors of the corresponding gates, enabling a complete and consistent description of their effects on quantum states, and providing tools to analyze and predict the outcomes of circuits built from these gates.

Rational Conformal Field Theory (RCFT) is a specific class of conformal field theory characterized by a finite number of primary fields, also known as irreducible representations of the conformal symmetry group. This finiteness is crucial as it leads to a modular bootstrap, allowing for the complete determination of the theory from a small set of data. The connection to tensor categories arises because the fusion rules of the primary fields in RCFT directly correspond to the tensor product and decomposition rules within the associated tensor category. Specifically, the braiding and fusion properties of objects in the tensor category mirror the exchange and composition of primary fields in the RCFT, enabling a rigorous mathematical framework for analyzing and classifying these theories and their associated algebras; the category completely reconstructs the RCFT and vice-versa.

The dynamics of circuits employing non-invertible gates are demonstrably linked to the symmetries inherent in two-dimensional conformal field theories (CFTs). This correspondence arises because the fusion rules governing the behavior of these gates are formally equivalent to the operator product expansion (OPE) coefficients within a Rational CFT. Specifically, the Energy Shift $E_c$ -a parameter characterizing the non-invertible gates-directly impacts the computational cost associated with simulating the circuit; larger $E_c$ values generally correlate with increased circuit complexity and resource requirements. The structure of the tensor category defining the gate set constrains the possible CFTs, effectively mapping circuit properties to features of the corresponding conformal field theory.

Isometric gates, achieved through fusion, expand the Hilbert space with junction degrees of freedom that function as ancillas within the Stinespring representation, contrasting with the operation of unitary gates.

Geometric Echoes: Spacetime, Bañados Geometry, and Defect Structures

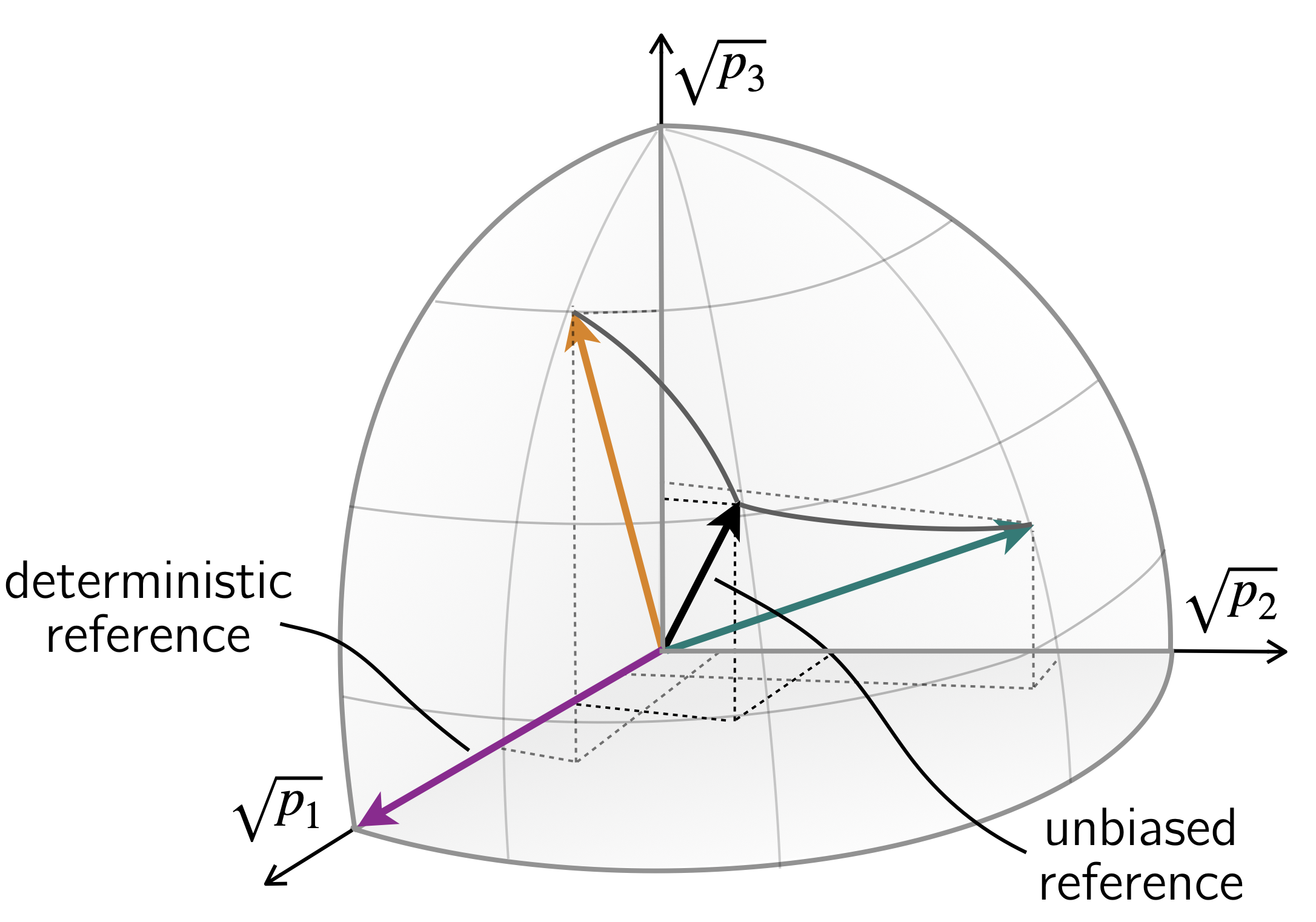
The intricate design of these quantum circuits isn’t merely abstract; it’s deeply interwoven with the fabric of spacetime, specifically through a connection to Bañados geometry. This three-dimensional spacetime is particularly significant in the realm of holographic duality, a theoretical framework positing a correspondence between gravity in a higher-dimensional space and a quantum field theory in a lower-dimensional one-in this case, a two-dimensional Conformal Field Theory (CFT). The geometry arises as a solution to Einstein’s equations with a negative cosmological constant, creating a spacetime with unique properties. Establishing this link suggests the circuits aren’t just modeling aspects of quantum gravity, but are geometrically realized within a spacetime that shares characteristics with those explored in advanced theoretical physics. The correspondence allows researchers to investigate complex gravitational phenomena through the more tractable lens of quantum field theory, and vice-versa, potentially providing new avenues for understanding the fundamental nature of spacetime itself.

Within the geometric framework established by these circuits, calculations reveal that abrupt changes, or discontinuities, emerge in the boundary stress-tensor – a measure of energy and momentum flow at the circuit’s edge. These aren’t merely mathematical artifacts, but manifest as what are termed ‘Shock-like Defects’ – localized disruptions in the otherwise smooth distribution of energy. Crucially, these defects aren’t imposed as external conditions, but arise naturally from the underlying geometry. The appearance of these shock-like features suggests that the circuit’s structure isn’t simply analogous to spacetime, but actively embodies aspects of its dynamics, potentially offering a tangible way to model and explore phenomena like black holes or cosmological phase transitions, all through the lens of circuit behavior. The energy density is described by $\sigma = \frac{T}{\epsilon}$ , and the shock defects occur when this density becomes discontinuous.

The surprising correspondence between the architecture of these quantum circuits and the geometry of spacetime hints at a profoundly interconnected reality, potentially offering a novel pathway toward resolving the long-standing puzzle of quantum gravity. Researchers posit that the circuit’s structure isn’t merely analogous to spacetime geometry-specifically, the Bañados metric-but fundamentally reflects it, suggesting that quantum information processing may be intrinsically linked to the curvature and topology of the universe. This connection implies that understanding the behavior of quantum systems, and manipulating their information flow, could yield insights into the very fabric of spacetime, and vice versa. Furthermore, the emergence of Shock-like defects within the circuits, corresponding to discontinuities in the boundary stress-tensor, provides a concrete, testable bridge between abstract mathematical constructs and physical phenomena, opening exciting possibilities for exploring gravitational effects through controlled quantum experiments and potentially formulating a more complete theory uniting quantum mechanics and general relativity.

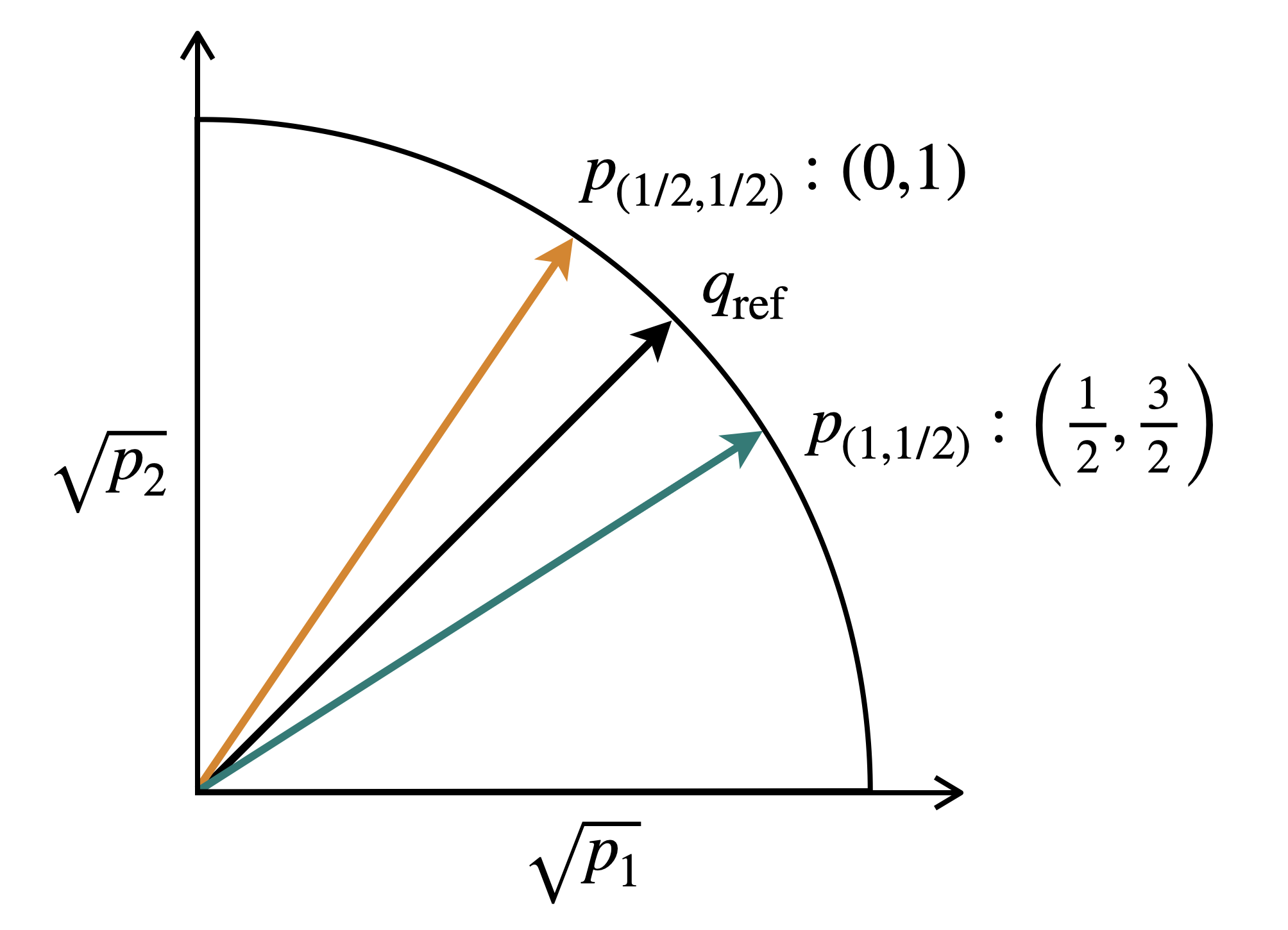
The <span class="katex-eq" data-katex-display="false">su(2)^4\widehat{su(2)}\_{4}</span> fusion graph demonstrates multiple paths between spin labels, with solid arrows representing <span class="katex-eq" data-katex-display="false">b=\tfrac{1}{2}</span> fusion steps and dashed arrows indicating unselected options, while the corresponding weight vectors for two-channel fusion lie on a unit quarter-circle, indicating intrinsic gate costs and varying degrees of determinism in channel selection. — The $su(2)^4\widehat{su(2)}\_{4}$ fusion graph demonstrates multiple paths between spin labels, with solid arrows representing $b=\tfrac{1}{2}$ fusion steps and dashed arrows indicating unselected options, while the corresponding weight vectors for two-channel fusion lie on a unit quarter-circle, indicating intrinsic gate costs and varying degrees of determinism in channel selection.

Beyond Gate Counts: Refining the Measure of Quantum Computational Cost

Traditional metrics for quantifying the ‘cost’ of quantum gate operations often fall short by neglecting crucial geometric information embedded within the quantum circuit’s parameter space. Recent advancements propose an ‘Energy-Weighted Cost’ that refines these calculations by incorporating both conformal weight shifts and bulk holonomy data – essentially, how much ‘effort’ is required to navigate the circuit’s landscape. This approach moves beyond simple gate counts, instead focusing on the energetic cost of transitioning between different quantum states during computation. By accounting for these subtle shifts and holonomies, the Energy-Weighted Cost offers a more accurate and nuanced assessment of circuit complexity, potentially enabling the optimization of quantum algorithms and a better understanding of their fundamental limitations. $\text{Cost} = \in t \sqrt{g_{ij} dx^i dx^j}$ represents a simplified view of this energetic cost calculation, where $g_{ij}$ embodies the metric tensor derived from conformal and holonomic data.

A robust quantification of circuit cost necessitates a distance metric unaffected by arbitrary choices in how quantum states are represented. The Fubini-Study metric fulfills this requirement, offering a basis-independent means of measuring the dissimilarity between quantum states – essentially, the minimal ‘effort’ required to transform one state into another. This metric isn’t simply a mathematical tool; it underpins the calculation of ‘Selection Cost’, a component of refined gate cost analysis. By quantifying the distance between the weight vectors representing different fusion channels within a quantum circuit, the Fubini-Study metric allows researchers to accurately assess the complexity associated with selecting a particular outcome from multiple possibilities, even in circuits that aren’t strictly unitary. This approach moves beyond traditional cost calculations, providing a more nuanced and reliable measure of computational effort directly proportional to the Fubini-Study Distance.

The conventional assessment of circuit cost often overlooks the energetic implications of choosing a single outcome when multiple quantum fusion channels are available. This ‘Selection Cost’ represents the energy dissipated when a specific result is favored, extending the applicability of cost calculations to non-unitary circuits-systems where information isn’t strictly conserved. Researchers quantify this cost using the Fubini-Study metric, a basis-independent measure of distance, to determine the separation between the weight vectors representing each fusion channel’s probability. Consequently, a circuit’s complexity is no longer simply a count of gates, but a quantifiable distance-directly proportional to this Fubini-Study distance-reflecting the energetic cost of selecting a specific computational path and offering a more nuanced understanding of quantum circuit efficiency.

The intrinsic cost of a fusion process, represented by arc length, depends on the normalized weight vectors <span class="katex-eq" data-katex-display="false">\sqrt{p_1}, \sqrt{p_2}, \sqrt{p_3}</span> across three channels, ranging from a uniform distribution (black) to a deterministic selection (purple) and exemplified by two non-uniform outcomes (green and orange). — The intrinsic cost of a fusion process, represented by arc length, depends on the normalized weight vectors $\sqrt{p_1}, \sqrt{p_2}, \sqrt{p_3}$ across three channels, ranging from a uniform distribution (black) to a deterministic selection (purple) and exemplified by two non-uniform outcomes (green and orange).

The exploration of non-invertible symmetries within quantum circuits, as detailed in the article, echoes a deeper concern: the encoding of worldview within systems. Any framework prioritizing computational efficiency at the expense of acknowledging symmetry’s limitations carries an inherent ethical cost. As Jürgen Habermas observed, “The claim to validity of a statement is raised in the first instance when it is brought forward.” This principle applies directly to the geometric cost function proposed; its validity isn’t merely mathematical, but rests on a responsible accounting for the symmetries – and their potential inversions – it chooses to represent. Ignoring these nuances isn’t just a technical oversight; it’s a decision that shapes the very foundations of the AdS/CFT correspondence and, potentially, our understanding of gravity itself.

What Lies Ahead?

The extension of circuit complexity to encompass non-invertible symmetries is not merely a technical refinement, but a necessary confrontation with the limitations of unitarity as a foundational principle. The framework presented here reveals that geometric cost functions, when built upon non-invertible operations, inherently encode assumptions about information loss-or, more precisely, about what constitutes ‘information’ in the first place. To pursue this further demands a careful examination of the precise relationship between fusion rules and emergent spacetime geometry; scalability without a robust understanding of these rules risks acceleration toward formal elegance divorced from physical meaning.

A crucial challenge lies in translating these theoretical circuits into concrete gravitational observables. The AdS/CFT correspondence, while providing a powerful dictionary, remains largely phenomenological. Future work must focus on identifying specific gravitational signatures-deviations from classical behavior, perhaps-that betray the presence of non-invertible symmetries in the boundary conformal field theory. This will require moving beyond perturbative analyses and confronting the inherently non-local nature of these symmetries.

Ultimately, this line of inquiry compels a reassessment of the very notion of ‘complexity’ itself. If information can be genuinely lost, or transformed in ways that defy conventional description, then the standard metrics used to quantify complexity become inadequate. The field must embrace a more nuanced perspective, one where privacy is not a checkbox to be ticked, but a design principle woven into the fabric of the computational model.

Original article: https://arxiv.org/pdf/2601.09534.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/