Bridging the Gaps: Learning from Incomplete and Diverse Data

by

Author: Denis Avetisyan

A new framework addresses the challenges of integrating multi-modal datasets when information is missing or varies significantly between sources.

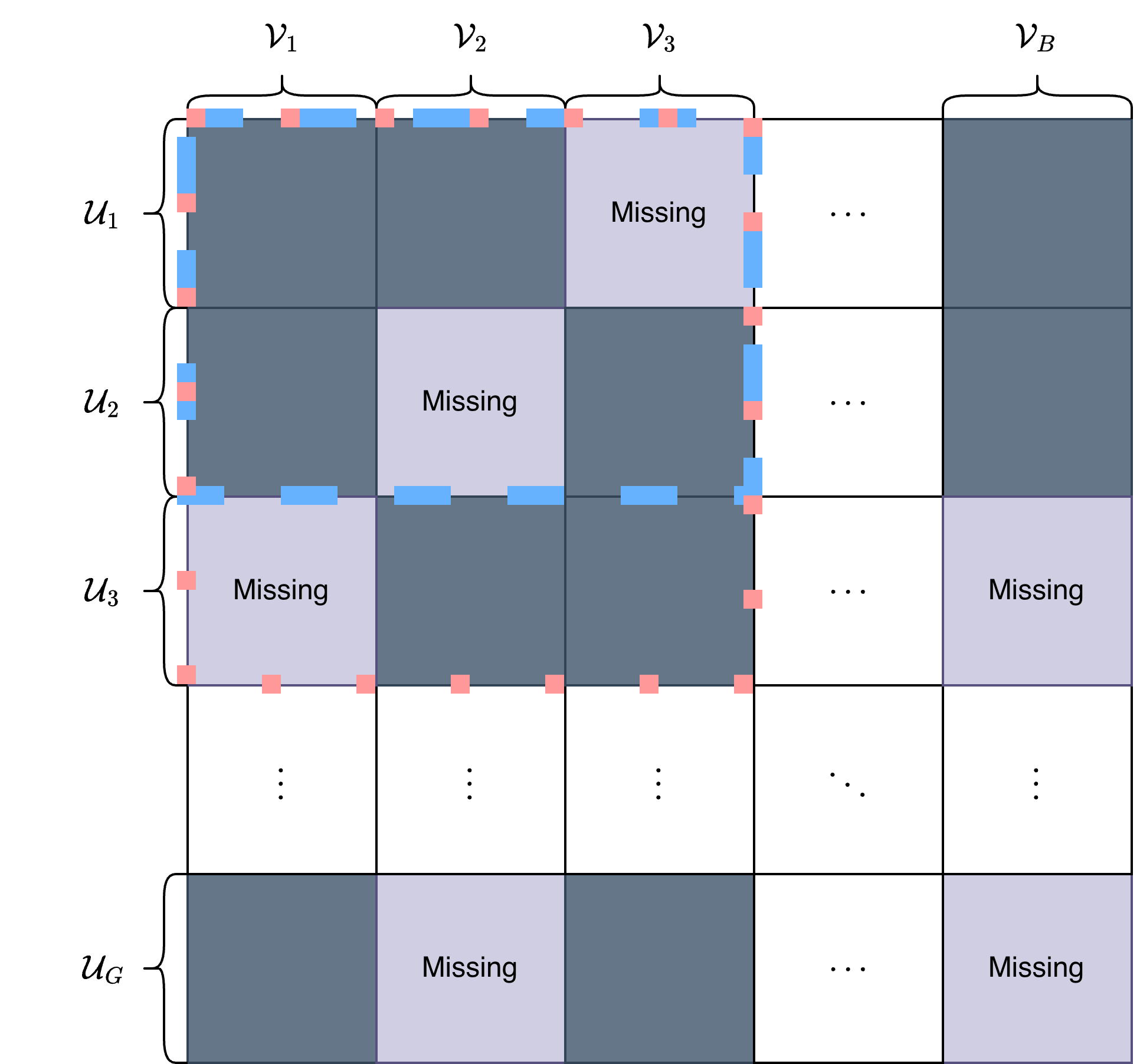
The study investigates missing data patterns across subject groups and feature blocks, focusing on two configurations-a <span class="katex-eq" data-katex-display="false">2 \times 32 \times 3</span> scenario and a <span class="katex-eq" data-katex-display="false">3 \times 33 \times 3</span> configuration-to assess the robustness of analytical methods when faced with incomplete datasets.
The study investigates missing data patterns across subject groups and feature blocks, focusing on two configurations-a 2 \times 32 \times 3 scenario and a 3 \times 33 \times 3 configuration-to assess the robustness of analytical methods when faced with incomplete datasets.

This paper introduces Anchor Projected Principal Component Analysis (APPCA) for robust representation learning in the presence of blockwise missingness and signal heterogeneity.

Integrating multi-source data is often hindered by the practical challenges of incomplete observations and varying signal strengths across different feature sets. This paper, ‘Representation Learning with Blockwise Missingness and Signal Heterogeneity’, introduces Anchor Projected Principal Component Analysis (APPCA), a novel framework designed to address these issues in representation learning. By prioritizing robust subspace recovery and projecting data onto low-dimensional “anchor” spaces, APPCA achieves accurate data integration even with significant missingness and heterogeneous signal strengths, demonstrated through theoretical error bounds and empirical validation. Could this approach unlock more effective methods for analyzing complex, multi-modal datasets in fields like genomics and beyond?

The Illusion of Integration: Why Single-Cell Data Still Bites Back

The advent of single-cell multi-omics technologies, such as TEA-seq, promises an unprecedented resolution into the complexities of cellular states, enabling researchers to characterize cells based on multiple layers of biological information simultaneously. However, realizing this potential is significantly challenged by the inherent difficulties in integrating these diverse datasets. Unlike traditional single-cell analyses focusing on a single modality – like gene expression – multi-omics data combines information from genomics, transcriptomics, proteomics, and more. This integration isn’t simply a matter of combining tables; it requires sophisticated computational approaches to reconcile different data types, account for varying levels of noise, and address technical biases introduced during sample preparation and data acquisition. The resulting datasets, while incredibly rich, present a formidable analytical hurdle, demanding novel strategies to extract meaningful biological insights and avoid spurious correlations.

The integration of data from single-cell multi-omics experiments is frequently complicated by a phenomenon known as blockwise missingness. This occurs when entire groups, or ‘blocks,’ of features – representing specific omics measurements like gene expression or protein abundance – are systematically absent for a subset of cells. Unlike random data loss, blockwise missingness isn’t simply a matter of technical failure in detecting a signal; it arises inherently from the experimental design or the nature of the biological system under study. For example, certain assays might not be applicable to all cell types, or a technical limitation might prevent the measurement of a particular omics layer in a fraction of cells. This patterned absence of data introduces significant biases if not properly addressed, potentially leading to inaccurate cell type identification, distorted trajectory inference, and flawed interpretations of cellular heterogeneity. Consequently, effective computational strategies are crucial for imputing missing values or accommodating blockwise missingness during data analysis to ensure robust and reliable results.

Signal heterogeneity within single-cell multi-omics data presents a significant impediment to accurate data integration. This phenomenon, characterized by inconsistent signal strengths across different feature blocks – such as gene expression, protein levels, or chromatin accessibility – and varying between cell groups, introduces substantial noise and bias. Variations in assay sensitivity, differing cellular processes affecting signal generation, and technical factors all contribute to this inconsistency. Consequently, standard integration methods can disproportionately weight certain features or cell populations, masking true biological signals and leading to skewed interpretations of cellular states. Addressing signal heterogeneity is therefore crucial for constructing a comprehensive and reliable picture of cellular complexity from these increasingly prevalent datasets, demanding sophisticated analytical approaches capable of normalizing for these inherent biases.

APPCA: A Framework for Wrangling the Chaos

Anchor Projected Principal Component Analysis (APPCA) is a representation learning framework developed to address challenges inherent in integrating multi-omic datasets. Specifically, APPCA is designed to handle scenarios with blockwise missingness – where entire blocks of features are absent – and signal heterogeneity, referring to differing underlying structures across data sources. The framework achieves integration by learning a low-dimensional representation that accounts for these issues, enabling downstream analyses to be performed on a unified dataset. This is accomplished through a process of projecting data onto shared, or ‘anchor’, features, effectively reducing noise and improving the accuracy of multi-omic data integration compared to methods that do not explicitly account for missing data patterns or differing underlying signals.

Anchor projection, a core component of APPCA, enhances multi-omics data integration by identifying and prioritizing shared features – termed ‘anchors’ – across different data blocks. This process effectively reduces noise by focusing the integration procedure on these common elements, rather than attempting to align disparate, individual features. The technique projects each data block onto a lower-dimensional subspace defined by the selected anchors, minimizing the impact of block-specific noise and maximizing the signal derived from the shared biological processes represented by these features. By concentrating on these anchors, APPCA improves the robustness and accuracy of downstream analyses, such as identifying differentially expressed genes or predicting clinical outcomes, even in the presence of substantial missing data.

Groupwise subspace recovery within the APPCA framework operates by identifying and reconstructing the low-dimensional subspace shared across different feature blocks, even when data is incomplete. This is achieved by treating each group of correlated features (e.g., genomics, proteomics, metabolomics) as a block and utilizing all available data within and across these blocks to estimate a common, underlying subspace. The method employs techniques to handle blockwise missingness, meaning that entire feature blocks may be absent for some samples, without requiring complete data across all features. By leveraging the relationships between features within each block and the shared structure across blocks, APPCA aims to improve the accuracy and robustness of multi-omics data integration and downstream analysis. The recovered subspace represents a compressed, noise-reduced representation of the original high-dimensional data, facilitating improved biological interpretation.

Beyond the Basics: Refining APPCA for Real-World Data

The Chain-Linked Extension augments APPCA’s capabilities by addressing complex blockwise missingness patterns through sequential merging of overlapping data groups. This process allows APPCA to effectively reconstruct data even when missing blocks are not fully disjoint, a limitation of standard blockwise imputation techniques. By iteratively combining these groups, the extension propagates information across partially observed blocks, improving the accuracy of data completion and subsequent analysis. The methodology differs from traditional approaches by not requiring pre-defined, non-overlapping blocks, and thereby offers a more flexible approach to handling diverse missing data structures.

APPCA incorporates Spectral Slicing to maintain reconstruction accuracy in challenging data conditions. This technique establishes error bounds for reconstruction that are demonstrably controlled, even when dealing with heterogeneous data or weak signals. Critically, these bounds are independent of the condition number of subject embeddings; a high condition number typically indicates instability and can lead to unreliable reconstructions. By decoupling error control from this potentially problematic metric, Spectral Slicing enhances APPCA’s robustness and ensures consistent performance across a wider range of datasets and signal strengths.

Evaluations on a single-cell multimodal dataset demonstrate APPCA’s reconstruction performance, achieving a normalized F-norm reconstruction error below 0.521. This result indicates that APPCA outperforms both Shared Block PCA and two-step embedding alignment methods in reconstructing the original data from its reduced representation. The normalized F-norm, a measure of the difference between the original and reconstructed data, provides a quantitative assessment of reconstruction accuracy, with lower values indicating better performance. This benchmark suggests APPCA effectively captures and preserves the underlying data structure during dimensionality reduction in multimodal single-cell data.

Evaluation on simulated datasets demonstrates APPCA’s superior performance in information aggregation, achieving error rates that scale with the oracle estimator at a rate of 1/\sqrt{p}, where p represents the number of features. This indicates that APPCA’s error diminishes proportionally to the inverse of the square root of the feature count, a characteristic of statistically efficient estimators. Comparative analysis reveals that baseline methods exhibit significantly higher error rates under identical simulation conditions, confirming APPCA’s enhanced ability to effectively utilize available data and minimize reconstruction error.

The Promise and Peril of Resolving Cellular Heterogeneity

APPCA establishes a powerful new approach to single-cell data integration, moving beyond limitations inherent in previous methods. By accurately aligning datasets generated from different technologies or experimental conditions, it reveals previously obscured connections within complex cellular populations. This framework doesn’t simply combine data; it reconstructs a cohesive representation of cellular states, allowing researchers to identify subtle variations and relationships that would otherwise remain hidden. Consequently, APPCA facilitates the discovery of novel cell types, developmental trajectories, and functional groupings, offering a more complete and nuanced understanding of cellular heterogeneity and its role in both health and disease.

A more complete integration of single-cell data, facilitated by advanced computational methods, is revealing previously obscured connections between a cell’s state – its functional characteristics at a given time – and its broader role within complex biological systems. This deepened understanding extends beyond simple categorization, allowing researchers to pinpoint subtle but critical differences in cellular behavior that contribute to disease development and progression. By accurately mapping these functional states, investigations can now identify potential therapeutic targets with greater precision, moving away from broad-spectrum treatments towards interventions tailored to specific cellular mechanisms. Consequently, this approach holds considerable promise for developing more effective therapies and ultimately, improving patient outcomes by addressing the root causes of disease at the single-cell level.

The advent of APPCA signifies a considerable leap towards resolving the intricacies of cellular heterogeneity, moving beyond broad classifications to reveal subtle distinctions within seemingly uniform cell populations. This enhanced resolution is not merely academic; it directly fuels the promise of personalized medicine by enabling the identification of patient-specific cellular profiles and responses. Consequently, therapeutic strategies can be tailored to address the unique characteristics of an individual’s disease, maximizing efficacy while minimizing adverse effects. Furthermore, APPCA facilitates the discovery of previously unrecognized therapeutic targets by pinpointing the specific cellular subtypes driving disease progression, ultimately fostering the development of more precise and effective interventions.

The pursuit of elegant frameworks, like the proposed Anchor Projected Principal Component Analysis, often feels like building sandcastles against the tide. This work attempts to address the inherent chaos of real-world data – blockwise missingness and signal heterogeneity – by projecting onto lower-dimensional spaces. It’s a valiant effort, but one keenly aware that production environments will inevitably find novel ways to introduce unforeseen complexities. As Leonardo da Vinci observed, “Simplicity is the ultimate sophistication.” The irony, of course, is that achieving true simplicity in data integration requires wrestling with increasingly intricate problems, knowing full well that today’s robust solution becomes tomorrow’s technical debt. The focus on subspace recovery is commendable, a necessary compromise in the face of incomplete and varied signals.

What’s Next?

The pursuit of robust multi-modal integration inevitably leads to ever more sophisticated methods for handling incomplete data. This work, with its focus on subspace recovery and anchor projections, feels less like a solution and more like a temporary stay of execution. The bug tracker, one anticipates, will fill with edge cases arising from signal heterogeneity not anticipated by current models. The assumption that a low-dimensional projection will consistently capture ‘global representations’ is a comforting narrative, but production systems rarely adhere to elegance.

The real challenge isn’t merely filling in missing data, but acknowledging that some data should remain missing. The framework skirts the issue of intentional data obfuscation-the deliberate introduction of noise to protect privacy or intellectual property. Future work will likely grapple with adversarial attacks specifically designed to exploit the reconstruction process, turning the ‘anchor’ into a liability. It isn’t about finding the perfect projection; it’s about building systems resilient enough to function when the projection inevitably fails.

The field will undoubtedly see more complex variations of this theme-more anchors, more projections, more assumptions about underlying structure. One suspects the ultimate outcome will be a library of specialized patches for specific data configurations. They don’t deploy – they let go.

Original article: https://arxiv.org/pdf/2602.11511.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

See also:

2026-02-14 22:06