Building Brain-Inspired Resilience: Error Correction for Neural Networks

Author: Denis Avetisyan

A new coding framework enhances the robustness of neural networks against errors in both memory and computation, mimicking the brain’s inherent fault tolerance.

Error correction within an ECC-DNN demonstrably improves MNIST test classification accuracy as the number of weight errors increases, highlighting the system’s resilience to data corruption and suggesting a robust approach to maintaining performance in noisy environments.

This work introduces real-valued linear constraints within neural network weights to enable the detection and correction of errors without increasing model complexity.

Despite increasing reliance on neural networks in critical applications, their vulnerability to both memory faults and computational errors remains a significant limitation. The paper, ‘Repair Brain Damage: Real-Numbered Error Correction Code for Neural Network’, addresses this challenge by introducing a novel error correction coding framework. This approach leverages real-valued linear constraints on network weights to detect and correct errors without increasing model complexity or sacrificing classification performance. Could this technique pave the way for truly robust and reliable artificial intelligence systems?

The Fragility of Deep Networks: A Systemic Vulnerability

Despite their demonstrated capabilities in complex tasks, deep neural networks exhibit a surprising fragility when confronted with even minor computational or memory errors. The very architecture that allows these networks to learn intricate patterns also creates vulnerabilities; a single bit flip, a transient power fluctuation, or a minor data corruption during memory access can propagate through layers, leading to significant performance degradation or even complete failure. This susceptibility isn’t merely theoretical – real-world deployments are increasingly susceptible to such errors given the growing complexity of networks and the resource constraints of edge devices. The issue stems from the network’s reliance on precise numerical calculations and the accumulation of rounding errors; a small deviation at one point can be amplified as data flows through numerous interconnected layers, highlighting a critical gap between theoretical power and practical reliability.

The seemingly robust performance of deep neural networks often belies a surprising fragility; even minor computational or memory errors can precipitate substantial declines in accuracy and reliability. This vulnerability stems from the complex interplay of numerous parameters, where a single, subtle corruption can propagate through the network, disrupting carefully learned representations. The implications are particularly concerning in critical applications such as autonomous vehicles, medical diagnostics, and financial modeling, where even a small error rate can have significant, even catastrophic, consequences. While networks can demonstrate high average performance, this metric often obscures the potential for unpredictable failures stemming from these often-overlooked parameter sensitivities, demanding a greater focus on robustness and error resilience in network design and deployment.

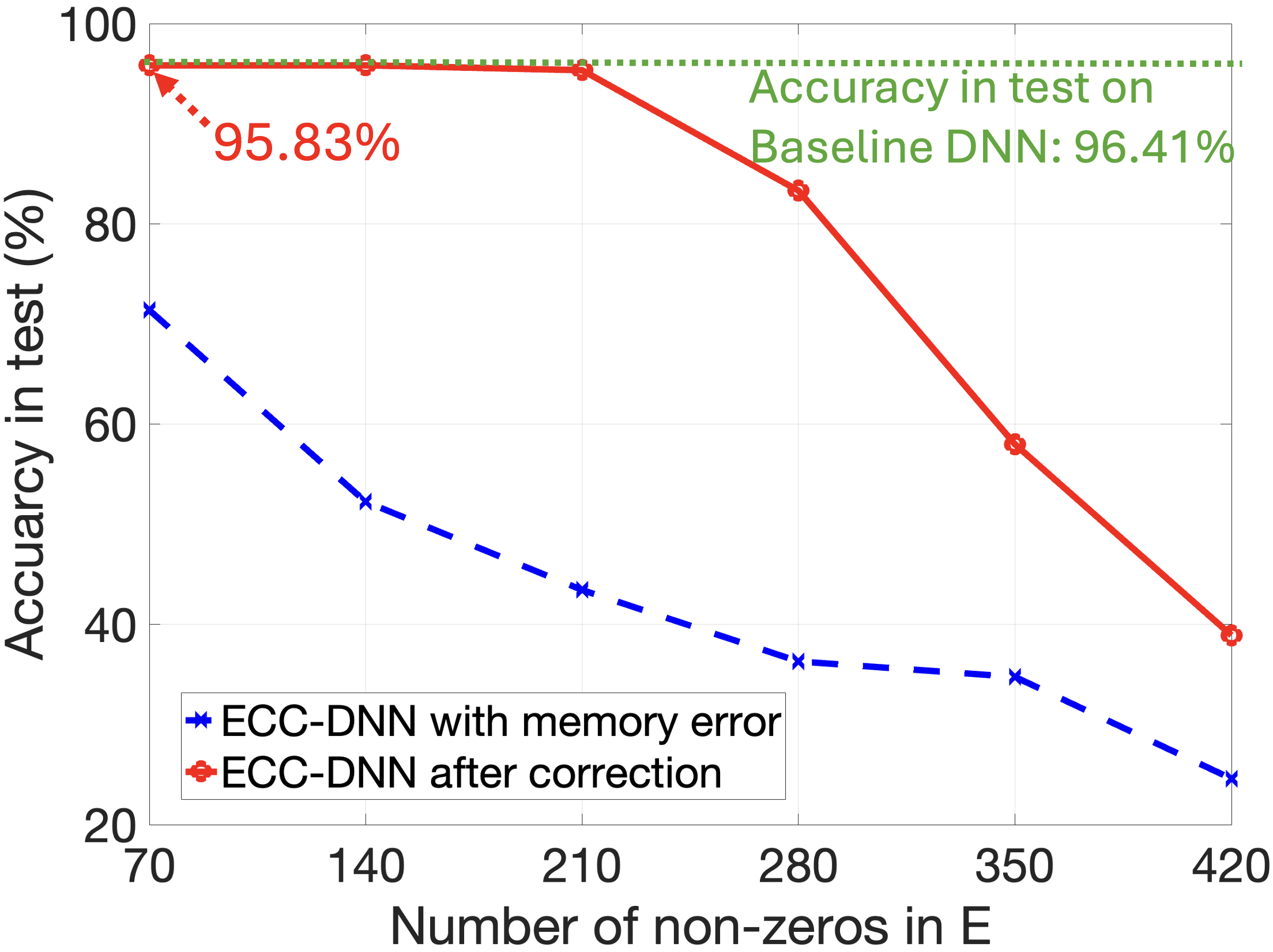
Current approaches to deep neural network design frequently prioritize accuracy without adequately assessing resilience to inevitable computational errors. Research indicates that even a substantial number of parameter corruptions – up to 210 errors within a 5120-parameter output layer – may go unnoticed during standard training and validation procedures. This oversight poses a significant risk, as seemingly minor distortions can accumulate and propagate through the network, leading to unpredictable and potentially catastrophic failures in real-world applications. The inherent fragility suggests a need for novel training methodologies and error-detection mechanisms that specifically target parameter robustness, moving beyond a sole focus on achieving peak performance on clean datasets.

Error correction significantly improves the test classification accuracy of ECC-DNNs on the CIFAR-10 dataset.

Error Correction as a Foundational Principle for Network Resilience

Real-Numbered Error Correction Codes represent a novel technique for enhancing the reliability of Deep Neural Networks by directly addressing the impact of errors during computation. Unlike traditional error correction methods designed for discrete data, these codes operate on the continuous values of network parameters and activations. This allows for the detection and correction of errors introduced by hardware faults, numerical instability, or adversarial attacks. The core principle involves encoding redundant information within the network’s weights and biases, enabling the reconstruction of correct values even when some parameters are corrupted. This approach differs from retraining or regularization techniques by providing a guaranteed level of robustness against a defined number of errors, independent of the training data or optimization process.

Encoding robustness directly into network parameters involves modifying the weights and biases of a Deep Neural Network to incorporate error-correcting properties. This is achieved by representing each parameter as a code word, allowing the network to tolerate deviations from its nominal values caused by computational errors-such as those arising from hardware imperfections-or memory faults. The redundancy inherent in the encoded parameters enables the reconstruction of the original, intended value even if a subset of bits is corrupted, thereby maintaining network functionality and preventing catastrophic failures. This approach differs from traditional fault tolerance methods which often involve redundant hardware or software components, instead focusing on intrinsic resilience within the model itself.

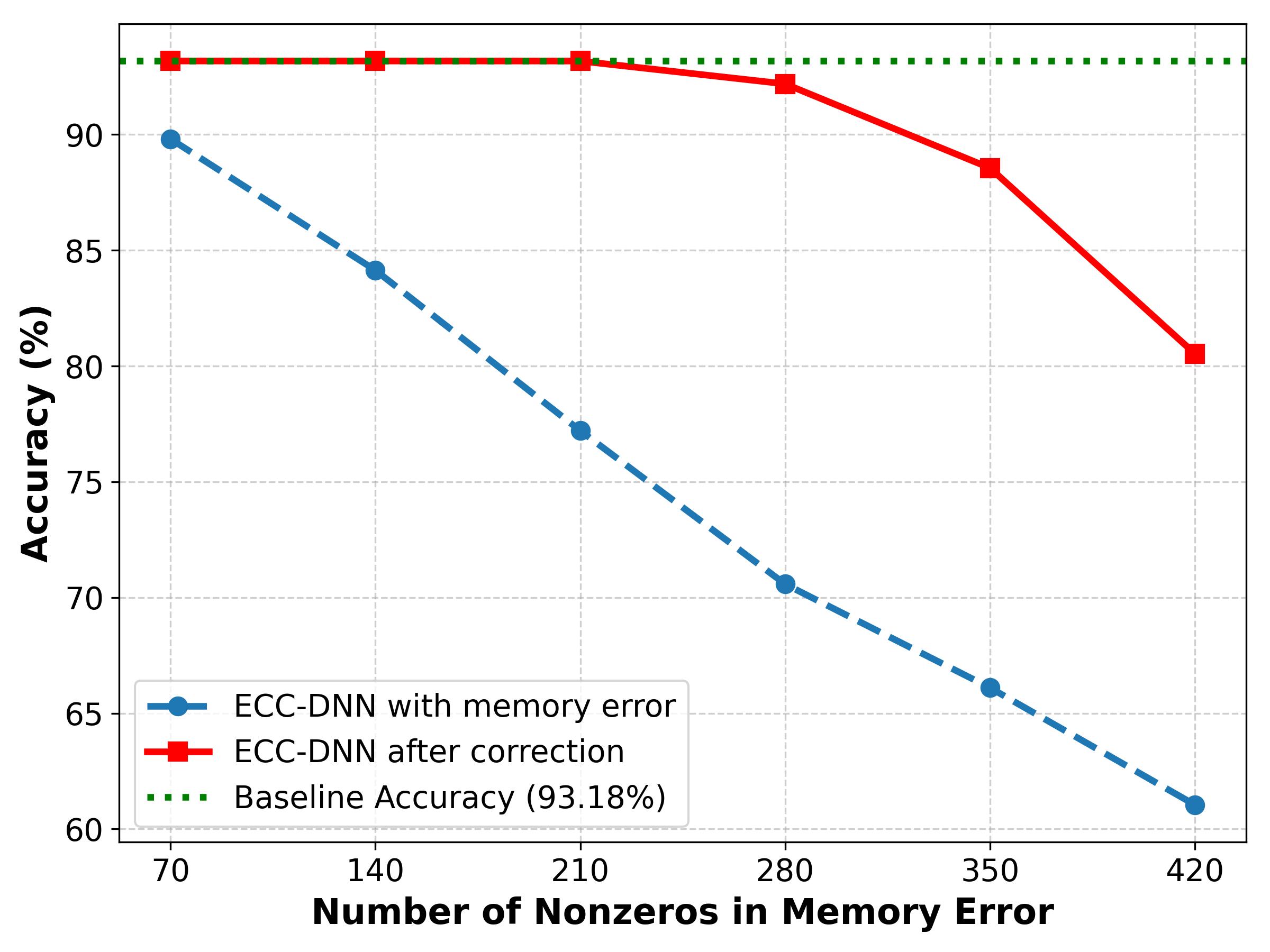
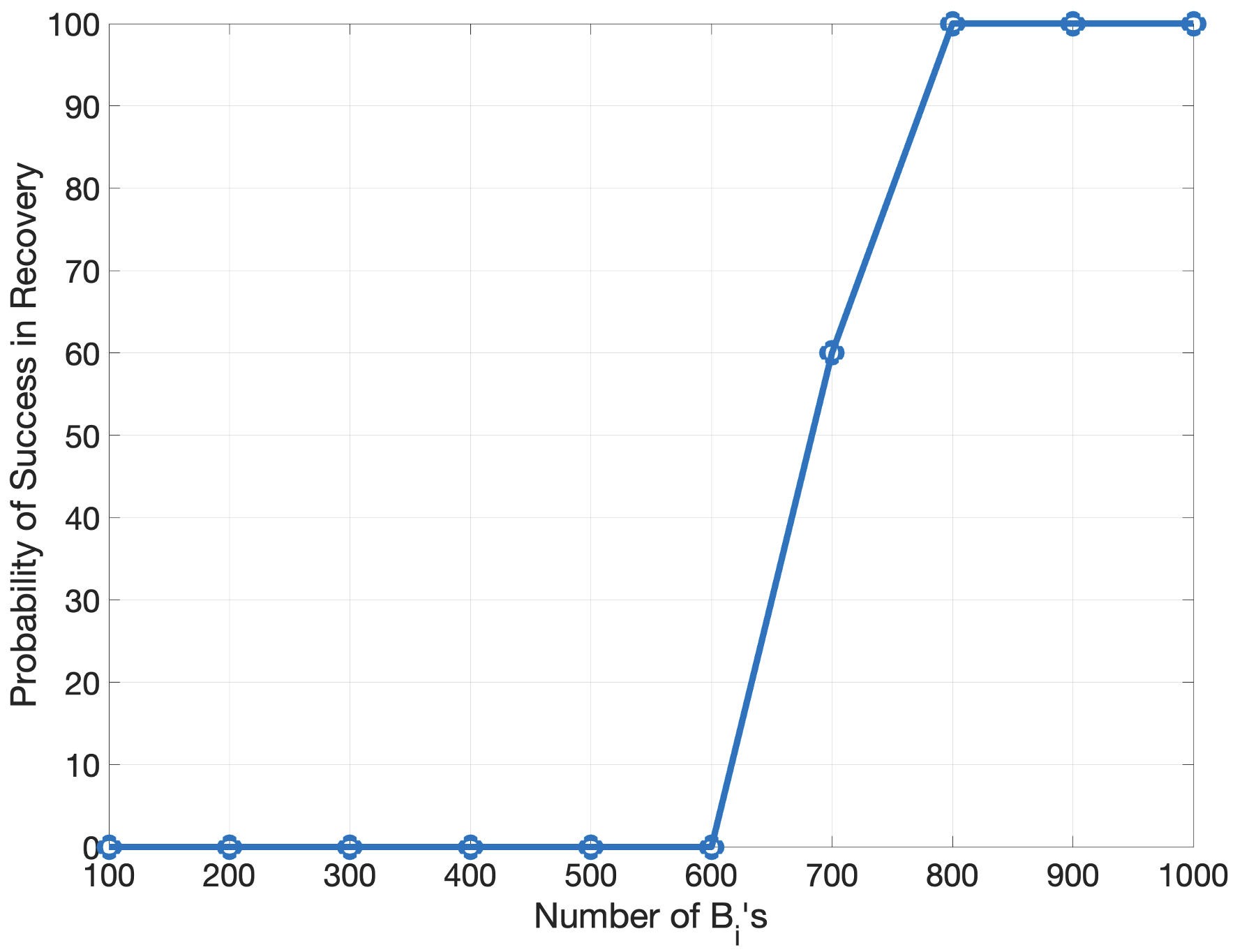
Real-numbered error correction codes leverage Linear Programming (LP) to define constraints on network parameters, ensuring maintained performance even with computational or memory errors. The LP formulation optimizes for robustness by establishing a feasible region of parameter values that satisfy performance criteria despite the introduction of perturbations. Experiments demonstrate the capability of these codes to correct up to 210 errors within a 5120-parameter output layer, indicating a significant level of fault tolerance achieved through this constrained optimization approach. The number of correctable errors is directly tied to the dimensionality of the parameter space and the constraints imposed by the LP solver.

Recovery success rate increases with the number of constraint matrices <span class="katex-eq" data-katex-display="false">\mathbf{B}_{j}</span> utilized, demonstrating the effectiveness of this approach. — Recovery success rate increases with the number of constraint matrices $\mathbf{B}_{j}$ utilized, demonstrating the effectiveness of this approach.

Network Foundations: Leveraging Feedforward Architectures for Robustness

Feedforward Neural Networks (FNNs) provide the foundational structure for implementing error correction codes due to their capacity for non-linear function approximation and parallel processing. These networks consist of multiple layers of interconnected nodes, where information flows in a single direction – from input to output – without cycles. Each connection possesses a weight, and nodes apply an activation function to the weighted sum of their inputs, enabling the network to learn complex relationships. The layered architecture allows for hierarchical feature extraction and representation, crucial for encoding and decoding error correction signals. Specifically, the network learns to map corrupted input data to the original, error-free data by adjusting the weights and biases through training algorithms like backpropagation, effectively functioning as a trainable error correction mechanism.

The functionality of feedforward neural networks for error correction relies heavily on three core elements: the weight matrix, bias terms, and activation functions. The weight matrix, a set of numerical values, determines the strength of connections between neurons in adjacent layers, directly influencing the network’s ability to learn and correct errors. Bias terms, added to the weighted sum of inputs, allow the network to shift the activation function, improving its flexibility. Activation functions, such as ReLU ( $f(x) = max(0, x)$ ) and Leaky ReLU ( $f(x) = max(\alpha x, x)$ , where α is a small positive constant), introduce non-linearity, enabling the network to model complex relationships within the data and, consequently, improve error correction performance. The specific values within these matrices and terms are adjusted during the training process to optimize the network’s accuracy.

The application of L1 and L2 norms during the training of error correction codes within feedforward neural networks serves to regulate the magnitude of the weight matrices. L1 normalization, utilizing the sum of the absolute values of weights, encourages sparsity by driving some weights to zero, effectively simplifying the model and reducing overfitting. Conversely, L2 normalization, employing the sum of the squared values of weights, penalizes large weights, promoting a more distributed representation and improving generalization. Both norms contribute to training stability by preventing excessively large weights that could lead to gradient explosion or oscillations, ultimately ensuring more efficient convergence and robust error correction performance. $L_1 = \sum_{i=1}^{n} |w_i|$ and $L_2 = \sum_{i=1}^{n} w_i^2$ , where $w_i$ represents the individual weights in the network.

Validation and Performance: Demonstrating Resilience on Standard Benchmarks

The application of novel error correction techniques to the WideResNet-22-8 architecture yields significant improvements in model robustness, as demonstrated through testing on the CIFAR-10 dataset. This specific network configuration, when paired with these corrections, establishes a strong baseline accuracy of 93.18%. This performance indicates a heightened ability to maintain predictive accuracy even when confronted with noisy or corrupted input data, suggesting the techniques effectively mitigate the impact of potential errors during image classification. The achieved accuracy not only validates the efficacy of the error correction methods but also positions WideResNet-22-8 as a reliable model for image recognition tasks requiring resilience and precision.

The implementation of Batch Normalization and Dropout consistently improves a model’s ability to generalize beyond the training dataset and maintain stability throughout the learning process. Batch Normalization normalizes the activations of each layer, reducing internal covariate shift and allowing for higher learning rates, while Dropout randomly deactivates neurons during training. This forces the network to learn more robust features that aren’t overly reliant on any single neuron, effectively preventing overfitting and promoting a more distributed representation. Consequently, these techniques lead to models that perform more reliably on unseen data, demonstrating enhanced predictive power and a reduced susceptibility to noise or variations within the input.

Sharpeness-Aware Minimization (SAM) represents a refinement of the conventional optimization process employed in machine learning, moving beyond simply minimizing training loss to actively seeking models with flatter, broader minima in the loss landscape. This approach isn’t about finding the absolute lowest point, but rather identifying solutions that are less sensitive to perturbations in the input data. By encouraging the model to maintain similar performance even with slight variations, SAM inherently builds resilience against adversarial attacks and improves generalization to unseen data. The technique accomplishes this by calculating the gradient not only at the current parameter values, but also at a neighboring set of parameters, effectively exploring the local curvature of the loss function and nudging the optimization towards regions of higher stability. Consequently, models trained with SAM demonstrate improved accuracy and robustness, requiring less fine-tuning and exhibiting more consistent performance across diverse datasets.

Towards Robust and Reliable AI Systems: A Vision for the Future

The handwritten digit dataset, MNIST, continues to serve as a crucial benchmark in the field of artificial intelligence, demonstrating significant progress in error resilience. Recent studies utilizing this dataset have achieved a test classification accuracy of 96.41%, a notable figure enhanced by the implementation of error correction techniques. This performance indicates a growing capacity for AI systems to not only recognize patterns but also to maintain accuracy even when confronted with noisy or imperfect data. The continued use of MNIST allows researchers to refine algorithms and assess the effectiveness of new error-handling strategies in a controlled environment, ultimately contributing to the development of more reliable and trustworthy AI applications.

The pursuit of dependable artificial intelligence receives a significant boost from recent advancements demonstrating improved error resilience. This work establishes a foundation for building AI systems capable of maintaining functionality even when confronted with imperfect or adversarial data-a critical requirement for deployment in high-stakes environments like autonomous vehicles, medical diagnostics, and financial modeling. By proactively addressing vulnerabilities to errors, these developments move beyond simply achieving high accuracy on benchmark datasets, instead prioritizing consistent and reliable performance in real-world conditions. The potential impact extends to fostering greater public trust in AI technologies and enabling their safe and effective integration into increasingly complex aspects of daily life.

Further advancements in the creation of resilient artificial intelligence necessitate a careful consideration of the inherent compromises between system robustness, operational performance, and computational demands. While increasing a system’s ability to withstand adversarial attacks or noisy data is crucial, such improvements often come at the expense of processing speed and require significantly more computational resources. Future research will need to meticulously map these trade-offs, investigating methods to maximize reliability without incurring prohibitive costs. This includes exploring novel algorithmic designs, efficient hardware implementations, and adaptive strategies that dynamically balance robustness and performance based on the specific application and available resources. Ultimately, the goal is not simply to build error-proof AI, but to engineer systems that offer an optimal balance of dependability, speed, and efficiency for real-world deployment.

The pursuit of robustness in neural networks, as detailed in this work, mirrors the principles of elegant system design. The introduction of real-numbered error correction codes, allowing for detection and correction of both memory and computational errors without escalating model complexity, demonstrates a commitment to simplicity. This approach acknowledges that a system’s behavior is fundamentally dictated by its structure; by carefully constraining network weights with linear programming, the framework proactively addresses potential vulnerabilities. As Linus Torvalds once stated, “Talk is cheap. Show me the code.” This sentiment encapsulates the paper’s focus on a practical, implementable solution to a critical problem in neural network reliability. Good architecture is invisible until it breaks, and only then is the true cost of decisions visible.

Beyond Redundancy

The proposition of real-numbered error correction for neural networks addresses a fundamental tension: the desire for computational efficiency against the inevitability of error. This work offers a compelling demonstration of enhanced robustness, yet it simultaneously highlights the fragility inherent in precisely defined systems. If the network survives on meticulously crafted linear constraints, one suspects the underlying architecture may be overengineered-a beautiful solution to a problem that, ideally, a simpler design would sidestep entirely.

Future investigation must move beyond simply correcting errors. The real challenge lies in understanding how errors propagate through network structure, and whether specific architectural motifs are intrinsically more resilient. Modularity, so often touted as a path to control, proves illusory without a deep understanding of inter-component dependencies. A truly robust system doesn’t merely fix mistakes; it anticipates and absorbs them, distributing failure gracefully.

The exploration of real-valued constraints opens intriguing possibilities. Could similar principles be applied to other aspects of network training-regularization, optimization-to create self-healing algorithms? Or is this a temporary fix, a sophisticated bandage on a deeper wound? The elegance of this approach suggests a path forward, but it is a path that demands a holistic view – a recognition that the whole is, demonstrably, more than the sum of its error-corrected parts.

Original article: https://arxiv.org/pdf/2602.00076.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/