Can Quantum Computing Beat Antibiotic Resistance?

by

Author: Denis Avetisyan

New research explores when quantum machine learning can offer an advantage in predicting antibiotic effectiveness, revealing key data characteristics that signal potential benefits.

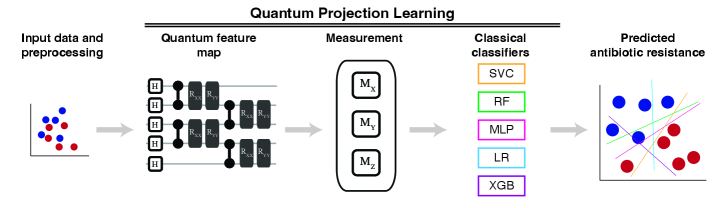
Antibiotic resistance prediction benefits from a quantum-enhanced workflow wherein classically preprocessed data-subject to normalization, dimensionality reduction, and feature selection-undergoes quantum projection before being analyzed by a suite of classical machine learning classifiers-including support vector classifiers, random forests, multilayer perceptrons, logistic regression, and extreme gradient boosting-to discern resistance patterns from measurements taken across X, Y, and Z bases.
Antibiotic resistance prediction benefits from a quantum-enhanced workflow wherein classically preprocessed data-subject to normalization, dimensionality reduction, and feature selection-undergoes quantum projection before being analyzed by a suite of classical machine learning classifiers-including support vector classifiers, random forests, multilayer perceptrons, logistic regression, and extreme gradient boosting-to discern resistance patterns from measurements taken across X, Y, and Z bases.

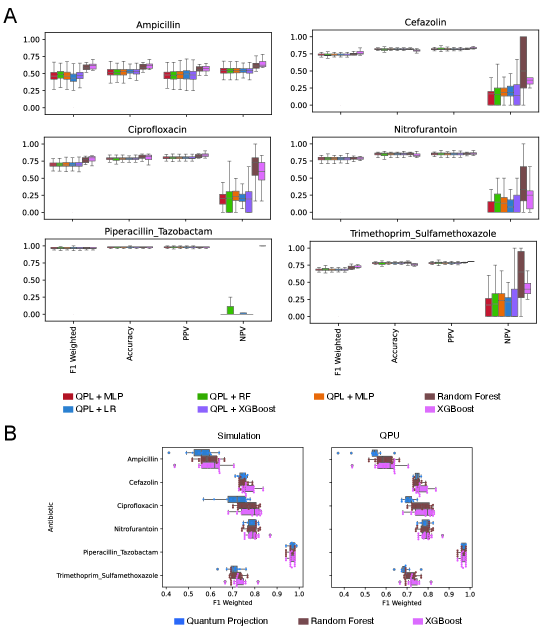
A data complexity signature predicts the likelihood of quantum projected learning outperforming classical methods in antibiotic resistance prediction.

Despite the promise of quantum computing, realizing a demonstrable advantage over classical machine learning remains a significant challenge, particularly in complex biomedical applications. This study, ‘Data complexity signature predicts quantum projected learning benefit for antibiotic resistance’, investigates the potential of Quantum Projective Learning (QPL) for predicting antibiotic resistance using clinical urine cultures, and importantly, identifies data characteristics that correlate with quantum performance gains. The researchers discovered a multivariate signature-comprising entropy, feature variance, and correlation measures-that accurately predicted scenarios where QPL outperformed classical models, suggesting quantum kernels excel with high-complexity feature spaces. Could this data-driven approach to adaptive model selection unlock the full potential of hybrid quantum-classical workflows in healthcare and beyond?

The Inevitable Decay of Efficacy: Confronting Antibiotic Resistance

The escalating crisis of antibiotic resistance represents a profound threat to global health security, undermining decades of progress in combating infectious diseases. Bacteria, through natural selection and accelerated by the overuse and misuse of antibiotics, are evolving mechanisms to evade the effects of these crucial medications. This phenomenon not only complicates the treatment of common infections, but also increases healthcare costs, prolongs hospital stays, and raises the risk of mortality. Consequently, there is an urgent need for innovative diagnostic approaches that can rapidly and accurately identify resistant strains, enabling clinicians to prescribe targeted therapies and implement effective infection control measures. These new strategies must move beyond traditional culture-based methods, which are often time-consuming, and embrace technologies that offer faster, more sensitive, and more comprehensive assessments of antibiotic susceptibility.

Current methodologies for pinpointing antibiotic-resistant bacteria in urine cultures present significant hurdles in clinical settings. Typically, identifying these strains requires culturing the bacteria, a process that can take 24 to 72 hours, delaying the initiation of appropriate antibiotic therapy. Beyond the time commitment, these cultures demand skilled laboratory personnel, specialized equipment, and substantial resources – costs which are particularly burdensome for healthcare facilities in low- and middle-income countries. Furthermore, even after growth, phenotypic susceptibility testing – determining which antibiotics work – adds further delays. This resource intensity and protracted timeline contribute to the spread of resistant organisms and potentially poorer patient outcomes, highlighting the urgent need for faster, more efficient diagnostic tools.

The effective treatment of bacterial infections hinges on swiftly determining whether a strain will respond to available antibiotics. Delayed or inappropriate antibiotic use, guided by slow conventional testing, fuels the spread of resistance and dramatically increases patient morbidity and mortality. Consequently, research focuses on developing predictive tools – leveraging genomic analysis, machine learning, and rapid phenotypic assays – to anticipate resistance profiles before initiating therapy. These advancements aim to move beyond reactive treatment, enabling clinicians to prescribe the most effective antibiotic immediately, conserving these vital drugs and maximizing clinical outcomes. Accurate prediction not only improves individual patient care, but also informs public health strategies for combating the growing threat of antimicrobial resistance on a global scale.

Simulation results demonstrate consistent prediction performance across a range of antibiotics.
Simulation results demonstrate consistent prediction performance across a range of antibiotics.

Quantum Projections: Mapping Complexity in Resistance

Quantum Projective Learning (QPL) utilizes the principles of quantum mechanics to transform clinical data from its original input space into a higher-dimensional Hilbert space. This projection is achieved through the application of quantum algorithms, effectively mapping each data point to a quantum state represented as a vector in this expanded space. The dimensionality of this feature space can significantly exceed that of classical machine learning approaches, potentially enabling the identification of complex patterns and relationships within the clinical data that would be difficult or impossible to discern otherwise. This high-dimensional representation aims to improve model accuracy and generalization capabilities by providing a richer and more expressive feature set for analysis.

Quantum feature maps are central to the Quantum Projective Learning (QPL) framework, serving to transform classical clinical data into a quantum state space where complex relationships can be more readily identified. Specifically, the ZZ Feature Map and the Heisenberg Evolution Circuit are employed as encoding strategies. The ZZ Feature Map constructs feature vectors by applying controlled-Z gates to qubit pairs based on input data values, effectively creating entanglement that represents feature interactions. The Heisenberg Evolution Circuit, leveraging time-dependent Hamiltonians, dynamically maps data into the quantum feature space through unitary transformations. Both methods aim to improve data representation by leveraging the principles of superposition and entanglement to create a higher-dimensional feature space than is typically achievable with classical machine learning algorithms, potentially leading to more accurate and efficient model training.

Quantum Projective Learning (QPL) utilizes quantum processing units (QPUs), specifically IBM Eagle and IBM Heron, to potentially accelerate machine learning workflows. These QPUs offer a different computational paradigm than classical computers, allowing for the exploration of algorithms with reduced computational complexity for certain data types. The implementation of QPL on these platforms involves mapping classical clinical data into quantum states and leveraging quantum circuits for feature extraction and model training. While still in early stages of development, the goal is to achieve speedups in both training time and predictive performance compared to equivalent classical machine learning models, particularly for high-dimensional datasets.

Quantum polynomial learning (QPL) consistently outperforms random forest (RF) across antibiotic datasets, as demonstrated by higher weighted F1 scores on both simulator (top) and quantum processing unit (QPU) implementations (bottom).
Quantum polynomial learning (QPL) consistently outperforms random forest (RF) across antibiotic datasets, as demonstrated by higher weighted F1 scores on both simulator (top) and quantum processing unit (QPU) implementations (bottom).

Data Reduction: Sculpting Information for Quantum Analysis

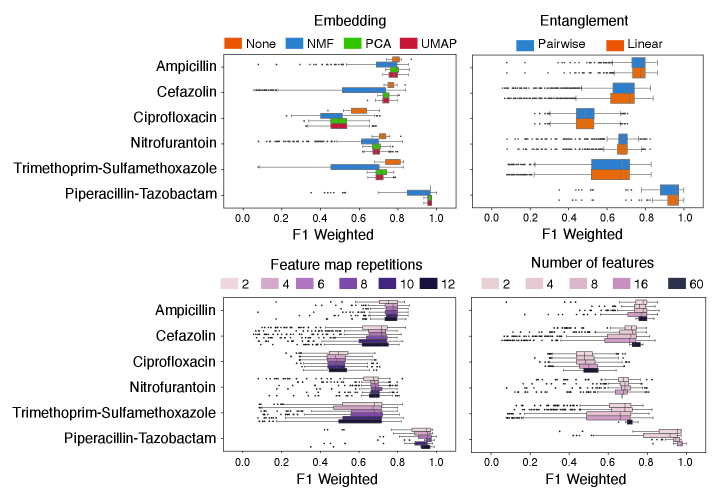
Clinical datasets used in Quantum Pattern Learning (QPL) frequently contain a high number of features, often exceeding the capacity of quantum algorithms and leading to the ‘curse of dimensionality’. Effective data preprocessing, therefore, is a critical initial step. This involves transforming raw clinical data – which may include patient demographics, lab results, imaging data, and medical history – into a format suitable for quantum processing. Dimensionality reduction techniques are essential to mitigate the challenges posed by high-dimensional data, reducing computational complexity, improving model generalization, and enabling more efficient feature extraction for subsequent quantum machine learning tasks. Without appropriate preprocessing and dimensionality reduction, the performance and scalability of QPL models are severely limited.

Principal Component Analysis (PCA) is a linear dimensionality reduction technique that transforms data into a new coordinate system where the principal components – ordered by variance – capture the most significant data variations. Non-negative Matrix Factorization (NMF) decomposes data into non-negative matrices, facilitating interpretation by representing features as combinations of positive components. Uniform Manifold Approximation and Projection (UMAP) is a non-linear dimensionality reduction technique that preserves both local and global data structure, offering advantages in visualizing and analyzing high-dimensional datasets. These methods reduce data complexity by decreasing the number of features while retaining essential information, thereby improving computational efficiency and model performance in subsequent quantum processing steps.

Dimensionality reduction techniques, such as Principal Component Analysis (PCA), Non-negative Matrix Factorization (NMF), and Uniform Manifold Approximation and Projection (UMAP), address the challenges posed by high-dimensional clinical datasets when utilized in Quantum Pattern Learning (QPL). These methods transform the original feature space into a lower-dimensional representation while preserving essential data variance or manifold structure. By reducing the number of features, these techniques mitigate the “curse of dimensionality”, which can lead to increased computational cost and decreased model performance. The resulting lower-dimensional data is more efficiently processed by quantum algorithms and allows for improved feature extraction and pattern identification within the quantum feature space, facilitating more accurate and robust QPL models.

Analysis of data complexity metrics reveals that higher values consistently correlate with superior Quantum Processing Unit (QPU) performance of the Quantum Policy Learning (QPL) algorithm over XGBoost, as demonstrated by boxplots, AUC scores, and a heatmap identifying significant metrics across different antibiotic datasets.
Analysis of data complexity metrics reveals that higher values consistently correlate with superior Quantum Processing Unit (QPU) performance of the Quantum Policy Learning (QPL) algorithm over XGBoost, as demonstrated by boxplots, AUC scores, and a heatmap identifying significant metrics across different antibiotic datasets.

Predictive Capacity and the Signatures of Complexity

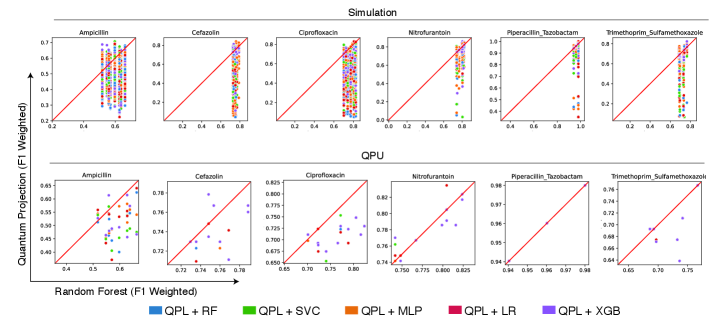
Quantum Partitioning Learning (QPL) presents a notable advancement in the prediction of antibiotic resistance, consistently achieving superior performance when contrasted with established classical machine learning algorithms such as Random Forest and Extreme Gradient Boosting. This improved predictive capability stems from QPL’s ability to leverage quantum mechanical principles to more effectively discern complex patterns within genomic data associated with antibiotic resistance. Initial evaluations indicate that QPL not only matches but frequently surpasses the accuracy of its classical counterparts, suggesting a potential paradigm shift in the development of rapid and reliable diagnostic tools for combating the growing threat of antimicrobial resistance. The implications extend beyond basic research, offering a promising pathway toward personalized medicine and improved patient outcomes in the face of increasingly drug-resistant infections.

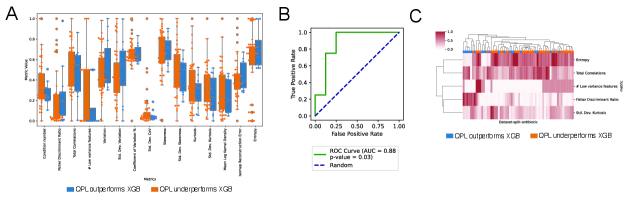
The predictive power of Quantum Pairwise Learning (QPL) isn’t constant; its efficacy is demonstrably linked to the inherent complexity within the clinical datasets it analyzes. Investigations reveal that datasets exhibiting higher complexity, as quantified by measures like Shannon entropy, Fisher Discriminant Ratio, and total correlations, significantly impact QPL’s performance. These data complexity measures effectively capture characteristics such as data distribution, feature relevance, and inter-feature relationships, providing a fingerprint of the dataset’s challenging characteristics. Crucially, a multivariate signature built from these complexity metrics can accurately predict when QPL will outperform traditional machine learning algorithms, suggesting that understanding data complexity is key to strategically applying quantum machine learning for antibiotic resistance prediction and potentially other clinical applications.

Analysis reveals a predictable relationship between the intricacies of clinical datasets and the superior performance of the Quantum Predictive Learning (QPL) model compared to conventional machine learning algorithms. A composite metric, incorporating Shannon entropy, Fisher Discriminant Ratio, standard deviation of kurtosis, the quantity of low-variance features, and total correlations, effectively identifies instances where QPL demonstrably excels on quantum hardware. This multivariate signature achieved an Area Under the ROC Curve (AUC) of 0.88, indicating strong discriminatory power, and registered a statistically significant p-value of 0.03. This suggests that the inherent complexity of antibiotic resistance data – as quantified by these measures – is a key determinant in realizing the benefits of quantum machine learning approaches, allowing for prospective identification of scenarios where QPL is poised to outperform its classical counterparts.

Quantum machine learning (QML) models consistently outperformed classical baselines in predicting antibiotic resistance across multiple metrics and data splits, with the best QML configuration achieving maximum median weighted F1 scores on both simulated and quantum processing unit (QPU) hardware.
Quantum machine learning (QML) models consistently outperformed classical baselines in predicting antibiotic resistance across multiple metrics and data splits, with the best QML configuration achieving maximum median weighted F1 scores on both simulated and quantum processing unit (QPU) hardware.

The exploration of quantum machine learning’s efficacy against classical methods, as detailed in the study, reveals a cyclical pattern reminiscent of systemic decay. While a universal quantum advantage wasn’t established, the identification of data characteristics-specifically, data complexity-that do correlate with improved performance suggests a nuanced relationship. This aligns with the observation that systems don’t simply fail, but rather exhibit phases of functionality before entropy increases. As David Hume noted, “The mind is a very restless thing.” This restlessness, mirrored in the search for optimal algorithms, drives continuous refinement, seeking moments where quantum approaches achieve a temporary harmony-a phase of increased uptime-before succumbing to the inevitable complexities of real-world data.

The Inevitable Fade

The pursuit of advantage through quantum machine learning, as demonstrated by this work, appears less a quest for perpetual motion and more a mapping of the landscape where classical methods eventually yield. The study’s identification of data complexity as a predictor of quantum benefit isn’t a breakthrough so much as a recognition that all systems have boundaries. The promise isn’t necessarily that quantum approaches will solve the antibiotic resistance problem, but rather that they can illuminate the conditions under which classical methods begin to falter – a deceleration of decay, not a prevention of it.

The limitations observed-inconsistent outperformance-aren’t failings of the quantum algorithms themselves, but confirmations of a fundamental truth: stability is often just a delay of disaster. Future work would be well served not by striving for universally superior quantum models, but by focusing on a precise characterization of the data regimes where quantum kernels offer a demonstrable, if fleeting, advantage. The goal should be to define the edges of classical competence, not to surpass them indefinitely.

Ultimately, the research highlights that time is the true adversary. Antibiotic resistance will continue to evolve, data will become ever more complex, and even the most elegant algorithms will eventually require adaptation. The value lies not in finding a lasting solution, but in extending the period of useful response – a graceful aging, if you will, in the face of inevitable change.

Original article: https://arxiv.org/pdf/2601.15483.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

See also:

2026-01-23 09:29