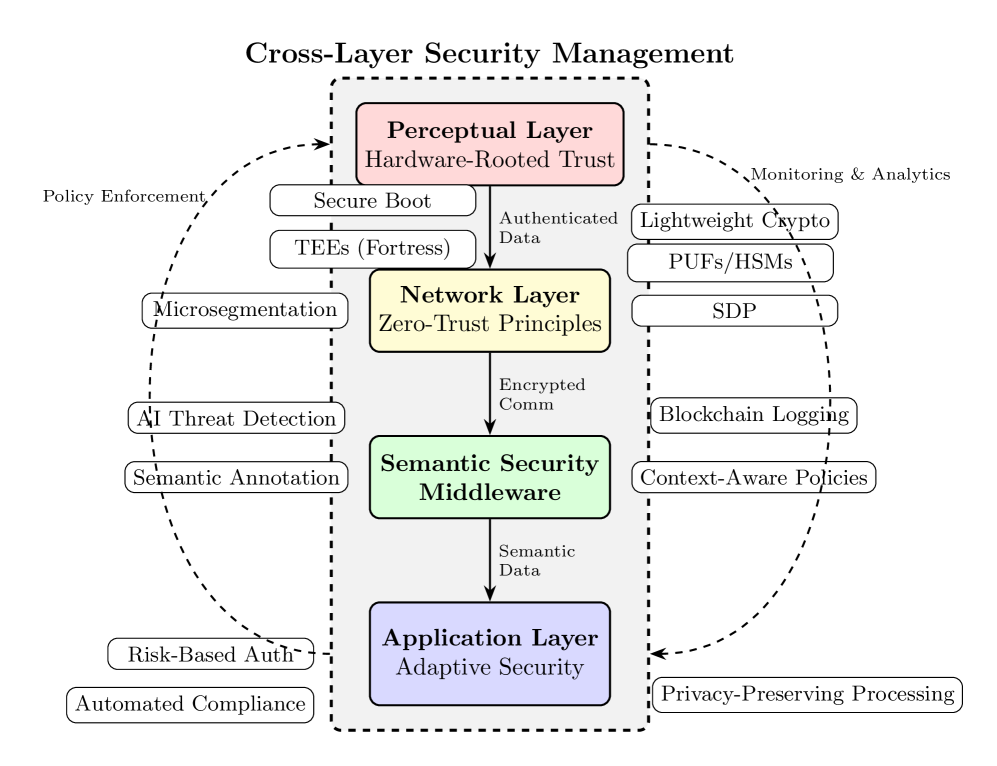
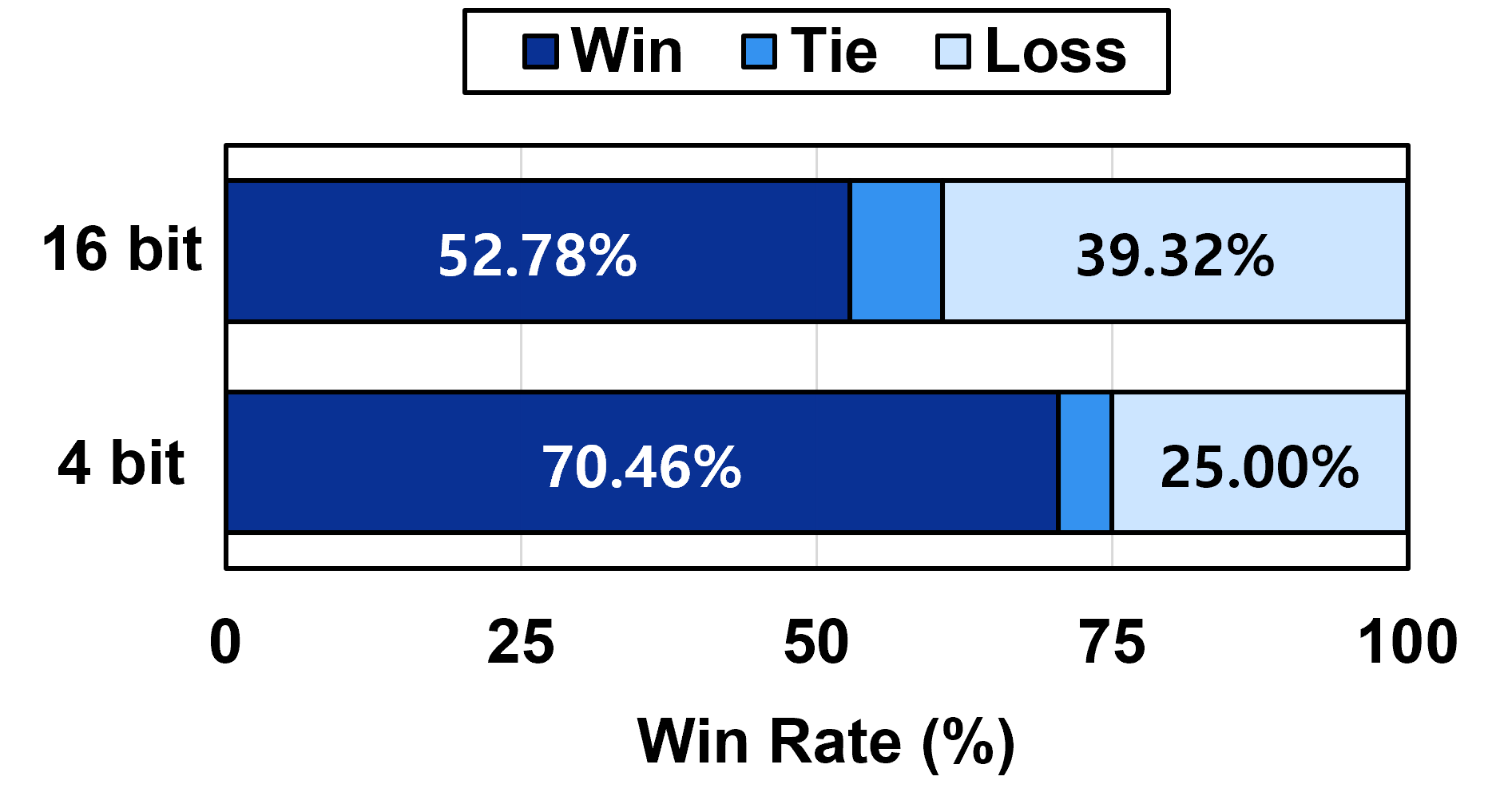
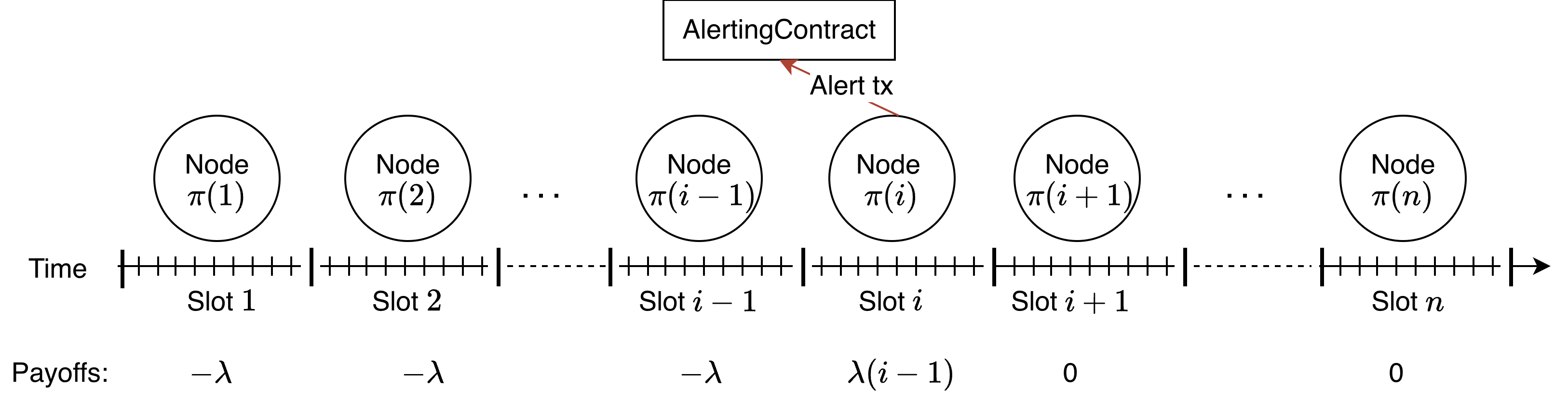
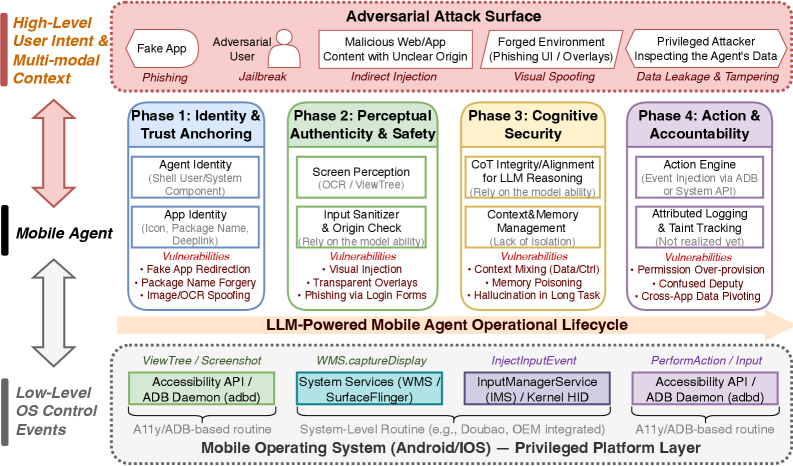
Squeezing the Strong Force: A New Analytical Approach to Femtoscopy
![A square-well potential defines a region where a particle experiences a constant potential energy, effectively confining it within defined boundaries due to the potential difference between the well's interior and exterior [latex] V(x) [/latex].](https://arxiv.org/html/2602.11027v1/figures/img1.jpg)
Researchers have developed a novel analytical solution for modeling the nucleon-nucleon interaction, offering a powerful alternative to computationally intensive methods in femtoscopic studies.
![The study reveals how the sum-rule diagnostics and extracted magnetic dipole moment fluctuate with the Borel mass [latex]M^2[/latex] within the [latex]\bar{u}c[/latex][latex]\bar{u}s[/latex] and [latex]\bar{d}c[/latex][latex]\bar{d}s[/latex] flavor compositions, demonstrating convergence assessed by varying continuum thresholds and pinpointing a working window defined by a minimum 40% pole contribution to ensure reliable magnetic moment calculations.](https://arxiv.org/html/2602.10638v1/x6.png)
![Predictive State Communication (PSC) minimizes transmission overhead by enabling a receiver to speculate on incoming data continuity, requiring the sender to transmit only compact patches to correct errors-a strategy demonstrated by a reduction in innovation load as token rates increase and operation within a feasible rate range defined by starvation and capacity limits-rather than full retransmissions, thereby optimizing communication efficiency as governed by [latex] \text{innovation load} [/latex] and [latex] \text{token rate} [/latex].](https://arxiv.org/html/2602.10542v1/x2.png)