Entangled Agents: Coordinating Without Communication
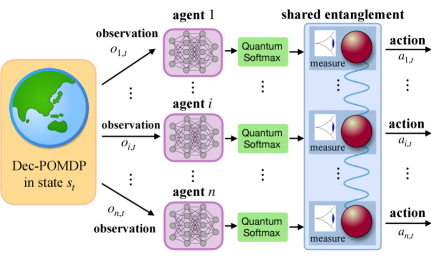
A new framework leverages the principles of quantum entanglement to enable multi-agent systems to coordinate effectively without explicit communication channels.

A new framework leverages the principles of quantum entanglement to enable multi-agent systems to coordinate effectively without explicit communication channels.
![The effective number of configurations, [latex] eSe^{S} [/latex], shifts with coupling strength, diverging within specific intervals and demonstrating a sensitivity to perturbative order-a phenomenon suggesting the model's predictive power is not uniform across all parameter regimes.](https://arxiv.org/html/2602.08265v1/x4.png)
Researchers have developed a novel stochastic method that promises to significantly improve the accuracy and reliability of calculations in complex quantum systems.
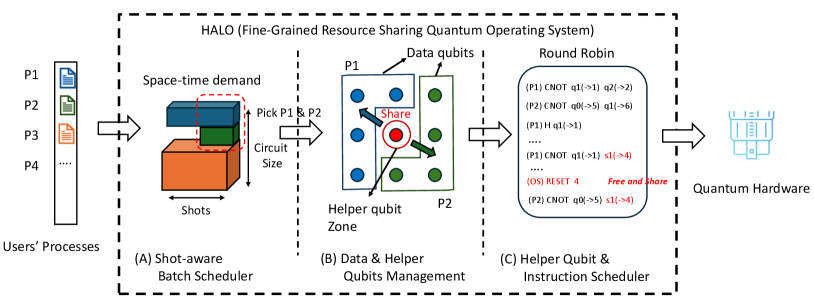
A new quantum operating system, HALO, dramatically boosts performance by enabling precise control and allocation of quantum resources.
A new method tackles the inefficiencies of diffusion language model inference by intelligently verifying and revising generated tokens on the fly.
New research reveals a fundamental trade-off governing the effort required to maintain stability in any system, from cellular processes to digital networks.
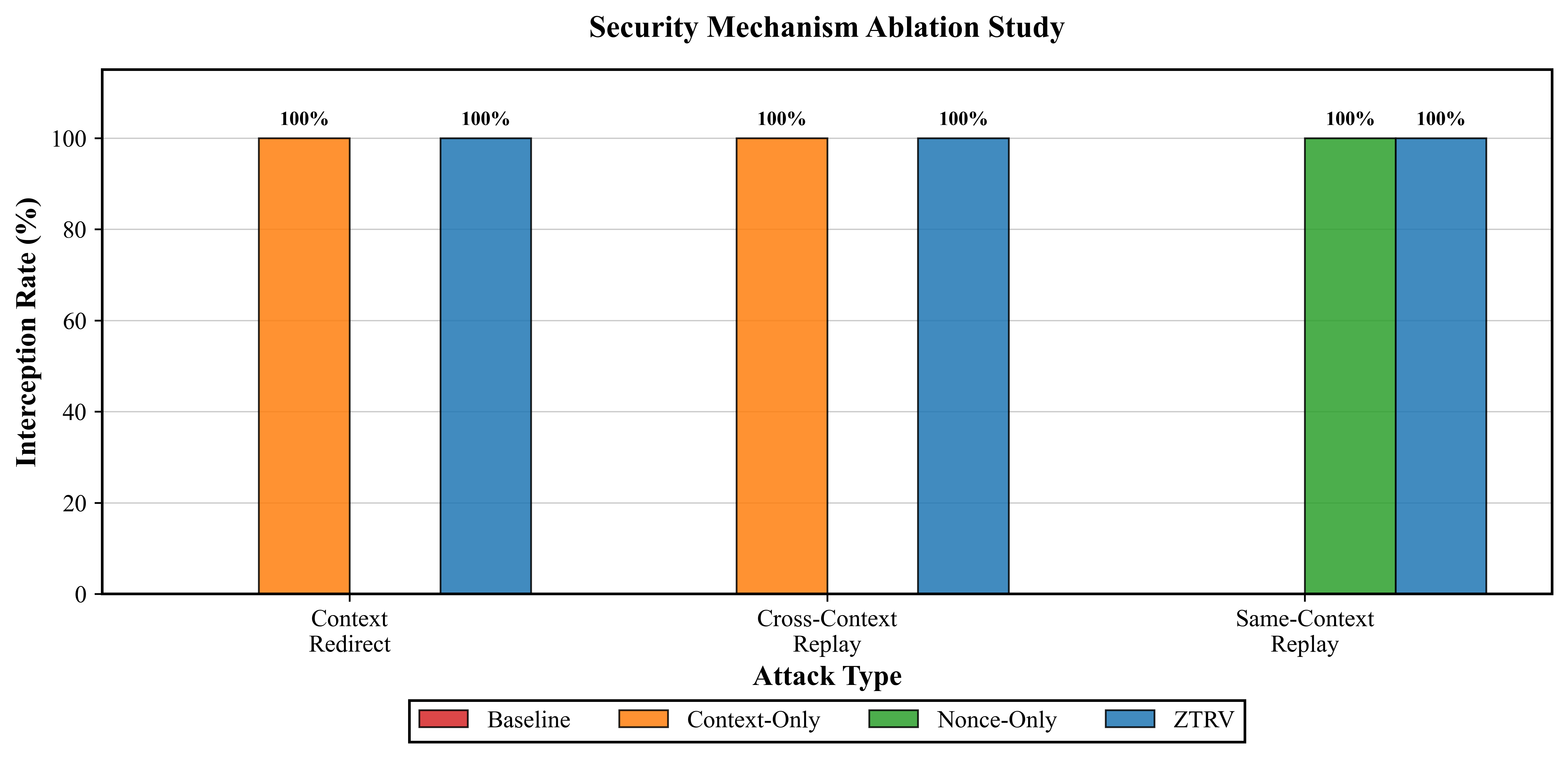
This research introduces a zero-trust runtime verification framework designed to protect agent-driven payment systems from critical vulnerabilities.
A new toolkit reveals widespread flaws in how we evaluate AI’s ability to answer multiple-choice questions, exposing issues from test contamination to simple writing errors.
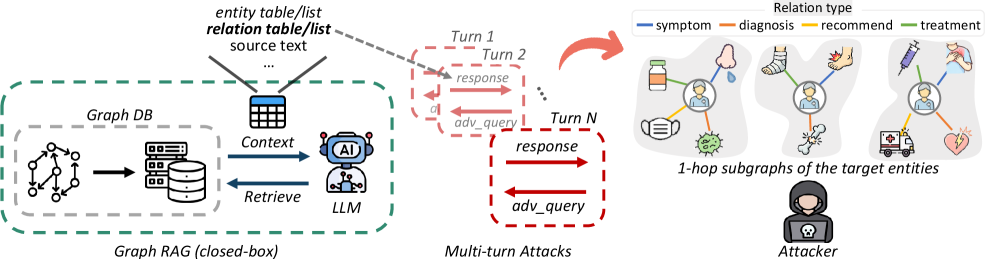
A new study reveals vulnerabilities in Retrieval-Augmented Generation systems built on graph databases, demonstrating how attackers can reconstruct sensitive knowledge from seemingly secure deployments.
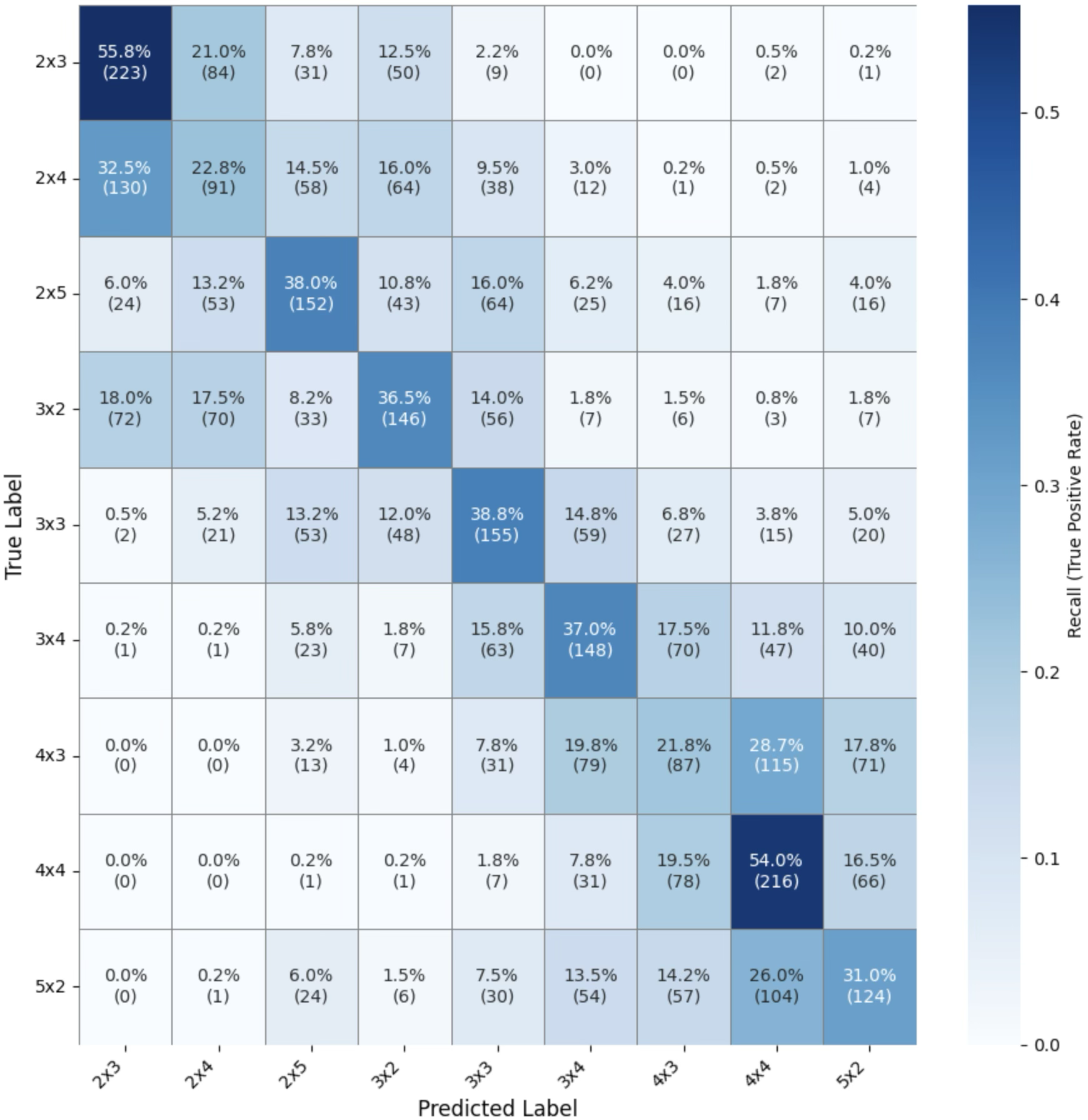
New research reveals how the internal dynamics of large language models evolve during reasoning, offering insights beyond simple token counting.
![The study reveals how adiabatic vibrational energy levels in KCN correlate with Planck’s constant, demonstrating the emergence of diabatic states at avoided crossings-manifested as hyperbolic curves and approximately straight lines-and further clarified through calculations detailed in equations [latex] (3) [/latex] and [latex] (4) [/latex], which differentiate between vibrational states corresponding to K-CN and K-NC linear configurations labeled by diabatic quantum numbers [latex] (n_1, n_2) [/latex].](https://arxiv.org/html/2602.06881v1/x1.png)
A new study uses correlation diagrams to explore how the vibrational spectrum of the KCN molecule transitions from order to chaos as energy increases.