Author: Denis Avetisyan
New research demonstrates that the statistical behavior of key operators in chaotic quantum spin chains aligns with predictions from random matrix theory, suggesting a fundamental level of universality.
Numerical analysis reveals random matrix theory universality for current operators in spin-$S$ Heisenberg chains, supporting thermalization and typicality even at low energies.
While quantum chaotic systems are expected to exhibit universal statistical properties, verifying these predictions at fine energy scales remains a challenge. This is addressed in ‘Random matrix theory universality of current operators in spin-$S$ Heisenberg chains’, where researchers numerically investigate the extent to which operator statistics in translationally invariant Heisenberg spin chains align with random matrix theory. Their analysis of the spin current operator for varying spin quantum numbers provides compelling evidence supporting the conjecture of unitarily invariant ensemble behavior even within narrow energy windows. Do these findings suggest a broader principle of random matrix theory universality governing observable properties across a wider range of quantum chaotic systems?
Decoding Chaos: Navigating Quantum Complexity
The study of complex quantum systems, exemplified by the Heisenberg XXZ Chain, increasingly necessitates a departure from conventional computational methods. Traditional approaches, which attempt to directly simulate the quantum evolution of these systems, quickly become overwhelmed by the exponential growth in computational demands as system size increases. This limitation arises because accurately representing the interconnectedness of many quantum particles requires resources that rapidly exceed even the most powerful supercomputers. Consequently, researchers are actively developing and implementing novel techniques that prioritize statistical analysis and efficient approximation to circumvent these computational bottlenecks, offering a pathway to understand the emergent behavior of these intricate quantum phenomena without being constrained by intractable calculations.
The Heisenberg XXZ chain, and similar quantum systems, aren’t governed by predictable, linear progressions; instead, they demonstrate chaotic behavior, where even minuscule changes in initial conditions can lead to drastically different outcomes. This inherent unpredictability renders traditional computational methods, reliant on precise step-by-step calculations, largely ineffective. Consequently, researchers turn to statistical approaches, focusing not on predicting a single future state, but on characterizing the probabilities of various outcomes. By analyzing the collective behavior of the system over many iterations – or through statistical modeling – it becomes possible to determine average properties, identify dominant trends, and ultimately, understand the system’s evolution without needing to solve the intractable equations governing its precise trajectory. This shift in focus allows for meaningful insights into the system’s long-term behavior, offering a powerful means of navigating the inherent complexity of quantum chaos.
The inherent complexity of quantum systems, such as the Heisenberg XXZ chain, often renders direct calculation of meaningful physical observables-quantities like energy, magnetization, or correlation functions-a practically impossible task. This intractability stems not from a lack of theoretical understanding, but from the exponential scaling of computational resources required to model even moderately sized systems. Consequently, researchers are compelled to develop and implement efficient approximation techniques. These methods, ranging from sophisticated perturbation theory and variational approaches to Monte Carlo simulations and machine learning algorithms, provide pathways to estimate observable values without explicitly solving the full quantum mechanical problem. By sacrificing some degree of precision for computational feasibility, these approximations unlock the ability to probe the behavior of these complex systems and gain insights into their fundamental properties, revealing the emergent phenomena hidden within their quantum nature.
Quantum Typicality: A Statistical Foundation for Many-Body Systems
Quantum Typicality provides a computational shortcut for determining the average value of physical observables in many-body quantum systems. Instead of summing over the entire Hilbert space – a computationally intractable task for large systems – this approach leverages the principle that most pure states are statistically indistinguishable. Specifically, the trace of an operator \hat{O} can be approximated by averaging its matrix elements over a set of Haar-random states, effectively replacing a sum over 2^N states with an average over a much smaller, representative sample. This reduces the computational cost from exponential scaling with system size N to polynomial scaling, making calculations feasible for systems previously inaccessible to direct simulation. The accuracy of this approximation is guaranteed to hold within a specified error bound, dependent on the system’s energy window and the operator in question.
The microcanonical projection is central to quantum typicality as it isolates the system’s behavior within a specific energy range, effectively averaging over states with energies between E and E + \Delta E. This is achieved by projecting the initial state onto the subspace of states with energies within the defined window, yielding an accurate representation of the system’s thermodynamic properties without requiring a full diagonalization of the Hamiltonian. Efficient evaluation of this projection relies on techniques like Chebyshev polynomial expansion to approximate the energy-resolving projection operator, enabling calculations on large Hilbert spaces that would otherwise be intractable. The width \Delta E of the energy window is a critical parameter; a narrower window provides higher resolution but demands more computational effort, while a wider window reduces computational cost at the expense of potentially including irrelevant states.
Chebyshev Polynomials facilitate efficient spectral decomposition by approximating functions on a bounded interval using a series of orthogonal polynomials. This approach avoids direct diagonalization of the Hamiltonian, which is computationally expensive for large systems. The key is to represent the Hamiltonian H as a polynomial in terms of itself, allowing for the calculation of quantities like Tr(f(H)) using recursion relations. Specifically, the Chebyshev polynomials enable the efficient expansion of f(H) and subsequent evaluation of the trace via a weighted sum over a small number of randomly chosen states, dramatically reducing computational complexity compared to traditional methods that require sampling the entire Hilbert space.
Probing Quantum Transport: The Signature of Spin Current
The total spin current operator, denoted as J_s, plays a central role in characterizing quantum transport within the Heisenberg XXZ spin chain. This operator quantifies the flow of spin angular momentum through the system, providing insights into how information and energy are transferred at the microscopic level. Specifically, its statistical properties, such as its variance and higher-order moments, reveal crucial information about the underlying transport mechanisms, distinguishing between ballistic, diffusive, and localized regimes. The XXZ chain, exhibiting both integrable and chaotic phases depending on its anisotropy parameter, provides a valuable testbed for understanding these phenomena; analysis of J_s allows researchers to investigate how quantum chaos impacts transport characteristics and to test theoretical predictions derived from Random Matrix Theory.
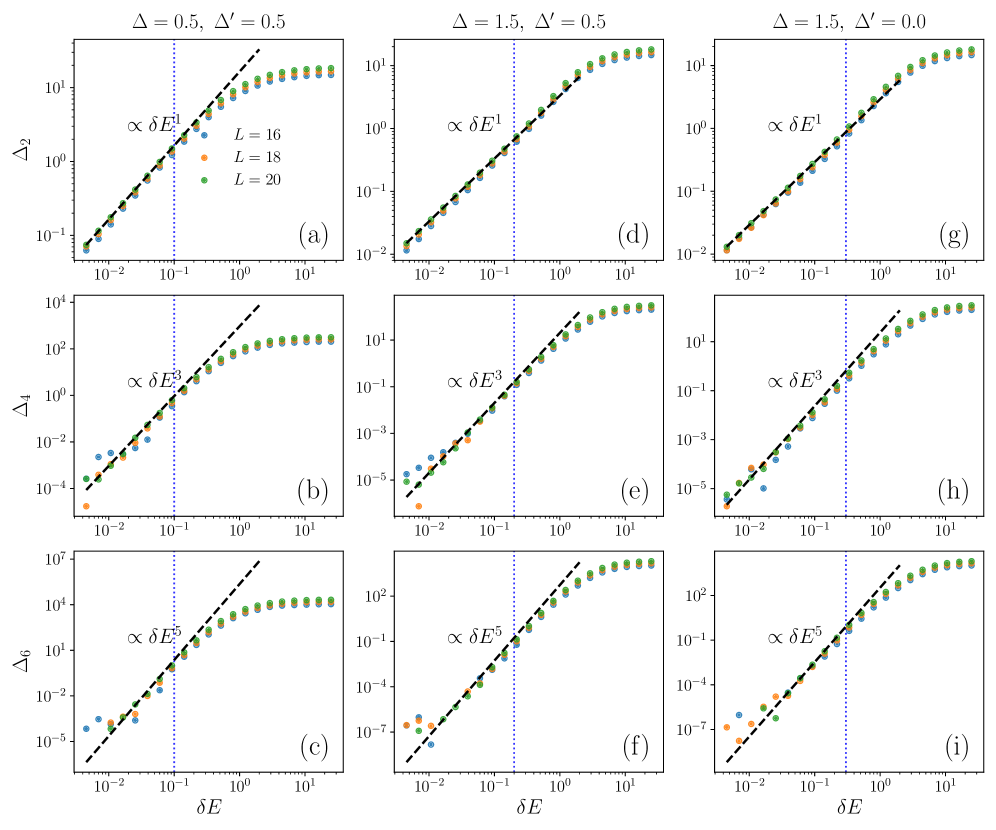
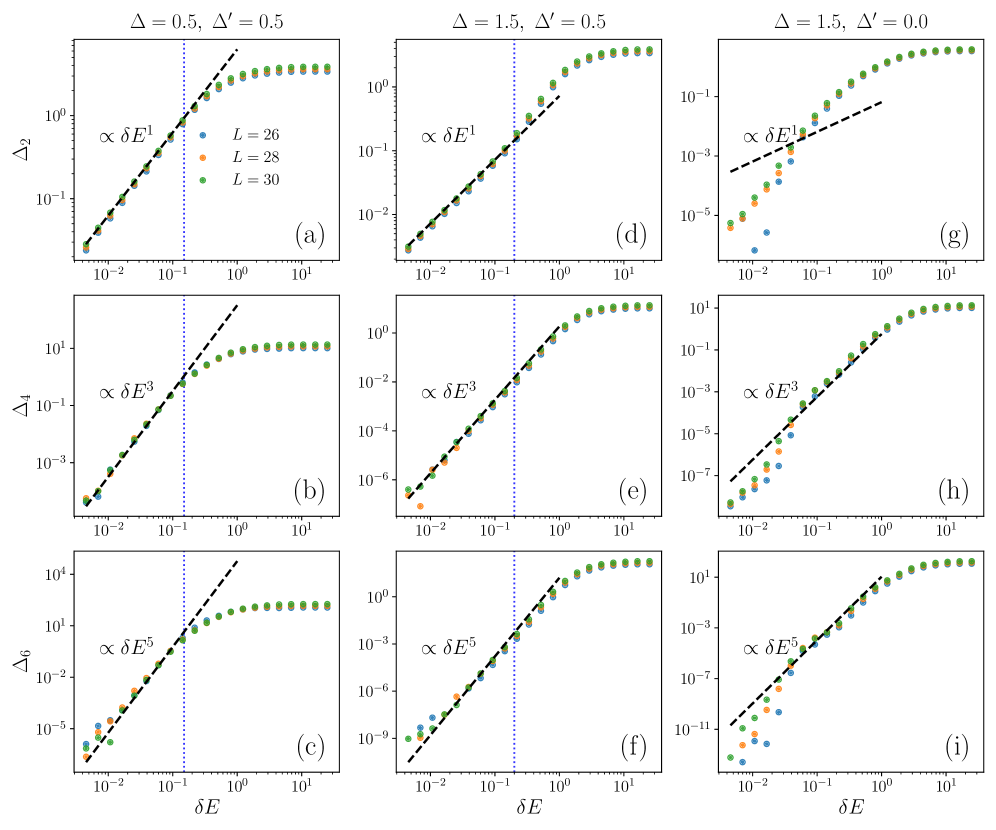
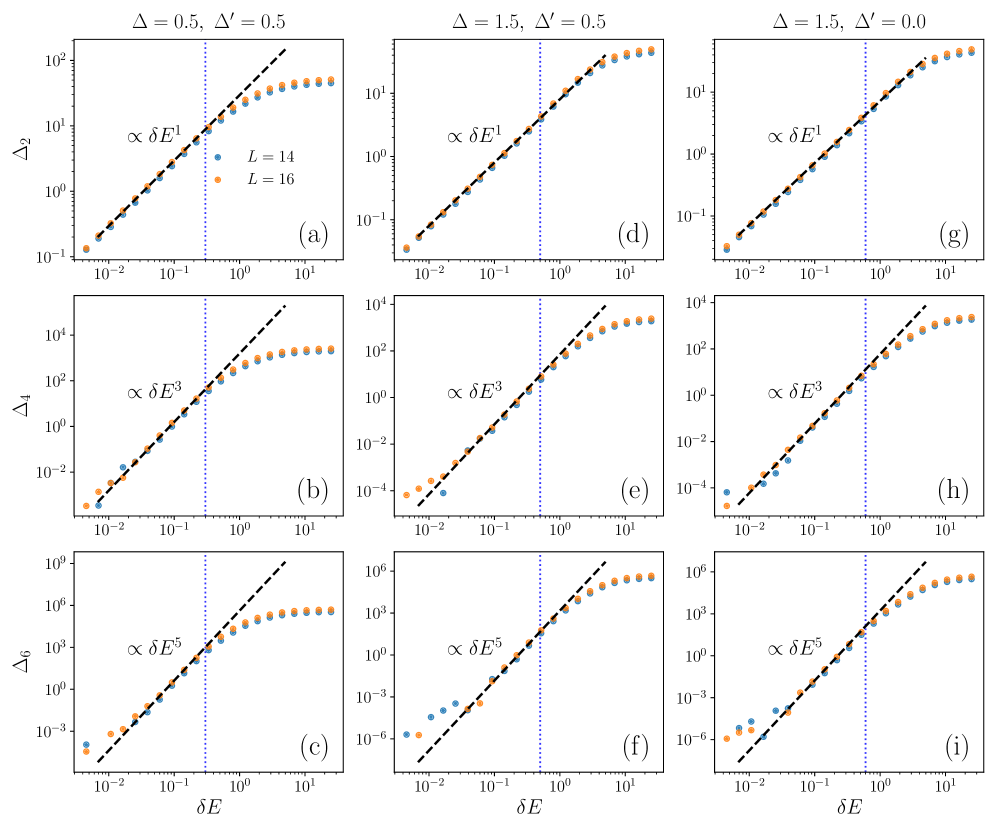
Statistical properties of the Total Spin Current Operator were calculated using the Microcanonical Projection technique, a method justified by the principle of Quantum Typicality. This approach allowed for computations on systems with lengths up to L=30 for spin quantum number S=1/2, L=20 for S=1, and L=16 for S=3/2. These system sizes represent a significant scale for numerical investigation of quantum transport characteristics within the Heisenberg XXZ Chain, providing data for analysis of operator behavior and validation against theoretical predictions.
Verification of the computational approach involves analyzing the scaling behavior of the variance Δk of the total spin current operator using Free Cumulants. Results demonstrate that Δk scales inversely with the energy level spacing δE, specifically as Δk \propto δE^{-1}, within chaotic regimes for spin quantum numbers S=1/2, 1, and 3/2. This scaling behavior is notably absent in integrable systems, which exhibit different variance characteristics. The observed δE^{-1} scaling provides support for the conjecture of Random Matrix Theory (RMT) universality, suggesting that the statistical properties of the total spin current in the chaotic Heisenberg XXZ chain align with predictions derived from RMT.
Harnessing Symmetry: Expanding the Reach of Computation
Computational demands in simulating the Heisenberg XXZ chain, a fundamental model in quantum magnetism, are substantially lessened through the strategic application of symmetry exploitation. The XXZ chain possesses inherent symmetries – notably, conservation of total spin and parity – which, when accounted for, dramatically reduce the effective Hilbert space requiring computation. By focusing calculations only on symmetry-distinct states, researchers avoid redundant evaluations and significantly accelerate simulations. This technique isn’t merely a computational shortcut; it allows investigations of larger system sizes and longer timescales, providing access to the complex, many-body phenomena inaccessible with traditional, symmetry-agnostic approaches. Consequently, symmetry exploitation becomes a cornerstone for exploring the chain’s quantum behavior and validating theoretical predictions regarding its properties and potential applications.
A key advancement in simulating the Heisenberg XXZ chain lies in drastically reducing computational load. By intelligently exploiting the system’s inherent symmetries, researchers can minimize redundant calculations without sacrificing accuracy. This technique doesn’t simply offer a speed boost; it fundamentally expands the scope of possible investigations. Previously intractable systems, limited by exponential scaling of computational resources, become accessible, allowing for the study of larger chains and more intricate interactions. Consequently, the ability to probe these complex systems unlocks deeper insights into quantum many-body physics, offering a pathway to understanding phenomena that were once beyond reach and validating theoretical predictions regarding the behavior of quantum-chaotic systems.
Recent investigations into quantum-chaotic many-body systems reveal a compelling connection between computational techniques and fundamental statistical predictions. By combining the principles of Quantum Typicality – which focuses on the most probable outcomes of quantum systems – with efficient spectral decomposition and symmetry exploitation, researchers demonstrate that operators truncated within a microcanonical ensemble exhibit behavior consistent with Unitarily Invariant Ensembles (UIE). This UIE behavior, observed in chaotic regimes, provides strong evidence supporting the long-standing conjecture of Random Matrix Theory (RMT) universality – suggesting that the statistical properties of complex quantum systems are remarkably independent of the specific details of their underlying structure. Essentially, the observable statistics of these systems align with those predicted by random matrices, implying a universal signature of quantum chaos and offering a powerful tool for understanding the behavior of complex quantum systems.
The study meticulously demonstrates how the statistical properties of spin current operators in Heisenberg chains align with predictions derived from random matrix theory. This convergence isn’t merely coincidental; it suggests a deeper universality at play within these quantum systems. As Jürgen Habermas observed, “The unexamined life is not worth living.” Similarly, the unexamined quantum system yields limited insight; only through rigorous analysis-such as comparing operator statistics to established theoretical frameworks-can one truly understand its behavior. The research confirms that even at relatively low energy levels, these systems exhibit characteristics consistent with quantum chaos, bolstering the principles of quantum typicality and the broader implications of random matrix theory for understanding thermalization.
Beyond the Ensemble
The correspondence between the behavior of spin currents in these Heisenberg chains and the predictions of random matrix theory is compelling, yet feels, in a sense, like identifying a familiar face in a crowd. It confirms a certain universality – a tendency for complex quantum systems to ‘forget’ their specific details and converge on statistically predictable behaviors. However, this convergence begs the question of where this universality breaks down. The current work largely explores the system’s behavior within the microcanonical projection, essentially a snapshot of the system at a fixed energy. The next step necessitates a dynamic perspective; how do these statistical properties evolve with time, and at what point does the system’s initial condition reassert itself, disrupting the ensemble’s smooth predictability?
Furthermore, the exploration has been largely confined to one-dimensional systems. While providing a valuable, analytically tractable playground, the jump to higher dimensions introduces a level of complexity akin to moving from laminar flow to turbulence. Do the same statistical hallmarks of chaos – the level repulsion, the characteristic eigenvalue distributions – persist in these more complex landscapes? Or does the increased dimensionality necessitate a refinement of the random matrix ensembles used to model these systems? Perhaps a new ‘universality class’ awaits discovery, revealing subtle but crucial differences in the signatures of quantum chaos.
Ultimately, this line of inquiry resembles a cartographer charting a coastline. Each confirmation of random matrix theory’s predictions is another landmark identified, but the true shape of the ‘thermal island’ – the region where quantum chaos reigns – remains largely obscured. Future work must focus on pushing the boundaries of these numerical investigations, venturing into unexplored parameter spaces and tackling the formidable challenge of simulating increasingly complex quantum systems.
Original article: https://arxiv.org/pdf/2601.10211.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- Jujutsu Kaisen Modulo Chapter 18 Preview: Rika And Tsurugi’s Full Power
- Upload Labs: Beginner Tips & Tricks
- How to Unlock the Mines in Cookie Run: Kingdom
- ALGS Championship 2026—Teams, Schedule, and Where to Watch
- Top 8 UFC 5 Perks Every Fighter Should Use
- Roblox 1 Step = $1 Codes
- How to Unlock & Visit Town Square in Cookie Run: Kingdom
- Jujutsu: Zero Codes (December 2025)
- USD COP PREDICTION
- Mario’s Voice Actor Debunks ‘Weird Online Narrative’ About Nintendo Directs
2026-01-17 20:28