Decoding Beyond the Poles: A Faster Path for Error Correction

Author: Denis Avetisyan

A new decoding framework leverages the underlying symmetries of polar codes to significantly improve speed and performance in error correction.

Performance metrics demonstrate the capabilities of <span class="katex-eq" data-katex-display="false">\mathsf{POD}</span> when operating with the eBCH(16,7)(16,7) coding scheme, indicating its efficacy within that specific communication architecture. — Performance metrics demonstrate the capabilities of $\mathsf{POD}$ when operating with the eBCH(16,7)(16,7) coding scheme, indicating its efficacy within that specific communication architecture.

Polar Orbit Decoding utilizes automorphism groups to enable universal parallel soft decoding for binary linear block codes transformed into polar form.

Despite the foundational role of binary linear block codes in modern communication, achieving optimal performance across all metrics remains a challenge, often necessitating complex multi-code architectures. This paper introduces ‘Polar Orbit Decoding: Universal Parallel Soft Decoding via Automorphism Orbits’, a novel decoding framework leveraging the automorphism groups of these codes to enable substantial parallelization within a unified polar-style decoder. By decoding over orbits of permutations-maintaining consistent dynamic-frozen constraints-Polar Orbit Decoding achieves significant latency-performance trade-offs without exhaustive searches or frozen-set adaptation. Could this approach pave the way for more efficient and scalable decoding solutions in future communication systems?

The Fragile Foundation of Reliable Transmission

The seamless flow of information in modern digital communication – from streaming video to financial transactions – hinges on the ability to overcome the inherent unreliability of transmission channels. Data, represented as bits, are vulnerable to noise, interference, and signal degradation, leading to errors that can compromise integrity. Consequently, sophisticated error correction techniques are indispensable; these methods add redundancy to the original data, enabling the receiver to detect and correct a certain number of errors without requesting retransmission. This redundancy isn’t merely about adding extra bits, but rather employing mathematically structured codes – like those found in $n$ -dimensional vector spaces – that allow for the reliable reconstruction of the original message, even when corrupted. Without such robust error correction, even minor disturbances could render digital communication unusable, highlighting its critical role in nearly every aspect of contemporary life.

Binary Linear Block Codes (BLBCs) represent a cornerstone of modern digital communication, providing a systematic method for detecting and correcting errors introduced during data transmission. These codes operate by dividing a message into blocks of data and appending redundant bits – known as parity bits – calculated based on the original data. This creates codewords that, even if corrupted during transmission, can be decoded to recover the original message with high probability. The linearity of these codes simplifies both the encoding and decoding processes, making them particularly attractive for implementation in hardware and software. $(n, k)$ notation commonly describes a BLBC, where $n$ represents the total length of the codeword and $k$ denotes the number of data bits; the difference, $n-k$ , signifies the number of parity bits added for error correction. The foundational nature of BLBCs stems from their ability to provide a guaranteed level of error protection, a crucial element in ensuring the reliable delivery of information across noisy communication channels.

While binary linear block codes provide a crucial layer of error correction in digital communication, realizing their benefits isn’t without challenges. The process of decoding these codes – reconstructing the original message from potentially corrupted data – demands significant computational resources. This is particularly true for longer block lengths and more powerful codes designed to correct numerous errors. Consequently, the decoding process can become a performance bottleneck in high-speed communication systems, limiting the overall data throughput. Researchers continually explore algorithmic optimizations and specialized hardware implementations to reduce this computational burden, seeking to balance error correction capability with real-time processing demands. The trade-off between decoding complexity and error-correcting performance remains a central focus in the field, driving innovation towards more efficient and scalable communication technologies.

The eBCH (64, 16) code demonstrates strong performance in error correction.

Polar Codes: Approaching the Limits of Communication

Polar codes represent a significant advancement in error correction due to their provable capacity-achieving characteristic. Unlike traditional codes, which often require approximations to determine performance limits, polar codes are mathematically demonstrated to achieve the Shannon limit – the theoretical maximum rate of reliable communication over a noisy channel – as the code length approaches infinity. This is achieved through a specific code construction that explicitly addresses channel polarization, effectively creating reliable and unreliable communication channels. Consequently, in scenarios where the signal-to-noise ratio (SNR) is sufficiently high, polar codes can theoretically outperform conventional codes like LDPC or Turbo codes, offering improved error correction performance for a given block length and computational complexity. The performance gain is most pronounced in scenarios approaching the Shannon limit, where traditional codes struggle to close the gap between their performance and the theoretical maximum.

The construction of polar codes fundamentally relies on a process termed ‘polar transformation’. This transformation operates on any Binary Linear Block Code (BLBC) – a code defined by its length, the number of data bits, and a generator matrix – to create a polar code equivalent. The transformation involves applying a specific matrix, typically denoted as $G_N$ , to the information bits, effectively creating a set of transformed bits. These transformed bits exhibit strong correlations, which are then exploited during the encoding and decoding processes. Specifically, the transformation aims to create bits that are either completely reliable or completely unreliable, allowing for efficient decoding by focusing on the reliable bits and disregarding the unreliable ones. The resulting polar code maintains the same rate as the original BLBC, but benefits from a structured format that enables low-complexity decoding algorithms.

Successive Cancellation List Decoding (SCLD) is a common decoding algorithm for Polar codes, operating by iteratively estimating the most likely transmitted sequence based on the received data and a list of candidate sequences; however, SCLD’s performance is heavily influenced by the list size $L$ . Larger $L$ values improve error correction capability but significantly increase computational complexity. Optimization strategies for SCLD include employing Cyclic Redundancy Check (CRC) aided decoding to prune incorrect candidates from the list, utilizing ordered statistics decoding to prioritize more likely candidates, and implementing efficient data structures and parallelization techniques to reduce the overall decoding time. Furthermore, research explores variations of SCLD, such as Belief Propagation List Decoding, to potentially improve performance and reduce complexity.

The eBCH (64, 36) code demonstrates strong performance in error correction.

Decoding Through Symmetry: Leveraging Automorphism Groups

Automorphism Ensemble Decoding (AED) provides a method for parallelizing the decoding process of Polar codes by capitalizing on the inherent algebraic structure of the code itself. Traditional Polar decoding relies on sequential operations due to the dependencies between bit-channel decoding stages; AED circumvents this limitation by partitioning the decoding graph based on the symmetries defined by the automorphism group of the code. This allows multiple, independent decoding instances – each operating on a subset of the original decoding graph – to proceed concurrently. The effectiveness of AED is directly related to the size and structure of the automorphism group, and the ability to efficiently map decoding operations to these symmetry-defined partitions, thereby enabling substantial reductions in decoding latency through parallel processing.

The Automorphism Group of a linear code is the set of all permutations that map valid codewords to other valid codewords. Formally, it’s a group under composition, with the identity permutation (leaving all codewords unchanged) as its identity element. This group’s structure is crucial because it reveals inherent symmetries within the code; applying an automorphism to a received word doesn’t alter its information content, enabling parallel processing of multiple transformed versions during decoding. Understanding this group requires defining the operation of permutation on the codewords and verifying that the resulting output remains within the code’s defined structure – i.e., satisfies the code’s defining equations – and that the inverse of each permutation also exists within the group.

Representation of the automorphism group is achieved through computational methods such as the Schreier-Sims algorithm, which systematically constructs the group’s structure by generating a series of permutations. The output of this algorithm is typically expressed as a ‘Base and Strong Generating Set’. The ‘Base’ consists of a minimal set of elements upon which all other group elements can be built, while the ‘Strong Generating Set’ defines a set of permutations that, when combined with elements from the base, can generate any element within the entire automorphism group. Efficiently determining these sets is critical for practical implementation, as they directly dictate the complexity and scalability of parallel decoding algorithms.

Application of the Automorphism Ensemble Decoding method to Reed-Muller codes results in substantial gains in decoding efficiency. Reed-Muller codes, defined by $RM(m,k)$ , possess a well-defined automorphism group that allows for the creation of multiple, independent decoders operating in parallel. This parallelization is achieved by mapping the original decoding problem into multiple sub-problems, each solvable by a decoder representing a specific automorphism. The resulting speedup is directly proportional to the size of the automorphism group and the efficiency of the parallel processing infrastructure, significantly reducing the overall decoding latency compared to sequential decoding approaches. Experimental results demonstrate performance improvements for larger block lengths and higher code rates, particularly in scenarios demanding low-latency communication.

Decoding as Permutation: A Unified Approach with Polar Orbit Decoding

Polar Orbit Decoding introduces a novel approach to decoding Polar codes by harnessing the power of permutation actions. This technique fundamentally shifts the decoding process from a sequential, layer-by-layer operation to a parallel one, significantly accelerating performance. Instead of processing bits individually in a specific order, the algorithm explores multiple decoding paths simultaneously through the application of carefully chosen permutations. This parallel exploration isn’t simply about dividing the workload; it exploits inherent symmetries within the code structure, allowing for a more efficient search for the most likely transmitted message. The core innovation lies in representing the decoding process as an orbit under the action of a permutation group, enabling substantial gains in speed and a reduction in latency, particularly when compared to traditional decoding methods like Successive Cancellation.

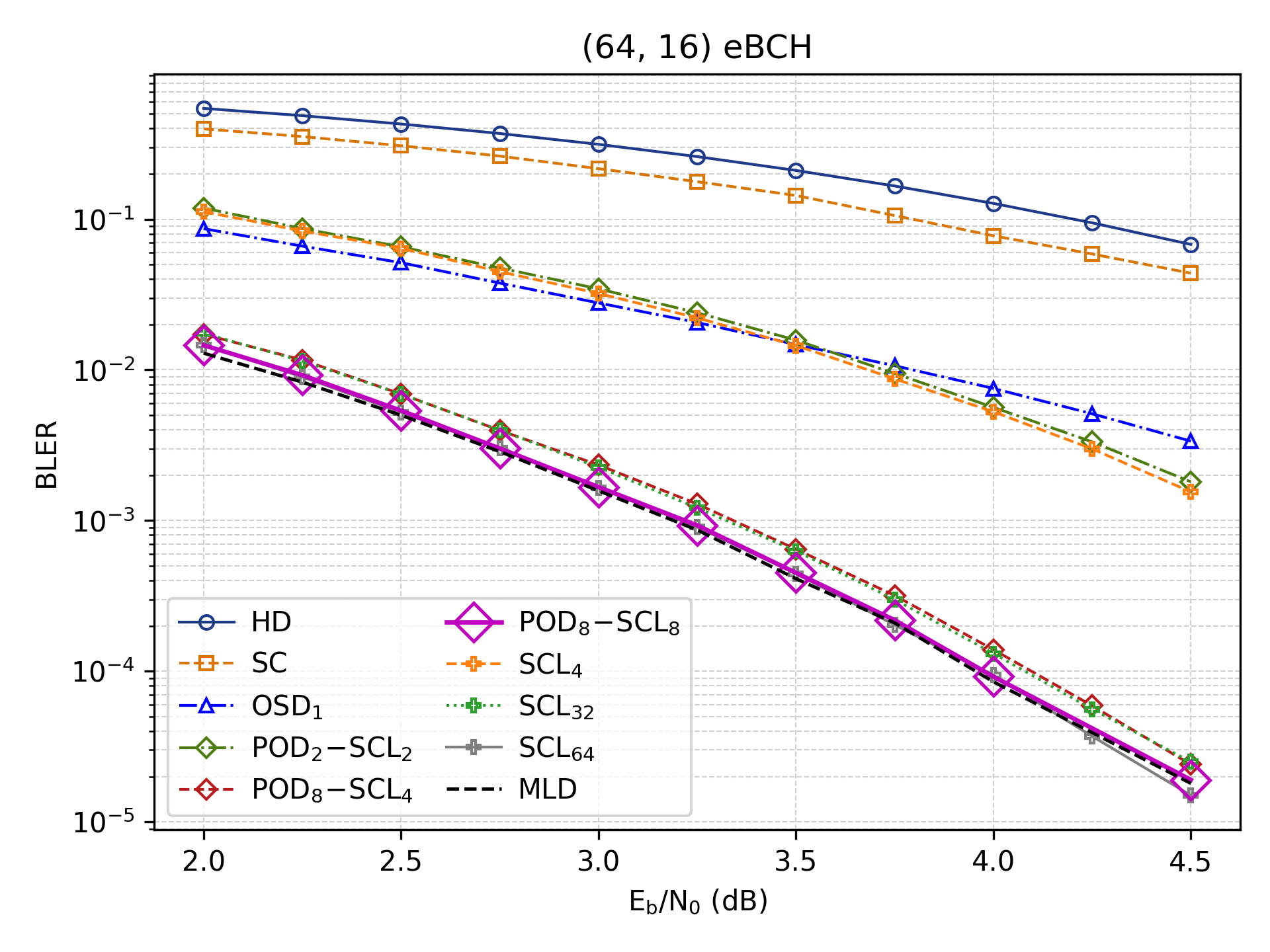
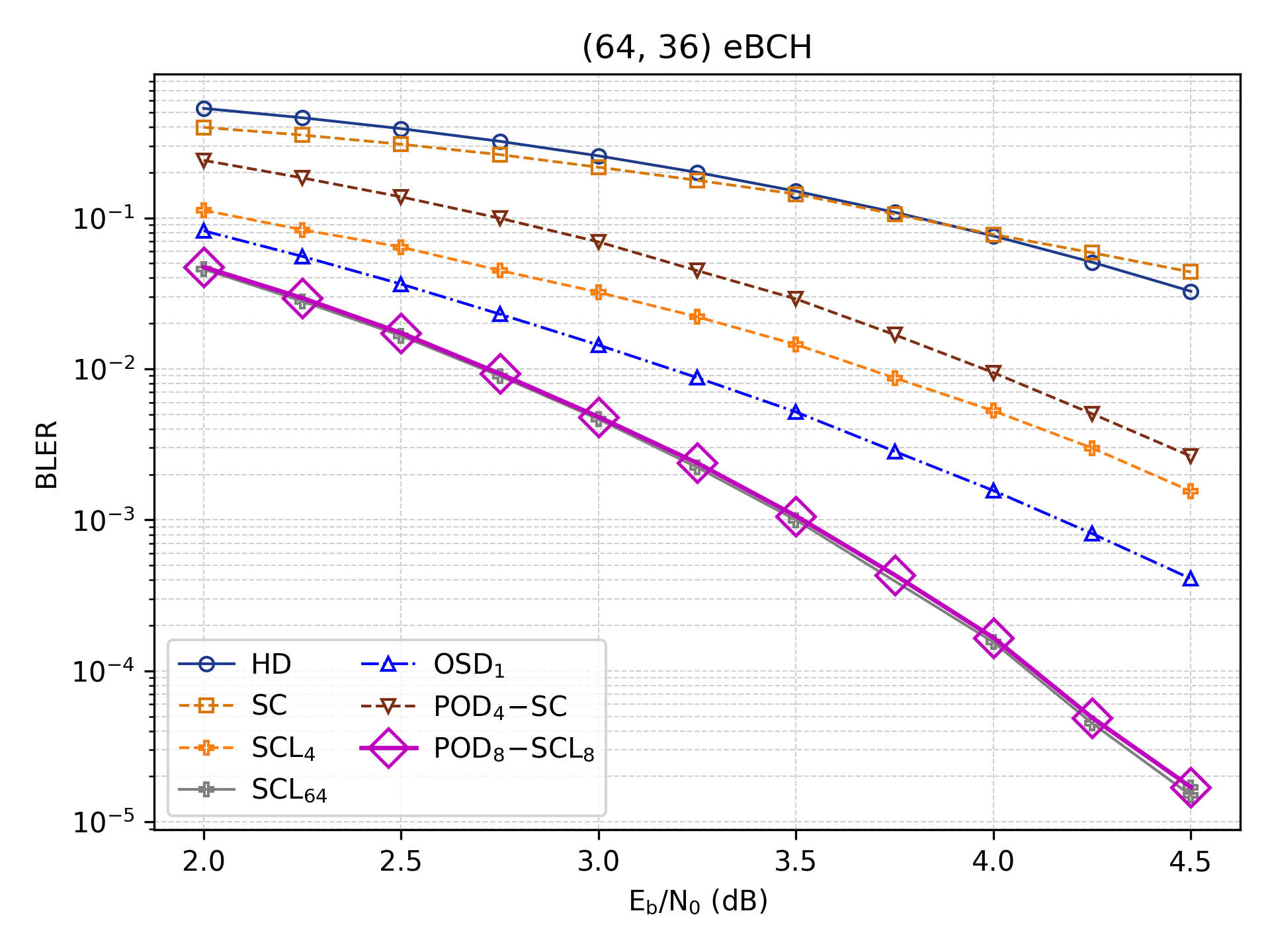
The implementation of Dynamic Frozen Constraints within the Polar Orbit Decoding (POD) framework yields substantial improvements in decoding performance. These constraints, adjusted adaptively during the decoding process, strategically reduce the search space without compromising accuracy. This method effectively prunes unlikely candidate codewords, allowing for faster convergence towards the correct solution. By intelligently managing frozen bits – those with predetermined values – POD minimizes computational complexity and latency. The result is a decoding process that not only achieves near-maximum likelihood performance but also rivals the speed of Successive Cancellation List (SCL) decoding, often with a significantly reduced list size and associated resource demands.

The utility of Polar Orbit Decoding extends significantly beyond its initial application to standard Polar codes, demonstrating a capacity to efficiently decode a broader class of error-correcting codes. Specifically, the framework successfully addresses the complexities of Extended Golay and Extended BCH codes, which traditionally rely on the intricate mathematical structures of the Mathieu Group and Affine Semilinear Group, respectively. By leveraging permutation actions, this approach unlocks parallel decoding capabilities for these codes, bypassing the limitations of sequential decoding methods. This adaptability positions Polar Orbit Decoding as a unified and versatile solution, offering performance gains across diverse coding schemes and opening avenues for optimization in communication systems where code flexibility is paramount.

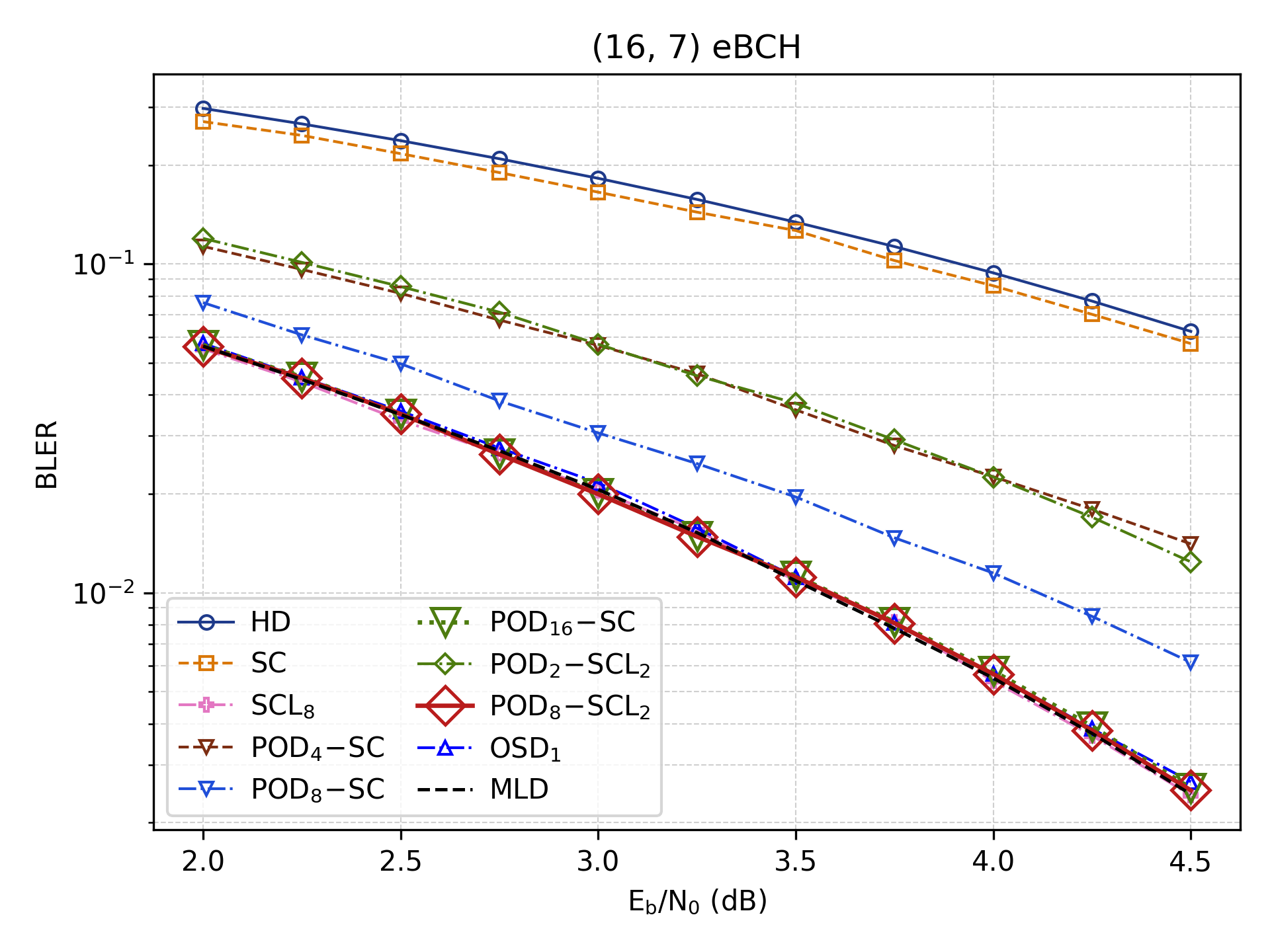
The Polar Orbit Decoding (POD) framework establishes a remarkably unified approach to error correction, achieving decoding performance nearing the theoretical maximum likelihood (ML) benchmark while significantly reducing latency. Demonstrated with a (16,7) extended BCH code utilizing just 16 permutations, POD attains comparable results to Successive Cancellation List (SCL) decoding – a traditionally robust, yet computationally intensive, method. Notably, POD achieves this level of performance with an effective list size equivalent to an SCL decoder requiring a list size of 8, representing a substantial gain in efficiency. This parity in performance, coupled with the potential for flexible resource allocation, positions POD as a compelling alternative for applications demanding both high reliability and real-time performance.

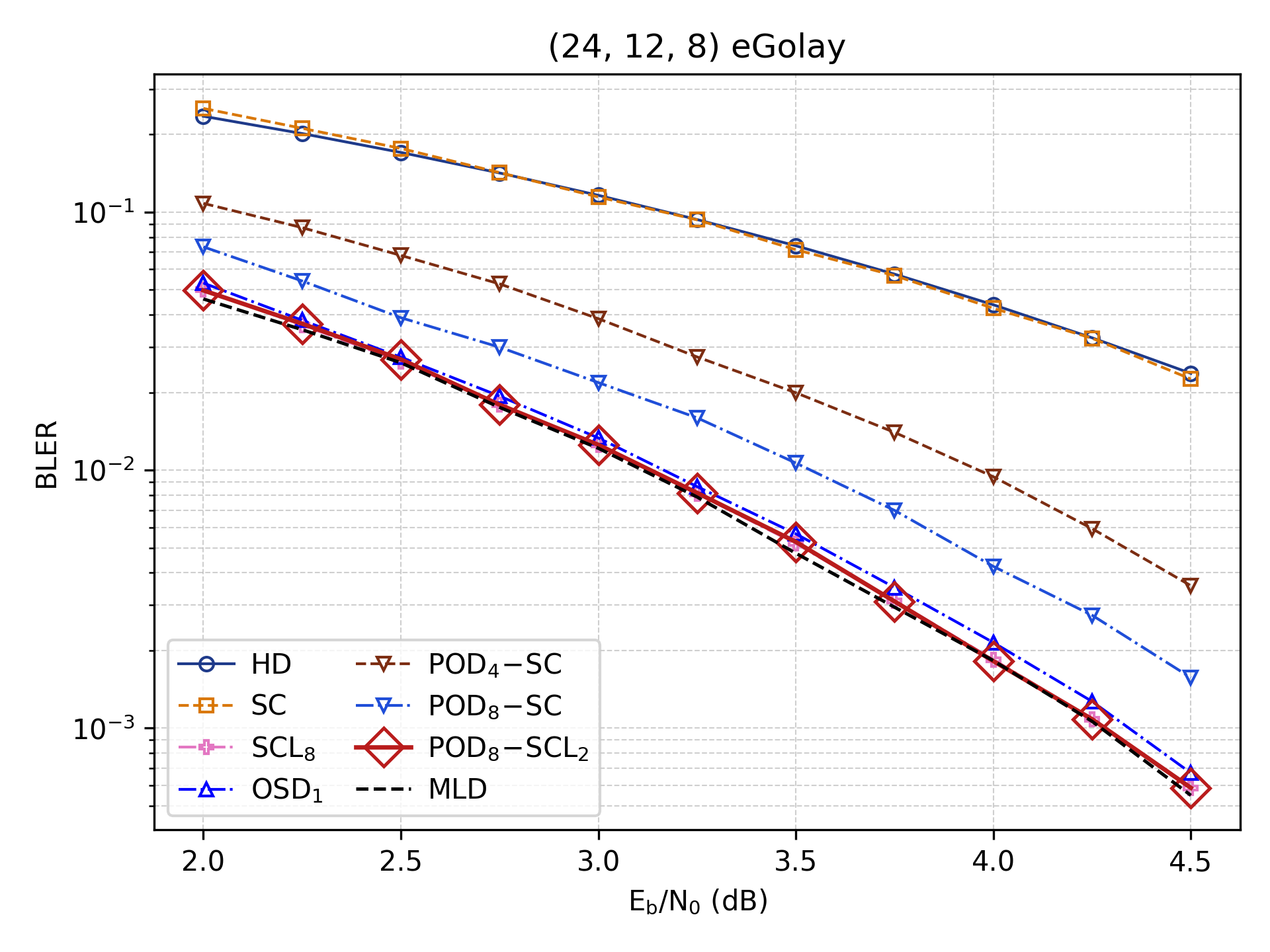
The exceptional symmetry inherent in certain error-correcting codes is powerfully exploited by the Polar Orbit Decoding (POD) framework, as exemplified by Extended Golay codes which possess an automorphism group order of 244,823,040. This immense symmetry – representing the number of self-mappings that preserve the code’s structure – allows POD to decompose the decoding process into a multitude of independent, parallel operations. Rather than treating decoding as a sequential task, the framework leverages these symmetries to explore a vast solution space concurrently, significantly reducing latency. This capability isn’t limited to Golay codes; similar symmetries exist within other codes like Extended BCH, offering a unified and efficient approach to near-maximum likelihood decoding through parallel processing.

Polar Orbit Decoding (POD) presents a compelling trade-off between computational demands and decoding performance, achieving results on par with Successive Cancellation List (SCL) decoding but with enhanced flexibility. Utilizing M permutations within the POD framework delivers performance equivalent to SCL employing a list size of M*L, where L represents a conventional list size parameter. This scalability is crucial; by adjusting M, the degree of parallelism can be tuned to optimally utilize available hardware resources, allowing for a reduction in decoding latency. Consequently, POD offers a practical solution for applications demanding both high reliability and real-time performance, providing a means to balance computational cost with the desired level of error correction capability.

The <span class="katex-eq" data-katex-display="false"> (24, 12) </span> eGolay code demonstrates strong performance characteristics. — The $(24, 12)$ eGolay code demonstrates strong performance characteristics.

The pursuit of efficient decoding, as evidenced in this work on Polar Orbit Decoding, often feels less like construction and more like tending a garden. The method’s reliance on automorphism groups to unlock parallelism isn’t about building a faster decoder, but rather about discovering inherent symmetries within the code itself – coaxing performance from the structure already present. As Linus Torvalds once stated, “Talk is cheap. Show me the code.” This sentiment rings true; the elegance of POD lies not in theoretical complexity, but in its practical demonstration of how to leverage mathematical foundations for tangible gains in decoding latency. Every architectural choice, however, remains a prophecy; even optimized parallel decoding anticipates the inevitable arrival of longer codes and increasingly demanding performance requirements.

The Looming Horizon

The pursuit of universal decoding, as exemplified by Polar Orbit Decoding, invariably reveals the shifting sands beneath any claim of architectural permanence. This work, while promising gains in parallelization, merely refines the interface between order and inevitable chaos. Every attempt to extract maximum performance from a code’s symmetries introduces new dependencies, new points of failure obscured by layers of abstraction. The automorphism group, so neatly leveraged here, will, in time, become a bottleneck, a new master to serve.

The real challenge isn’t achieving faster decoding – it’s accepting that latency will always be a tax on complexity. The focus will not remain on the codes themselves, but on the dynamic management of frozen constraints – the art of controlled entropy. Future work will likely explore adaptive techniques, where the very structure of the code morphs in response to channel conditions – a self-healing system, perpetually reconstructing itself from the wreckage of past errors.

Ultimately, this research, like all such endeavors, doesn’t solve the problem of communication – it merely postpones it. The true horizon lies not in better algorithms, but in a deeper understanding of the fundamental limits of information, and the graceful acceptance of imperfection.

Original article: https://arxiv.org/pdf/2601.11373.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

The Fragile Foundation of Reliable Transmission

Polar Codes: Approaching the Limits of Communication

Decoding Through Symmetry: Leveraging Automorphism Groups

Decoding as Permutation: A Unified Approach with Polar Orbit Decoding

The Looming Horizon

See also: